Mathcad программалау ортасы және көп айнымалы функцияларды аналитикалық-сандық есептеу әдістері


Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 30 бет
Таңдаулыға:
1. 3 Mathcad программалау ортасы
Компьютерлік математика - ғылымы мен техникадағы жаңа бағыт . Ол кластикалық математика мен информатиканың тиісумен туындайды. Компьютерлік математиканың маңыздылығы оның прогрммалық жүйемен қамтамасыз етілуінде және кез-келген математикалық есептерді шешу қабілетінде . Компьютерлік математика жүйесі батыстың mathsost, Mathwors, Maple, Wolsrom сукілді фирмаларда жасалған. Mathcad ғылыммен білімніңң және техниканың әр түрлі аймақтарын автоматтандыру үшін математикалық есептеулеге арналған. Жүйенің аталуы екі сөзден құралған, яғни MATHematica ( математика) және САД (Computer Aided Desing -автоматты жобалау жүйесі немесе АЖЖ ) . Сондықтан MATHCAD-ты математикалық автоматты жобалау жүйесі деп аталады.
2. MATHCAD-тың көмегімен кітап, диссертация, ғылыми есеп дипломдық және курстық жобаларды тек әртүрлі үлгідегі сапалы мәтін мен ғана емес, ең күрделі математикалық формула жиынтығымен, есептеулермен, графиктік көрністермен дайындауға болады. MATHCAD программаның мұндай мүмкіндіктері электрондық сабақтар, лекциялар курсы, электронды кітаптар жазуда маңызы жабдыққа айналып отыр. сонымен бірге компьютерлік математика жүйесі көркем өнер, графика, линвистика саласында кеңінен қолданыс табылды. MATHCAD-тың жаңа нұсқасында құжаттардың көркем түсті эффектілі құрылғы және графикті аниммациялану, дыбысты қосып шығару мүмкінділігі қосылған. Осы артықшылықтарына байланысты мәтіндік, формулалық және графиктік редакторлар қуатты есептеуіш потенциялды орта жүйесімен беріледі. Өте күрделі тапсырмаларды шешу үшін математикалық және графикалық жүйелер және олардың біргуі қарастырылатын. Бұл жүйе әртүрлі математикалық, графикалық және офистік жүйе қатарымен кеңитетін интегралды қамтамасыз етеді. MATHCAD-ты тек қана математикалық есептерде үшін емес басқада қуатты инженерлік автоматтандырылатын жобалау жүйесін дайындаумен бірге, графиктерді
MATHCAD жүйесінің файлдары . mcd кеңейтілуіне ие болады. Мұндай файлдар текстік форматта болады, сондықтан оларды кез келген текстік редакторда оқуға болады. MATHCAD файлдарының құжатында программаның толық тексті болады.
File менюінің ішкі менюі.
New - жаңа құжат құру.
Open - дайын құжатты ашу.
Close - құжатты жабу.
Save - құжатты сақтау.
Save as… - жаңа атпен сақтау.
Colloborabory - жүйені құрушы фирмамен байланыс орнату.
Internet Setup - Internet -пен модем арқылы байланыс.
Send… - электрондық почтамен немесе Internet-пен құжатты жіберу.
Page Setup… - бетте оң және сол шегіністерді орнату.
Print Preview - баспаға шығарда алдын -ала қарау.
Print - құжатты шығару.
Exit - жүйеден шығу.
MATHCAD жүйесінің жаңа версиясында мүмкіндік ол - телекоммуникация құрылғыларымен тығыз байланысты. Осылайша қиын документтермен, проектілермен организациялар үшін бірігіп жұмыс істеу мүмкіндіктері пайда болды. Мұндай байланысты орнату үшін File менюіндегі Collaborato-ry… командасын пайдаланамыз. Құжатты баспаға шығару - жүйесінің басты мүмкіндігі .
Page Setup… командасы баспаға шығатын беттердің параметрлерін орнатады.
Print… командасы құжатты баспаға шығарады. Бұл команданы орындағанда экранда диалогтық терезе пайда болады.
Баспаға шығару терезесі арқылы принтер параметрлерін орната аламыз. Windows операциялық жүйесі бірнеше типтегі принтерлер арқылы баспаға шығаруды ұсынады. Диалогтық терезеде құжат беттерінің диапазоны көрсетіледі.
MATHCAD жүйесінің құжаттары екі еселік ұзындықта және ендікте. Алдымен сол бөліктің баспасы шығады, содан соң оң жақтың баспасы шығады. Екеуін клейлеп құжаттың толық мазмұнын алады.
Редакциялау процесінің үлкен бөлігі объектілер бейнеленген ағымдық терезеде орындалады. Редакциялауды ағымдық терезеге бір немесе бірқатар шаблондар объектісін ендірген соң бастай аламыз. Объектілерді ендіру жолдары әр түрлі. Мысалы х=1 айнымалысына мән беріп sin(x) мәнін есептеу үшін клавиатурадан ендіруді қолдануға болады.
Х айнымалы атын ендіру.
Х:= меншіктеу символын ендіру.
Х:=1 1 сандық константасын ендіру.
Enter
Sin sin функциясын ендіру.
Sin ( сол жақ жақшаны ендіру.
Sin (x х айнымалы атын ендіру.
Sin (x) оң жақ жақшаны ендіру.
= теңдік белгісін ендіру.
Enter sin (x) = sin (1) мәнін есептеу.
0, 841
Формулалық редакторды қосу үшін редакциялау процесінің кез келген аймағында тышқанның сол жақ бөлігін басу керек. Кішкене қызыл кресть түрінде визир пайда болады. Оны курсормен ары - бері жылжытуға болады. Вирзерді тышқан курсорымен шатастырмау керек. Визер формулаларды теруді қайданбастаау керектігін көрсетеді. Жүйенің негізгі менюқұрамы:
File ( файл ) - файлдармен жұмыс.
Edit ( правка ) - құжаттарды редакциялау
Viev ( обзор) - шолу құрылымын өзгерту.
Inseret ( вставка) - обьектілермен шаблондарды қою
Format ( формат) - обьектілер форматынт өзгерту
Math ( математика) - есептеу процесін басқару
Graphics (графика) - графикалық редактормен жұмыс
Symbolic ( символика) - символдық процессордың операцияларын таңдау
Window ( Окно ) - жүйенің терезелерін басқару
Books (книги) - электронды кітаптармен жұмыс
Help ( ?) - жүйе туралы анықтамалықпен жұмыс
Есептеу операторлары
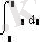
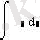
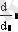
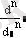
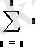
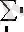
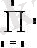
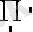
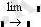
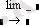
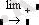
Math CAD бағдарламасының көмегімен аналитикалық есептеу негіздерін, туынды, интеграл және де алгебралық теңдеулерді шешу мүмкіндігін қарастырады. Осы операцияларды орныдау Symbolics (Символика) менюінде орындалады. Ол Variable (Переменная) менюнде орналасқан.
Есептеу операторы
Есептеу операторы құрал саймандар тақтасындағы
Calculus
(Вычисления) командасымен орындалады. Кез келген пернені басқанда математикалық нәтиже шықатын символ тізбегі шығады.
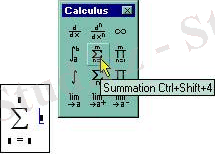
Сур. 3. 7.
Қосынды операторының жазылуы
Негізігі есептеу операторын және оларға қарапайым мысалдар келтірейік:
- дифференциалдау және интегралдау;
туынды (листинг 3. 20) ;
N-ші туынды (листинг 3. 20) ;
анықталған интеграл (листинг 3. 21) ;
анықталмаған интеграл (листинг 3. 21) .
- қосынды және туындыны есептеу ;
қосынды (листинг 3. 22) ;
туынды (листинг 3. 22) ;
ранжілі қосындының шегі (листинг 3. 23) ;
ранжілі туындының шегі (листинг 3. 23) .
- шек (листинг 3. 24) ;
екіжақта ;
сол;
оң.
Листинг 3. 20. Туындыны есептеу операторы

Листинг 3. 21. Интегралдық оператор

Листинг 3. 22. Туындыны және қосындыны есептеу операторы

Листинг 3. 23. Ранжлі шекті қосындыны және туындыны есептеу операторы

Листинг 3. 24. Шекті символды есептеу операторы
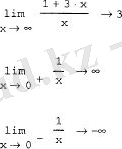
Дифференциалдау. (Differentiate)
Аналитикалық дифференциалды теңдеуді шешу үшін келесі команда орныдалады:
Symbolics / Variable /Differentiate
(Символика/Переменная/Дифференцировать)
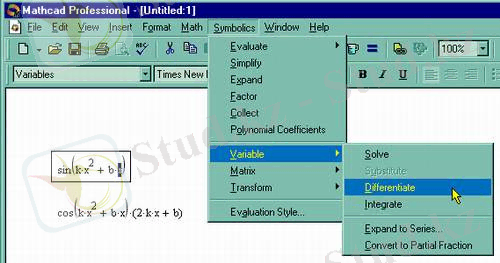
Рис. 5. 13.
Дифференцирование по переменной
Интегралдау (Integrate)
Анықталмаған интегралды есептеу үшін қандай да бір
Symbolics / Variable / Integrate
(Символика / Переменная / Интегрировать) командасын орындау қажет.
Аналитикалық анықталмаған интегралды есептеу кейіннен пайда болады. Осының нәтижесінде MathCAD - да функция пайда болады.
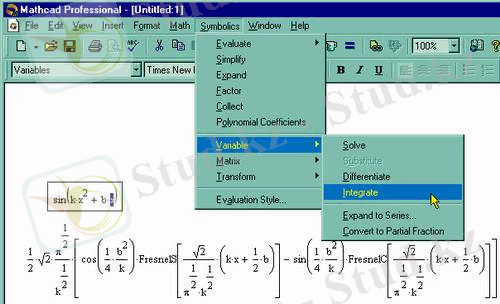
Рис. 5. 14.
Интегрирование по переменной
MathCAD - интегралдау түрі есептеу операторымен жүзеге асады.
Допускается вычислять интегралы от скалярных функций в пределах интегрирования, которые также должны быть скалярами. Несмотря на то, что пределы интегрирования обязаны быть действительными, подынтегральная функция может иметь и комплексные значения, поэтому и значение интеграла может быть комплексным. Если пределы интегрирования имеют размерность
(см. разд. "Размерные переменные" гл. 4),
то она должна быть одной и той же для обоих пределов.
Интегралдау операторы.
MathCAD - та интгралдау, дифференциалдаудың математикалық нәтижесі қалаай жазылса, солай орындалады. Анықталған интгерлды есептеу үшін
Calculus
(Вычисления) командасын немесе <Shift>+<7> пернесі арқылы орындалады, ("&" символы арқылы) .
Толтырылатын ұяшықтар бойынша интеграл символы пайда болады.
Можно вычислять интегралы с одним или обоими бесконечными пределами. Ол үшін орнына шектің символын қоямыз, мысалы,
Calculus
(Вычисления
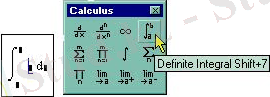
Сур. 7. 1.
Интегралдық оператор
Интгралдың нәтижесін алу үшін теңсіздік белгісін немесе символдық теңсіздік белгісін қоямыз. MathCAD символдық процессорының көмегімен толық нәтижесі, екіншіден сандық түрі көрсетіледі. Төмендегі листнигте көрсетілген
Листинг 7. 1. Анықталған интгералдың сандық және символдық көрсетілімі
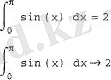
Листинг 7. 2. Интегрирование функции двух переменных по разным переменным

Листинг 7. 3. Функцияда интегралдық оператордың қолданылуы

Листинг 7. 5. Шекті интегралдың символдық есептелуі
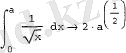
Листинг 7. 6. Анықталмаған интегралдың символдық есептелуі
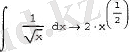
Еселі интеграл
Еселі интегралды есептеу үшін:
1. Қарапайым түрдегі операторлық интегралды есептеу керек .
2. Бірінші шектің орнына тиісті шекті интегралды орнына қоямыз.
3. Операторлық интегралдың орнына тағы бір интегралдық функцияны қоямыз.
4. Тағы осындай етіп екінші шекті интгралды орындаймыз .
Төменде символдық және сандық екі еселі интегралдың мысалы көрсетілген.
Листинг 7. 8. Символдық және сандық еселі интегралдың есептелу
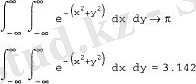
Листинг 7. 9. Символдық еселі интегралды есептеу

Дифференциалдау
MathCAD көмегімен кез келген туындыны есептеуге болады. Функция және аргумент анық, сондай-ақ комплексті болуы мүмкін. MathCAD - та дифференциалды есептеу процесі дәл, тура есептеуді қамтамасыз етеді. Көбінесе қолданушы символдық процессорды, туынды функциясын топтастырып есептеп жүзеге асырады.
Бірінші ретті туынды.
f (х) функциясын кез келген нүктеде дифференциалдау үшін:
1. Туынды есептелетін х нүктесін анықтау қажет, мысалы, х:=1
2. Дифференциалды операторды енгізіп, Calculus (Вычисления) панелінде Derivative ( Производная) командасын басу керек немесе пернетақта көмегімен <?> белгісін енгіземіз. 3. Пайда болған толтыру орнына функцияны, х аргумент f (х) орналастырамыз4. Нәтижесін алу үшін <=> операторын немесе <- символын енгізу керек.
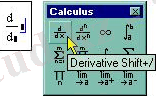
Рис. 7. 3.
Дифференциалдық оператор.
f (x) =cos(x) -sin(x) дифференциядық функцияның мысалы 7. 10. листинге көрсетілген
Листинг 7. 10. Сандық және символдық дифференциалдау.
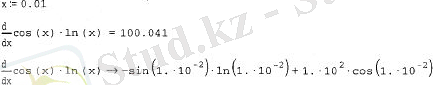
Листинг 7. 11. Символдық және сандық дифференциалды қолдану

Листинг 7. 12. Операторлық дифференциалды функция арқылы анықтау
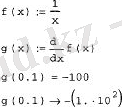
MathCAD процессорының көмегімен туынды функциясының аргументін есептеуге де болады. Бұл жағдайда, бізге белгілі түрлі аргументті туынды дербес деп аталады.
Дербес туындыны есептеу үшін,
Calculus
(Вычисления) панеліне туынды операторын енгіземіз, тиісті орынға дифференциалға тиісті шекті қоямыз.
Төменде мысал келтірілген, бірінші қатарда екі еселі шек анықталған, екінші қатарда дербес туындының х, у қатысты есептеу көрсетілген.
Листинг 7. 16. Дербес туындының сандық және символдық есептелуі

Дербес туындының жоғарғы қатары, жай туынды секілді есептеледі.
Листинг 7. 17. Екі еселі дербес туындының есептелуі
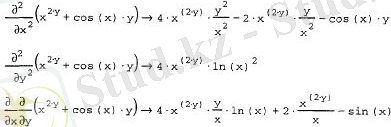
Жоғарыда көрсетілген мысалдарда, дифференциалдық оператор дербес туынды түрінде көрсетілген. Дифференциалды оператордың түрін дербес туындыға өзгерту үшін:
- Дифференциалды оператордан констекті мәзірін тышқанның оң жақ батырмасын басу арқылы орындаймыз.
- Констекті мәзіріненView DerivativeAs (Показывать производную как) пунктін таңдаймыз.
- Пайда болған мәзірденPartial Derivative(Частная производная) пунктін аламыз.
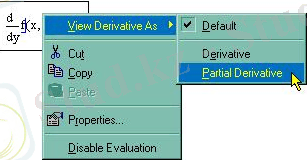
Рис. 7. 5. Дифференциалды оператордың өзгертілуі
Теңдеуді шешу. (Solve)
Символдық процессордың көмегімен шекті аналитикалық мағынасы бар теңдеуді шешуге болады. Ол үшін
1. Теңдеуді енгіземіз.
2. Теңдеу шешетін шекті белгілейміз.
3. Мәзір қатарынан Symbolics (Символика), Variable / Solve (Переменная / Решить) пунктін таңдаймыз. Төмендегі суретте көрсетілген.
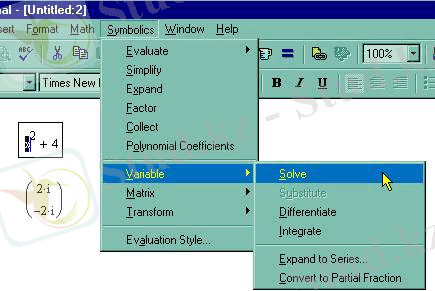
Рис. 5. 19.
Символдық теңдеуді шешу
2 . КӨП АЙНЫМАЛЫ ФУНКЦИЯЛАР ЖӘНЕ ОЛАРМЕН ЖҰМЫС ІСТЕУ ҮШІН КОМПЬЮТЕРДІ ҚОЛДАНУ
2. 1. Анықтамалар, ұғымдар
Анықтама. Егер х; у тәуелсіз айнымаларының қос мәндерінде z-тің анықталған бір мәні сәйкес келсе, онда z-і х, у айнымалыларының функциясы деп атайды
Анықтама. Функция анықталатын және бар болатын х және у аргументтерінің мәндерін екі айнымалы функцияның анықталу облыс деп атайды және D мен белгілейді.
Екі айнымалы функцияның анықталу облысы үшін х Оу жазықтығының бөлігі алынады. Жазықтықтың бөлігін шектеп тұрған сызық облыстың шекарасы деп аталады. Тек ішкі нүктелерден тұратын облыс ашық облыс деп аталады. Егер облыста шекара нүктелері кіретін болса, онда ол тұйық облыс деп аталады.
Анықтама. Егер тәуелсіз
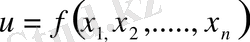
u функциясы анықталатын
Мысалы:
Түбір астындағы өрнек теріс болмау керек:
Екі айнымалы функцияның геометриялық кескіні
D облысында х ; у екі айнымалы функция берілсін делік.
Функцияны кескіндейміз. Әр
Нүктелері сәйкес келеді. Аналитикалық геометриялық орны бетті беретіні белгілі. Ендеше екі айнымалы z = f (x, y) беттің теңдеуін береді.
Үш және одан көп айнымалылы функциялардың геометриялық бейнесін беру мүмкін емес.
Мысал. Екі айнымалылы функциясының бейнесін беру керек:
Екі айнымалы функциялардың шегі мен үзіліссіздігі
Анықтама.
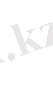
Анықтама. Егер
саны үшін
әрі х; у-тер
Анықтама. Егер
теңдігі орындалатын болса, онда f (x; y) функциясы осы нүктеде үзіліссіз деп аталады.
Анықтама. Егер функция облыстың әрбір нүктесінде үзіліссіз болса, онда функция облыста үзіліссіз деп аталады.
өйткені
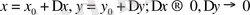
онда
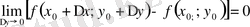
немесе
Үзіліссіздіктің басқа анықтамасын береміз.
Анықтама. Егер
Анықтама. Мына жағдайларда үзіліс нүктесі болады:
1. f (x; y) функциясы нүктесінде анықталмаған.
2. f (x; y) функциясы нүктенің өзінде және маңайында анықталған, ал шегі жоқ. .
3. Функцияның шегі бар, нүктеде және оның маңайнда анықталған, бірақ
2. 3. ТУЫНДЫЛАР ЖӘНЕ ОЛАРДЫ КОМПЬЮТЕРДЕ ЕСЕПТЕУ
Функцияның туындысы
 онда функция да өсімше алады:
онда функция да өсімше алады:
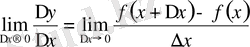 қатынасының шегін қарастырамыз.
қатынасының шегін қарастырамыз.
Анықтама. Функция өсімшесінің аргумент өсімшесіне қатынасының аргумент өсімшесі нөлге ұмытылғандығы шегі функцияның туындысы деп аталады және былай белгіленеді:
Функцияның дифференциалдануы. 1- анықтама. Берілген функциядан туынды табу амалы функцияны дифференциалдау деп аталады.
2 - анықтама. Егер
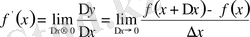 туындысы бар болса, онда
туындысы бар болса, онда
Егер
Күрделі функцияның туындысы.
Күрделі функция тізбек түрінде екі тізбекпен берілсін:
Теорема. Егер
Мысал:
Күрделі функцияны элементар функциялардың тізбегі түрінде жазамыз:
() формула бойынша табамыз
Ескі айнымалыға көшеміз:
Жоғары ретті туындылар
Дифференциалданатын
Анықтама. Функцияның туындысынан алынған туынды екінші туынды деп аталады. Функцияның екінші туындысынан алынған туынды үшінші туынды немесе үшінші ретті туынды деп аталады және т. с. с. оларды былай белгілейді:
және т. б.
Мысалы: 1.
2.
Көп айнымалы функциялардың дербес туындылары
D облысында
Анықтама.
Екі айнымалы функцияның дербес өсімшесінің сәйке аргументінің нөлге ұмытылатын өсімшесіне қатынасының шегі дербес туындысы деп аталады және былай белгіленеді:
Басқа дербес туындыларда осылай анықталады:
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz