Жалпы салыстырмалы теориядағы екі айналмалы дене есебі: Фоктың бірінші жуықтау метрикасы, қозғалыс теңдеулері және орнықтылық


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 32 бет
Таңдаулыға:
ӘЛ-ФАРАБИ АТЫНДАҒЫ ҚАЗАҚ ҰЛТТЫҚ УНИВЕРСИТЕТІ
Физика факультеті
Теориялық физика кафедрасы
Диплом (Бітіру) жұмысы
Жалпы салыстырмалы теориядағы екі айналмалы дене есебі
Орындаушы:
4 курс студенті - - - - - Құдайбергенова А. Т
Ғылыми жетекші:
ТФК меңгерушісі,
физ-мат. ғыл. к., доцент - - - - - - Әбішев М. Е.
(қолы, мерзімі)
Норма бақылаушы: __ __ __ __ __ __ __ __ __ __ __ __ __ Белисарова Ф. Б.
физ-мат. ғыл. к., доцент ( қолы, мерзімі )
Қорғауға жіберілді:
ТФК меңгерушісі,
физ-мат. ғыл. к., доцент - - - - - - Әбішев М. Е.
( қолы, мерзімі)
Алматы 2009
Реферат
« ЖСТ- дағы екі айналмалы дене есебі» тақырыбында жазылған дипломдық жұмыс кіріспе, екі негізгі тараудан, алты параграфтан, қорытынды бөлімінен және пайдаланылған әдебиеттер тізімінен тұрады. Жұмыс барысында тартылыс теориясы, орталық өріс, сыналатын дене, төрт өлшемді кеңістік-уақыт, импульс моменті, Лагранж функция, орбиталды орнықты сияқты физикалық түйін сөздер қолданылған.
Жұмыс құрылымы негізі 32 беттен, кіріспеден, екі тараудан, қорытынды және қолданылған әдебиеттер тізімінен тұрады.
Зерттеу обьектісі: ЖСТ-дағы соңғы ғылыми ашуларды, сонымен қатар Фоктың бірінші жуықтау метрикасын, лагранж функциясын, екі дене есебінің қозғалыс теңдеуін және айналмалы денелер есебінің тұрақтылығын зерттейді.
Жұмыстың мақсаты: ЖСТ-дағы екі айналмалы дене есебінің қозғалыс теңдеуін шешу.
Белгілеулер мен қысқартылған сөздер
ЖСТ - жалпы салыстырмалы теория
АСТ - арнайы салыстырмалы теория
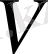 -
жылдамдық;
-
жылдамдық;
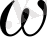 - үдеу;
- үдеу;
 - Гамильтон функциясы;
- Гамильтон функциясы;
L- Лагранж функциясы;
 - баяулау параметрі;
- баяулау параметрі;
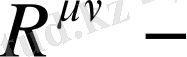 Риччи тензоры;
Риччи тензоры;
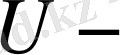 Ньютон потенциалы;
Ньютон потенциалы;
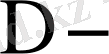 Лаплас операторы;
Лаплас операторы;
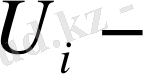 тартылыс вектор-потенциал;
тартылыс вектор-потенциал;
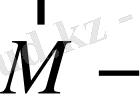 импульс моменті;
импульс моменті;
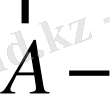 Лаплас векторы;
Лаплас векторы;
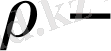 масса тығыздығы;
масса тығыздығы;
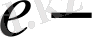 ексцентриситет;
ексцентриситет;
МАЗМҰНЫ
КІРІСПЕ . . . 3
1. Бөлім. ЖСТ-дағы денелер механикасының бірінші жуықтау метрикасы
1. 1 Фоктың бірінші жуықтауының нақтыланған метрикасы… . . . 4
1. 2 Орталық өрістегі қозғалыс жайлы есеп . . .
2. Бөлім. Ішкі құрылымы мен өздік айналысын ескергендегі
екі дене есебі
2. 1 Лагранж функциясы және қозғалыс теңдеуі . . . ……… . . .
2. 2 Бірінші жуықтау теңдеуін зерттеу . . .
2. 3 Екі айналмалы дене есебінің өздік айналысы . . .
2. 4 Екі айналмалы дене есебінің орбиталдық және орбитаның векторлық элементтеріне қатысты орнықтылығы . . .
ҚОРЫТЫНДЫ . . . 25
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . . 26
Кіріспе
«Салыстырмлық теория» атауы жаңа кеңістік пен уақыт теориясын жасаған Пуанкаре мен Эйнштейннің негізгі принцип (постулатынан) шыққан.
Салыстырмалық теорияның мәні кеңістік пен уақыттың, екеуінің арасындағы геометриялық сипаттағы байланысын ескеретін физикалық теория.
Жалпы салыстырмалық теория (ЖСТ) - қазіргі заманғы тартылыс теориясы. Бұл теорияда төрт өлшемді кеңістік уақыт қисығымен байланыстырады.
Тартылыс теориясының классикалық вариантын XVII ғ. Ньютон қалаған. Ол көптеген қазіргі заманғы астрономия, астрофизика, космонавтика есептеріне жарады. Классикалық тартылыс заңында бір кемшілік болды, ол алыстан әсер ету теориясы. Онда бір дененің екінші денеге гравитациялық әсері лезде, кешікпей беріледі. Бірақ лездік әсер табиғатта жоқ. Шындығында, егер бірінші денеде бір өзгеріс болса, онда екінші денеде сол өзгеріс біраз уақыт өткеннен кейін болуы керек, сондықтан гравитацияда алыстан әсер етуден құтылу керек болды, оны жасаған Эйнштейн. Негізі тартылыс теориясы, яғни ЖСТ бір адамның талпынысымен құрылған теория. 1905ж. «К электодинмике движущихся сред » деп аталатын Эйнштейннің арнайы салыстырмалы теориясы (АСТ) мен классикалық электродинамикаға арналған жұмысы аяқталған түрінде шыққан болса, ЖСТ құруға ұзақ уақыты кетеді. Ол 1907 ж. осы жұмысты бастайды, ал соңы тек 1915ж. 18-25 қарашада Берлинде өткен Пруссиялық ғылым Академиясының отырысында баяндалды.
ЖСТ-физикалық теория, негізінде эксперименттермен дәлелденген нақты принцип жатыр.
ЖСТ-ң маңызды мәселелерінің бірі- денелер қозғаласы мәселесі.
Қазіргі кезде ЖСТ релятивтік аспан механикасының теориялық негізі ғана емес, сонымен қатар аспан денелерінің қозғалысын есептеуде көп қолданылады. Ал ол есептеулер өз кезегінде астрономиялық өлшемдер нақты табуға мүмкіндік береді.
Дипломдық жұмыстың құрамы кіріспеден, екі тараудан, қорытынды, пайдаланылған әдебиеттер тізімінен тұрады. Бірінші тарауда Фоктың бірінші жуықтау метрикасы есептеліп, нақтыланса, ал екінші тарауда екі айналмалы дененің ішкі құрылымын және өзіндік айналымын есептеуге бағытталған.
1. Бөлім. ЖСТ-дағы денелер механикасының бірінші жуықтау метрикасы
1. 1 Фок бірінші жуықтауының нақтыланған метрикасы
Қозғалыс теңдеуін бірінші жуықтау метрикасынан бастаған ыңғайлы. Ондай метриканы Фок өзінің монографиясында /1/ көрсеткен. Ол Эйнштейн теңдеуінен бастайды
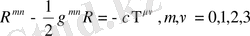 (1. 1)
(1. 1)
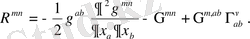 Equation. 3 (1. 2)
Equation. 3 (1. 2)
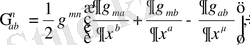 (1. 3)
(1. 3)
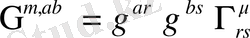 Equation. 3 (1. 4)
Equation. 3 (1. 4)
бір
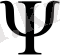 функциясынан алынған Даламбер операторының түрі:
функциясынан алынған Даламбер операторының түрі:
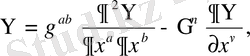 (1. 5)
(1. 5)
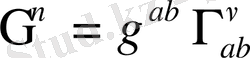 (1. 6)
(1. 6)
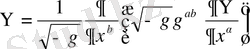 (1. 7)
(1. 7)
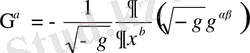 (1. 8)
(1. 8)
сонымен қатар
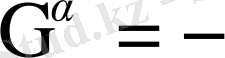
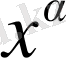 (1. 9)
(1. 9)
 (1. 10)
(1. 10)
немесе
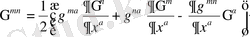 (1. 11)
(1. 11)
 Equation. 3 вектор болмаған соң,
Equation. 3 вектор болмаған соң,
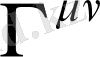 тензор емес. Осы жағдайды қолданып, Эйнштейн теңдеуін қарапайым түрге келтіруге болады.
тензор емес. Осы жағдайды қолданып, Эйнштейн теңдеуін қарапайым түрге келтіруге болады.
Эйнштейн теңдеуі жалпыковарианты болғандықтан, төрт тәуелсіз функциядан тұратын координат түрлендіруге болады.
Бірінші жуықтау метрикасы массаның аралдық үлестірілу сипатынан шығарады. Ол шекті шартты шексіздік етіп қоюға мүмкіндік береді, ал ол өз кезегінде есепті математикалық анық етеді.
Массаның аралдық үлестіруінде шексіздіктегі тартылыс өрісі нөлге ұмтылады. Сондықтан массадан үлкен қашықтықтарда кеңістік-уақыт геометриясы псевдоевклидті болады. Геометрия псевдоевклидті болғанда, галилей координаты x, y, z, t орынды, ал интервал квадратының түрі:
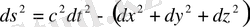 (1. 12)
(1. 12)
Ньютон теориясы галилей координаталарына (инерциалды санақ жүйесінде) қарапайым жазылады. Ньютон теориясы релятивисттік емес теория. Релятивистік емес теориясынан релятивистік көшу үшін үлкен параметр жарық жылдамдығын
 таңдап аламыз.
таңдап аламыз.
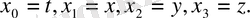 (1. 13)
(1. 13)
- өрнегінен интервал квадраты былай жазылады:
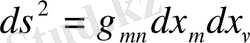 (1. 15)
(1. 15)
шексіздіктегі
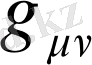 -нің келесі шекті мәні:
-нің келесі шекті мәні:
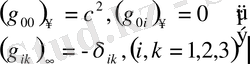 (1. 16)
(1. 16)
Метрикалық тензордың контровариантты компоненттері үшін шекті мәндері:
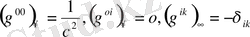 (1. 17)
(1. 17)
Осы формулаларды метрикалық тензордың шекті шарттары ретінде қарастыруға болады.
Эйнштейн теңдеуі толқындық түрдегі теңдеу, оның басты мүшелері Даламбер операторының түріне ие. Массадан тыс
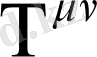 тензор нөлге тең және теңдеу мына түрге келеді:
тензор нөлге тең және теңдеу мына түрге келеді:
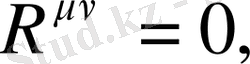 (1. 18)
(1. 18)
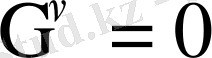 шарты орындалса
шарты орындалса
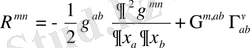 (1. 19)
(1. 19)
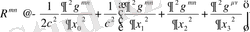 (1. 20)
(1. 20)
Эйнштейн тартылыс теориясын Ньютон теориясымен салыстыру үшін Эйнштейн тартылыс теңдеуіне кіретін
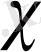 тұрақтысын анықтау керек
тұрақтысын анықтау керек
 (1. 21)
(1. 21)
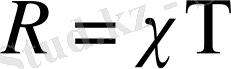 (1. 22)
(1. 22)
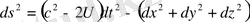 (1. 23)
(1. 23)
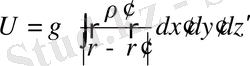 (1. 24)
(1. 24)
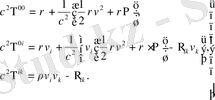 (1. 25)
(1. 25)
Тартылыс өрісі болғандағы серпімді дене массасының тензоры:
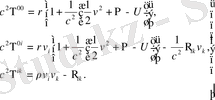 (1. 26)
(1. 26)
тығыздық мен энергия ағынына сәйкес келетін мүшелерін алып тастасақ
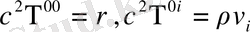 (1. 27)
(1. 27)

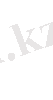 (1. 28)
(1. 28)
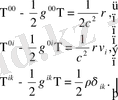 (1. 29)
(1. 29)
гармониялық координат жүйесінде (1. 20) өрнегі
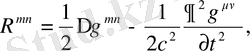 (1. 30)
(1. 30)
(1. 30) мен (1. 29) өрнекткрін (1. 21) қойсақ
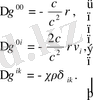 (1. 31)
(1. 31)
(1. 23) өрнекке сәйкес
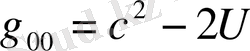 (1. 32)
(1. 32)
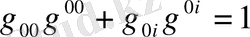 (1. 33)
(1. 33)
формуласына қолданады.
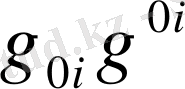 мүшесін өте аз шама екенін ескеріп, формуланы былай жазады
мүшесін өте аз шама екенін ескеріп, формуланы былай жазады
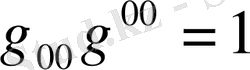 (1. 34)
(1. 34)
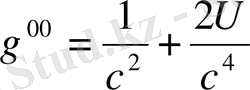 (1. 35)
(1. 35)
ньютон потенциалы мына формуланы қанағаттандырады
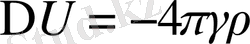 (1. 36)
(1. 36)
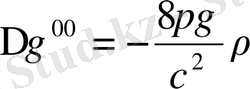 (1. 37)
(1. 37)
(1. 31) өрнегін (1. 37) өрнегімен салыстырып
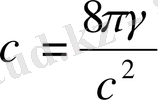 (1. 38)
(1. 38)
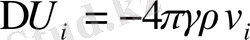 (1. 39)
(1. 39)
жоғарыдағы формуланы қанағаттандыратын функция енгіземіз
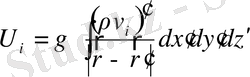 (1. 40)
(1. 40)
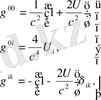 (1. 41)
(1. 41)
Метрикалық тензордың контраварианттық компонентінен алгебралық жолмен коварианттық компонентін және де басқа шамаларын таба аламыз.
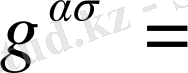
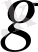 анықтауышының
анықтауышының
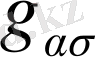 элементтінің алгебралық толықтауышы/
элементтінің алгебралық толықтауышы/
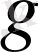
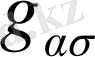 элементтінің алгебралық толықтауышы=
элементтінің алгебралық толықтауышы=
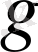 анықтауышының
анықтауышының
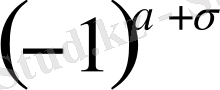
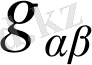 элементінің миноры
элементінің миноры
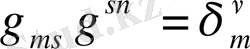 (1. 42)
(1. 42)
Егер
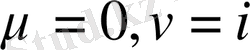 , онда
, онда
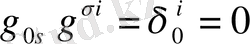 (1. 43)
(1. 43)
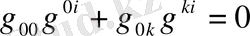 (1. 44)
(1. 44)
немесе
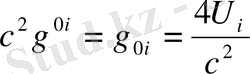 (1. 45)
(1. 45)
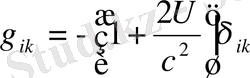 (1. 46)
(1. 46)
Сонымен, Фок бойынша бірінші жуықтау метрикасы /1, c. 271/ мынада түрге ие:
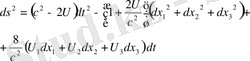 (1. 47)
(1. 47)
Осы метрикаға қатысты келесі ескертулер шығады:
1.
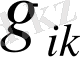 және
және
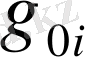 компонентінде болатын релятивистік қосымша метрикалық тензордың
компонентінде болатын релятивистік қосымша метрикалық тензордың
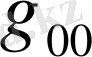 компонентінде жоқ. Ол Фок бір уақытта екі есепті:
компонентінде жоқ. Ол Фок бір уақытта екі есепті:
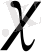 тұрақтысын анықтау және бірінші жуықтау метрикасын, шығарудан болады. Негізі ол есептер бөлек шығарылу керек болған, басында Эйнштейн теңдеуі нөлінші жуықтауда шешіліп және ол шешімді ньютондық интервалымен салыстырып
тұрақтысын анықтау және бірінші жуықтау метрикасын, шығарудан болады. Негізі ол есептер бөлек шығарылу керек болған, басында Эйнштейн теңдеуі нөлінші жуықтауда шешіліп және ол шешімді ньютондық интервалымен салыстырып
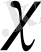 тұрақтысын табады, содан бірінші жуықтауды есептейді.
тұрақтысын табады, содан бірінші жуықтауды есептейді.
2. Орталық-симметриялық гравитациялық өрісте қозғалатын сыналатын дене есебіне (1. 47) өрнекті қолдансақ, онда перигелий ығысуының өрнегі шығады.
3. аралдық жүйе үшін
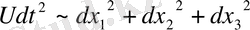
Осы ескертулерді ескеріп
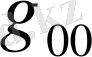 қатысты түзетуді анықтайық.
қатысты түзетуді анықтайық.
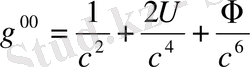 (1. 48)
(1. 48)
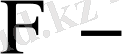 әзірше анықталмаған функция.
әзірше анықталмаған функция.
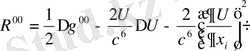 (1. 49)
(1. 49)
Осыған сәйкес Эйнштейн теңдеуі
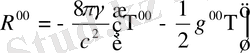 (1. 50)
(1. 50)
Бұл жерде:
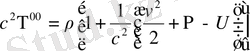 Equation. 3 (1. 51)
Equation. 3 (1. 51)
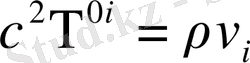 Equation. 3 (1. 52)
Equation. 3 (1. 52)
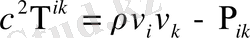 Equation. 3 (1. 53)
Equation. 3 (1. 53)
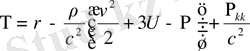 Equation. 3 (1. 54)
Equation. 3 (1. 54)
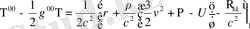 Equation. 3 (1. 55)
Equation. 3 (1. 55)
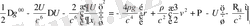 Equation. 3 (1. 56)
Equation. 3 (1. 56)
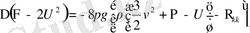 Equation. 3 (1. 57)
Equation. 3 (1. 57)
 Equation. 3 (1. 58)
Equation. 3 (1. 58)
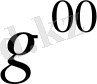 метрикалық тензордың ковариантты компоненті
метрикалық тензордың ковариантты компоненті
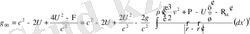 (1. 59)
(1. 59)
Фоктың бірінші жуықтауының нақтылынған метрикасы:
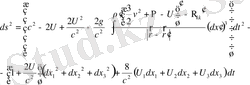 (1. 60)
(1. 60)
Осы метрикадан көрініп тұрғандай, Эйнштейннің гравитация теориясындағы бірінші жуықтау өрістің сызықтық емес, үш өлшемді кеңістіктің қисаюына, айналумен байланысты ішкі құрылым мен векторлық гравитациялық өріске алып келеді. Ал интервалы
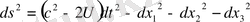 (1. 61)
(1. 61)
болатын Ньютонның гравитациялық теориясы гравитациялық өріс сызықты, айналумен байланысты үш өлшемді кеңістік евклидті екеніне негізделген.
- Орталық өрістегі қозғалыс жайлы есеп.
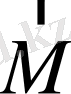 (
импульс моменті
),
(
импульс моменті
),
 (
Лаплас векторы
)
векторлары мен орташалау әдісін қолданып (1. 60) метрикасы көлемінде шығарылады. /2. c. 8., 3. c. 11. /
(
Лаплас векторы
)
векторлары мен орташалау әдісін қолданып (1. 60) метрикасы көлемінде шығарылады. /2. c. 8., 3. c. 11. /
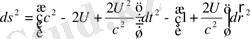 (1. 62)
(1. 62)
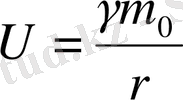 (1. 63)
(1. 63)
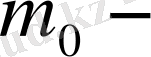 орталық дене массасы
орталық дене массасы
Ньютон жуықтауындағы
 массасы бар бөлшек үшін (1. 60) метрикасы эллипс бойымен кеплер қозғалысын береді.
массасы бар бөлшек үшін (1. 60) метрикасы эллипс бойымен кеплер қозғалысын береді.
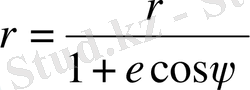 (1. 64)
(1. 64)
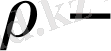 параметр,
параметр,
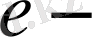 эксцентриситет,
эксцентриситет,
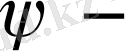 полярлы бұрыш.
полярлы бұрыш.
Орбиталдық полярлы жүйе
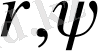 мен төмендегідей қатынаста байланысқан
мен төмендегідей қатынаста байланысқан
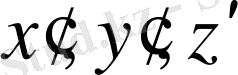 декарттық координат жүйесін енгізейік
декарттық координат жүйесін енгізейік
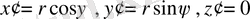 (1. 65)
(1. 65)
Релятивтік емес жуықтауда импульс моменті мен Лаплас векторы сақталады. /4. c. 427/
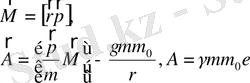 Equation. 3 (1. 66)
Equation. 3 (1. 66)
Релятивтік жуықтауға көшкенде
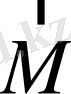 және
және
 векторларын қозғалысты сипатайтын айнымалылар ретінде қолданады. Сонда
векторларын қозғалысты сипатайтын айнымалылар ретінде қолданады. Сонда
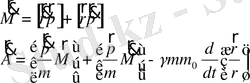 (1. 67)
(1. 67)
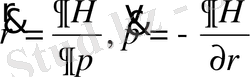 (1. 68)
(1. 68)
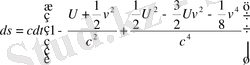 (1. 69)
(1. 69)
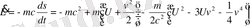 (1. 70)
(1. 70)
Жалпы импульс
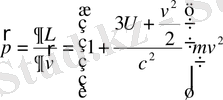 (1. 71)
(1. 71)
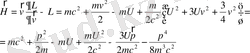 Equation. 3 (1. 72)
Equation. 3 (1. 72)
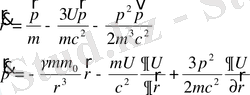 Equation. 3 (1. 73)
Equation. 3 (1. 73)
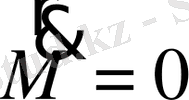 Equation. 3 (1. 74)
Equation. 3 (1. 74)
Бұдан
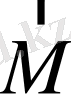 векторы сақталады және қозғалысы жазық болытыны көрінеді.
векторы сақталады және қозғалысы жазық болытыны көрінеді.
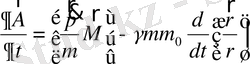 (1. 75)
(1. 75)
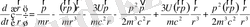 (1. 76)
(1. 76)
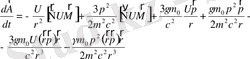 (1. 77)
(1. 77)
Энергияның сақталу заңына сәйкес
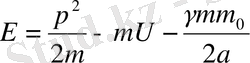 (1. 78)
(1. 78)
 эллипстің үлкен жартылай осі
эллипстің үлкен жартылай осі
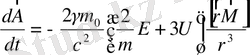 (1. 79)
(1. 79)
Немесе
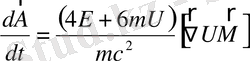 (1. 80)
(1. 80)
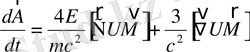 (1. 81)
(1. 81)
Немесе
.
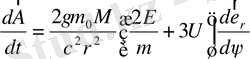 (1. 82)
(1. 82)
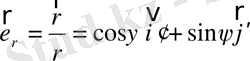 (1. 83)
(1. 83)
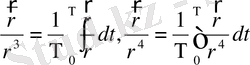 (1. 84)
(1. 84)
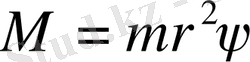 (1. 85)
(1. 85)
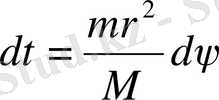 (1. 86)
(1. 86)
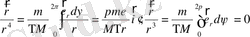 (1. 87)
(1. 87)
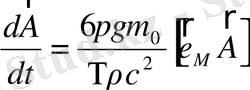
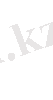 (1. 88)
(1. 88)
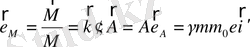 (1. 89)
(1. 89)
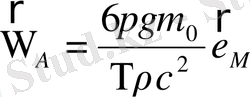 (1. 90)
(1. 90)
 векторы жазықтықта төмендегідей бұрыштық жылдамдықпен айналады
векторы жазықтықта төмендегідей бұрыштық жылдамдықпен айналады
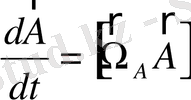 (1. 91)
(1. 91)
 векторының орны жазық орбитада полярлы координаттар
векторының орны жазық орбитада полярлы координаттар
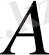 және
және
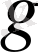 бойынша бейнеленсе, ондаn
бойынша бейнеленсе, ондаn
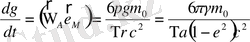 (1. 92)
(1. 92)
 период ішінде полярлық бұрыштың
период ішінде полярлық бұрыштың
 өзгерісі
өзгерісі
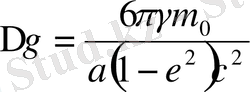 (1. 93)
(1. 93)
2-бөлім. Ішкі құрылымы мен өздік айналысын ескергендегі екі айналмалы дене есебі
2. 1 Лагранж функциясы және қозғалыс теңдеуі
Өздік айналысы бар орталық дене өрісінде орналасқан сыналатын дененің Лагранж функциясы
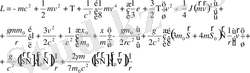 (2. 1)
(2. 1)
J-сыналатын дененің айну осіне катысты инерция моменті.
Қозғалыс теңдеуі
Біз қарастырып отырған есептің қозғалыс теңдеуін, сызықты емес асимптоталық әдістерді қолдану үшін ыңғайлы,
 және
және
 векторларына кетіріп жазайық. /5/
векторларына кетіріп жазайық. /5/
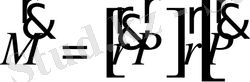 (2. 2)
(2. 2)
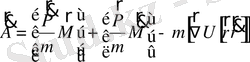 (2. 3)
(2. 3)
Импульс
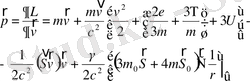 (2. 4)
(2. 4)
Гамильтониан
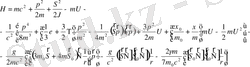 (2. 5)
(2. 5)
Туындылар
 (2. 6)
(2. 6)
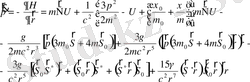 (2. 7)
(2. 7)
мұнда
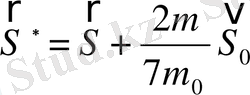 -белгілеу енгіздік.
-белгілеу енгіздік.
(2. 7) мен (2. 6) өрнектерін (2. 3) пен (2. 2) қойсақ, бізге керек қозғалыс теңдеуін аламыз:
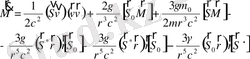 (2. 8)
(2. 8)
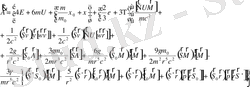 (2. 9)
(2. 9)
Қозғалыс теңдеуін орташалау
(2. 8) мен (2. 9) теңдеулерін интегралдау киын, сондықтан кіші параметрі бар дифферециалдық теңдеулерді жуықтап шешу әдісін қолданамыз, әсіресе сызықты емес механиканың асимптоталық әдісі эффетивті.
Бірінші жуықтаудағы дифференциалдық теңдеулердің асимтоталық әдісі (2. 8) және (2. 9) теңдеулердің оң жағын баяу айнымалыларды тез айнымалыларға орташалау арқылы алынады, сонымен қатар орташалаған кезде кеплердің (айнымаған) айнымалылардыдың мәні қойылады.
Бірінші жуықтаудағы теңдеуді құраймыз. Оған кеплер қозғалысының формулалары қажет. /4/
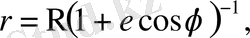
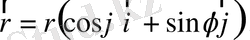
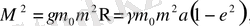
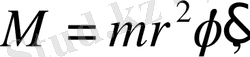
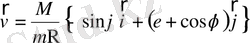
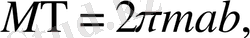 (2. 10)
(2. 10)
(2. 9) мен (2. 10) өрнектері үшін мына теңдік орынды:
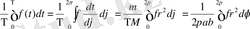 (2. 11)
(2. 11)
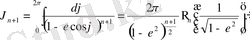 (2. 12)
(2. 12)
Мысал:
1)
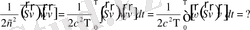 (2. 13)
(2. 13)
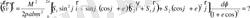 (2. 14)
(2. 14)
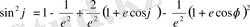 (2. 15)
(2. 15)
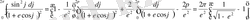 (2. 16)
(2. 16)
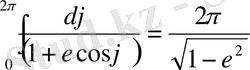 (2. 17)
(2. 17)
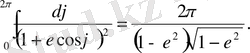 (2. 18)
(2. 18)
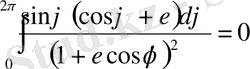 (2. 19)
(2. 19)
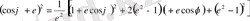 (2. 20)
(2. 20)
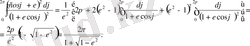 (2. 21)
(2. 21)
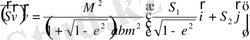 (2. 22)
(2. 22)
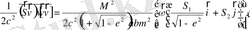 (2. 23)
(2. 23)
2)
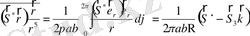 (2. 24)
(2. 24)
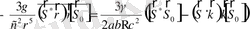 (2. 25)
(2. 25)
3)
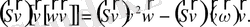 (2. 26)
(2. 26)
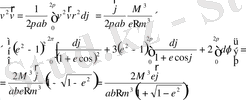 (2. 27)
(2. 27)
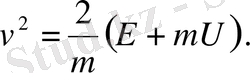 -ауыстыруын енгіземіз
-ауыстыруын енгіземіз
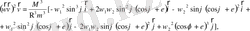 (2. 28)
(2. 28)
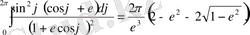 (2. 29)
(2. 29)
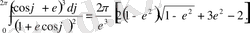 (2. 30)
(2. 30)
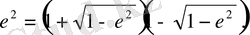
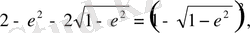
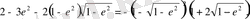 (2. 31)
(2. 31)
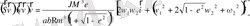 (2. 32)
(2. 32)
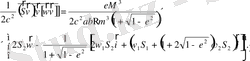 (2. 33)
(2. 33)
Сонда (2. 8), (2. 9) қозғалыс теңделерінің орташаланған түрі:
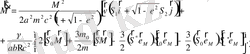 (2. 34)
(2. 34)
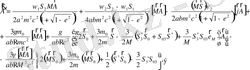 (2. 35)
(2. 35)
Қозғалыс теңдеуін бұрыштық жылдамдықты қолданып түрлендірсек, мына түрге келеді:
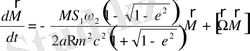 (2. 36)
(2. 36)
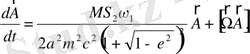 (2. 37)
(2. 37)
2. 2 бірінші жуықтау теңдеуін зерттеу
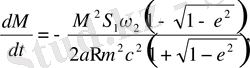 (2. 38)
(2. 38)
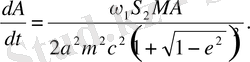 (2. 39)
(2. 39)
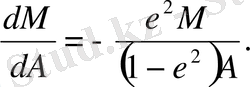 (2. 40)
(2. 40)
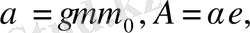 (2. 41)
(2. 41)
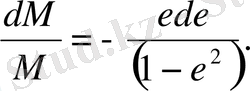 (2. 42)
(2. 42)
Осыдан қозғалыс интегралы шығады:
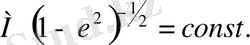 (2. 43)
(2. 43)
Осы өрнектің оң жақ тұрақтысы қарастырылып отырған есептің адиабаталық инварианты болады. Оны
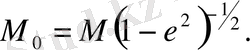 (2. 44)
(2. 44)
деп белгілейік.
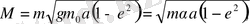 (2. 45)
(2. 45)
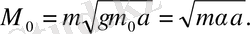 (2. 46)
(2. 46)
«релятивтік емес» энергиямен адиабаталық инвариантының байланысы
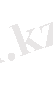
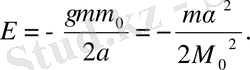 (2. 47)
(2. 47)
Табылған инварианттын көмегімен бірінші жуықтау теңдеуідегі тәуелсіз айнымалылар санын бірге кемітуге болады. Сондай айнымалы
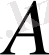 таңдап алсақ, теңдеу тек
таңдап алсақ, теңдеу тек
 ,
,
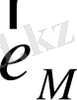 және адиабаталық инвариант
және адиабаталық инвариант
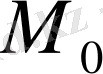 құралатын болады. Яғни
құралатын болады. Яғни
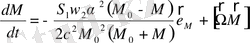 (2. 48)
(2. 48)
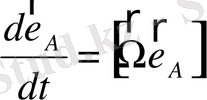 (2. 49)
(2. 49)
Осы екі өрнекті келесі үш теңдеуге жіктейміз
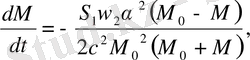 (2. 50)
(2. 50)
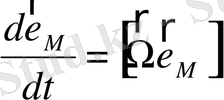 (2. 51)
(2. 51)
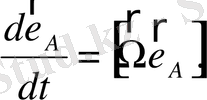 (2. 52)
(2. 52)
1)
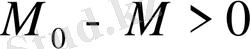 болғандықтан, туынды
болғандықтан, туынды
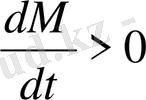 , егер
, егер
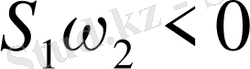 және керісінше болса.
және керісінше болса.
(2. 44) сәйкес
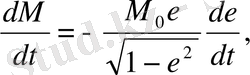 (2. 53)
(2. 53)
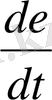 -таңбасы
-таңбасы
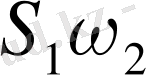 таңбасымен сәйкес келеді.
таңбасымен сәйкес келеді.
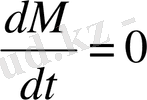 егер
егер
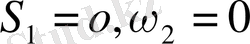 , немесе
, немесе
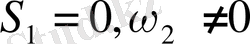 , немесе
, немесе
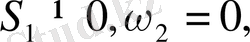 немесе
немесе
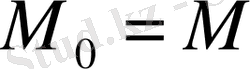 , яғни
, яғни
 .
.
2)
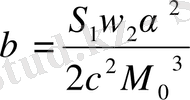 белгілеуін енгізіп (2. 50) өрнек
белгілеуін енгізіп (2. 50) өрнек
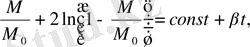 (2. 54)
(2. 54)
немесе
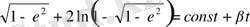 (2. 55)
(2. 55)
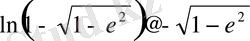 (2. 56)
(2. 56)
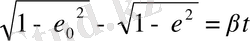 (2. 57)
(2. 57)
 -бастапқы уақыттағы эксцентриситетің мәні.
-бастапқы уақыттағы эксцентриситетің мәні.
3) (2. 41) мен (2. 43) өрнектен
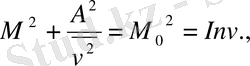 (2. 58)
(2. 58)
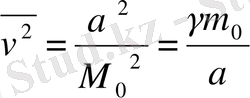 (2. 59)
(2. 59)
«Күй векорын» енгізсек
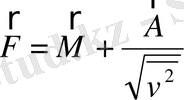 (2. 60)
(2. 60)
Фазалық кеңістікте векторлады
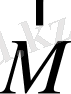 ,
,
 және
және
 векторының соңын эллипс бейнелейді.
векторының соңын эллипс бейнелейді.
4) (2. 51) мен(2. 52) өрнектен сыналатын дене мен онымен байланысқан орбиталды санақ жүйесі бекітілген нүкте бойымен бұрыштық жылдамдықпен айналады
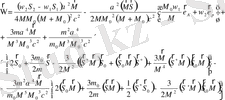 (2. 61)
(2. 61)
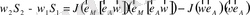 , (2. 62)
, (2. 62)
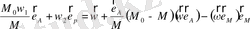 (2. 63)
(2. 63)
 (2. 64)
(2. 64)
5)
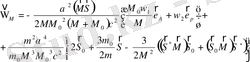 (2. 65)
(2. 65)
 (2. 66)
(2. 66)
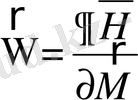 (2. 67)
(2. 67)
2. 3 Екі айналмалы дене есебінің өздік айналысы
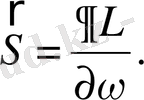 (2. 68)
(2. 68)
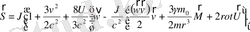 (2. 69)
(2. 69)
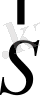 - жалпыланған айналмалы импульс
- жалпыланған айналмалы импульс
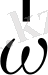 ,
,
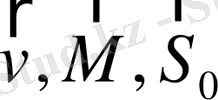 және
және
 пропорционал мүшеслері бар.
пропорционал мүшеслері бар.
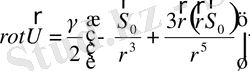 (2. 70)
(2. 70)
егер
 , онда
, онда
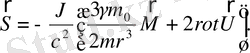 (2. 71)
(2. 71)
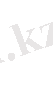
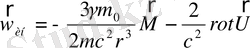 (2. 72)
(2. 72)
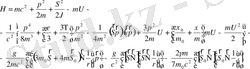 (2. 73)
(2. 73)
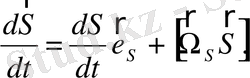 (2. 74)
(2. 74)
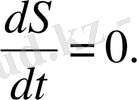 (2. 75)
(2. 75)
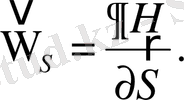 (2. 76)
(2. 76)
Сыналатын дененің айналмалы қозғалыс теңдеуі
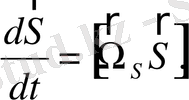 (2. 77)
(2. 77)
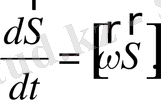 (2. 78)
(2. 78)
(2. 78) айналмалы қозғалыс теңдеуі Брумберг монографиясында /6, с. 311/ алынған
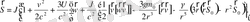 (2. 79)
(2. 79)
Сыналатын дененің айналмаы қозғалыс теңдеуінің орта мәні
 (2. 80)
(2. 80)
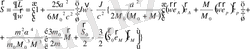 (2. 81)
(2. 81)
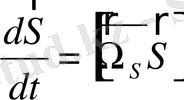 , (2. 82)
, (2. 82)
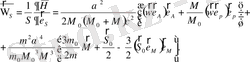 (2. 83)
(2. 83)
2. 4 Екі айналмалы дене есебінің орбиталды және орбитаның векторлық элементтеріне қатысты орнықтылығы
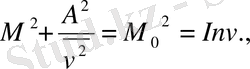 (2. 84)
(2. 84)
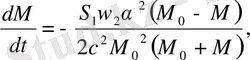 (2. 85)
(2. 85)
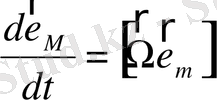 (2. 86)
(2. 86)
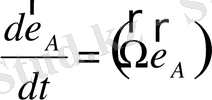 (2. 87)
(2. 87)
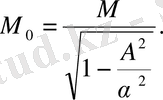 (2. 88)
(2. 88)
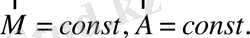 Equation. 3 шарты орындалса, онда
Equation. 3 шарты орындалса, онда
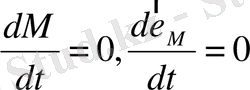 (2. 89)
(2. 89)
Немесе
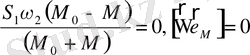 (2. 90)
(2. 90)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz