Дененің айналуы

Жоспар
Кіріспе

1 Сфералық қозғалыс. Эйлер бұрыштары. Сфералық қозғалыстың теңдеулері
2 Қозғалмайтын бір нүктесі бар қатты дененің кез келген шекті уақыт аралығындағы орынауыстыруы туралы теорема (Даламбер.Эйлер теоремасы).
3 Лездік айналу өсі
4 Дененің сфералық қозғалысы кезіндегі бұрыштық жылдамдығы мен бұрыштық үдеуі
5 Бір нүктесінде бекітілген қатты дене нүктесінің сызықтық жылдамдығы
6 Бір нүктесінде бекітілген қатты дене нүктесінің үдеуі.
7 Сфералық қозғалыстың тақырыбына арналған есептер

Қозғалмайтын нүкте төңірегіндегі қатты дененің қозғалысын сфералық қозғалыс деп атайды. Қозғалмайтын нүкте төңірегіндегі қатты дененің қозғалысы сфералық қозғалыс деп аталу себебі бұл нүктеден өзге нүктелердің бәрі радиустары әр-түрлі болған сфералардың бетінде қозғалатын болып, олардың ортақ центрі қозғалмайтын нүктеде жатады. Мысал ретінде гироскоптың, волчоктың қозғалыстарын алуға болады.
Өзге жоғарыда қаралған қозғалыстар сияқты бұл қозғалыс үшін де дененің кез-келген уақыттағы орнын анықтайтын параметрлерді табуға әрекет жасайық. Бұл жерде ең көп тарағаны Эйлердің ұсынған параметрлері. Соған тоқталайық.
Дененің қозғалмайтын О нүктесінен өтетін қозғалмайтын хОуz координаттар жүйесін алайық (12.1-сурет). Басқа х1Оу1z1 координаттар жүйесін дененің тікелей өзімен байланыстырайық. Олай болса дененің хОуz координаттар жүйесіне қатысты кез-келген уақыттағы алатын орнын анықтау үшін қозғалатын санақ жүйесінің қозғалмайтын санақ жүйесіне қатысты алатын орнын беру жеткілікті. Бұл үшін Эйлер бір-біріне тәуелді болмаған үш бұрышты енгізуді ұсынды. Олар прецессия y, нутация q және өзіндік айналу j бұрыштары.

Пән: Физика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 25 бет
Таңдаулыға:

ХII ТАРАУ
. ҚОЗҒАЛМАЙТЫН НҮКТЕ ТӨҢІРЕГІНДЕГІ ҚАТТЫ

ДЕНЕНІҢ АЙНАЛУЫ

12.1 Сфералық қозғалыс. Эйлер бұрыштары. Сфералық қозғалыстың теңдеулері.
Қозғалмайтын нүкте төңірегіндегі қатты дененің қозғалысын сфералық қозғалыс деп атайды. Қозғалмайтын нүкте төңірегіндегі қатты дененің қозғалысы сфералық қозғалыс деп аталу себебі бұл нүктеден өзге нүктелердің бәрі радиустары әр-түрлі болған сфералардың бетінде қозғалатын болып, олардың ортақ центрі қозғалмайтын нүктеде жатады. Мысал ретінде гироскоптың, волчоктың қозғалыстарын алуға болады.
Өзге жоғарыда қаралған қозғалыстар сияқты бұл қозғалыс үшін де дененің кез-келген уақыттағы орнын анықтайтын параметрлерді табуға әрекет жасайық. Бұл жерде ең көп тарағаны Эйлердің ұсынған параметрлері. Соған тоқталайық.
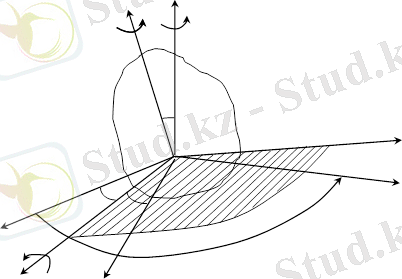
Дененің қозғалмайтын О нүктесінен өтетін қозғалмайтын хОуz координаттар жүйесін алайық (12.1-сурет). Басқа х1Оу1z1 координаттар жүйесін дененің тікелей өзімен байланыстырайық. Олай болса дененің хОуz координаттар жүйесіне қатысты кез-келген уақыттағы алатын орнын анықтау үшін қозғалатын санақ жүйесінің қозғалмайтын санақ жүйесіне қатысты алатын орнын беру жеткілікті. Бұл үшін Эйлер бір-біріне тәуелді болмаған үш бұрышты енгізуді ұсынды. Олар прецессия y, нутация q және өзіндік айналу j бұрыштары.
z1 z
12.1-сурет

х1Оу1координат жазықтығы қозғалмайтын хОу жазықтығымен түйіндер сызығы деп аталатын ОК түзуі бойлап қиылысқан болсын дейік.
Қозғалмайтын Ох өсімен түйіндер сызығының арасындағы бұрыш прецессия бұрышы деп аталып y әрпімен белгіленеді. y бұрышы өзгеріп отыруы үшін дене Оz өсінің төңірегінде айналуы керек, бұл өсь прецессия өсі деп аталады. y бұрышы оң деп есептелінеді, егер Оz өсінің оң ұшынан қарап отырған бақылаушы Ох тан ОКға бұрылу сағат тіліне қарама-қарсы бағытта көрінетіндей болса.
Түйіндер сызығы мен қозғалатын Ох1 өсінің арасындағы бұрыш өзіндік айналу бұрышы деп аталып, j әрпімен белгіленеді. j бұрышы өзгерген кезде дене өзіндік айналу өсі деп аталатын Оz1 дің төңірегінде айналады. j бұрышы оң деп есептелінеді, егер бақылаушы Оz1 өсінің оң ұшынан қарағанда оған ОК дан Ох1 ге бұрылу сағат тіліне қарама-қарсы бағытта орындалатындай болса.
хОу пен х1Оу1 жазықтықтарының, немесе Оz пен Оz1 өстерінің арасындағы бұрыш нутация бұрышы деп аталып q әрпімен белгіленеді. q өзгергенде дене нутации өсі деп аталатын ОК ның төңірегінде бұрылады. q бұрышы оң деп есептелінеді, егер ОК ның оң ұшынан қарап отырған бақылаушы, поворот от оси Оz өсінен Оz1 өсіне бұрылу сағат тіліне қарама-қарсы бағытта орындалатындай болса.
Эйлер бұрыштары қозғалатын санақ жүйесінің қозғалмайтын санақ жүйесіне қатысты алатын орнын бірден-бір анықтайтын координаталар, демек бұл координаталар қозғалмайтын нүктесі бар дененің қозғалысын да зерттеуге мүмкіншілік береді.
Сонымен қозғалмайтын нүкте төңірегінде қатты дененің айналуы кезіндегі оның теңдеулері
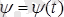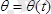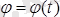; ; , (12.1)
мұндағы 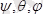- Эйлер бұрыштары, ол денемен қатты бекітілген 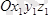жүйенің қозғалмайтын 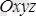жүйеге қатысты кез-келген уақытта алған орнын анықтайды (12.1- сурет ).
Эйлер бұрыштарынан пайдаланып, дененің әр-бір уақыт аралығындағы бұрыштық жылдамдығы мен бұрыштық үдеуін және дененің әр-бір нүктесінің жылдамдығы мен үдеуін анықтауға болады.

12.2 Қозғалмайтын бір нүктесі бар қатты дененің кез келген шекті уақыт аралығындағы орынауыстыруы туралы теорема (Даламбер-Эйлер теоремасы).

Ø Теорема. Қозғалмайтын бір нүктесі бар қатты дененің кез келген орынауыстыруын оны қозғалмайтын нүкте арқылы өтетін өсь төңірегінде белгілі бір бұрышқа айналдыру арқылы орындауға болады. Дәлелдеу. Қатты дененің кеңістіктегі кез келген орынауыстыруы оның бір түзудің бойында жатпайтын үш нүктесінің координаталарымен анықталады. Егер оның бір нүктесі қозғалмайтын болса, онда оның орны осы қозғалмайтын нүктемен бір түзудің бойында жатпайтын екі нүктесінің координаталарымен табылады. Теореманы дәлелдеу үшін қозғалмайтын О нүктесі орталық болатын сфералық бетті аламыз (12.2-сурет).

12.2-сурет
Осы бетке қатысты екі А және В нүктелерін таңдаймыз. Онда бұл дененің орны осы сфераның ең үлкен шеңберінің АВ доғасы арқылы анықталады. Дене өз орнын ауыстырған кездегі АВ доғасының жаңа орны А1В1 болсын. Енді А нүктесі мен А1 ді, В нүктесі мен В1 ді сфераның ең үлкен шеңберінің доғаларымен қосып, бұл доғаларды D және Е нүктелермен тең екіге бөлеміз. Осы нүктелерден АА - 1 және ВВ1 доғаларға Р* нүктесінде қиылысқанға дейін перпендикулярлар жүргіземіз. Р* нүктесі А және А1 ден В және В1 ден бірдей қашықтықта.
Олай болатын болса АВР* және А1Р*В1 сфералық үшбұрыштар өзара тең. Бұл үшбұрыштардың теңдігінен ÐАР*В =ÐА1Р*В1 келіп шығады. Осы теңдіктің екі жағына да ÐА1Р*В1 қоссақ, онда
ÐАР*В + ÐАР*В1 = ÐА1Р*В1 + ÐАР*В1,

немесе
ÐАР*А1 = ÐВР*В1 = Da.
болады.
Енді денені ОР* өсінің төңірегінде Da бұрышқа бұрсақ, онда АВ және А1В1 доғалары бір-бірінің үстеріне түседі. Демек дененің АВ доғасымен анықталатын орны ол қозғалғанда А1В1 доғасымен анықталатын орнына денені ОР* өсінің төңірегінде бір айналдырғаннан түсуге болады.
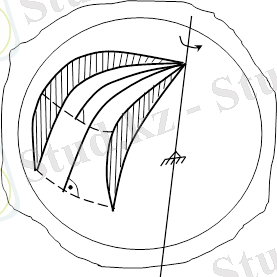
12.3 Лездік айналу өсі
Даламбер-Эйлер теоремасында ОР* өсі шекті айналу өсі, ал Da- шекті айналу бұрышы деп аталған еді. Егер уақыт аралығы Dt(R)0 болса, онда шекті айналу өсі кеңістікте алатын орнын өзгерте отырып өзінің шегіне ұмтылуға әрекет етеді. Dt(R)0 кездегі шекті айналу өсінің шегі t уақыт кезеңі үшін лездік айналу өсі деп аталады. Лездік айналу өсі дененің берілген уақыт кезеңіндегі жылдамдықтары нөлге тең болған нұктелерінің геометриялық орны. Сонымен дененің сфералық қозғалысы кезінде
1) әр-бір кезең үшін қозғалмайтын нүктеден өтуші лездік айналу өсінің болары сөзсіз;
2) лездік айналу өсінің кеңістікте алатын орны уақытқа байланысты үздіксіз өзгеріп отырады;
3) сфералық қозғалысты құрайтын денені қозғалмайтын нүктеден өтуші кетпе-кет орын ауыстырып отыратын өсь төңірегінде үздіксіз айналу қатарынан тұрады деп қарастыруға болады.
Сонымен қаралып отырған жағдайдайдың қозғалмайтын өсьті айналудан өзгешілігі дененің бұрыштық жылдамдығы уақыт өтуімен байланысты тек шамасы жөнінен ғана емес, бағыты жөнінен де өзгеріп отырады. Олай болса жалпы жағдайда лездік айналу өсі әр уақыт кезеңінде әртүрлі. Демек, лездік айналу өсьтерінің геометриялық орны төбесі О нүктесінде болатын конустық бет құрайды.
Лездік айналу өсьтерінің қозғалмайтын хОуz координаттар жүйесіне қатысты алатын геометриялық орны қозғалмайтын аксоид, ал қозғалатын х1Оу1z1 координаттар жүйесіне қатысты алатын геометриялық орны қозғалмалы аксоид деп аталады
Сонымен қатар қозғалмалы аксоид қозғалмайтын аксоидтың бетімен сырғанамай домалайды.

12.4 Дененің сфералық қозғалысы кезіндегі бұрыштық жылдамдығы мен бұрыштық үдеуі

Дененің сфералық қозғалысы кезінде t уақытқа сәйкес келетін оның орны I, ал t + Dt уақытқа сәйкес келетін орны II болсын (12.3-сурет). Онда Даламбер-Эйлер теоремасына сәйкес, денені I-орнынан II-орынға өткізу үшін төңірегінде Da бұрышқа бұратындай ОР* өсі табылады. Бұл кезде бұрыштық жылдамдығық
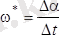(12.2)
өрнектен табылып, ОР* өсі бойлап бағытталады. Dt(R)0 болса, онда w* өзінің бір шегіне ұмтылады. Dt(R)0 да w* ның бұл шегі белгілі уақыттағы дененің лездік бұрыштық жылдамдығы деп аталады және оның шамасы төмендегідей өрнекпен анықталады:

Р*
Р

12.3-сурет

. (12.3)

Ескерту. Бұл шек әрине 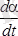ға тең емес, себебі Da a функцияның арттырмасы емес.
векторы лездік айналу өсі бойлап солай бағытталуы керек оның ұшынан қарағанда дененің айналуы сағат тіліне қарама-қарсы бағытта орындалуы шарт. Лездік айналу өсінің алатын орны уақытқа тәуелді болғандықтан оның тек модулі ғана емес, бағыты да өзгереді. Егер жоғарыда бұрыштық жылдамдықты тапқандай тәсілді бұл жерде де қолдансақ, онда дененің бұрыштық үдеуі мына формуламен анықталады:
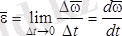. (12.4)
Бұрыштық үдеудің векторы бұрыштық жылдамдықтан уақыт бойынша алынған бірінші туындыға тең. Енді бұрыштық үдеудің бағытын анықтайық. Бұл үшін қозғалмайтын О нүктесінен кетпе-кет уақытқа сәйкес келетін бұрыштық жылдамдықтарды өткізейік. Одан кейін бұл векторлардың ұштарын қосып бұрыштық жылдамдықтың годографын табамыз (12.4-сурет). векторының ұшы болған А нүктесінің жылдамдығын деп белгілейік. Бұл нүктенің радиус-векторы . Сондықтан
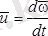(12.5)
болып, бұрыштық жылдамдықтың годографының жанамасы бойлап бағытталған. Бірақ 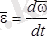. Олай болса , яғни бұрыштық үдеу бұрыштық жылдамдық векторының ұшы болған А нүктесінің сызықтық
жылдамдығына тең.
векторы қозғалмайтын О нүктесінен бастап қойылады. Бұрыштық үдеуі бағытталған ОЕ өсі бұрыштық үдеу өсі деп аталады. Сонымен сфералық қозғалыстың қозғалмайтын өсь төңірегіндегі дененің қозғалысынан айырмашылығы мұның бұрыштық үдеуінің бағыты бұрыштық жылдамдықтың бағытымен дәлме-дәл түспейді.
Егер 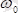арқылы лездік өсінің бірлік векторы белгіленгендей болса, онда 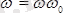. Демек
;
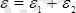Бұл жерде
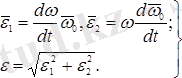(12.6)

(12.6) дағы 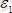векторы лездік өсі бойлап бағытталып, векторының тек жылдамдығының шамасының өзгеруін сыйпаттайды. 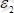векторы болса векторының жылдамдығының бағыт бойынша өзгеруін көрсетеді. Егер векторының айналған кездегі бұрыштық жылдамдығын 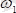деп белгілесек,онда

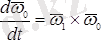
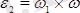. (12.7)
және векторларын қозғалмайтын О нүктесіне қойылған деп есептейміз.
Қозғалмайтын өстерге болған лездік бұрыштық жылдамдық векторының проекцияларын анықтайтын формулалар төмендегідей көрініске ие болады:
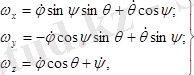(12.8)
Ал денемен тікелей байланыста болған өстерге бұрыштық жылдамдықтың проекциялары мына өрнектермен табылады
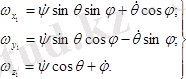(12.9)
Бұрыштық жылдамдықтың шамасы
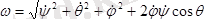(12.10)
тең.

Р

12.4-сурет

12.5 Бір нүктесінде бекітілген қатты дене нүктесінің сызықтық жылдамдығы. Лездік айналу өсінің теңдеуі.

Дененің сфералық қозғалысын әр-бір кезең үшін қозғалмайтын нүктеден өтетін лездік өсінің төңірегінде оның айналуынан тұрады деп қарастырсақ болады. Сол себептен де дененің кез келген М нүктесінің жылдамдығын Эйлер формуласы арқылы анықтаймыз, яғни
(12.11)
Бұл жердегі - қозғалмайтын О нүктесінен өтетін М нүктенің радиус-векторы. Олай болса бұл нүктенің жылдамдығы мына формуламен табылады:
v 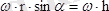. (12.12)

Мұндағы h - М нүктесінің лездік айналу өсіне дейінгі өзгеріп отыратын арақашықтығы
Р

12.5-сурет

(12.13)

(12.13) тегі 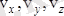- қозғалмайтын координаттар өстеріне болған жылдамдықтың проекциялары; 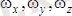- бұрыштық жылдамдықтың қозғалмайтын координаттар өстеріне болған проекциялары; х,у,z-қаралып отырған нүктенің қозғалмайтын өстерге қатысты координаттары.
Жоғарыда келтірілген формулаларды қозғалатын координаттар өстеріне де қатысты жазуға болады. Егер дененің сфералық қозғалысын зерттеп отырған шақта лездік айналу өсінде жататын оның бірер-бір нүктесін алсақ, онда бұл нүктенің радиус-векторы мен бұрыштық жылдамдық бір түзудің бойымен бағытталады. векторы зерттеліп отырған кездегі жылдамдықтары нөлге тең болған нүктелерден өтетін лездік өсі бойлап бағытталған. Егер бір конусты құрайтын қатты дене екінші бір конусты құрайтын дененің бетімен сырғанамай қозғалатын болса, онда лездік өсі осы конустардың ортақ жанасқан нүктелерін қосушы түзу болып есептелінеді. Бұл өстің қозғалмайтын өстерге қатысты теңдеуі ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.