MATHCAD-қа электрондық оқулық

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 84 бет
Таңдаулыға:

МАЗМҰНЫ

Кіріспе

I. MATHCAD-қа ҚЫСҚАША ТҮСІНІКТЕМЕ

1. 1 Mathcad нұсқасы

1. 2 Mathcad программасының мүмкіндіктері

1. 3 Mathcad жүйесінің негізі және интерфейсі

1. 4 Mathcad - тың басты объектілері

1. 5 Mathcad алфавиті (әліпбиі)

II. MATHCAD ТІЛІНІҢ ҚОЛДАНЫЛУЫ

2. 1 Кинематика.

2. 2 Материалдық нүктенің және қатты дененің динамикасы.

2. 3 Сақталу заңдары.

2. 4 Молекула-кинетикалық теорияның негіздері. .

2. 5 Термодинамика негіздері.

2. 6 Электростатика.

2. 7 Тұрақты электр тогы.

2. 8 Магнит өрісі. Заттағы магнит өрісі.

2. 9 Электромагниттік индукция. Максвелл теңдеулері.

2. 10 Гармоникалық тербелістер. Электромагниттік тербелістер. Толқындық процестер.

ІІІ. Электронды құралды жасаудың программалық жабдықталуы

3. 1 Delphi ортасының теориялық негіздері. Delphi - ді баптау.

3. 2 Форманың қасиетін өзгерту. Формаға жаңа компоненттер орналастыру.

3. 3 Оқиғаға жауапты қалыптастыру.

3. 4 Delphi ортасының компоненттер палитрасы.

Формалар терезесі.

ҚОРЫТЫНДЫ

ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ

ҚОСЫМШАЛАР

I. Mathcad - қа қысқаша түсініктеме

1. 1 Mathcad нұсқасы

Mathcad 2000 нұсқасы бар мүмкіндіктер қатарын толықтырды: жүйе интерфейсі айтарлықтай жақсарды, жекелей алғанда Интернетпен интеграция ресурс орталығына орналастырылды; қаржы-экономикалық функцияларды, үш өлшемді матрицаларды шешуге, Given есептеу блогында дифференциалдық теңдеулерді сандық түрде шешуге арналған функциялар қатары енгізілген; логорифмді, синусоидалы, экспоненциалды және т. б. регрессияларды орындауға арналған функциялар қатары; логикалық операторлар жиыны; root функциясының мүмкіндіктерінің артуы - ол енді түбірді тек берілген жуықтау арқылы (екі параметрлі функция) ғана емес, берілген интервал арқылы (төрт параметрлі функция) да іздей болады; үш өлшемді графикті тез әрі ықшамды тұрғызу; ресурстар орталығында мысалдар жиынтығы айтарлықтай жаңартылған.

1. 2 Mathcad программасының мүмкіндіктері

Қолданбалы есептерді шығаруда дүние жүзілік мамандардың алдында компьютерлік математиканың әмбебаб программалық жүйелерін(Mathcad, MathLab, Mathematica, Maple) қолдану мүмкіндігі туып отыр. Осы аталған компьютерлік математика жүйелерінің ішінде Mathcad Pro жүйесі әйгілі америкалық MathSoft фирмасының кәсіптік нұсқасы болып табылады. Бұл жүйенің төмендегідей ерекшеліктері бар:

қарапайымдылығы;
қолданушыға программистке сияқты жоғарғы талаптың болмауы;
деректерді әртүрлі форматта бейнелеу және түрлендіру мүмкіндіктерінің болуы;
математикалық өрнектердің, символдық түрлендірулер операторларының қуатты арсеналының болуы;
түсіндірме хат, есеп берулер, мақалалар, монографиялар жазуда мәтіндік редактор мен Mathcad құжатының фрагменттерін қатар қолдану мүмкіндігінің болуы;
«шаблондар» жиымы мен кез келген математикалық есептерді (алгебралық және дифференциалдық теңдеулер жүйесін, теңсіздіктерді, циклдық және рекуренттік процедураларды шешу т. с. с. ) шығаруда қолданылатын кіріктірілген функциялардың(алдын ала С++ тілінде программаланған) болуы;
Mathcad- жүйесінде символдық және сандық есептеулер жүргізуге болады. Сандық мәндер символдық есептеулер тізбегінен тұруы мүмкін.
Mathcad-та барлық элементар формулалармен қатар элементар емес функциялар да кіріктірілген.
бөлшектерге амалдар қолдану;
теңдеулер, теңдеулер мен теңсіздіктер жүйесі;
алгебралық теңдеулердің 4-ші дәрежеде есептелуі(квадрат теңдеу,

кубтық теңдеу, тригонометриялық теңдеу, калинион және рационал

теңсіздіктер.

дифференциалдау;
интегралдау;
қосынды мен көбейтіндіні есептеу;
математикалық статистика есептерінің фигуралары үшін графиктер

тұрғызу.

Mathcad-тың жаңа мүмкіндіктері арнайы кеңейту топтамасымен және жүйені толықтыра түсетін қосымша функциялармен, арнайы есептерді шешуге арналған тұрақтылармен қамтылған кітапханалар көмегімен толыға түседі:

Берілгендерді анализдеу топтамасы(ағыл. Data Analysis Extension Pack) - Mathcad -ты берілгендерді анализдеуге қатысты қажетті құралдармен қамтамасыз етеді.
Сигналдарды өңдеуге қатысты топтама(ағыл. Signal Processing Extension Pack) - құрамында анализдеу, нәтижені графикалық түрде ұсыну, сигналдарды аналогтық және сандық түрде өңдеуге арналған 70-тен астам кіріктірілген функциясы бар.
Бейнені өңдеуге арналған топтама(ағыл. Image Processing Extension Pack) - Mathcad -ты бейнені өңдеуге, анализдеуге және визиуализациялауға мүмкіндік беретін қажетті құралдармен қамтамасыз етеді.
Толқынды түрлендіру функцияларымен жұмыс істеуге арналған топтама(ағыл. Wavelets Extension Pack) - Mathcad Professional базалық модулінің кіріктірілген функциялар кітапханасына енгізуге болатын қосымша вейвлет-функциялардың үлкен жиынтығына ие топтама. Топтама сигналды және бейнені анализдеуге, сигналдарды статистика тұрғысынан бағалауға, мәліметтерді қысуға және арнайы сандық әдістерге басқаша қатынас жасауға мүмкіндік береді. Топтама құрамына 60-тан астам кілттік вейвлет функциялары кіреді. Вейвлет әулетінің ортогональды және биоортагональды функцилары да кіріктірілген, жеңілдері қатарында- Хаара вейвлеті, Добеши вейвлеті, симлет, койфлет және B-сплайндар. Сонымен қатар, топтама құрамына негізгі вейвлет принципіне негізделген кеңейтілген диалогты құжаттама, қосымшалар, мысалдар және сілтемелер кестесі.
Құрылыс кітапханасы(ағыл. Civil Engineering Library) - англ. Roark's Formulas for Stress and Strain(Формулы Роарка для расчета напряжений и деформаций) анықтамалығын, құрылыс жобалауына арналған түзетілетін шаблондарды және жылу есептерінің мысалдарын іске қосады.
Электротехникалық кітапхана(ағыл. Electrical Engineering Library) - құрамында электортехникада қолданылатын анықтамалық кестелер, стандартты есептеу процедуралары және формулалар бар. Мәтіндік түсіндірулер және мысалдар кітапханамен жұмысты жеңілдетеді- әрбір көрсеткішке және тарауға тақырыпшалар арқылы сілтеме қойылған және сол сілтеме арқылы оны іздеу жүйесінен таба аламыз.
Машина жасау кітапханасы(ағыл. Mechanical Engineering Library) -құрамына 5 мыңнан астам формулалар кіретін және McGraw-Hill анықтамалығынан алынған процедуралар енетін ағыл. Roark's Formulas for Stress and Strain(Формулы Роарка для расчета напряжений и деформаций) анықтамалығын және ақырғы элементтер әдісін іске қосады. Мәтіндік түсіндірулер, келтірілген мысалдар және іздеу жүйелері жұмысты едәуір жеңілдетеді. Анақтамалықтың құрамына Дэвид Пинтурдың «Ақырғы элементтер әдісіне кіріспе» атты электоронды кітабы енгізілген.

1. 3 Mathcad жүйесінің негізі және интерфейсі

Mathcad -тың аналогтық программалардан негізгі ерекшелігі - ол өрнекті енгізудің мәтіндік емес, графикалық режимі. Командаларды, функцияларды және формулаларды енгізу үшін пернетақтаны және де көптеген арнайы құрал саймандар панеліндегі батырмаларды пайдалануға болады. Қандай жағдайда да енгізілген формулалар қалыпты түрге ие болады. Яғни формуланы енгізу үшін арнайы білім талап етілмейді. Енгізілген формулаға есептеу жүргізу қолданушының қалауымен, бірмезетте, барлық жиынға бірден немесе команда бойынша жүргізіледі. Қарапайым формулалар солдан оңға және жоғарыдан төменге қарай есептелінеді. Басқа прогаммаларда (Maple, MuPAD, Mathematica) есептеу программалық интрепретатор режимінде жүзеге асады. Maple интерфейсі дәстүрлі программалау тілдерінде жұмыс істеу дағдыларына ие қолданушыларға арналған. Mathcad-та жұмыс істеу үшін программалау дағдыларын меңгеру міндеттелмейді. Mathcad жүйесінің түсінікті графикалық интерфейстері бар. Mathcad интерфейсінде меңзер арқылы жұмыс істеу барысында обьектілерге мынандай амалдар қолдану керек:

Көрінген барлық хабарламаны және өзгертілген жұмыс алаңың белгілеу.
Өзінің экспериментін қою.
Тышқанның оң және сол батырмаларын шерту арқылы олардың қасиеттерін зерттеп ерекшелеу.
Басты мәзірдегі командалардың аудармаларына көңіл аудару.

Басты терезе жүйесі және интерфейс элементтері

Mathcad программасын іске қосу үшін:

Бастау → Бағдарламалар → MathSoft Apps → Mathcad 2000 Professional

Mathcad -іске қоқаннан кейін басты терезе ашылады. Басты терезе жүйесі 1. 2. 1 - суретте көрсетілген. Баптау жүргізілгеннен кейін, қолданушыға жұмыс жасауға ыңғайлы терезенің түрін алуға болады. Терезедегі басты көрінетін элементтер 1-ден 11-ге дейін белгіленген.

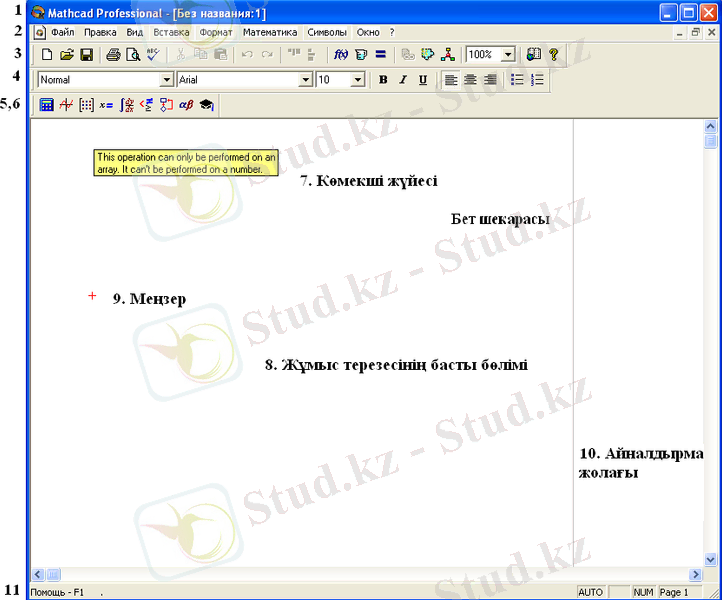
1. 2. 1-сурет. Басты терезе жүйесі

1- ашылған құжаттың тақырыбы.

2- жүйенің басты мәзірі орналасқан, құжаттың барлық функцияларына және программаларына командалық қатынас жасауға осыған байланысты. Оң жақ бұрыш бөлігінде құжатты басқару батырмалары орналасқан.

(3-6) құрал саймандар панелі орналасқан.

Standard - стандартты құралдар панелі(3) .
Formatting- форматтау панелі(4) .
Math- математикалық панелі(5) .
Resources- ресурстар панелі(6) .

Көп қолданылатын тематика командасында тоғыз енгізу батырмасы бар - Math панелінде барлық құралдар жылжымалы және оларды терезенің жақтауларына да орналастыруға болады.

Mathcad-ты ашқанда құралдар оның алдында жұмыс істеген позиция орнында тұрады.

Құралдар батырмаларында көмекші жүйесі (7) де бар.

Басты бөлігі - жұмыс терезесі (8), ол математикалық мәндерді, мәтінді, графикті және кестені енгізгенде облыс астынан беріледі. Экранды үнемі математикалық мәндерді және мәтінді енгізуге арналған облыстың басында кішірек меңзер (9) орналастырылған. Ол қызыл крестик түрде болады. Жаңа құжат басталатын терезенің оң жақ бөлігіндегі вертикальды түзуді байқауға болады. Төменгі және оң жақ бөлігінде жолақ (полоса ) және горизонтальды, вертикальды айналдыралмалар орналасқан.

Пунктирлі түзу беттің төменгі шекарасында терезенің вертикальды айналдырмасы шығады. Төменгі шекара, қасындағы шекараға қарағанда «жұмсақ» болып табылады. Төменгі қалып күй жолы басты ақпаратты көрсетеді. Mathcad-та әртүрлі объектілерді орналастыруға болады.

1. 4 Mathcad - тың басты объектілері

Қара төртбұрышты шаблон маркерлері суреттің сол жақ бөлігінде бірден көзге түседі. Нұсқа операциялары сандармен, айнымалылармен, құрмалас мәндермен, операндтармен толтырылады.

Құжатты енгізуде және түзетуде меңзер екі элементтен вертикальды және горизонтальды көк түсті үзінділерден тұрады. Вертикальды үзінді енгізу және түзету орнын, горизонтальды - енгізілетін элементтің мәнін көрсетеді. Енгізу кезінде бұрыштық меңзер түгелдей біртұтас элемент сияқты басып тұрады. Мұндай меңзерді оң бұрыштық көрсеткіш деп атайды. Оң бұрыштық көрсеткішке «Insert» батырмасын қолданамыз.

Күрделі математикалық мәндерді құрғанда бос орын батырмасының рөлі зор, көрсеткіштен бұрын меңзермен қоршап алып, «Бос орын» батырмасын көп рет қолдану керек. Көп жағдайда жақшалар автоматты түрде қойылады.

Осы тапсырмада «Бос орын» және «^» символын теру кезінде келесі символды теру алдында жақша пайда болады.

Құрал - саймандар тақтасы

Құрал - саймандар тақтасы, әдетте басты мәзір жолағынан кейін орналасады және пиктограммалық батырмалардан тұрады. Топтар шекарасы вертикаль бөлгіштермен белгіленген.

Құрал - саймандар тақтасының негізгі қызметі - жиі қолданылатын командаларды тез шақыру болып табылады. Бейнелер (пиктограммалар) құралдардың функционалдық қызметін ашып бейнелейді.

Пиктограммалық батырмаларды қолданудың мүмкіндіктерін математикалық құжат құру кезінде білуге болады. Алдымен таңдалған шаблон бойынша құжаттың таза бланкісі құрылады. Сақтаудың файлдық жүйесінде оған ат қойылады, содан кейін оған құрамдар (есептің мәтіндік қойылуы, мәліметтер және шарттар, шешу әдістері және т. б) енгізіледі. Қажетіне қарай құрылған құжатты баптау іске асырылады. Есептеу блоктарымен жұмыс ерекше түсініктемені қажет етеді.

Құрал - саймандар тақтасының вертикаль бөлгіштерінің арасында орналасқан батырмалық пиктограммалар блогын тақтаның компоненті ретінде анықтайық.

Mathcad-та үш негізгі құрал - саймандар тақтасы бар:

Standard (стандартты)
Formatting (пішімдеу)
Math (математика)

Mathcad-тағы негізгі құрал Math тақтасы болып табылады. Ол көптеген математикалық командалар тізбегінен тұрады.

Құрал - саймандар тақтасының негізгі қызметі жиі қолданылатын командаларды тез шақыру болып табылады. Бейнелер (пиктограммалар) құралдардың функционалдық қызметін ашып бейнелейді. Әрбір тақтадан алдымен олардың қызметін ашып көрсететін пиктограммаларды алайық. Standard тақтасында өлшеу стақаны өлшеудегі ерекшеліктерге есептеу жүргізетіндігі туралы ескертеді, ал символы есептеу процесінің жылдам іске асу мүмкіндігін көрсетеді, Formatting тақтасында , , символдары мәтінді стандартты түрде пішімдеуге көмектеседі. Үшінші Math тақтасында программалау палитрасы және символды есептеулер палитрасы орналасқан. Құрал-саймандар тақтасында пиктограммалық батырмалар көрсетіледі, қажет емес кезде алып тасталынады немесе қолданушының қажетіне қарай керек обьектіні ерекшелеп жанама мәзірден Customize (Баптау) командасын таңдап өзгертуге болады. Тәжірибелі қолданушы керек емес батырманы тақтадан Alt пернесін басу арқылы оңай алып тастай алады.

Standard (Стандартты) тақтасы

Тақта құралдары Mathcad-та стандартты деп мойындалған командаларды тез орындау үшін тағайындалған. Mathcad-тағы негізгі және орталық құрал ретінде ерекшеленген мәнді басқару элементі тағайындалған.

Тақтада File, Edit, Insert мәзірлерінің көп қолданылатын командалары орналасқан. Олар файлдармен жұмыс істеуді, баптау, функцияны, өлшеу және кейбір обьектілердің бірліктерін қоюды қамтамасыз етеді. Сонымен қатар, тақтада Tools мәзірінен екі позиция: Check Spelling (орфаграфияны тексеру) және Calculate (Есептеу) көрсетілген және де Format мәзірінен Align Across (көлденең туралау) және Align Down (тігінен туралау) алынған.

View мәзіріне масштабтау өрісі (тізім) кірістірілген. Тақтаның соңғы батырмасы - Help мәзірін шақыру батырмасы.

Осылайша, стандарт тақтасында тек Symbolics мәзірінің позициялары көрсетілмеген, өйткені ол стандартты командаларға жатпайды.

Енді әрі қарай Standard тақтасының технологиялық және функционалдық мүмкіндіктерін қарастырайық .

Бірінші батырмалар (1-4) құжатпен жұмыс жасау кезінде файлдық операцияларды орындау тәртібін іске асырады:

- құжаттың таза бланкісі көрсетілген жаңа құжат - құжат құру үшін жаңа жұмыс парағын ашады;
- төменге көрсетілген бағыт жолағы - құрылып жатқан құжаттың мүмкін стильдерінің тізімін ашады;
- ашылған бума бейнесі - тізімнен алдында құрылған және сақталған құжатты таңдау үшін сұхбат терезесін шақырады;
- дискет бейнесі - құрылған және ағымдағы құжаттың өзгерістерін сақтайды немесе жаңа құжатты алғаш сақтау үшін Save as (Қалай сақтау) сұхбат терезесін шақырады.

Құжатты баспаға беру және бақылауды тақтаның келесі компоненттері қамтамасыз етеді (5-7) :

- принтер бейнесі - құрылған құжатты баспаға беру үшін Print (баспаға беру) сұхбат терезесін ашады;
- парақ пен лупа бейнесі - құжатты баспаға беру алдында құжатты алдын ала қарап шығу;
- АВС әріптерін қою бейнесі - орфографияны тексеру.

Математикалық есептеулерді баптауды келесі әрекет блоктары анықтайды:

- қайшы бейнесі - ерекшеленген мәтін немесе формула үзіндісін алмасу буферіне көшіре отырып алып тастайды;
- бірнеше көшірмелер бесінші-ерекшеленген мәтін немесе формула үзіндісін алмасу буферіне көшіруді қамтамасыз етеді.
- портфель бейнесі - ерекшеленген мәтін немесе формула үзіндісін алмасу буферінен қоюды қамтамасыз етеді.
- бағыттаушысы солға бұру - соңғы команданы болдырмауды қамтамасыз етеді.
- бағыттауышты оңға бұру бейнесі - соңғы орындалған

команданы қалыпқа келтіреді.

Құжаттағы формулалар мен обьектілердің орналасуы дәл болмауы мүмкін, сондықтан екі команданы енгізуді қосатын format/align regions мәзірі қарастырылған (13, 14) :

- төменгі шекара бойынша түзулер символының бейнесі - ерекшеленген аймақты көлденең сызық бойынша туралауды қамтамасыз етеді;
- сол жақ шекара бойынша туралау символдарының бейнесі - ерекшеленген аймақты көлденең сызық бойынша туралауды қамтамасыз етеді.

Математикалық процессордің негізгі обьектілері шартты түрде енгізілген функциялары бар формулалар болып табылады:

- функция белгісінің бейнесі - қажет функцияны қою үшін Insert Function (Функцияны қою) сұхбат терезесін шақыруды қамтамасыз етеді.

Шешімдерді өлшеу бірліктерін қолдану арқылы сұрыптауға болады:

- өлшеу функциясының бейнесі - қажет өлшеу бірлігін қою үшін Insert Unit (Бірліктер қою) сұхбат терезесін шақыруды қамтамасыз етеді;
- теңдік белгісінің бейнесі - меңзердің оң жақ және төменгі жағында орналасқан барлық формулаларды есептеуді қамтамасыз етеді;
- тізбек үзіндісінің бейнесі - гипермәтінді сілтемені қоюды қамтамасыз етеді;
- камера бейнесі - стандартты қосымшалардың белгілі бір обьектісін қоюды қамтамасыз етеді. Мысалы, Excel электрондық кестесін қою;
- кесте бейнесі - меңзер тұрған жерге кесте нұсқасын қояды;
- ашылатын тізім - жұмыс парағындағы бейнені үлкейту немесе кішірейту үшін масштаб мәнін орнатуды қамтамасыз етеді;
- сұрақ белгісінің бейнесі - анықтама алу үшін Mathcad Help (Mathcad анықтамасы) сұхбат терезесін шақырады.

Formatting (Пішімдеу) тақтасы

Тақта атрибуттарды (стиль, шрифт және оның өлшемі) өзгертуге арналған үш ашылатын тізімнен тұрады. Сонымен қатар Windows қосымшаларында шрифтті сәндеу(қарайтылған қаріп, жартылай қиғаш, асты сызылған), мәтіндерді туралау, абзацті номерлеу және маркерлеу, индексті мәтіннің жоғарғы және төменгі жағына қосу секілді пиктограммалық батырмалардың типтік жиынтығынан тұрады.

Батырмалардың түрі және әрекеті төмендегідей:

- стиль аты көрсетілген ашылатын тізім - қолданушы жұмыс жасап отырған стильдің атын көрсетеді. Қажет болғанда стильдер тізімін алып, тышқанды шерту арқылы қажет стильді таңдап алуға болады;
- ағымдағы уақытта қолданылып жатқан шрифт аты көрсетілген ашылатын тізім. Қажет болғанда шрифттер тізімін алып, тышқанды шерту арқылы қажет шрифтті таңдап алуға болады;
- ағымдағы уақытта қолданылып жатқан шрифт өлшемі көрсетілген ашылатын тізім;
- B (bold - қарайтылған, I (italic - жартылай қиғаш U (underline - асты сызылған әріптер бейнесі) - ерекшеленген мәтінді, формуланы сәйкесінше өзгертеді;
- мәтінді сәйкесінше солға, орта жақ шетке, оңға қарай туралайды;
- мәтін үзіндісінде маркерді немесе номерді орнатады;
- жол үстінде немесе астындағы белгісі бар айнымалы бейнесі - сәйкесінше символдарды қосуды қамтамасыз етеді.

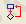
Math (математика) тақтасы

Math тақтасында «палитра» шығару батырмасын жұмыс құжаттарында формула, графиктер, матрицалар, сонымен қатар Mathcad кілттік сөздерін сөндіруге, ажыратуға арналған.

Тақтада көбінесе жұмыс орнынан ауыстыруға қолайлы болады. 1. 2. 23- суретте көрсетілген тақтада жұмыс терезесінің шетінде орналасқан.

Бұл тақтада көрсетілген математикалық құралдар тақтасында көрсетілген түрлі тақталарды ашып, есептерді шешуге мүмкіндік бар.

1. 2. 23-сурет. Math тақтасындағы көмекші жазулар батырмасы.

Батырмалардың түрі мен атқаратын қызметтері мынадай:

- калькулятор белгісі - Cаlculator (калькулятор) сайман тақтасын шақырады, батырма көмегімен стандартты жүйелерді шешеді.
- графика белгісі - Graph (Графика) сайман тақтасын шақырады, батырма көмегімен әр түрлі графикалық есептеулерді салады.
- матрицаға дайындық белгісі - Matriх (матрица) сайман тақтасын шақырады, және батырма көмегімен матрицалық және векторлық жүйелерді шешеді.
- әріптер және белгісіздік теңдіктер белгісі - Evaluation (Выражение) сайман тақтасын шақырады, әріптік және айнымалылық белгілірді енгізумен қатар нәтижесін алады.
- интегралдық және интегралдық белгілер бейнесі - Calculus (математический анализ) сайман тақтасын шақырады, интегралдарды, дифференциялдарды, суммаларды, көбейтіндіні және шексіздіктерді енгізе отырып шешімін алады.
- теңсіздіктер белгілерін бейнелейді - Boolean (Булевые функции) сайман тақтасын шақырады, түрлі теңдеулер жүйелері мен теңсіздіктер санын есептейді.
- блок-схемалар бейнесі - Programming (Программирование) сайман тақтасын шақырады, программалаудың негізгі есептерін шешеді.
- грек алфавитінің әріптерінің бейнесі- Greek (Греческие буквы) грек алфавитінің әріптерін енгізеді.
- академиялық бас киім бейнесі - Symbolic (Символьные вычесление) кілттік сөздердің аналогиялық біліктілігі.

Олардың көмегімен тез арада қиын тапсырманың алгоритмдік шешілімін құрастыруға болады. Сонымен, бізге келесідей командаларды шақыру түрлері белгілі:

мәзірді тышқанның көмегімен басқару;
панельдер тақтасының батырмаларын пайдалану арқылы;
пернетақтадан <Alt>+<әріп>+<әріп>пернелерімен бас мәзірден және аяқтайтын команда мәзірінің үлгісінен;
жылдам шақыру <Ctrl> пернесімен қатар бір мезгілде кілттік пернені басу арқылы;
Контекстілі мәзір арқылы.

1. 5 Mathcad алфавиті (әліпбиі)

Барлық тілдер сияқты (соның ішінде программалау тілдері) Mathcad-қа ену тілінің өз алфавиті бар, яғни объектілерінен тұратын символдар жиыны. Mathcad алфавитіне мыналар кіреді: латынның кіші және үлкен әріптері, гректің кіші және үлкен әріптері, арабтың 0-9 дейінгі сандары, жүйелік айнымалылардың идентификаторлары, арнайы белгілер - операторлар, құрылған функциялар аттары, арнайы белгілер, кириллицаның кіші және үлкен әріптері (орысшаланған құжаттармен жұмыс істеуде) .

Тұрақтылар

Тұрақтылар - мәндері жүйеде анықталған аталған объектілер. Mathcad-та тұрақтының мынадай типтері бар:

Бүтін санды тұрақтылар (0, 1, 23, -45 және т. б. ) ;
Мантиссалы және реттік нақты (вещественные) сандар (12. 3·10-5- 12. 3 мантиссалы және -5 ретті ондық тұрақты) ;
Сегіздік сандар (восьмеричные) - негізі 8 болған, 0-ден 7-ге дейінгі бір разрядты мәндер. (латынның О әріпімен белгіленеді -octal - сегіздік сөзінен шыққан) ;
Он алтылық сандар (шестнадцатиречные) негізі 16 болған, оның әр разряды 0, 1, . . . , 9, A, B, C, D, F мәндерінен тұруы мүмкін (h немесе соңында H әріпімен белгіленеді - hexagional сөзінен шыққан) ;
Комплекстік сандар, мұнда ReZ - Z комплекстік

санының нақты бөлігі, ImZ - оның жорымал бөлігі;

Жүйенің нақты параметрлерін сақтайтын жүйелік тұрақтылар;
Жолдық тұрақтылар - тырнақшаға алынған символдардың кез-келген тізбегі, мысалы, “string”, “2+3” (жолдық тұрақтылардағы арифметикалық өрнектер мәтін ретінде қарастырылады және есептелмейді) ;
Физикалық өлшемдерді өлшеу бірліктері.

* көбейту белгісі экранға санды шығаруда әдеттегі нүктеге айналады, ал дәрежесін табу операциясы (^ арнайы белгіні қолданғанда) дәрежені жол үсті сан түрінде бейнеленеді. Мүмкін сандардың диапазоны 10 ³⁰⁷ -10 ^-307 аралығында жатыр (машиналық шексіздік және машиналық ноль деген осы) .

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.