Қатты денелердің жылу сыйымдылығы және жаңа керамикалық материалдардың SiO2-Al2O3 оксидтерінің температураға тәуелділігі


Мазмұны:
Кіріспе
1. Қатты денелердің жылу сыйымдылығы.
1. 1. Кристалдың жылу сыйымдылығы (классикалық теория)
1. 2 Қатты денелердің молекула- кинетикалық теориясының негізгі
ұғымдары мен түсініктері.
1. 3 Қатты денелердің жылу сыйыдылығының кванттық ұғымдары.
1. 4. Жаңа керамикалық материалдардың құрлымы және қасиеттері.
2. Тәжірибелік тәсілдер және зерттеу нәтижелерін талдау .
2. 1 Зерттеу объектісі, тәжірибелік қондырғы және зерттеу жұмыстарының
әдістері.
2. 2 SiO
 , Al
, Al
 O
O
 тотықтарының жылу сыйымдылығының температураға
тотықтарының жылу сыйымдылығының температураға
тәуелділігі.
3. Жаңа керамикалық материалдардың жылу сыйымдылығын зерттеу
нәтижелері.
Қорытынды.
Қолданылған әдебиеттер.
Кіріспе
Дипломдық жұмыстың бірінші тарауында ең алдымен қатты денелердің жылу сыйымдылығының классикалық теориясын талдап, молекула- кинетикалық теориясының негізгі ұғымдары мен қатты денелердің жылу сыйымдылығының кванттық ұғымдарына тоқталып кетемін.
Жалпы жұмысымның мақсаты- қатты денелердің жылу сыйымдылық процесін зерттеп, температураға тәуелділігін анықтау. Сондықтан зерттеу нысаны ретінде жаңа керамикалық материалдарды алдым. Оған мысал ретінде алюминий мен кремний тотықтарын қолдандым. Соңғы жылдары біздің планетамызда адамзаттың жан -жақты жүргізіп жатқан белсенді қызметтерінің нәтижесінде үлкенді- кішілі экологиялық апаттар орыналуда . . . Бүгінгі таңда жедел дамып отырған ғылыми- техникалық прогрестің нәтижесінде пайда болған осындай үлкен экологиялық проблемалар кездейсоқ пайда болған жоқ.
Экология, технология және өндіріс . . . бұл түсініктердің арасында тығыз байланыс жатыр. Жыл сайын елімізде көмір, химия, энергетика, металлургия және тағы басқа өнеркәсіптермен миллиондаған тонна қалдықтар бөлінуде. Бүгінгі экологиялық проблемалардың бір тамыры міне осындай өнеркәсіп қалдықтарының зиянды әсерлерінен арылу мәселесіне келіп тіреледі. Сонымен экологиялық проблемаларды шешудің белгілі бір бағыты өнеркәсіп қалдықтарын халық шаруашылығының қажетіне жаратудың жан-жақты әдістерін таба отырып, «қалдықсыз», «қалдығы аз » сияқты озықты үнемді технологияларды ойлап табу жұмыстарымен тікелей байланысты. Халық шаруашылығының сан алуан салаларының ішінде әсіресе көмір өнеркәсібінен жыл сайын бөлінетін «қалдықтардың» қоры өте мол. Мысалы: көмірді жерден қазып алу, сонан соң оны арнайы фабрикаларда байыту, дайын болған көмірді жерден қазып алу үшін жағу жолдарының әрқайсысында белгілі бір қалдықтар бөлініп отырады. Осындай қалдықтардың бірі жылу электр станцияларында майда көмір тозаңын жағудан қалатын күл болып табылады. Жағу барысында әр тонна көмірден 30-50 процент шамасында күл бөлініп шығатынын ескерсек, қорының орасан зор екендігі өзінен-өзі түсінікті. Міне, сондықтанда осы жүздеген миллион тонна күлді зиянды қалдықтан кәделі материалдарға айналдыру, яғни тиімді шикізат есебінде пайдалану мәселелері бұл күндері үлкен әлеуметтік проблемаға айналды.
Бұл проблеманың шешілуі әсіресе Екібастұз, Қарағанды сияқты үлкен көмір бассейндері бар. Қазақстан үшін өте маңызды. Қазіргі таңда күл қалдықтарын халық шаруашылығында пайдалану мәселелерін қарастыру жолында біздің еліміздің, сондай-ақ шет елдердің бір қатар ғылыми орталықтарында нәтижелі жұмыстар жүргізілуде. Бұл жұмыстардың барысы күл қалдықтарын сан алуан құрылыс материалдарын жасауда қосымша шикізат есебінде пайдалануға мүмкіндіктер мол екендігін көрсетті.
1. Қатты денелердің жылу сыйымдылығы.
Қатты дененің ішкі энергиясының қоры оны құрайтын бөлшектердің тербеліс энергиясы мен олардың өзара потенциялық энергиясының қоры болып табылады. Кристалдық решетканы жасайтын бөлшектер ( атомдар немесе иондар ), жалпы алғанда, байланыссыз емес, өйткені олардың арасында едәуір өзара әсер күштері болады. Сондықтан бөлшектердің тербелісін байланысты тербеліс деп қарау керек; тұтас решеткада жиіліктері әр түрлі тербелістер болады; олардың энергиялары ескерілу керек. Алайда тербелістің энергиясы үлкен болатын жоғары температураларда бөлшектерді тәуелсіз деп қарастыруға болады. Бөлшектердің әрқайсысы тепе-теңдік қалыптың маңында тербеліп тұрады. Бөлшектің орташа тербеліс энергиясын анықтау үшін, онда кинетикалық энергияның да, потенциялық энергияның да қоры бар екендігін ескеру керек. Орташа есеппен алғанда бұл энергиялардың шамалары бірдей болады. Сонымен, егер бөлшектің орташа кинетикалық энергиясын
 деп белгілесек, онда бөлшектің орташа энергиясының толық мәні
деп белгілесек, онда бөлшектің орташа энергиясының толық мәні
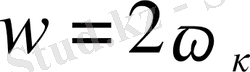 болады.
болады.
Кристалдың кеңістік решеткасында әрбір бөшек өзінің тепе-теңдік қалпының маңында кез келген бағытта тербеле алады; олай болса, оның
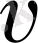 жылдамдығы вектор ретінде қарастырылу керек. Бұдан әрбір бөлшекте
үш
еркіндік
дәрежесі (
і
) бар екендігі шығады. Сондықтан бір бөлшектің орташа кинетикалық энергиясы
жылдамдығы вектор ретінде қарастырылу керек. Бұдан әрбір бөлшекте
үш
еркіндік
дәрежесі (
і
) бар екендігі шығады. Сондықтан бір бөлшектің орташа кинетикалық энергиясы
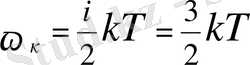 , ал орташа энергияның толық мәні
, ал орташа энергияның толық мәні
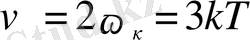
болады.
Қатты дененің бір грамм атомының U толық ішкі энергиясын табу үшін бір бөлшектің орташа энергиясын бір грамм-атомдағы тәуелсіз тербелетін бөлшектердің санына көбейту керек. Химиялық жай қатты кристалл денелердің грамм атомындағы тәуелсіз тербелетін бөлшектердің саны Авогадро санымен N бірдей болады, сондықтан
U
=
 N =
3
NkT
= 3
RT,
(1)
N =
3
NkT
= 3
RT,
(1)
мұндағы R - газ тұрақтысы.
Жылулық ұлғаю коэффициенттері аз болатын қатты денелердің тұрақты көлемдегі және тұрақты қысымдағы жылу сыйымдылықтары іс жүзінде бірдей болады. Сондықтан бұдан бұлай оларды бірдей деп қарастырамыз. Сонда химиялық жай қатты кристалл дененің сан жағынан алғанда ішкі энергияның температура 1°-қа көтерілгендегі артуына тең болатын атомдық жылу сыйымдылығы (1) формула бойынша мынаған тең болады:
C = 3R .
ал газ тұрақтысы
R
 2
2
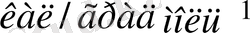 болатындықтан,
болатындықтан,
С
 6
6
 , (1´)
, (1´)
яғни
химиялық жай қатты кристалл денелердің барлығының жеткілікті жоғары температурадағы атомдық жылу сыйымдылығы 6
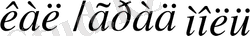 -ға тең болады.
Бұл
Дюлонг
пен
Пти заңы
деп аталады.
-ға тең болады.
Бұл
Дюлонг
пен
Пти заңы
деп аталады.
Кристалды құрастыратын өзара әсерлесетін бөлшектер тербелістерінің сипатын мұқият тексермейінше Дюлонг пен Пти заңы орындалу үшін қарастырылып отырған дененің қандай температурасын жеткілікті жоғары температура деп есептеуге болатындығын алдын- ала айтуға болмайды. Дюлонг пен Пти өздерінің заңын бірқатар денелерге бөлме температурасында жасаған тәжірибелерінің мәліметтерінен қорытып шығарған.
1. 1-ші кестеде бірнеше химиялық жай затты денелердің атомдық жылу сыйымдылықтарының мәндері келтірілген.
Элементтердің қатты күйіндегі атомдық жылу сыйымдылығы
1. 1-кесте
Алюминий, Al
Алмаз, C
Темір, Fe
Алтын, Au
Кадмий, Cd
Кремний, Si
Мыс, Cu
Қалайы, Sn
Платина, Pt
Күміс, Ag
Цинк, Zn
Бор, B
6, 14
1, 35
6, 36
6, 36
6, 11
4, 67
5, 91
6, 63
6, 29
6, 13
6, 10
2, 51
Кестеде келтірілген заттардың көпшілігінің (Al, Fe, Au, Cd т. б. ) атомдық жылу сыйымдылығы 6
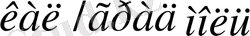 -ға жуық екендігі, яғни олардың атомдары іс жүзінде біріне-бірі тәуелсіз тербелу үшін бөлме температурасы олар үшін жеткілікті жоғары температура болып табылатындығы көрінеді. Бұл заттар үшін Дюлонг пен Пти заңы орындалады. Алмаз, кремний және бордың бөлме температурасындағы атомдық жылу сыйымдылықтары
-ға жуық екендігі, яғни олардың атомдары іс жүзінде біріне-бірі тәуелсіз тербелу үшін бөлме температурасы олар үшін жеткілікті жоғары температура болып табылатындығы көрінеді. Бұл заттар үшін Дюлонг пен Пти заңы орындалады. Алмаз, кремний және бордың бөлме температурасындағы атомдық жылу сыйымдылықтары
6
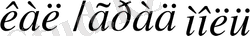 -дан көп кем; бұл осы заттардың кристалдық решеткаларындағы атомдардың бөлме температурасындағы тербелістерін тәуелсіз тербеліс деп есептеуге болмайтындығын білдіреді. Алмаздың 985°С температурадағы атомдық жылу сыйымдылығы 5, 52 болады, яғни болуға тиіс мәні 6 мәніне жуықтайды.
-дан көп кем; бұл осы заттардың кристалдық решеткаларындағы атомдардың бөлме температурасындағы тербелістерін тәуелсіз тербеліс деп есептеуге болмайтындығын білдіреді. Алмаздың 985°С температурадағы атомдық жылу сыйымдылығы 5, 52 болады, яғни болуға тиіс мәні 6 мәніне жуықтайды.
Көптеген химиялық күрделі заттар кристалдарының сипаты иондық сипат болады. Бұл заттардың кристалдарынан жеке молекулаларды бөліп алуға болмайды, ал осы заттар газ күйінде болғанда оларды айырып алуға болады. Кристалдық решеткада осы заттың газ күйіндегі молекулаларының құрамына кірген атомдар ғана иондар түрінде дұрыс алмасып отырады. Бұдан кристалл күйінде осы заттың бір грамм-атомын құрайтын бөлшектердің саны осы заттың бір грамм атомындағы
атомдардың санына
тең болады. Мысалы, газ күйіндегі хлорлы натрийдің бір грамм молекуласындағы NaCl молекулалардың саны Авогадро санына тең болады. Ал қара тікен тұздың кристалында
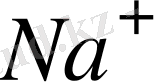 мен
мен
 иондар решетканың түйіндеріне орналасады, бұлардың (
иондар решетканың түйіндеріне орналасады, бұлардың (
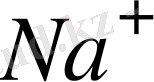 иондар мен
иондар мен
 иондардың) қоса есептегенде жалпы саны 2N-ге тең. Бұрынғыша решеткадағы әрбір ионға
иондардың) қоса есептегенде жалпы саны 2N-ге тең. Бұрынғыша решеткадағы әрбір ионға
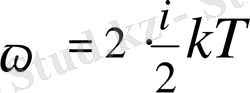 орташа энергия сәйкес келеді деп есептегенде кристалдық тас тұзының молекулалық жылу сыйымдылығы мынаған тең болу керек:
орташа энергия сәйкес келеді деп есептегенде кристалдық тас тұзының молекулалық жылу сыйымдылығы мынаған тең болу керек:
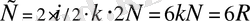 ,
,
немесе шамамен 12
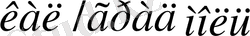 . Решеткадағы атомдар нейтрал (бейтарап) болып біріне-бірі тәуелсіз тербелгенде де осылайша ойлайтын болсақ, ол да болып шығады. Бұдан басқа да екі атомды қосылыстардың қатты күйіндегі молекулалық жылу сыйымдылықтары да шамамен 12
. Решеткадағы атомдар нейтрал (бейтарап) болып біріне-бірі тәуелсіз тербелгенде де осылайша ойлайтын болсақ, ол да болып шығады. Бұдан басқа да екі атомды қосылыстардың қатты күйіндегі молекулалық жылу сыйымдылықтары да шамамен 12
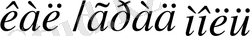 -ға тең болуға тиіс деп айтуға болады.
-ға тең болуға тиіс деп айтуға болады.
Қатты қосылыстардың мольдік жылу сыйымдылықтары
1. 2 кесте
мольдық
жылу
сыйымдылық С
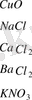
11, 3
12, 1
18, 2
18, 6
24, 1
Сондай-ақ үш атомды қосылыстардың молекулалық жылу сыйымдылығы шамамен 18
 , ал төрт атомды қосылыстардікі - 24
, ал төрт атомды қосылыстардікі - 24
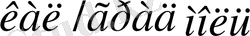 болуға тиіс т. с. с.
болуға тиіс т. с. с.
Сондай-ақ үш атомды қосылыстардың молекулалық жылусыйымдылығы шамамен 18
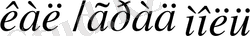 , ал төрт атомды қосылыстардікі - 24
, ал төрт атомды қосылыстардікі - 24
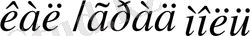 болуға тиіс т. с. с.
болуға тиіс т. с. с.
Бұл қорытынды Джоуль мен Копптың тәжірибе жүзінде тағайындаған заңына дәл келеді; бұл заң бойынша қатты қосылыстардың молекулалық жылу сыйымдылығы осы қосылыстардың құрамына кіретін элементтердің атомдық жылу сыйымдылықтарының қосындысына тең болады.
Джоуль мен Копп заңы бөлшектердің тербелістері біріне-бірі тәуелсіз деп есептелетін жоғары температураларда ғана дұрыс болады.
2-ші кесте Джоуль мен Копп заңы бөлме температурасында бірқатар қосылыстар үшін айтарлықтай дәл келетіндігі көрінеді.
Температура төмендегенде қатты заттардың барлығының да жылу сыйымдылығы төмендейді.
Қатты денелердің жылу сыйымдылығының температураға байланысты төмендеуі график түрінде 1. 1-ші суретте көрсетілген. Температура абсолют нольге қарай жуықтағанда қатты денелердің барлығының да жылу сыйымдылығы нольге жуықтайды. Қатты денелердің жылу сыйымдылықтарының өте төмен температуралардағы өзгерісін кванттық механиканың негізінде ғана түсіндіруге болады.
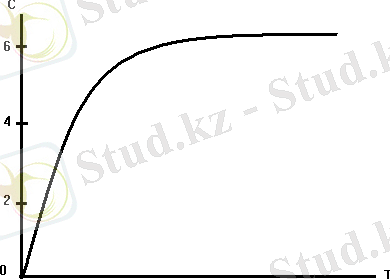
1. 1-сурет
Біз кванттық механика бойынша жеке бөлшектердің энергиясы тек үздік-үздік өзгеретіндігін білеміз.
Кристалдық решеткадағы атомдардың (иондардың) тербеліс энергиясы да осылайша өзгереді. Сонда решеткадағы тербеліп тұратын бөлшектің энергиясының мөлшері
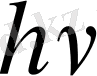 шамаға өзгереді, мұндағы
шамаға өзгереді, мұндағы
 - Планк тұрақтысы, ол 6, 6
- Планк тұрақтысы, ол 6, 6
 эрг секке
тең, ал
эрг секке
тең, ал
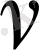 - бөлшектің тербеліс жиілігі. Бір еркіндік дәрежесіне келетін
- бөлшектің тербеліс жиілігі. Бір еркіндік дәрежесіне келетін
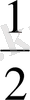
 орташа энергия
орташа энергия
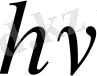 шамаға қарағанда әлдеқайда үлкен болатын температураларда бөлшектің тербеліс энергиясы
Т
температураға байланысты үздіксіз өзгереді деп есептеуге, демек, оған классикалық теорияны қолдануға болады.
шамаға қарағанда әлдеқайда үлкен болатын температураларда бөлшектің тербеліс энергиясы
Т
температураға байланысты үздіксіз өзгереді деп есептеуге, демек, оған классикалық теорияны қолдануға болады.
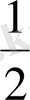
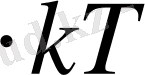 орташа энергия энергияның
орташа энергия энергияның
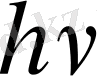 квантымен шамалас болатын төмен температуралардағы есеп кванттық механиканың негізінде жүргізілу керек. Кристалдық решеткадағы бөлшектің тербеліс жиілігі
квантымен шамалас болатын төмен температуралардағы есеп кванттық механиканың негізінде жүргізілу керек. Кристалдық решеткадағы бөлшектің тербеліс жиілігі
 шамасында болады, сонда
шамасында болады, сонда
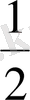
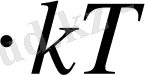 >
>

теңсіздіктен есептеудің классикалық тәсілі мына шартты қанағаттандыратын температуралар үшін дұрыс болатындығы шығады:
Т >
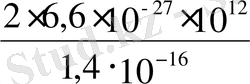 ∙°К
∙°К
 100°К.
100°К.
Сонымен, бөлме температураларында (Т
 300°К) жылу сыйымдылықты есептеуге классикалық тәсілдің жарайтындығы көрінеді, ал - 200°С шамасындағы температураларда жылусыйымдылықты есептеу үшін кванттық теорияны қолдану керек.
300°К) жылу сыйымдылықты есептеуге классикалық тәсілдің жарайтындығы көрінеді, ал - 200°С шамасындағы температураларда жылусыйымдылықты есептеу үшін кванттық теорияны қолдану керек.
Қатты денелер жылу сыйымдылығының кванттық теориясы негіздерін Эйнштейн салған болатын. Сонан кейін Дебай решетканы жасап тұрған бөлшектердің төмен температуралардағы өз ара әсерлерінің ролін еске алған. Дебай жеке бөлшектердің тербелістерін емес тұтас решеткадағы орныққан тербелістерді қарастырған. Ол кристалдық решеткадағы акустикалық толқындарды да қамтитын жиіліктері әр түрлі тұрғын толқындардың орнығатындығын көрсетті.
Кристалдық решетканың осы барлық тербелістерінің энергияларын жинақтап және кванттық механика бойынша олардың температураға тәуелділігін есепке алып, Дебай тәжірибелермен өте жақсы үйлесетін нәтижелерге жеткен. Өте төмен температураларда қатты денелердің жылу сыйымдылығы абсолют температураның үшінші дәрежесіне пропорционал болып өзгереді .
Дебай теориясының артықшылдығы - бұл теория кристалдардағы жылулық тербелістерді олардың акустикалық тербелістерімен байланыстырады.
Совет физигі Л. И. Мандельштам кристалдарда серпімді жылулық толқындардың болуы кристалдан шашырап шығатын жарықтың сипатына әсер ететін болу керек деп көрсетті ( ІІІ томда айтылады) . Л. И. Мандельштамның алдын ала болжап айтқанын совет физигі Е. Ф. Гросс іс жүзінде анықтаған, сонымен, қатты денелерде серпімді жылулық тербелістердің бар екендігі эксперимент жолымен дәлелденген болып табылады.
1. 1. Кристалдың жылу сыйымдылығы
(классикалық теория )
19 ғасырда Дюлонг және Пти қатты денелердің жылу сыйымдылығын зерттей отырып, бөлме температурасына жақын температураларда 1 атомдық кристалдың жылу сыйымдылығын анықтады.
 = 25 Дж/ (моль∙К)
= 25 Дж/ (моль∙К)
Бұл температура өскен сайын жылу сыйымдылығы өсетінің аңғартты. Кешіректе эксперимент нәтижесі көрсеткендей температура күрт төмендегенде жылу сыйымдылығы да төмендейді екен. Абсолют температурада диэлектрлік кристалдарда
 болып, ал металдарда -
болып, ал металдарда -
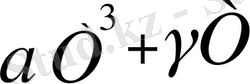 пропорция заңы бойынша өзгереді. (мұндағы
пропорция заңы бойынша өзгереді. (мұндағы
 заттардың қасиетіне байланысты тұрақты шамалар) . 1. 2-ші суретте күміс жылу сыйымдылығының температураға тәжірибе жүзіндегі байланыстылығы көрсетілген. Қатты денелердің жылу сыйымдылығының температуралық қасиеті эксперимент зерттеулер бойынша Дюлонг және Пти заңдарында классикалық бірнеше моделін қарастырамыз. Бір атомдық кристалдық қатты дененің ішкі құрылысының классикалық моделінің жинағын квазитығыз (квазиупругих) күштердің әсерінің кристалдық торлардың түйіндерінде тербеледі деп қарастырамыз. Әр бір атомның тербелісін үштік бос дәрежемен бейнелеуге болады, онда бұл жағдайда қатты денені классикалық осциллятордың жиынтығы ретінде қабылдауға болады. Олардың саны бір мольде Авогадро тұрақтысының үшеуіне көбейтілген. Бұндай мәліметті біле отыра ішкі энергияны табу қиынға соқпайды:
заттардың қасиетіне байланысты тұрақты шамалар) . 1. 2-ші суретте күміс жылу сыйымдылығының температураға тәжірибе жүзіндегі байланыстылығы көрсетілген. Қатты денелердің жылу сыйымдылығының температуралық қасиеті эксперимент зерттеулер бойынша Дюлонг және Пти заңдарында классикалық бірнеше моделін қарастырамыз. Бір атомдық кристалдық қатты дененің ішкі құрылысының классикалық моделінің жинағын квазитығыз (квазиупругих) күштердің әсерінің кристалдық торлардың түйіндерінде тербеледі деп қарастырамыз. Әр бір атомның тербелісін үштік бос дәрежемен бейнелеуге болады, онда бұл жағдайда қатты денені классикалық осциллятордың жиынтығы ретінде қабылдауға болады. Олардың саны бір мольде Авогадро тұрақтысының үшеуіне көбейтілген. Бұндай мәліметті біле отыра ішкі энергияны табу қиынға соқпайды:
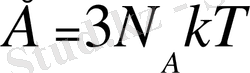
Ал молярлық жылу сыйымдылық
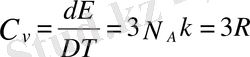 (1. 1)
(1. 1)
Классикалық көзқараста металдың жылу сыйымдылығы әлдеқандай үлкен болу керек. Металдарда электрон өткізгіштер бар, бірақ классикалық тұрғыдан ол үш дәрежелі болып келеді. Егер оның саны атом санына тең деп алсақ (бос бөлшектер сияқты)
 = 1, 5 R т. б. оны 50%-ға ұлғайтады. Шынында да бұл жоқ, Дюлонг және Пти мұны металдарда да ескерілген. Бұл модельдің келісілген температураның жылу сыйымдылыққа байланысы анықталмай отыр, диэлектрик пен металдардың айырмашылығын өте кіші температурада және де Дюлонг пен Пти заңындағы ерекше алмаз, бериллий, бор, кремний, алюминий бөлме температурасында жылу сыйымдылығы 3R -ге жақын өсті. Жылу сыйымдылықтың қатаң теориясын тек кванттық механикалық базада ғана құруға болады.
= 1, 5 R т. б. оны 50%-ға ұлғайтады. Шынында да бұл жоқ, Дюлонг және Пти мұны металдарда да ескерілген. Бұл модельдің келісілген температураның жылу сыйымдылыққа байланысы анықталмай отыр, диэлектрик пен металдардың айырмашылығын өте кіші температурада және де Дюлонг пен Пти заңындағы ерекше алмаз, бериллий, бор, кремний, алюминий бөлме температурасында жылу сыйымдылығы 3R -ге жақын өсті. Жылу сыйымдылықтың қатаң теориясын тек кванттық механикалық базада ғана құруға болады.

1. 2-сурет
Өткен ХХ ғасырдың басында В. Нернст бір топ ғалымдармен бірге көптеген қатты денелердің жылу сыйымдылықтарын үлкен температура аралықтарында (соның ішінде абсолют нөл температураға жақын маңайларда) зерттеп өлшеу жұмыстарын кеңінен жүргізді (Нернст Вольтер Фридрих Герман 1864-1941ж неміс физигі және химигі) . Бұл жұмыстардың нәтижесінде барлық қатты денелердің жылу сыйымдылықтары (
 және
және
 ) температура функция екені және абсолют нөл температураға жақын аймақтарда нөлге айналатыны анықталады:
) температура функция екені және абсолют нөл температураға жақын аймақтарда нөлге айналатыны анықталады:
 (
Т
(
Т
 0) =
0) =
 (
Т
(
Т
 0) =0 (1. 2)
0) =0 (1. 2)
Сондай-ақ, тәжірибе нәтижелеріне сәйкес қатты күйдегі химиялық элементтердің мольдік жылу сыйымдылықтары температура жоғарылаған сайын арта түсіп, Дюлонг-Пти заңымен анықталатын өзінің шектік мәніне ұмтылады екен. Мысал ретінде 1. 3-суретте қорғасын, мыс және алмас үшін жылусыйымдылығы мен температура арасындағы байланысты сипаттайтын тәжірибе жүзінде алынған қисықтар келтірілген. Егер қорғасынның жылу сыйымдылығы 6 кал/моль∙К (25 Дж/моль∙К) мәніне 100
К
өзінде-ақ жетіп үлгерсе, ал мыста бұл тек 400
К
, алмаста - 1270
К
(1000°С) ғана байқалады. Тәжірибе көптеген элементтер үшін Дюлонг және Пти заңы кристалдардың балқу температурасының аймағында орындалатынын және жылу сыйымдылығының мәнінің тұрақтылығы көптеген заттар үшін бөлме температураларына дейінгі аралықтарда сақталатынын көрсетіп отыр.
 - нің термодинамикалық өрнегіне байланысты
- нің термодинамикалық өрнегіне байланысты
 =
=
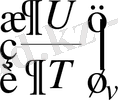 , (1. 3)
, (1. 3)
оны қатты денелер үшін теориялық тұрғыдан анықтау олардың ішкі энергиясының температураға байланыстылығын анықтауға келіп тіреледі. Кристал торының буындарына орналасқан бөлшектердің жалпы потенциал энергиясын Ф арқылы өрнектейік. Бұл шама теріс ( Ф <0) болады да (ол тарту күштеріне негізделген) көлемнің функциясы болып табылады, яғни бөлшектердің ара қашықтықтарына байланысты:
Ф=Ф ( V ) . (1. 4)
Жоғарыда айтқанымыздай, кристалл бөлшектері торбуындарының айналасында тербелмелі қозғалыста болады. Мұны үш координата осьтерінің бойымен болатын тербеліс қорытындысы (қосындысы) ретінде қарастыруға болады. Сонымен кристалдағы әр бөлшектің үш еркіндік дәрежесі бар деп есептеуге болады. Жоғарыда қарастырған молекулалық (атомдық) және металдық кристалдардың бөлшектер тербелісінің энергиясын тауып көрейік.
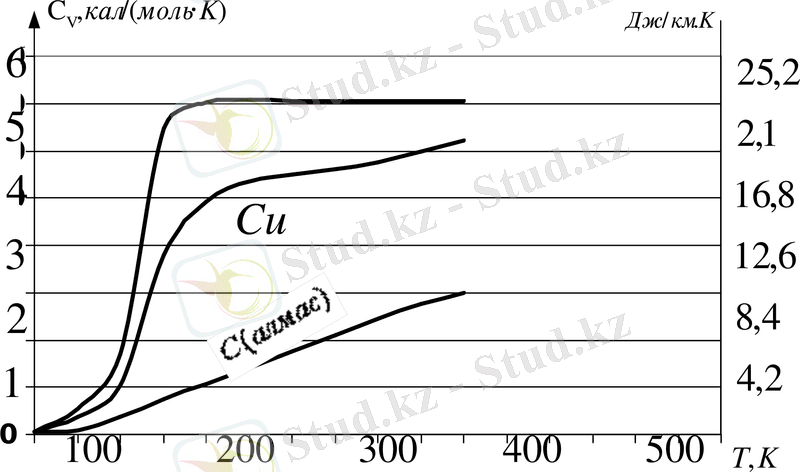
1. 3-сурет
Мұндай кристалдар бөлшектерінің тербелмелі қозғалыс кезінде әрбір еркіндік дәрежесіне орташа энергияның
 мәні сәйкес келеді. Сонда торлардағы әрбір бөлшекке 3
мәні сәйкес келеді. Сонда торлардағы әрбір бөлшекке 3
 тең орташа энергия сәйкес келеді. Бір моль заттың тербеліс энергиясын осы бір бөлшектің орташа энергиясын
тең орташа энергия сәйкес келеді. Бір моль заттың тербеліс энергиясын осы бір бөлшектің орташа энергиясын
 көбейтіп табамыз:
көбейтіп табамыз:
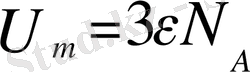 (1. 5)
(1. 5)
Сонымен, (1. 4) және (1. 5) өрнектерінің қосындысы металдық және атомдық кристалдардың ішкі энергиясын сипаттайды:
 (1. 6)
(1. 6)
Мұндағы
Ф
(
V
) >
 және (
Ф
< 0) ескеріп,
U
< 0 екенін айту қажет, міне, сондықтан бөлшектер кристалдық тордың буындарында ұсталып тұрады.
және (
Ф
< 0) ескеріп,
U
< 0 екенін айту қажет, міне, сондықтан бөлшектер кристалдық тордың буындарында ұсталып тұрады.
Кристалдағы тербелмелі қозғалыстағы бөлшектер энергияның еркіндік дәрежелеріне қарай бірдей таралуын сипаттайтын классикалық заңға бағыналы делік. Сонда бір еркіндік дәрежесіне
 тең орташа энергия сәйкес келеді. Осы мәнді (1´) қойып,
тең орташа энергия сәйкес келеді. Осы мәнді (1´) қойып,
 екенін ескеріп, былай жазамыз:
екенін ескеріп, былай жазамыз:
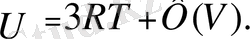 (1. 7)
(1. 7)
Сонда
 =
=
 = 3
R
. (1. 8)
= 3
R
. (1. 8)
Егер
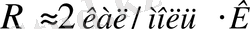 немесе
немесе
 екенін ескерсек, онда классикалық теория негізінде Дюлонг және Пти заңына келеміз. Бірақ классикалық теория қатты денелердің
екенін ескерсек, онда классикалық теория негізінде Дюлонг және Пти заңына келеміз. Бірақ классикалық теория қатты денелердің
 температураға байланыстылығын қарастырмайды. Мұны кванттық теория түсіндіреді.
температураға байланыстылығын қарастырмайды. Мұны кванттық теория түсіндіреді.
1. 2 Қатты денелердің молекула -кинетикалық теориясының негізгі
ұғымдары мен түсініктері.
Біз қатты дене - жер шарының бетінде, қатты денелерден салынған құрылыстарда - үйлерде өмір сүріп жатырмыз. Біздің денеміздің құрамында шамамен 65% су болғанның өзінде (мида 80%) ол қатты денеге жатады. Еңбек құралдары, машиналар да қатты денелерден жасалған. Қатты денелердің қасиеттерін білу тіршілік үшін қажет.
Қатты денелер сұйықтар сияқты өзінің көлемін ғана сақтап қоймайды, сонымен бірге пішінін де сақтайды. Олар негізінен кристалл күйде болады екен.
Қатты денелердің атомдары немесе молекулалары, сұйықтардікіне қарағанда, белгілі бір тепе - теңдік қалыптың маңында тербеліп тұрады. Кей кезде молекулалар өздерінің тепе - теңдік қалпын өзгертеді, бірақ бұл өте сирек болады. Сол себепті қатты денелер көлемін ғана емес, пішінін де сақтайды.
Қатты денелер өздерінің физикалық қасиеттері жағынан бірінен - бірінің өте үлкен айырмашылықтары бар екі топқа, атап айтқанда:
1) кристалл денелер және 2) аморф денелер болып бөлінеді.
Аморфтық денелердің физикалық қасиеттері барлық бағыттар бойынша бірдей болады. Аморфтық денелерге шыны, пластмассалар және т. б. жатады. Аморфтық денелер физикалық қасиеттерінің изотроптылығы оларды құрайтын атомдар мен молекулалардың ретсіз орналасуымен түсіндіріледі.
Атомдары мен молекулалары реттелген, периодты қайталанылатын ішкі құрылымды түзе орналасатын қатты денелер кристалдар деп аталады. Кристалдық денелердің қасиеттері әртүрлі бағыттарда бірдей емес.
Кристалдардың бұл қасиетін анизатроптық деп атайды. Мысалы, кристалл дененің жылулық ұлғаю коэффиценті әр түрлі бағытта түрліше болады; кристалдардың механикалық, оптикалық және электрлік қасиеттері әр түрлі бағытта бірдей болмайды. Кристалдың өзіне тән сыртқы белгісі - оның геометриялық формасының дұрыс болатындығы. Терезе шынысының бетіне су қатқанда байқалатын мұз кристалдарының геометриялық дұрыс формалары жалпыға белгілі. Кристалдардың жан - жағы айнадай жазық болып келеді, ол жазық жақтар бірімен - бірі түзу қырлар және үшкір бұрыштар жасап қиылысады. Әдетте жақтар біріне қарағанда бірі симметриялы болып орналасады.
Кристалдың жазықтары белгілі бір бағытта орналасады, сындырғанда олар көбінесе осы жазықтардың бойымен жарылады. Мысалы, тас тұзының кристалдары ұрғанда өз ара перпендикуляр жазықтықтардың бойымен жарылып сынады, сонда тас тұзының кесектері параллелипипед формалы болады. Ал аморф денелердің сынған жерлері ойлы - қырлы болады; жарылып сынған шыны ұсақтарының белгілі бір формасы болмайды.
Кристалл денелер монокристалдар және поликристалдар болып екіге бөлінеді. Монокристалдың басты ерекшелігі оның бүкіл көлемінде ішкі құрылымының периодты қайталануы болып табылады. Поликристалл бейберекет орналасқан кіші кристалдар жиынтығынан тұрады. Табиғатта кездесетін қатты денелердің басым көпшілігі - тас, құм, металдар, тұздар және т. б. поликристалдар болып табылады. Поликристалл дененің әрбір кіші монокристалы анизотропты, ал поликристал дене изотропты. Кристалдарды құрайтын бөлшектердің кеңістікте дұрыс кристалдық тор түзетіндігі - тәжірибеде анықталған. Кристалдық тор деп түйіндерінде кристалды құрайтын бөлшектер орналасатын кеңістіктік торды айтады. Кристалдар табандарында тек дұрыс үшбұрыш, квадрат, параллелограм және алтыбұрыш жататын әр түрлі призмалар мен пирамиданың пішінінде болады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz