Бір еркіндік дәрежелі механикалық жүйелердің еркін және гармониялық тербелістері: теория, сөну және эксперименттік зерттеу


Мазмұны
Кіріспе
1. Бір еркіндік дәрежелі жүйенің еркін тербелісі
1. 1. Еркіндік дәрежесі бірге жүйенің еркін тербелістері туралы жалпы мәліметтер
1. 2. Еркін тербелістердің негізгі I.
сипаттамалары
1. 3. Кедергі күшінің бір еркіндік дәрежелі жүйедегі еркін тербелістерге әсері
1. 4. Еркін тербелістер. Серіппенің тербелісі
II. Арнайы бөлім
2. 1. Гармониялық тербелістер
2. 1. 1. Гармониялық тербелістер туралы жалпы мәліметтер
2. 1. 2. Гармониялық осциллятордың энергиясы
2. 1. 3. Гармониялық тербелістердің шеңбер бойымен бір қалыпты қозғалыспен байланысы
2. 1. 4. Екі гармониялық тербелістерді қосу
2. 1. 5. Лиссажу фигуралары
2. 1. 6. Фазалар ығысуы
2. 1. 7. Автотербелістерге сипаттама
2. 1. 8. Байланысқан жүйелер тербелістерін зерттеу
2. 2. Механикалық тербелістер
2. 2. 1. Бұралмалы тербелістер
2. 2. 2. Маятник және оның тербелісінің кинематикасы
2. 2. 3. Өшпелі гармониялық тербелістер
2. 2. 4. Өспелі тербелістер
2. 2. 5. Еріксіз тербелістер, резонанс
2. 2. 6. Резонанс құбылысына үйкелістің әсері
III. Эксперименттік бөлім
3. Еркін тербелістер қасиеттерін зерттеу
3. 1. Еркін тербелістер қасиеттерін зерттеудің әдістемесі
3. 2. Зерттеулердің есептеу нәтижелері
3. 3. Зерттеу нәтижелерін талдау
Пайдаланылған әдебиеттер
Кіріспе
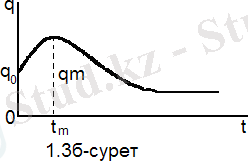
Тербеліс өзінің көп түрлігімен қазіргі техникада үлкен роль атқарады. Тербеліс кездеспейтін техниканың саласын көрсету қиын, сонымен қатар табиғат құбылыстарын біз кеңінен және тереңірек зерттеген сайын жаңа тербелмелі процестер пайда болуда.
Қазіргі заманғы техниканың көптеген салалары тербелмелі құбылыстарға негізделгенін ескерсек, тербелмелі процесстердің маңыздылығын зерттеудің қажеттігі өздігінен туындайды.
Жұмыстың өзектілігі: Физика мен техниканың бірқатар салалары мен біздің планетамыздың тіршілігі түгелдей тербелмелі құбылыстарға негізделгенін айтсақ артық болмайды. Мысалы, ұшатын аппараттар мен кемелердің элементтерінің вибрациясы, музыкалық аспаптардың шектері, телефонның мембранасы, дыбыс зорайтқыштың диффузорлары, іштен жану двигателінің поршені, жер сілкіну, судың қайтуы мен тасуы т. б.
Тербелістің адам өмірінде де атқаратын маңызы зор. Жүректің соғуы, дыбыс желбезегінің дірілі - тербелмелі қозғалыс мысалдары болып табылады.
Тербеліс табиғаты сан қырлы болғандықтан, кейде оның залалды жақтарын ескеріп оны болдырмауға тырысу қажет. Есепке алынбаған тербелістер күрделі техникалық құбылыстарды қиратып зиян келтіреді. Осының бәрі тербелісті жан - жақты зерттеуді қажет етеді.
Қазіргі заманда физика мен техника саласында кездесетін механикалық және электромагниттік тербелістерді физикалық қасиеттері мен байқалуы бойынша біртекті бірдей процесс деп қарастырған дұрыс.
Қайтарушы күштен пайда болған тербелістерді серпімді тербелістер деп атайды. Серіппеге ілінген жүктің тербелісі, рессорлы вагонның, тартылған ішек, кеменің тербелісі - барлығы серпімді тербелістерге жатады.
Мысалы серіппеге ілінген дененің тербелісін қарастырсақ, бұл жағдайда деформация энергиясы тек серіппеде бар деп санауға болады. Себебі дененің деформациясын есепке алмаса да болады. Егер дененің массасы серіппенің массасымен салыстырғанда үлкен болса, онда кинетикалық энергия тек денеде бар деп есептейміз. Ал серіппенің массасын есепке алмаймыз. Осылайша кинетикалық энергияның потенциалдыққа және кері ауысуы, сонымен қатар энергияның денедегі серіппеге және кері ауысуы болып табылады.
Осы пружиналар үшін үлкен массалы дене алып, тербелістің жиілігінің төмендейтініне көз жеткізуге болады. Барлық жағдайда серпімді тербелістер жүйесіндегі массаның өсуі тербелістің тоқталуына, олардың периодының өсуіне алып келеді.
Жұмыстың мақсаты: Бұл жұмыста бір еркіндік дәрежесі бар механикалық жүйенің тербеліс теңдеулеріне талдау жасау, тербелістің сөну дәрежесінің жүйенің қатаңдығы мен демпферлік қасиеттеріне тәуелділігі қарастырылады. Жүйенің қатаңдығын есепке алу үшін маятниктің стерженіне қосымша бекітілген серпімді серіппелер алынған. Серіппенің қатаңдығы алдын ала статикалық әдіспен анықталады.
І ТЕРБЕЛМЕЛІ ҚОЗҒАЛЫСТАР КИНЕМАТИКАСЫ МЕН ДИНАМИКАСЫ
- Тербелмелі қозғалыстың теңдеуін қорытып шығару
Тербелістер физикасының практикалық маңызы өте зор. Ол машиналар мен механизмдердің вибрациясын зерттейді.
Тербеліп тұрған дене басқа денелермен байланыста болып, тербелмелі жүйе құрайды. Барлық тербелмелі жүйеге тән ортақ қасиеттер болады:
а) әрбір тербелмелі жүйенің орнықтылық тепе - теңдік жүйелері болады.
б) тербелмелі жүйе орнықтылық тепе - теңдік күйіне шығарылғаннан кейін оны орнықтылық күйге қайтаратын күш пайда болады.
в) орнықтылық күйге қайтып келген тербелмелі жүйе бірден тоқтамайды.
Мұнда ең алдымен, сандық сипаты тұрғысынан тербелмелі қозғалыстың динамика заңдары негізінде жүйеге асырылатындығын ұғыну керек. Осы тұрғыдан гармониялық осциллятор ұғымын және мысал ретінде серіппелі, физикалық, математикалық маятниктер тербелістерінің бір - бірінен ешқандай айырмашылықтарының жоқ екендігін көрсетіп, оның математикалық формулаларын қорыту негізінде дәлелдеу қажет.
Мынадай дифференциялдық теңдеу
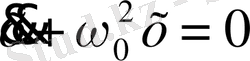 (1)
(1)
бойынша тербелетін система гармониялық осциллятор деп аталады. Гармониялық осциллятор тербелісі периодты қозғалыстың негізгі бір мысалы болып табылады.
Серіппелі маятник серпімді
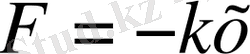 күшінің әсерінен гармониялық тербеліс жасайтын абсолют серпімді серіппеге ілінген жүк. Серіппенің серпімді күші Ньютонның екінші заңы бойынша
күшінің әсерінен гармониялық тербеліс жасайтын абсолют серпімді серіппеге ілінген жүк. Серіппенің серпімді күші Ньютонның екінші заңы бойынша
 . Олай болса маятниктің қозғалыс теңдеуі
. Олай болса маятниктің қозғалыс теңдеуі
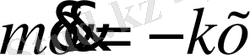
немесе
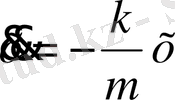 (2)
(2)
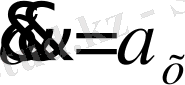 екенін ескерсек, үдеудің тепе - теңдік қалыптан ығысуға тура пропорционал екенін көреміз.
екенін ескерсек, үдеудің тепе - теңдік қалыптан ығысуға тура пропорционал екенін көреміз.
Ауырлық күшінің әсерінен тербелетін созылмайтын, салмақсыз жіпке ілінген массасы m материялдық нүкте математикалық маятник деп аталады. Математикалық маятникті тепе - теңдік қалыптан ауытқытқан кезде ауырлық күшінің тангенциялды құраушысы оны тепе - теңдік қалыпқа келтіруге тырысады. Ньютонның екінші заңы бойынша
(3)
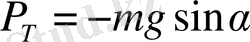
 өте аз шама болғандықтан
өте аз шама болғандықтан
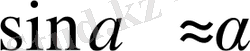 ;
;
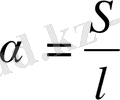 ;
;
 ;
;

(4)
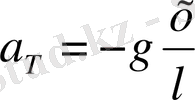 .
.
Математикалық маятник үшін де үдеу тепе - теңдік қалыптан ығысуға (х) пропорционал екендігін көрсету қажет.
Физикалық маятник массалар центрі арқылы өтпейтін горизонталь оське қатысты ауырлық күшінің әсерінен тербелетін қатты дене.
Егер маятник тепе - теңдік қалыптан
 бұрышқа ауытқыса, онда қатты дененің айналмалы қозғалыс динамикасына сәйкес қайтаратын күш моментін мына түрде жазуға болады
бұрышқа ауытқыса, онда қатты дененің айналмалы қозғалыс динамикасына сәйкес қайтаратын күш моментін мына түрде жазуға болады
(5)
Бұрыштық үдеу бұрылу бұрышының екінші ретті туындысы
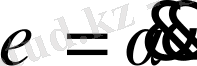 , ал
, ал
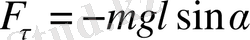 .
.
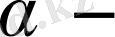 өте аз шама болғандықтан
өте аз шама болғандықтан
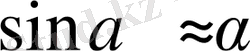 ;
;
 - маятниктің инерция моменті;
- маятниктің инерция моменті;
 - маятниктің массалар центрі мен іліну нүктесінің арақашықтығы.
- маятниктің массалар центрі мен іліну нүктесінің арақашықтығы.
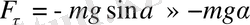 - маятникті тепе - теңдік қалыпқа қайтарушы күш, мұндағы (-)
- маятникті тепе - теңдік қалыпқа қайтарушы күш, мұндағы (-)
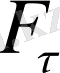 және
және
 бағыттарының қарама - қарсы екендігін көрсетеді.
бағыттарының қарама - қарсы екендігін көрсетеді.
Жоғарыда көрсетілгендерді ескерсек, физикалық маятниктің қозғалыс теңдеуі
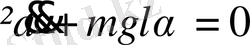
немесе
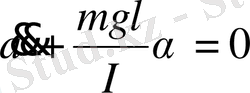
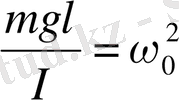 деп белгілесек
деп белгілесек
(6)
Бұл теңдеудің шешімі
(7)
(7) теңдеуден, физикалық маятникті аз α бұрышқа ауытқытса, ол ω 0 циклдік жиілік пен гармониялық тербеліс жасайтынын көреміз.
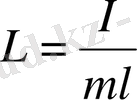 - физикалық маятниктің келтірілген ұзындығы деп аталады. ОС түзуінің бойында жатқан іліну нүктесінен
- физикалық маятниктің келтірілген ұзындығы деп аталады. ОС түзуінің бойында жатқан іліну нүктесінен
 қашықтықтағы О
/
нүктесі тербелу центрі деп аталады.
қашықтықтағы О
/
нүктесі тербелу центрі деп аталады.
1. 2 Маятниктердің тербеліс периоды формуласын қорыту
Егер тербелмелі жүйенің орнықты тепе - теңдік күйінен қандай да бір ауытқуы сыртқы айнымалы әсерге соқтырмайтын болса, онда тербелмелі жүйеде еркін тербелістер пайда болады.
Жоғарыдағы тақырыпта көрсетілген серіппелі маятниктің шарын тепе - теңдік қалпына қарай бағытталған қайтарушы күш әсер етеді. Бұл күш Гук заңы бойынша тепе - теңдік қалпынан ауытқыған дененің ығысуына пропорционал
(8)
Қайтарушы күш тепе - теңдік қалыпқа қарай бағытталғандықтан
 - қарама - қарсы Ньютонның 2 - заңы бойынша
- қарама - қарсы Ньютонның 2 - заңы бойынша
(9)
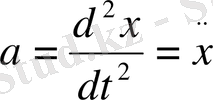 үдеу
үдеу
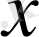 координаттың екінші ретті туындысы
координаттың екінші ретті туындысы
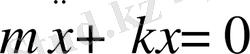 ; (10)
; (10)
немесе
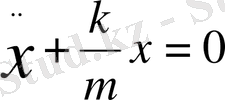 ; (11)
; (11)
(11) теңдеуді
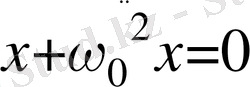 теңдеуімен салыстырсақ
теңдеуімен салыстырсақ
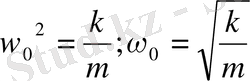 (12)
(12)
(11) теңдеудің шешімі
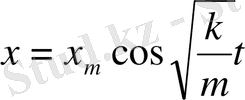 (13)
(13)
немесе
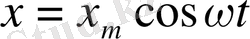 (14)
(14)
Циклдік жиілік ω - мен Т - периодтың арасындағы байланысты ескерсек
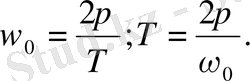
Олай болса, серіппелі маятниктің тербеліс периоды
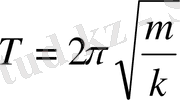 (15)
(15)
формуласымен анықталатындығын көрсету қажет.
Серпімді деформацияланған дененің кинетикалық энергиясы
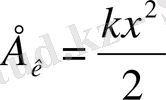 (16)
(16)
Мұндағы k - серіппенің қатаңдық коэффициенті. Қатаңдық коэффициентінің физикалық мағынасын айту қажет. Яғни k - серіппені бірлік ұзындыққа созу үшін қажетті серпімділік күшіне тең.
(15) - теңдіктен серіппенің қатаңдығы артқан сайын тербеліс периодының кемитінін көреміз.
Дәл осы әдіспен математикалық және физикалық маятниктер тербелістерінің теңдеуін қорытуға болады.
Математикалық маятникті тепе - теңдік қалпынан шамалы қашықтыққа ауытқытқанда ауырлық күші мен жүктің керілу күшінің тең әсерлі күші тепе - теңдік қалыпқа қарай бағытталады. Бұл күш
(17)
екінші жағынан

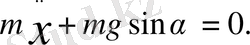
α - ауытқу бұрышы аз болған жағдайда
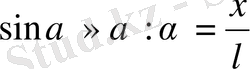 екенін ескерсек
екенін ескерсек
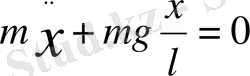
немесе
(18)
(18) теңдікті
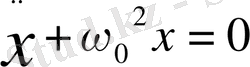 теңдеуімен салыстырсақ
теңдеуімен салыстырсақ
(19)
Тербеліс периоды
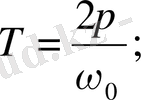
Олай болса, математикалық маятник үшін
(20)
(20) - теңдіктен математикалық маятниктің тербеліс периоды оның ұзындығына тура пропорционал екенін көреміз.
Физикалық маятникті тепе - теңдік қалыптан α - бұрышқа ауытқытқанда айналмалы қозғалыс динамикасының теңдеуіне сәйкес
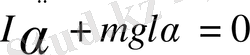
(21)
(21) - теңдікті
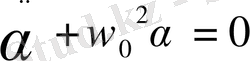 (22)
(22)
теңдігімен салыстырсақ
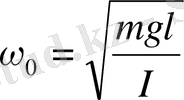 (23)
(23)
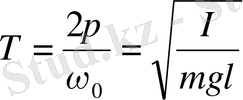 (24)
(24)
Физикалық маятниктің тербеліс периодын анықтайтын формуланы алуға болады.
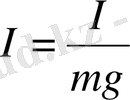 - физикалық маятниктің келтірілген ұзындығы екенін ескерсек
- физикалық маятниктің келтірілген ұзындығы екенін ескерсек
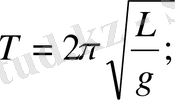
Физикалық маятниктің келтірілген ұзындығы деп тербеліс периоды физикалық маятник периодымен бірдей болып келетін математикалық маятник ұзындығын айтатынын оқушыларға ұғындыру қажет.
- Еркін тербелістердің негізгі сипаттамалары
Еркіндік дәрежесі бірге тең жүйелердің еркін тербелістерінің негізгі сипаттамаларын анықтау үшін осы жүйенің белгілі бір нүктелерінің қозғалысын қарастырамыз. Осы жүйенің қайсыбір
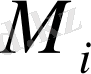 нүктесінің радиус векторын
нүктесінің радиус векторын
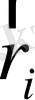 , ал оның декарттық координаталарын
, ал оның декарттық координаталарын
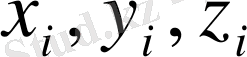 белгілейік.
белгілейік.
Қалыпты жағдайдағы нүктенің радиус векторын
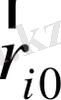 , ал осы жағдайдағы нүктенің декарттық координаталарын
, ал осы жағдайдағы нүктенің декарттық координаталарын
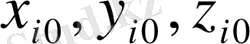 деп белгілейік.
деп белгілейік.
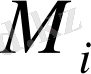 нүктесінің қалыпты жағдайдан ығысуы нүктенің осы жағдайдағы радиус-векторының айырмасымен анықталады.
нүктесінің қалыпты жағдайдан ығысуы нүктенің осы жағдайдағы радиус-векторының айырмасымен анықталады.
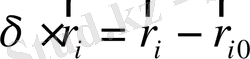
Нүктенің ығысуының декарттық координаталарыңдағы проекциясын
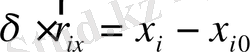
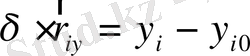 (25)
(25)
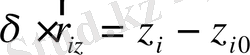
формуласы арқылы табамыз.
Жүйенің нүктесінің координаталары жалпыланған х координаттарының функциясы болады.
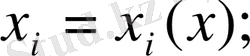
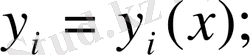
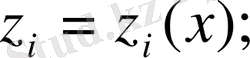
Осы функцияларды х кіші дәрежелі шамасы бойынша ажыратамыз. Бұл ажыратулардың тұрақты мүшелері жүйенің қалыпты жағдайдағы координаттар мәніне тең болады, яғни

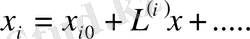
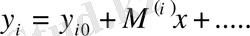 (26)
(26)
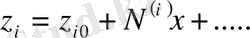
мұндағы:
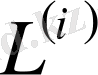 ,
,
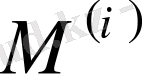 ,
,
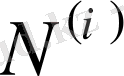 - тұрақты коэффициенттер.
- тұрақты коэффициенттер.
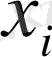 ,
,
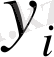 ,
,
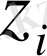 - бастапқы кіші ретті шамаға дейінгі дәлдікпен анықталған нүктенің координаталары. (26) теңдігінен
- бастапқы кіші ретті шамаға дейінгі дәлдікпен анықталған нүктенің координаталары. (26) теңдігінен


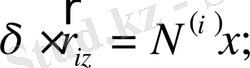 (27)
(27)
Осы формулаларға
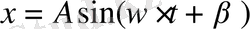 мәнін қойып
мәнін қойып
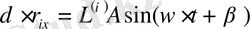
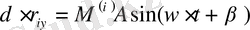
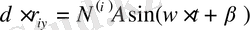
бұдан
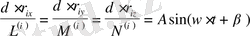
Еркіндік дәрежесі бірге тең жүйелердегі еркін тербелістің сипаттамалары:
1. Жүйенің еркін тербелістері гармониялық тербелістер болады.
- Жүйенің нүктесінің тербеліс амплитудасы яғни тербелістің бастапқы фазасы, бастапқы шарттарға тәуелді болады.
- Жүйенің әр түрлі нүктелерінің амплитудаларының қатынасы бастапқы шарттарға тәуелді емес, себебі бастапқы шарт амплитудаға тек А көбейткіші арқылы әсер етеді. (жүйенің барлық нүктесіне ортақ)
- Жүйенің барлық нүктесі әрқашан бір фазада орналасады, яғни бұл нүктелер бір уақытта өздерінің қалыпты жағдайынан өтеді, бұл нүктенің координаталары бірдей уақытта өздерінің максимум мәніне жетеді.
Еркіндік дәрежесі біргс тең жүйелердің еркін тербелістерінің бұл қасиеттері жуық сызықты дифференциалдық теңдеулерге негізделеді. Егер тербеліс амплитудасы кіші болса, бұл теңдеулер жүйенің нақты қозғалысын дәлірек сипаттайды.
- Кедергі күшінің бір еркіндік дәрежелі жүйедегі еркін тербелістерге әсері
Механикалық жүйенің еркін тербелістері нақты өмірде жүйенің механикалық энергиясының азаюын тудыратын кедергі күшінің бар болған кезінде түзіледі.
Айталық
 жүйесінің әр нүктесіне әсер ететін кедергі күштері жылдамдыққа пропорционал болсын.
жүйесінің әр нүктесіне әсер ететін кедергі күштері жылдамдыққа пропорционал болсын.
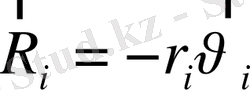
Онда қарастырып отырған бір еркіндік дәрежелі механикалық жүйеде жалпыланған кедергі күшін анықтаймыз.
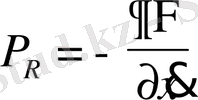
мұндағы Ф - таралу функциясы.
Бір еркіндік дәрежелі жүйенің қозғалысының дифференциалдық теңдеуін алу үшін Лагранж теңдеуін қолданамыз.
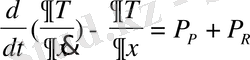
Бір еркіндік дәрежелі жүйе үшін
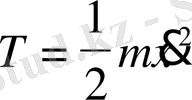
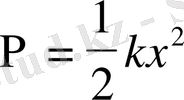
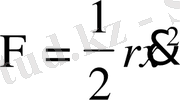
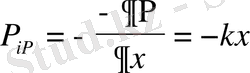
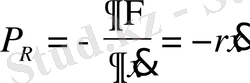
Осы мәндерді Лагранж теңдеуіне қойып
 (28)
(28)
аламыз
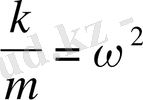
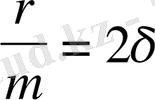
белгілеулерін енгізейік. Сонда (13) теңдеу келесі түрде өрнектеледі.
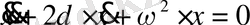 (29)
(29)
Бұл тендеуді тұрақты коэффициентті біртекті сызықты дифференциалдық тендеулерді интегралдау ережесімен интегралдай отырып, характеристикалық теңдеу құрамыз
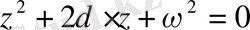
бұл теңдеудің түбірі
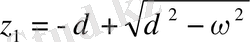

 және
және
 шамаларының қатынастарына байланысты 3 түрлі жағдай болуы мүмкін
шамаларының қатынастарына байланысты 3 түрлі жағдай болуы мүмкін
- яғни аз кедергі кезінде жүйенің қозғалысы өшетін тербелістер түрінде болады
- яғни үлкен кедергі кезінде жүйе апериодты тербелістержасайды.
- кезінде апериодты қозғалыстың шекті жағдайы болады.
Өшетін тербелістер
:
 кезінде (29) теңдеудің жалпы шешімі
кезінде (29) теңдеудің жалпы шешімі
 (30)
(30)
түрінде болады.
Мұнда А және
 бастапқы шарттар бойынша келесі формуламен анықталады
бастапқы шарттар бойынша келесі формуламен анықталады
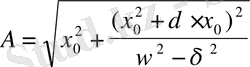
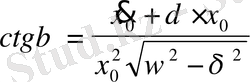 (31)
(31)
(30) теңдеуге сәйкес келетін қозғалыс - тербеліс түрінде болады. Бұл тербелістің графигі (1. 1-суретте) бейнеленген.
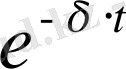 көбейткіші уақыт өткен сайын азаяды. Сондықтан жүйенің тепе-теңдік жағдайынан ауытқуы да азаяды. Өшетін тербелістің периоды
көбейткіші уақыт өткен сайын азаяды. Сондықтан жүйенің тепе-теңдік жағдайынан ауытқуы да азаяды. Өшетін тербелістің периоды
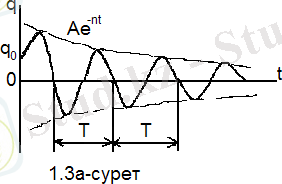
- - сурет
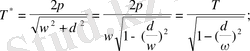 (32)
(32)
Мұндағы
 - кедергі болмаған кездегі жүйенің еркін тербелісінің периоды. Жүйенің тепе - тендік қалпынан ең үлкен екі ауытқуларын бөлетін уақыттың
- кедергі болмаған кездегі жүйенің еркін тербелісінің периоды. Жүйенің тепе - тендік қалпынан ең үлкен екі ауытқуларын бөлетін уақыттың
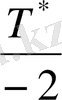 тең, бұдан ол ауытқулардың мәні 1. 2 - сурет.
тең, бұдан ол ауытқулардың мәні 1. 2 - сурет.
1. 2 - сурет
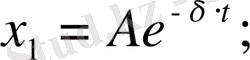

 - абсолют шамасы, жүйенің тепе - теңдік жағдайынан ең үлкен екі ауытқуының қатынасы тербелістің декременті деп аталады. Ол бүкіл тербеліс қозғалысы кезінде өзгермейді.
- абсолют шамасы, жүйенің тепе - теңдік жағдайынан ең үлкен екі ауытқуының қатынасы тербелістің декременті деп аталады. Ол бүкіл тербеліс қозғалысы кезінде өзгермейді.
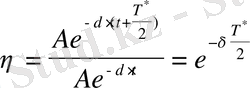 (33)
(33)
осы қатынастың натурал логарифм шамасы тербелістің логарифмдік декременті деп аталады.
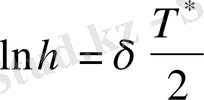 (34)
(34)
Апериодты қозғалыс
:
 кезінде (32) теңдеудің жалпы шешімі
кезінде (32) теңдеудің жалпы шешімі
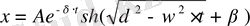 (35)
(35)
түрінде болады.
Бұл апериодты қозғалыстың графигі (1. 1б - суретте) бейнеленген.
Шекті апериодты қозғалыс
:
 кезінде (35) теңдеудің жалпы шешімі
кезінде (35) теңдеудің жалпы шешімі
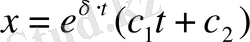 (36)
(36)
түрінде болады.
с 1 және с 2 қозғалыстың бастапқы шарттары бойынша анықталып, (36) теңдеуі
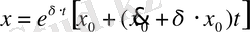 (37)
(37)
түрінде өрнектеледі.
Жүйенің апериодты қозғалысының жалпы сипаттамасы t уақыттың өсуі кезінде жалпыланған координатасының х - тің 0 - ге ұмтылуымен анықталады.
Жылдамдыққа пропорционал кедергі күшінің бір еркіндік дәрежелі жүйенің еркін тербелісіне әсерін қарастыра отырып, төмендегідей қорытындылар жасауға болады.
1. Кедергі күші теріс жұмыс істей отырып, жүйенің энергиясының шексіз азаюына әкеледі, сөйтіп ол жүйенің еркін тербелісінің амплитудасының кішірейюіне әкеліп соқтырады.
2. Аз кедергінің жүйенің еркін тербелісінің жиілігі мен периодына әсері аз, бірақ өте аз кедергінің өзі осы тербелістің тез өшуіне әкеліп соқтырады.
3. Үлкен кедергі кезінде апериодты қозғалыс болады, яғни тербеліс процесі болмайды. [8]
1. 5 Еркін тербелістер. Серіппенің тербелісі
Табиғатта, әсіресе техникада өз - өзінен периодты тербелістер жасайтын денелер мен құрылғылар өте үлкен роль атқарады. Ондай тербелістер еркін тербелістер деп аталады.
Оған, мысал ретінде вертикаль бағытта жіпке ілінген жүктің тербелісін, балалардың әткеншегінің тербелісі, компастың стрелкасының тербелісі т. с. с жатқызуға болады.
Өздігінен тербеліске түсетін мұндай денелер немесе денелер жиыны тербелмелі жүйелер деп аталады. Бұл жүйелердегі тербелістер сыртқы күштің әсерінсіз болатындықтан, олар еркін тербелістер деп аталады.
Механикалық тербелмелі жүйелерден басқа радиотехниканың негізін құрайтын электр тербелістері болатын электромагнитті тербелмелі жүйелер де кездеседі.
Тербеліс дегеніміз бір траекторияның бойымен дененің ерсілі - қарсылы қозғалуы. Қарапайым мысал ретінде серіппенің ұшындағы жүктің қозғалысын қарастыруға болады. Басқа қалған мысалдар осыған ұқсас болғандықтан, бұл мысалды тәптіштеп қарастырамыз.
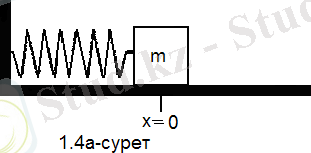
1. 2а - сурет
1. 3 а - сурет
Серіппенің массасын ескермей, серіппе (1. 3а) суреттегідей көлденең орналассын. Серіппенің бір ұшына массасы m жүк бекітілсін. Егер дене серіппені созатындай оңға жылжытсақ немесе оны қысатындай солға жылжытсақ, онда серіппе жүкті тепе - теңдікке түсіруге тырысатын, қайтарушы күшпен әсер етеді. Біздің жүйе үшін Ғ қайтарушы күшті серіппенің

1. 3б-сурет 1. 3 в - сурет
созылу немесе сығылу ара қашықтығына тура пропорционал. (1. 3 б, в сурет)
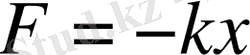
Осы формула серпімділік күші үшін орындалады. «-» минус таңбасы қайтарушы күштің орын ауыстыру бағытына қарама - қарсы екенін көрсетеді.
К - серіппенің қатаңдығы деп аталады. Серіппе қатты болған сайын, "к" тұрақтысы үлкен болады [2] .
Сонымен F қайтарушы күшінің төмендегідей қасиеттері бар:
1-ші, ол жүктің тепе - теңдік қалпынан ығысуына пропорционал;
2-ші, ол әрқашан тепе - теңдік қалпына қарай бағытталған
 [15]
[15]
Егер серіппені
 қашықтыққа созсақ, онда серіппе жүкті оны тепе - теңдікке келтіретіндей орынға әкелуге тырысады. (1. 3 а - сурет) . Бұл күш денеге үдеу беретіндіктен дене тепе - теңдікке үлкен жылдамдықпен келеді. Тепе - теңдік жағдайында денеге әсер ететін күш 0 - ге дейін кемиді де, жылдадық максимал мәнге ие болады (1. 3 б - сурет)
қашықтыққа созсақ, онда серіппе жүкті оны тепе - теңдікке келтіретіндей орынға әкелуге тырысады. (1. 3 а - сурет) . Бұл күш денеге үдеу беретіндіктен дене тепе - теңдікке үлкен жылдамдықпен келеді. Тепе - теңдік жағдайында денеге әсер ететін күш 0 - ге дейін кемиді де, жылдадық максимал мәнге ие болады (1. 3 б - сурет)
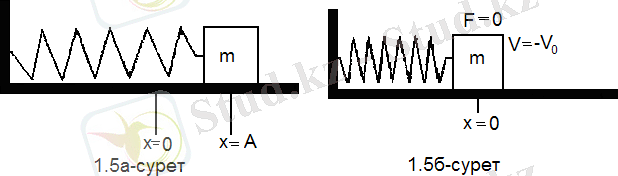
1. 3 а - сурет 1. 3 б - сурет
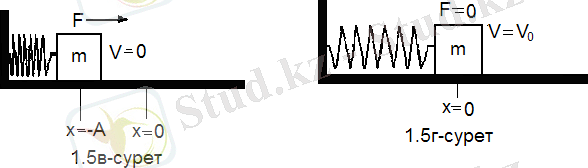 Дене тепе - теңдіктен өтіп, солға жылжығанда серіппе тарапынан әсер ететін күш оның қозғалысын тежейді,
Дене тепе - теңдіктен өтіп, солға жылжығанда серіппе тарапынан әсер ететін күш оның қозғалысын тежейді,
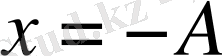 нүктесінде дене бір мезетке тоқтайды (1. 3в-сурет) . Содан соң
нүктесінде дене бір мезетке тоқтайды (1. 3в-сурет) . Содан соң
 нүктесіне келгенше қарама - қарсы бағытта қозғала бастайды. (1. 3г, д - сурет) . Әрі қарай осы процесс қайталанады.
нүктесіне келгенше қарама - қарсы бағытта қозғала бастайды. (1. 3г, д - сурет) . Әрі қарай осы процесс қайталанады.
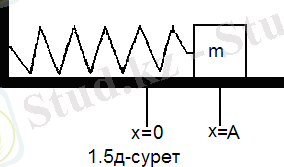 1. 3 в - сурет 1. 3 г - сурет
1. 3 в - сурет 1. 3 г - сурет
1. 3 д - сурет
Тербелісті түсіну үшін бірнеше терминдер енгізейік. Жүктің тепе - теңдік калпынан берілген уақыттағы тұрған орнына дейінгі х қашықтығы - ығысу деп аталады. Тепе - теңдіктен ең үлкен қашықтық - максимал ығысу - амплитуда (А) деп аталады.
Қандай да бір бастапқы нүктеден
 нүктесінен
нүктесінен
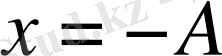 нүктесіне және керісінше
нүктесіне және керісінше
 нүктесіне қарай қозғалыс толық тербеліс деп аталады. Бір толық тербеліске кеткен уақыт - период (Т) деп аталады. 1 сек ішіндегі толық тербелістер саны жиілік
нүктесіне қарай қозғалыс толық тербеліс деп аталады. Бір толық тербеліске кеткен уақыт - период (Т) деп аталады. 1 сек ішіндегі толық тербелістер саны жиілік
 деп аталады. Оны Герцпен өлшейді. (Гц)
деп аталады. Оны Герцпен өлшейді. (Гц)

 (37)
/
(37)
/
Тіке ілінген серіппенің тербелісі көлденең серіппенің тербелісіне ұқсас. [2]
Егер жүк тепе - теңдік қалпынан төмен қарай ығысса қайтарушы күш жоғары қарай бағытталады, жүк жоғары қарай ығысқанда қайтарушы күш төмен бағытталады. [4]
Тіке серіппенің ұзындығы ауырлық күшінің әсерінен тепе - теңдік қалыпта көлденең серіппенікінен ұзынырақ болады. Бірақ, ығысуды тепе - теңдіктің жаңа орнынан бастап есептесе, онда (23) формуласын «к» - ң мәнін өзгертпей сол күйінде қолдануға болады. [2]
Біз қарастырған мысалда қайтарушы күш шынында, өзінің табиғаты бойынша серпімді. Басқа тектегі күштерде де осындай заңдылық байқалуы мүмкін, яғни -
 шамасына тең болуы мүмкін, мұндағы
шамасына тең болуы мүмкін, мұндағы
 -тұрақты оң шама. Табиғатына қарамастан, мұндай күштерді квазисерпімді деп атау келісілген.
-тұрақты оң шама. Табиғатына қарамастан, мұндай күштерді квазисерпімді деп атау келісілген.
Квазисерпімді күш дегеніміз сонымен табиғаты жағынан серпімді емес, бірақ ауытқуы тәуелділігі жағынан серпімді күшке ұқсас болып келген күштер. [12]
ІІ. Гармониялық тербелістер
2. 1 Гармониялық тербелістер туралы жалпы мәліметтер
Қайтарушы күш
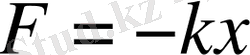 - пен өрнектелетін кез келген тербелмелі жүйе гармониялық тербеліс жасайды. Ондай жүйені көбіне гармониялық осциллятор деп атайды. Табиғатта тербелістер гармониялық немесе соған жақын болады. Ығысудың уакытқа байланысты өзгеруін қарастырайық. Ол үшін Ньютонның ІІ - заңын қолданамыз.
- пен өрнектелетін кез келген тербелмелі жүйе гармониялық тербеліс жасайды. Ондай жүйені көбіне гармониялық осциллятор деп атайды. Табиғатта тербелістер гармониялық немесе соған жақын болады. Ығысудың уакытқа байланысты өзгеруін қарастырайық. Ол үшін Ньютонның ІІ - заңын қолданамыз.

Үдеу
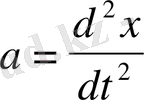 болғандықтан
болғандықтан
 (2. 1)
(2. 1)
Мұны әрі қарай түрлендіріп,
 (2. 2)
(2. 2)
(2. 2) теңдеуі гармониялық осциллятордың қозғалыс теңдеуі деп аталады.
Математикада мұны дифференциалдық оператор кіргендіктен дифференциалдық теңдеу дейді.
 x(t) теңдеуінің жалпы шешімін табуымыз қажет. Теңдеудің шешімін тәжірибеден көреміз.
x(t) теңдеуінің жалпы шешімін табуымыз қажет. Теңдеудің шешімін тәжірибеден көреміз.
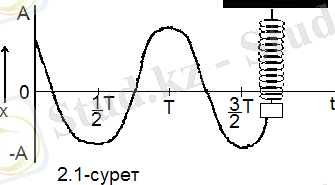
2. 1 - сурет.
2. 1-сурет
Егер тербеліп тұрған жүкке қарандаш жалғап, тұрақты жылдамдықпен оның астына қағаз қойып, тартсақ, онда қарандаш синусоидалық қисықты сызады.
Яғни теңдеудің шешімін
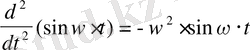
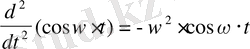
түрінде іздейміз.
мұндағы
 - тұрақты.
- тұрақты.
Теңдеудің шешімі
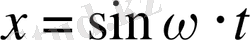

болады.
Жалпы жағдайда теңдеудің шешімі
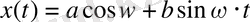
а, в - тұрақтылар.
Осы шешімді 2 рет дифференциалдап,
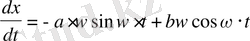
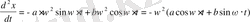
мұны теңдеуге қойып

немесе

Сонымен, біздің тапқан шешіміміздің теңдеуді барлық
 үшін
үшін
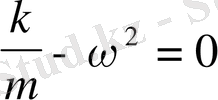 немесе
немесе
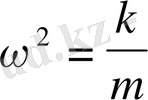 болғаңда қанағаттандырады.
болғаңда қанағаттандырады.
Сонымен теңдеудің шешімі
 (2. 10)
(2. 10)
Реалды физикалық есептерде
a
және
в
тұрақтылары бастапқы шарттармен анықталады. Егер жүкті максимал ығысуға
 апарып, жіберсек, онда қозғалыс
апарып, жіберсек, онда қозғалыс

мұнда
 ,
,
 косинусоида бойынша өтеді.
косинусоида бойынша өтеді.
Eгep t=0 уақытта жүк х=0 нүктесінде болып, оны ұрып оған бастапқы жылдамдықты х - ң оң бағытымен берсек, онда
 ,
,
 деп алуымыз керек. Сонда жалпы шешім
деп алуымыз керек. Сонда жалпы шешім
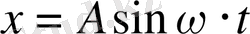 болады.
болады.
(2. 10) теңдеудің шешімін
 (2. 11)
(2. 11)
түрінде де жазуға болады.
(2. 10) пен (2. 11) теңдеуінің бірдейлігі тригонометриялық тепе - теңдіктен шығады.
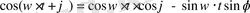
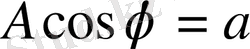

(2. 11) теңдеуі (2. 10) теңдеуіне қарағанда физикалық тұрғыдан қарапайым.
 - шамасы бастапқы фаза деп аталады. Ол
- шамасы бастапқы фаза деп аталады. Ол
 уақыттағы А максимал
уақыттағы А максимал

2. 2 - сурет
ығысудан қалғанын немесе озғанын көрсетеді.
 болғанда
болғанда
 ал
ал
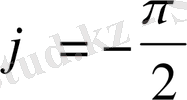 болғанда
болғанда
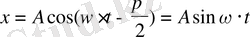
 шамасы x(t) қисығының формуласына әсер етпейді. Ол қандай да бір
шамасы x(t) қисығының формуласына әсер етпейді. Ол қандай да бір
 кезіндегі орнына ғана әсер етеді.
кезіндегі орнына ғана әсер етеді.
Сонымен гармониялық тербелістер синусойдалы болады. Тербеліп тұрған дененің қозғалысы Т периодпен қайталанатындықтан және синус, косинус функциясының периоды
 -гe тең болғандықтан (2. 4) теңдеуінен
-гe тең болғандықтан (2. 4) теңдеуінен
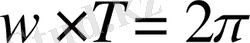 аламыз.
аламыз.
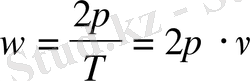
мұндағы
 - тербеліс жиілігі.
- тербеліс жиілігі.
 - циклдік жиілік.
- циклдік жиілік.
Сонымен (2. 4) теңдеуді
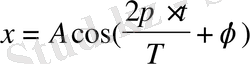 (2. 5)
(2. 5)
немесе
 деп жазуға болады.
деп жазуға болады.
мұндағы
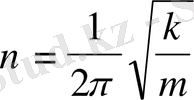 (2. 6)
(2. 6)
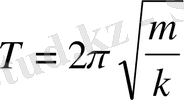
жиілік пен тербеліс периоды амплитудаға байланысты емес.
(2. 6) формуладан масса үлкен болған сайын жиілігі азаятынын, серіппенің қатаңдығы үлкейген сайын, жиілік көбейетінін көреміз. Шынында да массасы үлкен дене инертті, үдеуі аз, ал қатаңдығы үлкен серіппе көп үдеу туғызады.
(2. 5) теңдеуін дифференциалдап, тербелістің жылдамдығы мен үдеуін табуға болады.
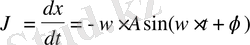 (2. 7)
(2. 7)
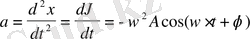 (2. 8)
(2. 8)
Гармониялық осциллятордың жылдамдығы мен үдеуі де синусоидалық заңмен өзгереді. [2]
1. материалдық нүктенің жылдамдығы мен үдеуі, ығысу сияқты, (
 ) және периоды (
) және периоды (
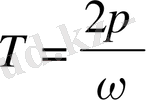 ) бірдей гармониялық тербеліс жасайды.
) бірдей гармониялық тербеліс жасайды.
2. Бұл тербелістердің амплитудалары әр - түрлі:
Ығысу амплитудасы - А;
Жылдамдықтың амплитудасы -
 ;
;
Үдеудің амплитудасы -
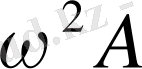 .
.
3. Тербелістердің фазалары да әр түрлі: Жылдамдық тербелісінің фазасы ығысу тербелісінің фазасынан
 - ге озып кетсе; Үдеу тербелісінің фазасынан
- ге озып кетсе; Үдеу тербелісінің фазасынан
 - гe озып кетеді. [5]
- гe озып кетеді. [5]

2. 3 - сурет
2. 3 - сурет
2. 3 - суретте гармониялық осциллятордың ығысу, жылдамдық, үдеуінің
 үшін уақытқа байланысты тәуелділігі көрсетілген.
үшін уақытқа байланысты тәуелділігі көрсетілген.
Жүк х=0 нүктесінде тепе - теңдік күйінен өткенде жылдамдық өзінің
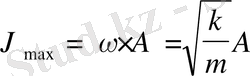
максимал мәніне ие болады. Жылдамдық максимал ығысу
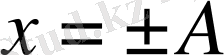 кезінде 0 - ге тең. Үдеудің максимал мәні
кезінде 0 - ге тең. Үдеудің максимал мәні
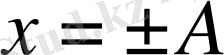
 , ал
, ал
 нүктесінде үдеу 0 - ге тең болады.
нүктесінде үдеу 0 - ге тең болады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz