Скаляр аргументті векторлық функциялар: шек, туынды, дифференциал және өрістер


1 СКАЛЯР АРГУМЕНТТІҢ ВЕКТОР ФУНКЦИЯСЫ
1. 1 Вектордың скаляр аргумент бойынша туындысы және дифференциалы
Физикалық құбылыстарды математикалық жолмен зерттеу қажет болғанда, оларды сандар арқылы өрнектеу үшін кеңістікті арифметикаландыру әдісі жүргізіледі. Бірақ бұл үдеріс, физикалық құбылыстарды зерттеу кезінде қолданылатын шамалар арифметикаландыру әдісіне тәуелсіз (инвариантты) болатындай етіп жүргізілуі қажет. Шамалар көбінесе екі түрлі болады: өзінің сандық мәні арқылы толық сипатталатын - скалярлық шама (ұзындық, көлем, тығыздық, масса, температура т. с. с. ) ; сандық мәні және бағыты арқылы толық сипатталатын - векторлық шама (жылдамдық, үдеу, күш т. с. с) .
Анықтама.
Егер қандай да бір ∆ сандар жиынының әрбір
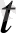 нүктесіне а = a(
нүктесіне а = a(
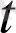 ) векторы сәйкес қойылса, онда Δ жиынында скаляр аргумент
) векторы сәйкес қойылса, онда Δ жиынында скаляр аргумент
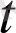 -нің
а (
-нің
а (
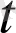 ) вектор-функциясы (немесе векторлық функциясы)
анықталды дейді.
) вектор-функциясы (немесе векторлық функциясы)
анықталды дейді.
Егер а = а (
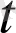 ) вектор-функциясы жататын кеңістіктің қандай да бір, мысалы,
I, j, k
базистік векторлар жүйесін алсақ, онда а векторын келесі векторлардың қосындысы түрінде жазуға болады:
) вектор-функциясы жататын кеңістіктің қандай да бір, мысалы,
I, j, k
базистік векторлар жүйесін алсақ, онда а векторын келесі векторлардың қосындысы түрінде жазуға болады:
A(
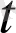 ) = a
x
(
) = a
x
(
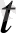 )
i + a
y
(
)
i + a
y
(
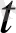 )
j +
a
z
(
)
j +
a
z
(
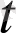 )
k
(1. 1. 1)
)
k
(1. 1. 1)
мұнда a
x
(
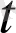 ) . a
y
(
) . a
y
(
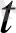 ), a
z
(
), a
z
(
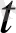 ) арқылы
a
(
) арқылы
a
(
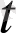 ) векторының сәйкес
і, j, k
векторынапроекциялары (I, j, k базисіндегі координаттары:
a
(
) векторының сәйкес
і, j, k
векторынапроекциялары (I, j, k базисіндегі координаттары:
a
(
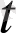 ) = (a
x
(
) = (a
x
(
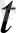 ), a
y
(
), a
y
(
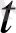 ), a
z
(
), a
z
(
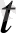 ) ) белгіленген. Сонымен вектор-функцияның берілуі оның координаттары болатын үш скаляр функцияның: a
x
(
) ) белгіленген. Сонымен вектор-функцияның берілуі оның координаттары болатын үш скаляр функцияның: a
x
(
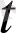 ), a
y
(
), a
y
(
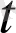 ), a
z
(
), a
z
(
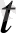 ) берілуімен парапар.
) берілуімен парапар.
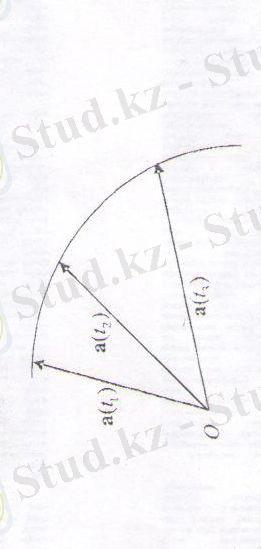 а(
а(
 ) вектор-функцияның басы
О
координаттық бас нүктеден шығады, ал оның ұшы, аргумент
) вектор-функцияның басы
О
координаттық бас нүктеден шығады, ал оның ұшы, аргумент
 -нің мәндеріне сәйкес, қандай да бір нүктелердің
годограф
деп аталатын геометриялық орнын құрайды (1. 1-сурет)
-нің мәндеріне сәйкес, қандай да бір нүктелердің
годограф
деп аталатын геометриялық орнын құрайды (1. 1-сурет)
(1. 1-сурет)
Егер а(
 ) вектор функциясының i, j, k, базисіндегі координаттарын сәйкес x, y, z арқылы белгілесек, онда осы вектор годографының
) вектор функциясының i, j, k, базисіндегі координаттарын сәйкес x, y, z арқылы белгілесек, онда осы вектор годографының
x= a
x
(
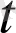 ), y = a
y
(
), y = a
y
(
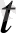 ), z=a
z
(
), z=a
z
(
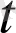 ) (1. 1. 2)
) (1. 1. 2)
түріндегі параметрлік теңдеулерін аламыз. Мысалы,
a(
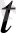 ) =(2
) =(2
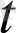 - 1) i +(+1) j+
- 1) i +(+1) j+
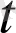 k,
k,
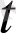 ) вектор-функциясы годографының параметрлік теңдеулері x=2
) вектор-функциясы годографының параметрлік теңдеулері x=2
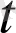 . Бұдан параметр t-ні шығарып тастап, годографтың канондық теңдеуңн аламыз:
. Бұдан параметр t-ні шығарып тастап, годографтың канондық теңдеуңн аламыз:
= .
Егер «параметр
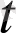 белгілі бір
белгілі бір
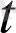 0
нүктесіне ұмтылғанда, а(
0
нүктесіне ұмтылғанда, а(
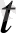 ) вектор-функциясы қандайда бір тұрақты а
0
векторына ұмтылады» деген ұғымды анықтайды.
) вектор-функциясы қандайда бір тұрақты а
0
векторына ұмтылады» деген ұғымды анықтайды.
Анықтама. а(
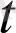 ) вектор-функциясы
) вектор-функциясы
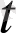 0
нүктесінің қандай да бір маңайында анықталсын, ал а
0
қандай да бір вектор болсын. Егер берілген кез келген оң
саны бойынша 0<
0
нүктесінің қандай да бір маңайында анықталсын, ал а
0
қандай да бір вектор болсын. Егер берілген кез келген оң
саны бойынша 0<
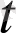 -
-
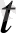 0
<
(
)
теңсіздігін қанағаттандыратын барлық
0
<
(
)
теңсіздігін қанағаттандыратын барлық
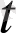 үшін а(
үшін а(
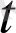 ) -a
0
шарты орындалатын
оң саны табылса, онда тұрақты
а
0
векторын
а
(
) -a
0
шарты орындалатын
оң саны табылса, онда тұрақты
а
0
векторын
а
(
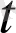 ) вектор функциясының t
0
нүктесіндегі шегі деп атайды және оны өрнегі түрінде жазады.
) вектор функциясының t
0
нүктесіндегі шегі деп атайды және оны өрнегі түрінде жазады.
Анықтамадан және
Анықтама. a
(
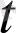 ) вектор-функциясы
) вектор-функциясы
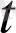 нүктесінің қандайда бір маңайында аныұталсын, ал а қандай да бір вектор болсын. Егер берілген кез келген оң ε саны бойынша 0<
нүктесінің қандайда бір маңайында аныұталсын, ал а қандай да бір вектор болсын. Егер берілген кез келген оң ε саны бойынша 0<
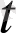 -
-
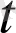 0
<δ(ε) теңсіздігін қанағаттандыратын барлық
0
<δ(ε) теңсіздігін қанағаттандыратын барлық
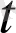 үшін а(
үшін а(
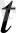 ) - а
0
<ε шарты орындалатын δ(ε) оң саны табылса, онда тұрақты а
0
векторын а(
) - а
0
<ε шарты орындалатын δ(ε) оң саны табылса, онда тұрақты а
0
векторын а(
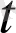 ) вектор-функциясы
) вектор-функциясы
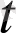 0
нүктесіндегі шегі деп атайды және оны
өрнегі түрінде жазады.
0
нүктесіндегі шегі деп атайды және оны
өрнегі түрінде жазады.
Анықтамадан
және
теңдіктерінің парапар екенін көреміз. Бұл геометриялық түрде
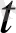 ұмтылғанда а(
ұмтылғанда а(
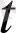 ) вектор-функциясының ұшы тұрақты а
0
векторының ұшына «мейлінше жақын» келетінін көрсетеді (олардың бастары координаттардың бас нүктесінде түйіскен) .
) вектор-функциясының ұшы тұрақты а
0
векторының ұшына «мейлінше жақын» келетінін көрсетеді (олардың бастары координаттардың бас нүктесінде түйіскен) .
Сонымен бірге
теңдігін а(
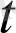 ) = a + α(
) = a + α(
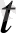 ) теңдігі арқылы да жазуға болады. (мұндағы α(t) - ақырсыз кішкене вектор-функция, яғни
) теңдігі арқылы да жазуға болады. (мұндағы α(t) - ақырсыз кішкене вектор-функция, яғни
Егерa 0 болса, онда орындалуы үшін.
теңсіздіктерінің орындалуы қажетті және жеткілікті. Бұл тұжырымды келесі теңдікті пайдаланып дәлелдеуге болады.
Векторлық алгебра теориясындағы векторға қолданылатын амалдарды ескерсек, функцияның шегіне қатысты математикалық анализ курсынан белгілі қасиеттер вектор-функцияның шегі үшін де орындалады. Мысалы:
(1. 1. 3)
теңдігінің орындалатынын көрсетейік. Бұл, егер (4) теңдігінің оң жағындағы шектер бар болса, онда оның сол жағындағы шек те бар және (4) теңдігі орындалады деген сөз. Алдымен, егер ал q(1) вектор-функциясы t 0 нүктесінің қандайда бір маңайында шенелген болса онда
теңдігінің орындалатынын атап өтеміз. Бұл теңдікті келесі теңсіздікті пайдаланып дәлелдеуге болады.
Енді
(t) =b,
(
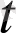 ) =c деп алайық. Онда
және
ақырсыз кішкене вектор-функциялар. яғни
теңсіздіктер орындалады. Бұдан ((5) -ті қараңыз)
) =c деп алайық. Онда
және
ақырсыз кішкене вектор-функциялар. яғни
теңсіздіктер орындалады. Бұдан ((5) -ті қараңыз)
аламыз. Ал бұдан b теңсіздігін пайдаланып, яғни, b ақырсыз кішкене вектор-функция екенін көреміз. Одан әрі қарай,
теңдігінен
немесе
(
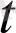 ) теңдікке келеміз.
) теңдікке келеміз.
Енді шектердің қасиеттерін пайдаланып, келесі теңдікті жаза аламыз. Бұл а(
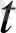 ) [вектор-функцияның шегін оның
(
) [вектор-функцияның шегін оның
(
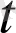 )
, (
)
, (
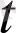 ), a(
), a(
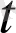 ) проекциясының шегі арқылы табуға болатынын білдіреді.
) проекциясының шегі арқылы табуға болатынын білдіреді.
Анықтама. а(t)
вектор-функциясы аргументтің
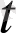 =
=
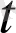 нүктесінде және оның қандайда бір маңайындағы нүктелерде анықталсын. Егер
шегі бар және
нүктесінде және оның қандайда бір маңайындағы нүктелерде анықталсын. Егер
шегі бар және
=a( (1. 1. 4)
теңдігі орындалса, онда а(
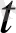 ) вектор-функциясы
) вектор-функциясы
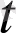 =
нүктесінде
үзіліссіз
деп аталады.
=
нүктесінде
үзіліссіз
деп аталады.
Егер ∆a(
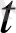 ) =a(
) =a(
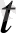 ) - a(
белгілеулерін енгізсек, онда
теңдігін
немесе
) - a(
белгілеулерін енгізсек, онда
теңдігін
немесе
=0 (7)
арқылы жазуға болады. Олай болса, (7) теңсіздіктің орындалуы а(
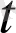 ) вектор-функциясы
) вектор-функциясы
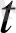 =
=
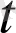 мәнінде үзіліссіз болатынын қөрсетеді.
мәнінде үзіліссіз болатынын қөрсетеді.
(6) теңдікті (3) теңдіктер түрінде жаза отырып,
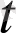 =
=
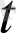 нүктесінде
нүктесінде
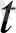 =(a(t), a(
=(a(t), a(
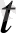 ), a(
), a(
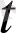 ) ) вектор-функциясы үзіліссіз болуы үшін, осы нүктеде a(
) ) вектор-функциясы үзіліссіз болуы үшін, осы нүктеде a(
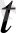 ), a(
), a(
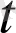 ),
),
a(
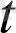 ) функцияларының үзіліссіз болуы қажет және жеткілікті екенін көреміз,
) функцияларының үзіліссіз болуы қажет және жеткілікті екенін көреміз,
Скаляр аргументтер тәуелді үзіліссіз вектор-функцияның годографы - үзіліссіз қисық, сонымен бірге үзіліссіз вектор-функциялардың қосындысы, айырымы, скалярлық және векторлық көбейтінділері, үзіліссіз вектор-функцияның үзіліссіз скаляр функцияға көбейтіндісінің үзіліссіз функциялар ᵗболатынын көруге болады.
(7) теңдігі және
теңсіздігін пайдаланып, келесі теңдікті жаза аламыз
. Ал бұл
вектор функциясының үзіліссіздігінен оның
модулінің үзіліссіздігі шығатынын көрсетеді. Бірақ бұған кері тұжырым дұрыс емес. Мысалы, келесі вектор-функция
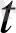 =1 нүктесінде үзілісті:
=1 нүктесінде үзілісті:
(тексеріңіз), бірақ оның модулі тұрақты, 1-ге тең: a(
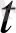 ) =1, ал тұрақты шама - үзіліссіз.
) =1, ал тұрақты шама - үзіліссіз.
Бұдан әрі жаңылыс тудырмаса, «вектор-функцияны» қысқаша «вектор» деп те атауымыз мүмкін.
а(t)
вектор функциясы
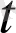 нүктесінің қандай да бір U(
нүктесінің қандай да бір U(
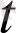 ) маңайдан алынған
) маңайдан алынған
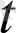 мәніне a(
мәніне a(
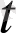 ) векторы сәйкес келеді, ал аргументтің осы
) векторы сәйкес келеді, ал аргументтің осы
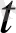 мәніне
мәніне
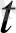 мәніне
мәніне
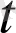 +∆
+∆
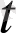 саны U(
саны U(
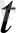 ) маңайда жататындай ∆
) маңайда жататындай ∆
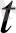 өсімшесін қоссақ, оған
өсімшесін қоссақ, оған
а(
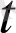 +∆
+∆
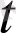 ) векторы сәйкес келеді. а(
) векторы сәйкес келеді. а(
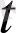 ) вектор-функциясының
) вектор-функциясының
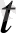 нүктесіне (
нүктесіне (
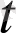 -бекітілген) сәйкес өсімшесі деп аталатын ∆а(
-бекітілген) сәйкес өсімшесі деп аталатын ∆а(
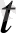 ) =a(
) =a(
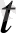 +∆
+∆
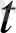 ) ˗a(
) ˗a(
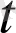 ) айырымы скаляр айнымал ∆
) айырымы скаляр айнымал ∆
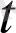 -нің вектор-функциясы болады. (16 бет, 1. 2-суретте: ∆а(
-нің вектор-функциясы болады. (16 бет, 1. 2-суретте: ∆а(
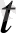 ) =MN) .
) =MN) .
Анықтама.
Егер ∆
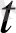 →0 ұмтылғанда
→0 ұмтылғанда
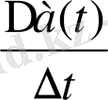 қатынасының шегі бар болса. онда ол а(
қатынасының шегі бар болса. онда ол а(
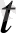 ) вектор-функцияның
) вектор-функцияның
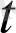 нүктедегі туындысы деп аталады да, а(
нүктедегі туындысы деп аталады да, а(
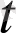 ), a(
), a(
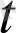 ),
),
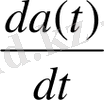 cимволдарының беруімен белгіленеді:
cимволдарының беруімен белгіленеді:
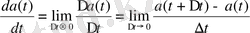 . (1. 1. 5)
. (1. 1. 5)
a(
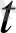 ) =(
) =(
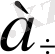 (
(
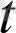 ), a(
), a(
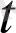 ), a(
), a(
 ) ) вектор туындысындағы анықтамасындағы (8) теңдікті (3) теңдіктер түрінде жазсақ,
) ) вектор туындысындағы анықтамасындағы (8) теңдікті (3) теңдіктер түрінде жазсақ,
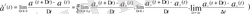
яғни, а(
 ) =(a (
) =(a (
 ), a (
), a (
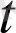 ), a(
), a(
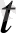 ) )
) )
теңдігін аламыз. Ал оның модулі:
ǀа(t) ǀ=
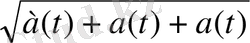 (1. 1. 6)
(1. 1. 6)
Анықтама. Егер t нүктесінің қандайда бір маңайында анықталған а(t) вектор-функциясының ∆a(
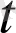 ) =b(
) =b(
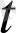 ) ∆
) ∆
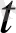 +0(∆
+0(∆
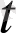 ), (1. 1. 7)
), (1. 1. 7)
(мұндағы b(
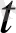 ) тек
) тек
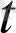 нүктесіне тәуелді қандай да бір вектор; ал
нүктесіне тәуелді қандай да бір вектор; ал
о(∆
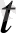 ) қосылғышы
) қосылғышы
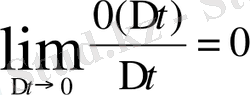 шартын қанағаттандыратын вектор) теңдігі түрінде өрнектеуге болса, онда а(
шартын қанағаттандыратын вектор) теңдігі түрінде өрнектеуге болса, онда а(
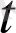 ) вектор-функциясын
) вектор-функциясын
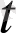 нүктесінде
дифферациалданады
дейді және а(
нүктесінде
дифферациалданады
дейді және а(
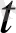 ) вектор-функциясының
) вектор-функциясының
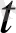 нүктедегі дифференциалы деп аталады да, da(
нүктедегі дифференциалы деп аталады да, da(
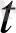 ) символымен белгіленеді: da(
) символымен белгіленеді: da(
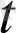 ) =b(
) =b(
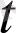 ) ∆
) ∆
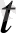 .
.
Математикалық анализ курсында көрсетілгендей, а(
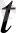 ) вектор-функцияның берілген нүктеде дифференциалдануы мен оның осы нүктедегі ақырлы туындысының бар болуы парапар ұғымдар және а(
) вектор-функцияның берілген нүктеде дифференциалдануы мен оның осы нүктедегі ақырлы туындысының бар болуы парапар ұғымдар және а(
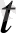 ) =b(
) =b(
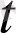 ) екенін көз жеткізуге болады.
) екенін көз жеткізуге болады.
Тәуелсіз айнымал
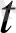 үшін, анықтама бойынша d
үшін, анықтама бойынша d
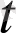 =∆
=∆
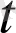 деп аламыз. Онда алдынғы айтылғандарды ескере отырып, da(
деп аламыз. Онда алдынғы айтылғандарды ескере отырып, da(
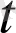 ) =a(
) =a(
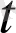 ) dt теңдігін жаза аламыз Ал бұдан (9) теңдікті ескеріп, а(
) dt теңдігін жаза аламыз Ал бұдан (9) теңдікті ескеріп, а(
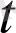 ) =
) =
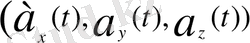 векторының дифференциалы мен оның модулің жаза аламыз:
векторының дифференциалы мен оның модулің жаза аламыз:
da(t) =d
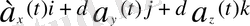 (1. 1. 8)
(1. 1. 8)
│da(t) │=
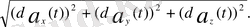 (1. 1. 9)
(1. 1. 9)
Келесі вектор-функцияларды дифференциалдау формулаларын скаляр функцияны дифференциалдау формулалары сияқты дәлелдеуге болады(жаттығу ретінде тексеріңіз) :
1. (
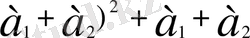 2.
2.
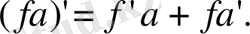
3.
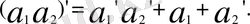 4.
4.
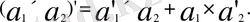
Келесі da(
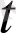 ) мен d│a(
) мен d│a(
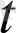 ) │дифференциалдарының арақатысын сипаттайтын теңдік жиі қолданылады.
) │дифференциалдарының арақатысын сипаттайтын теңдік жиі қолданылады.
d│a(
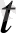 ) │=
) │=
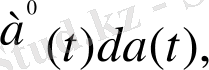 (1. 1. 10)
(1. 1. 10)
мұндағы
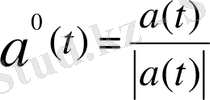 берілген a(
берілген a(
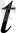 ) векторының бірлік векторы.
) векторының бірлік векторы.
Шынында да, белгілі
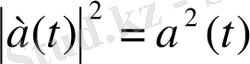 теңдігінің екі жағын
теңдігінің екі жағын
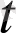 бойынша дифференциалдасақ,
бойынша дифференциалдасақ,
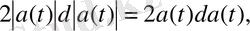 ал бұдан (14) теңдік шығады.
ал бұдан (14) теңдік шығады.
Назар аударыңыз! d│a(t) │шамасы
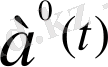 мен da(t) векторының скаляр көбейтіндісіне тең, демек ол - da(t) векторының
мен da(t) векторының скаляр көбейтіндісіне тең, демек ол - da(t) векторының
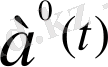 векторына проекциясы.
векторына проекциясы.
1. 2 ВЕКТОР ТУЫНДЫСЫНЫҢ ГЕОМЕТРИЯЛЫҚ ЖӘНЕ
МЕХАНИКАЛЫҚ МАҒЫНАЛАРЫ
a
(t) векторының
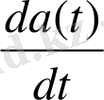 туындысына геометриялық мағынасын қарастырайық.
туындысына геометриялық мағынасын қарастырайық.
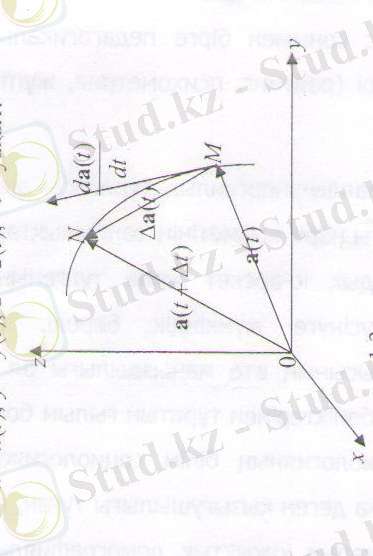
∆a(t) =a(
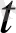 +∆
+∆
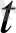 ) - a(
) - a(
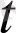 ) мен
) мен
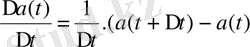 векторы а(
векторы а(
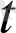 ) векторының годографасы а(
) векторының годографасы а(
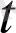 ) мен a(
) мен a(
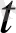 +∆
+∆
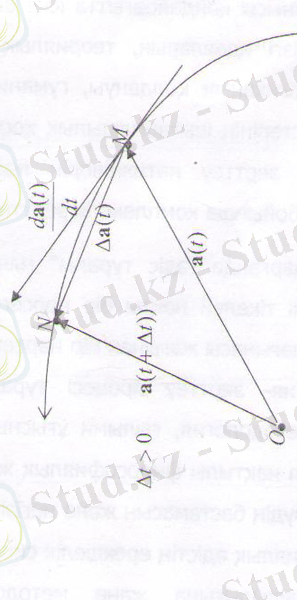
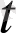 ) векторларының ұштары арқылы өтетін MN қиюшыда орналасады. (1. 2. 1-сурет ) . Егер ∆
) векторларының ұштары арқылы өтетін MN қиюшыда орналасады. (1. 2. 1-сурет ) . Егер ∆
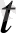 >0 болса, онда ол векторлар годографтың t аргументінің өсуі бойынша анықталған бағыты жағына қарай бағытталады. Егер ∆
>0 болса, онда ол векторлар годографтың t аргументінің өсуі бойынша анықталған бағыты жағына қарай бағытталады. Егер ∆
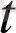 <0 болса, онда ∆a(
<0 болса, онда ∆a(
 ) векторы бағытын қарама-қарсыға өзгертеді, яғни ол годографтың t аргументінің кемуі бойынша анықталған бағыты жағына қарай бағытталады, ал ∆
) векторы бағытын қарама-қарсыға өзгертеді, яғни ол годографтың t аргументінің кемуі бойынша анықталған бағыты жағына қарай бағытталады, ал ∆
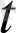 <0 болғандықтан
<0 болғандықтан
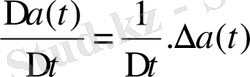 векторы ∆a(
векторы ∆a(
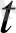 ) векторына қарама-қарсы яғни бұрынғыдай, годографтың
) векторына қарама-қарсы яғни бұрынғыдай, годографтың
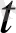 аргументінің
аргументінің
 өсуі бойынша анықталған бағыты жағына қарай бағытталады.
өсуі бойынша анықталған бағыты жағына қарай бағытталады.
(1. 2. 1-сурет)
Годогрофтың M нүктесіндегі жанама (бар болса) MN қиюшының ∆
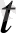 →0 ұмтылғандағы шектік жағдайы екенін ескеріп, теңдік бойынша келесі тұжырымға келеміз:
→0 ұмтылғандағы шектік жағдайы екенін ескеріп, теңдік бойынша келесі тұжырымға келеміз:
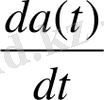 туындысы -
a(t) векторынын ұшы арқылы жүргізілген годограф жанамасында орналасқан және годографтың
туындысы -
a(t) векторынын ұшы арқылы жүргізілген годограф жанамасында орналасқан және годографтың
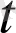 аргументінің өсуі бойынша анықталған бағыты жағына қарай бағытталған вектор
аргументінің өсуі бойынша анықталған бағыты жағына қарай бағытталған вектор
Егер мұндағы a(
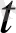 ) вектор функцияның орнына оның
) вектор функцияның орнына оның
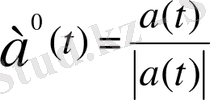 бірлік векторын алсақ, онда, оның годографы радиусі 1-ге тең сферада орналасқандықтан,
бірлік векторын алсақ, онда, оның годографы радиусі 1-ге тең сферада орналасқандықтан,
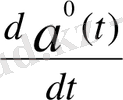 бірлік векторыдың туындысы
бірлік векторыдың туындысы
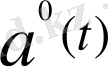 бірлік векторына перпендикуляр вектор болады (өйткені радиустың ұшынан өтетін жанама осы радиусқа перпендикуляр) . Ал
бірлік векторына перпендикуляр вектор болады (өйткені радиустың ұшынан өтетін жанама осы радиусқа перпендикуляр) . Ал
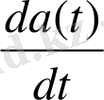 векторы үшін (егер
векторы үшін (егер
│а(
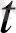 ) │тұрақты болмаса) бұл қасиет орындалмайды. Бірақ
) │тұрақты болмаса) бұл қасиет орындалмайды. Бірақ
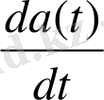 векторы а(
векторы а(
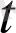 ) вектор-функциясына перпендикуляр │a(
) вектор-функциясына перпендикуляр │a(
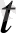 ) │
) │
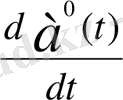 векторы мен осы а(
векторы мен осы а(
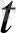 ) векторына коллинеар
) векторына коллинеар
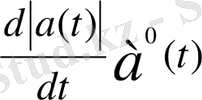 векторының қосындысына жіктеледі:
векторының қосындысына жіктеледі:
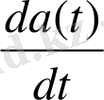 =
=
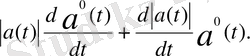 (1. 2. 1)
(1. 2. 1)
Бұл теңдіктің дұрыстығына көз жеткізу үшін, а(t) векторын
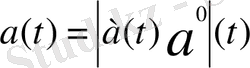 түрінде жазып алып, оны дифференциалдасақ болғаны.
түрінде жазып алып, оны дифференциалдасақ болғаны.
Материалдық нүктенің орын ауыстыру траекториясы (1. 2. 2-сурет) келесі теңдікпен а(t) = x(
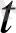 ) i+y(
) i+y(
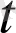 ) j+z(
) j+z(
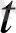 ) k немесе параметрлік теңдеулер бойынша берілсін:
) k немесе параметрлік теңдеулер бойынша берілсін:
х= x(
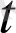 ), y=y(
), y=y(
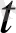 ), z=z(
), z=z(
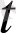 ),
),
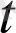 - уақыт.
- уақыт.
(1. 2. 2-сурет)
Онда Δа (
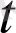 ) =
векторы нүктенің Δ
) =
векторы нүктенің Δ
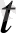 уақыт ішіндегі ауысқан орнын, ал
векторы нүкте қозғалысының Δ
уақыт ішіндегі ауысқан орнын, ал
векторы нүкте қозғалысының Δ
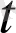 уақыт ішіндегі орташа жылдамдығын көрсетеді. Егер Δ
уақыт ішіндегі орташа жылдамдығын көрсетеді. Егер Δ
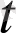 0 ұмтылдырып,
векторының шегіне өтсек, онда
шегі
0 ұмтылдырып,
векторының шегіне өтсек, онда
шегі
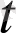 - уақыт кезеңіндегі v жылдамдық векторын береді. Сонымен, вектор - функцияның
- уақыт кезеңіндегі v жылдамдық векторын береді. Сонымен, вектор - функцияның
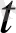 - нүктедегі туындысының механикалық мағынасы ол нүкте қозғалысының
- нүктедегі туындысының механикалық мағынасы ол нүкте қозғалысының
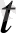 уақыт кезеңіндегі жылдамдық векторы екен: а'
= v(
уақыт кезеңіндегі жылдамдық векторы екен: а'
= v(
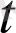 ) . Бұдан (10) теңдікті пайдалансақ:
) . Бұдан (10) теңдікті пайдалансақ:
V= + аалмыз.
Математикалық анализ курсынан х= x(
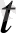 ), y=y(
), y=y(
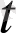 ), z=z(
), z=z(
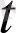 ) теңдеуімен берілген s доға ұзындығының туындысы да осы формуламен өрнектелетіні белгілі:
) теңдеуімен берілген s доға ұзындығының туындысы да осы формуламен өрнектелетіні белгілі:
+
Демек, вектор-функцияның нүктедегі туындысының модулі уақыт кезеңіндегі жылдамдық вектордың модулі) нүктесі сызатын s доғасы ұзындығының туындысына тең: V=
Ал вектор-функцияның
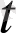 нүктедегі дифференциялының модулі ((13) теңдікті қараңыз) мен х= x(
нүктедегі дифференциялының модулі ((13) теңдікті қараңыз) мен х= x(
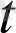 ), y=y(
), y=y(
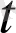 ), z=z(
), z=z(
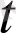 ) теңдеуімен берілген
s
доғаның дифференциалын: ds(
) теңдеуімен берілген
s
доғаның дифференциалын: ds(
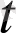 ) =
салыстырсақ,
теңдігін аламыз: вектор-функцияның
) =
салыстырсақ,
теңдігін аламыз: вектор-функцияның
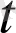 нүктедегі дифференциалының модулі
нүктедегі дифференциалының модулі
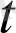 нүктесі сызатын
доғаның дифференциалына тең.
нүктесі сызатын
доғаның дифференциалына тең.
1. 3 СКАЛЯР ЖӘНЕ ВЕКТОР ӨРІСТЕРІ
Скаляр өріс
Қандай да бір физикалық құбылыс қарастырылатын кеңістіктің бөлігін немесе осы кеңістіктің өзін белгілеу үшін « өріс » ұғымы қолданылады.
Егер Ω жиынның әрбір Р нүктесіне
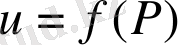 скалярлық шама сәйкес қосылса, онда Ω жиыннында
скаляр өрісі берілді
дейді.
скалярлық шама сәйкес қосылса, онда Ω жиыннында
скаляр өрісі берілді
дейді.
Егер кеңістікте қандай да бір OXYZ тікбұрышты координаттар жүйесі берілсе, онда скаляр өріске x, y, z - үш анымалдың (Р нүктенің координаттарының)
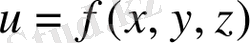 функциясы ретінде немесе Р нүктесініңрадиус-векторы r-дің
функциясы ретінде немесе Р нүктесініңрадиус-векторы r-дің
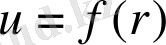 функциясы ретінде қарауға болады.
функциясы ретінде қарауға болады.
Анықтама.
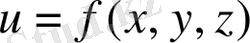 скаляр өрісінің деңгей беті деп,
скаляр өрісінің деңгей беті деп,
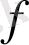 функциясы тек бір ғана мәнге ие болатын
функциясы тек бір ғана мәнге ие болатын
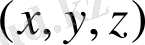 нүктелерінің геометриялық орнын, яғни
нүктелерінің геометриялық орнын, яғни
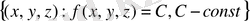 жиынын айтады.
жиынын айтады.
Екі өлшемді жағдайда
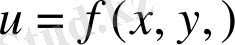 скаляр өрісінің деңгей сызығы деп жазықтықтағы
скаляр өрісінің деңгей сызығы деп жазықтықтағы
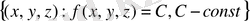 нүктелерінің жиынын айтады.
нүктелерінің жиынын айтады.
1-мысал.
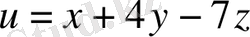 скаляр өрісінің деңгей бетін табу керек.
скаляр өрісінің деңгей бетін табу керек.
Анықтама бойынша,
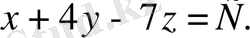 Бұл - параллель жазықтықтар жиынтығы.
Бұл - параллель жазықтықтар жиынтығы.
2-мысал.
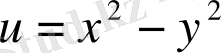 скаляр өрісінің деңгей сызығын табу керек.
скаляр өрісінің деңгей сызығын табу керек.
Берілген скаляр өрісінің деңгей сызығын анықтама бойынша табамыз:
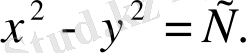 Мұнда, С=0 болса,
Мұнда, С=0 болса,
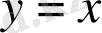 ,
,
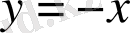 түзулер жұбын аламыз; С≠0 болса, гиперболалар жиынтығын аламыз.
түзулер жұбын аламыз; С≠0 болса, гиперболалар жиынтығын аламыз.
3-мысал.
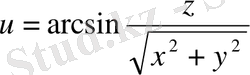 скаляр өрісінің деңгей бетін табу керек.
скаляр өрісінің деңгей бетін табу керек.
Мұнда келесі шарт орындалуы керек:
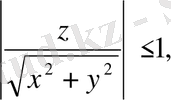 немесе
немесе
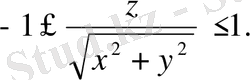 Бұл шарттан берілген скаляр өрісі
Бұл шарттан берілген скаляр өрісі
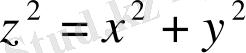 конусының сыртында және конустың О(0, 0, 0) төбесінен басқа нүктелерінде анықталатынын көреміз. Деңгей бетті табайық:
конусының сыртында және конустың О(0, 0, 0) төбесінен басқа нүктелерінде анықталатынын көреміз. Деңгей бетті табайық:
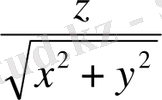 =C,
=C,
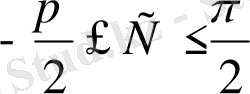 . Бұл -
. Бұл -
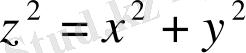 конусының сыртында орналасқан, симметрия өсі Oz және ортақ төбесі О(0, 0, 0) (бұл нүктеде скаляр өрісі анықталмаған) болатын дөңгелек конустар жиынтығы. Бұл жиынтықта
конусының сыртында орналасқан, симметрия өсі Oz және ортақ төбесі О(0, 0, 0) (бұл нүктеде скаляр өрісі анықталмаған) болатын дөңгелек конустар жиынтығы. Бұл жиынтықта
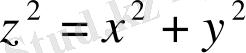 конусының өзі де жатады.
конусының өзі де жатады.
Бағыт бойынша туынды
Скаляр өріс u=ƒ(M) скаляр функциясы арқылы берілсін. Өрісте жатқан M 0 нүктесін алып, қандай да бір бағытты берілген s векторы бойынша таңдайық. Өрістен M 0 M векторы берілген s векторына коллинеар болатындай М нүктесін аламыз да, Δƒ арқылы Δƒ= ƒ(M) - ƒ(M 0 ) айырымын, Δ s арқылы M 0 M векторының ұзындығын: Δ s = │M 0 M│ белгілейміз.
Анықтама. Егер M 0 M s векторына параллель бола отырып, Δs 0 нөлге ұмтылғанда, қатынасының шегі бар болса, онда оны u=ƒ(M) функциясының s векторының бағыты бойынша алынған M 0 нүктедегі туындысы дейді және оны символымен белгілейді.
= M 0 M (1. 3. 1)
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz