Жоғары сыныптарда механикалық тербелістер мен толқындарды оқыту әдістемесі


Тақырыбы: механикалық тербелістер, механикалық толқындар
Мазмұны
Кіріспе . . .
1-тарау. Механикалық тербелістер тақырыбын оқыту әдістемесі . . .
Гармониялық тербелістер . . .
Еркін гармониялық тербелістердің жиілігі мен периодының системасының қасиеттеріне тәуелділігі . . .
Гармониялық тербелісті компьютермен модельдеп оқыту . . . Гармоникалық тербелістер кезіндегі энергияның айналуы . . .
Тербелістер фазасы . . .
Резонанстың қолданылуы және онымен күрес . . .
2-тарау. Механикалық толқындар тақырыбын оқыту әдістемесі . . .
Түрлі ортадағы дыбыстық толқындар . . .
Музыкалық дыбыстар мен шулар. Дыбыстың қаттылығы мен биіктігі . . .
Толқынның интерференциясы мен сынуы . . .
Дыбыстың таралуын оқытудағы әдістемелер . . .
Тест сұрақтары . . .
Механикалық толқындар және тербелістер тақырыбына арналған бақылау жұмысы . . .
Қорытынды . . .
Пайдаланылған әдебиеттер . . .
Кіріспе
Мұғалім пәнді оқытудың әдіс-тәсілдерін орынды пайдаланғанда ғана оқытудың мақсатына қол жеткізе алады. Сондықтан да оқытудың оқушы тұлғасын дамытуды қамтамасыз ететіндей неғұрлым тиімді әдіс - тәсілдерін таңдау мәселесі мұғалімнің алдында тұрған үлкен міндет болып саналады.
Сабақта уақытты ұтымды пайдаланудың ең бір дұрыс жолы - материалды блокпен оқыту. Бұл әдісті пайдалану, әсіресе тақырыптарды блоктарға бөліп жоспарлау мұғалімнен үлкен іскерлікті талап етеді.
Әртүрлі әдістемелік құралдарда ұсынылып жүрген дәстүрлі күнтізбелік жоспарларды пайдаланған кезде әр сабақ сайын дерлік жаңа тақырып өтіледі.
Демек, бір сабақта оқулықтың бір - екі параграфын түсіндіруге тура келеді. Бұл жағдайда оқушылар төрт -бес сабақтан кейін өтілген материалды ұмыта бастайды. Ал бір сабақты материалды бағдарлама деңгейінде игеру мүмкін емес, оның үстіне, көптеген мәселелер бүкіл тақырыпты тұтастай саналы
түрінде ой елегінен өткізіп зерделеуді талап етеді.
Күнтізбелік жоспарды мынандай ретпен қойған жөн.
1) тақырып ірі блоктарға бөлінеді, оған тақырыптағы ең басты мәселелер, негізгі ұғымдар мен заңдар енгізіледі;
2) жаңа материалды пысықтау сабақтары мен семинар-сабақтар, онда есептер шығарып, сапалық және эксперименттік тапсырмалар талданады, қысқа мерзімді өзіндік жұмыстар және оқушылардың біліміндегі олқылықтарды түзету жұмыстары жүргізіледі;
3) зертханалық жұмыстарды орындау сабақтары;
4) консультация - сабақтар немесе жалпылап қорыту сабақтары;
5) сынақ-сабақтары немесе бақылау жұмыстарын жүргізу сабақтары жоспарланады.
Орта мектептерде жоғары сынып оқулығының «Тербелістер мен толқындар» тарауын оқытуға бағдарлама бойынша 5сағат бөлінген. Тақырыпқа талдау жасай отырып, негізгі ұғымдарды анықтап алуға болады, олар: механикалық және электромагниттік тербелістер, тербелмелі қозғалысты сипаттайтын негізгі шамалар; математикалық және серіппелі маятниктер, тербелмелі контур. Оқулық материалының берілу логикасынан тербеліс кезіндегі энергияның түрленуі, еркін және еріксіз тербелістер тақырыптары түсіп қалғандай болып көрінеді, шын мәнінде электромагниттік тербелістер ұғымын еркін және ерксіз тербелістер, резонанс ұғымдарын өтпей тұрып-ақ түсіндіруге болады. Сондықтан «блокқа» мына материалдар біріктіріледі: механикалық және электромагниттік тербелістер, математикалық және серіппелі маятниктер, тербелмелі контур.
Сонда осы «Тербелістер» тарауы бойынша тақырыптық жоспар шамамен мына түрде болады.
1) механикалық және электромагниттік тербелістер, тербелмелі қозғалысты сипаттайтын негізгі шамалар. Математикалық және серіппелі маятниктер, тербелмелі контур (бұл жаңа материалды түсіндіру сабағы дәріс түрінде өткізіледі)
2) Семинар-сабақ
3) Материалды пысықтау сабағы. Өзіндік жұмыс.
4) Ν3 лабораториялық жұмыс: Маятниктің көмегімен еркін түсу үдеуін анықтау.
5) Тербелістер тарауы бойынша сынақ сабағы.
Бірінші сабақта §2-3 және §4 бір-ақ беріледі. Бір қарағанда мұндай ауқымды материалды 45 минут ішінде түсіндіру мүмкін емес сияқты көрінеді, бірақта тәжірибе көрсеткендей, сабаққа мұқият дайындала отырып, бұл материалды 30-35 минутта түсіндіруге болады. Сабақтың соңғы 10 минуты қорытындылауға бөлінеді. Осылай жаңа тақырып түсіндірілген әр бір сабақтың соңында өтілген материал қорытындыланып отырады.
Материалды қысқаша қорытынды ретінде тағы да бір рет қайталау керек, яғни механикалық тербелістер деген не, оның негізгі сипаттамалары қандай тербеліс жиілігі неге тең, период пен жиілік арасында қандай байланыс бар, жиіліктің өлшем бірлігі не дегенге тоқталады. Осылайша өткенді қысқаша қорытындылау. материалдағы ең маңыздыны ажырату оқушыға үйде сабақ дайындаған кезде белгілі бір жоспар қызметін атқарады. Үйге тапсырма бергенде оқушыларға тақырыпты жаттап алу міндет емес екенін, олардан оқу материалындағы ең маңызды нәрсені ажырату, яғни тербелмелі қозғалыстың мәнін ұғу, тербелмелі қозғалыстың басқа қозғалыс түрлерінен айырмашылығын түсіну талап етілетініне назар аударылады. Бірінші сабақта тербелмелі контур толық қарастырылмайды.
Тақырып бойынша келесі сабақ-семинар. Семинар сабақтарда өткенді тереңірек қайталау, материалды тереңдете түсіндіру ұйымдастырылды. Оқушыларды есептер шығара білуге, құралдармен жұмыс жасауға, материалды талдай білуге және т. б. дағдыландыру керек. Оқушылар жауап беруді, материалды түсінікті етіп жеткізуді, пікір таластыруды үйренеді. Нақты айтқанда, тақырып бойынша осы екінші сабақ білімді тереңдету сабағы болып табылады. Сабақтың негізгі бөлігінде оқушылар оқулықпен жұмыс жасайды. Сұрақтар күрделену ретімен алдын ала тақтаға жазылып қойылады. Әр оқушы өзі нашар меңгерген немесе жауабының дұрыстығына күмәнданатын сұрақтарға дайындалады. Оқушылардың өз бетімен жұмыс істеуіне 10 минут уақыт беріледі. Әрі қарай әңгіме-сұхбат барысында сұрақтардың жауаптары нақтыланып, материал оқулық бойынша талданады. Ал тақырыпты меңгермеген оқушылар енді мұғалімнің көмегімен оқулықпен қайта жұмыс жасайды.
Тақырып бойынша үшінші сабақ тағы да семинар-сабақ болады, онда оқушылардың жеке қабілетіне қарай түрлі деңгейдегі есептер талданады. Семинар-сабақтарда талданған есептердің санына әуестенбеген жөн. Мұнда тақырып бойынша көбінесе типтік есептерді таңдаған дұрыс. Дайындығы жоғары оқушыларға сабақта да, үйге де неғұрлым күрделірек есептер беру керек. Әрі қарай материал басқа блоктардағы семинар-сабақтарда жүйелі түрде қайталанып отырады.
Жоспар бойынша келесі сабақ тақырыптағы түсіндіруге уақыт неғұрлым аз бөлінген оқу материалын неғұрлым талдамалап, сығыңқы берілген мәселелерді мұқият қарастыруға арналады.
Әрбір сабақтың соңында ненің жақсы меңгеріліп, ненің әлі де болса пысықтай түсуді қажет ететіндігін, үйде қандай жұмыстар жүргізу керек екендігін айтып, қорытындылап отыру керек.
Оқушылардың білімін тексеру олардың іс-әрекетін бақылап, оған түзетулер енгізу арқылы жүзеге асырылады. Оқушылардан тек сынақ қана алынып қоймай, тақырыпты зерделеу барысында лабораториялық жұмыстар орындалып, өзіндік жұмыстар жүргізіледі.
1 тарау. Механикалық тербелістер тақырыбын оқыту әдістемесі
1. Еркін және еріксіз тербелістер . Тербелмелі қозғалыстар, өте кең тараған. Бір затты тербелтіп жіберу қиын емес.
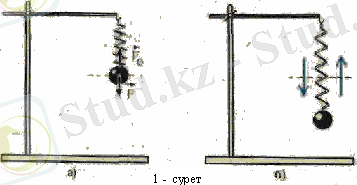 Пружинаны алып штативке ілейік. Пружинаның төменгі бос ұшына металл шарик бекітейік. Пружина созылады да, серпімділік күші
Пружинаны алып штативке ілейік. Пружинаның төменгі бос ұшына металл шарик бекітейік. Пружина созылады да, серпімділік күші
 шарикке әсер ететін
шарикке әсер ететін
 ауырлық күшін теңгереді (1, а-сурет) . Егер енді шарикті ақырын төмен тартып апарып, қоя беріп, оны тепе-теңдік қалпынан шығарса, сонда ол жоғары-төмен ырғаптап, едәуір қызық қозғалыс жасайды (1, б-сурет) . Дене біресе бір жаққа, біресе екінші жаққа қарай алма-кезек орын ауыстыратын осы сияқты қозғалысты тербелмелі деп атайды. Уақыт өтуіне қарай тербелістер өшеді де, ақырында шарик тоқтайды.
ауырлық күшін теңгереді (1, а-сурет) . Егер енді шарикті ақырын төмен тартып апарып, қоя беріп, оны тепе-теңдік қалпынан шығарса, сонда ол жоғары-төмен ырғаптап, едәуір қызық қозғалыс жасайды (1, б-сурет) . Дене біресе бір жаққа, біресе екінші жаққа қарай алма-кезек орын ауыстыратын осы сияқты қозғалысты тербелмелі деп атайды. Уақыт өтуіне қарай тербелістер өшеді де, ақырында шарик тоқтайды.
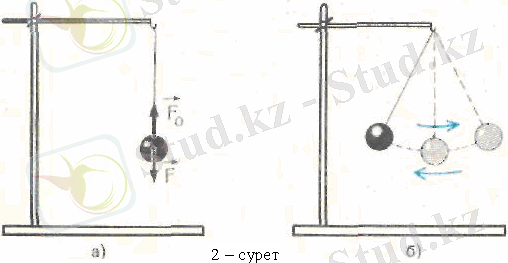 Шарикті жіпке асып қойып, оны әлгіден гөрі де оңай тербелтуге болады. Тепе-теңдік қалыпта жіп вертикаль тұрады да, шарикке әсер ететін
Шарикті жіпке асып қойып, оны әлгіден гөрі де оңай тербелтуге болады. Тепе-теңдік қалыпта жіп вертикаль тұрады да, шарикке әсер ететін
 ауырлық күші жіптің
ауырлық күші жіптің
 серпімділік күшімен теңгеріледі (2, а-сурет) . Егер шарикті бұрып апарып, қоя берсе, ол оңға-солға теңселіп (2, б-сурет), тербеліс өшкенде барып тоқтайды. Жіпке асулы шарик - ең қарапайым маятник. Жіпке асулы шарик, оған тек ауырлық күші әсер еткен жағдайда ғана, маятник бола алатынын ескеру керек. Бұл күшті туғызатын жер шары тербелмелі системаға кіреді, қысқаша біз оны (жүйені) жай маятник деп атаймыз. Негізінде маятник деп - ауырлық күштің әсерімен тербеліс жасай алатын, жіпке асылған не оське бекітілген денені айтады. Бірақ мұнда ось
серпімділік күшімен теңгеріледі (2, а-сурет) . Егер шарикті бұрып апарып, қоя берсе, ол оңға-солға теңселіп (2, б-сурет), тербеліс өшкенде барып тоқтайды. Жіпке асулы шарик - ең қарапайым маятник. Жіпке асулы шарик, оған тек ауырлық күші әсер еткен жағдайда ғана, маятник бола алатынын ескеру керек. Бұл күшті туғызатын жер шары тербелмелі системаға кіреді, қысқаша біз оны (жүйені) жай маятник деп атаймыз. Негізінде маятник деп - ауырлық күштің әсерімен тербеліс жасай алатын, жіпке асылған не оське бекітілген денені айтады. Бірақ мұнда ось
дененің ауырлық центрі арқылы өтпеуі керек. Маятник деп шегеге ілінген сызғышты, люстраны, рычагты, таразының күйентесті тәрізділерді айтуға болады.
Сонда тербелмелі қозғалыстың өзіне тән белгісі не? Бәріненде көзге түсетіні, тербеліс кезінде дененің қозғалыстары қайталанып отырады және қайталап отырады дерліктей болғандығы. Мысалы, маятник сол жақтағы ең шеткі қалпынан оң жақтағы шеткі қалпына барып және керісінше жүріп, яғни толық бір тербеліс жасап, қайтадан сондай қозғалыс жасайды. Егер қозғалыс дәлме-дәл қайталанып отырса, онда оны периодты деп атайды.
Тербелістер дегеніміз - белгілі бір уақыт арасында интервал өткен сайын дәлме-дәл не жуықтап қайталайтын қозғалыстар.
Автомобиль двигателіндегі поршеньдердің, толқын бетіндегі қалтқының, жел соққанда ағаш бұтағының, біздің жүргеніміздің соғу қозғалыстары периодты қайталанады. Осының бәрі тербелістердің әр түрлі мысалдары.
Еркін тербелістер . Қозғалысын біз зерттеп отырған денелер тобын механикада - денелер жүйесі (немесе жүйе) деп атайды. Жүйенің денелерінің арасында әсер ететін күштерді ішкі күштер деп атайды. Жүйеге кірмейтін денелер тарапынан жүйенің денелеріне әсер ететін күштері сыртқы күштер деп аталады.
Тербелістің ең қарапайым түрі - жүйені тепе-теңдік қалпынан шығарғаннан кейін, система ішінде ішкі күштердің әсерінен пайда болатын тербелістер. Ондай тербелістерде - еркін тербелістер деп атайды. Пружинадағы жүйенің немесе жіпке асулы жүктің тербелістері - осы еркін тербелістердің мысалдары. Осы системаларды тепе-теңдік қалпынан шығарғаннан кейін периодты өзгеретін сыртқы күштердің әсерінсіз, денелер тербеліп тұратын жағдайлар туады.
Еріксіз тербелістер . Егер қолымызбен үстел үстіндегі кітапты ілгерілі-кейінді қозғасақ, ол тербелістер жасайды, бірақ бұл тербелістер еркін емес. Осы берілген жағдайда кітаптың тербелістерін туғызған, шамасы мен бағыты дүркін-дүркін өзгеріп отыратын, қол тарапынан тиген әсер.
Периодты өзгеретін сыртқы күштердің әсерінен денелердің жасайтын тербелістері еріксіз деп аталады.
Атап айтқанда іштен жанатын двигательдің цилиндрлеріндегі поршеньдердің тербелістері, іс машинасының тербелістері де еріксіз.
2. Еркін тербелістердің туу жағдайлары .
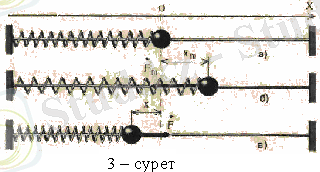
Жүйе ішіндегі еркін тербелістер туу үшін, оның қасиеттері қандай болуы керек екенін ашайық. Әуелі, пружинаның серпімділік күшінің әсерінен, горизонталь жолмен шариктің шыбық бойымен тербелістерін қарастырғанымыз ыңғайлы болар. Вертикаль пружинаға асулы шариктің тербелісін анализдеу бұдан гөрі күрделірек, өйткені бұл жағдайда пружинаның айнымалы серпімділк күші мен тұрақты ауырлық күші екеуі бір мезгілде қабаттаса әсер етеді. Сөйтсе де, бұл жағдайлардың қайсысында болса да тербелістер сипаты мейлінше бірдей.
Егер шарикті тепе-теңдік қалпынан (3, а-сурет) оңға қарай ығыстырсақ, онда пружинаның ұзындығы Х
М
-ге ұзарады да (3, б-сурет), шарикке пружина тарапынан
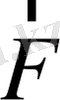 серпімділік күші әсер ете бастайды. Бұл күш Гук заңы бойынша пружинаның деформациясына пропорционал да, солға қарай бағытталады. Осы
серпімділік күші әсер ете бастайды. Бұл күш Гук заңы бойынша пружинаның деформациясына пропорционал да, солға қарай бағытталады. Осы
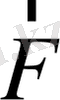 күштің әсерімен шарик солға қарай үдей қозғалады да, жылдамдығын үлкейтеді. Бұл кезде
күштің әсерімен шарик солға қарай үдей қозғалады да, жылдамдығын үлкейтеді. Бұл кезде
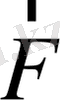 күш кеми бастайды, өйткені пружинаның деформациясы кішірейеді. Шарик тепе-теңдік қалпына жеткенде, пружинаның серпімділік күші нольге тең. Ендеше, Ньютонның екінщі заңы бойынша, шариктің үдеуі де нольге теңеледі.
күш кеми бастайды, өйткені пружинаның деформациясы кішірейеді. Шарик тепе-теңдік қалпына жеткенде, пружинаның серпімділік күші нольге тең. Ендеше, Ньютонның екінщі заңы бойынша, шариктің үдеуі де нольге теңеледі.
Осы кезге дейін шарик жылдамдығы максималь теңдік қалыпта тоқтап қалмай, ол инерция салдарынан солға қарай қозғала береді. Пружина бұл кезде қысқарады, оның нәтижесінде, енді оңға қарай бағытталған серпімділік күші пайда болады, шариктің қозғалысын тежейді (3, в-сурет) . Бұл күш оңға бағытталған үдеу де, шариктің
х
ауытқу модуліне тура пропорционал болып, модулі бойынша өсе береді. Ал жылдамдық кеми береді де, сол жақ шеттегі қалыпта нольге айналады. Бұдан кейін шарик оңға қарай үдей қозғала бастайды. Ауытқу модулі
х
кемуімен бірге
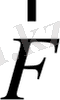 күш модулі бойынша кемиді де, тепе-теңдік қалыпта тағы нольге айналады. Бірақ бұл мезетте шарик жылдамдық алып үлгереді де, сондықтан оңға қарай қозғала береді. Бұл қозғалыстан пружина созылады да, солға бағытталған күш пайда болады. Ол жақтағы шеткі қалыпта әбден тоқтағанға шейін шариктің қозғалысы тежеле береді де, осыдан соң барлық процесс басынан қайталана береді.
күш модулі бойынша кемиді де, тепе-теңдік қалыпта тағы нольге айналады. Бірақ бұл мезетте шарик жылдамдық алып үлгереді де, сондықтан оңға қарай қозғала береді. Бұл қозғалыстан пружина созылады да, солға бағытталған күш пайда болады. Ол жақтағы шеткі қалыпта әбден тоқтағанға шейін шариктің қозғалысы тежеле береді де, осыдан соң барлық процесс басынан қайталана береді.
Егер үйкеліс болмағанда, шариктің қозғалысы ешқашан тоқтамас еді. Бұл үйеліс (атап айтқанда, ауа кедергісі) бар, онан соң кедергі күштің бағыты, шариктің оңға қарай қозғалысында да ылғи жылдамдықтың бағытына қарама-қарсы. Сондықтан үйкеліс шариктің қозғалысын тежейді де, оның тербеліс құлашы біртіндеп қозғалыс тоқтағанға шейін кеміп
 отырады. Үйкеліс аз кезінде шарик көп тербеліс жасағаннан кейін ғана өшу байқалады. Егер онша ұзақ емес уақыт мерзім ішінде шарик қозғалысын қатыстыратын болсақ, оның тербелістерінің өшуін елемей-ақ тастауға болады. Мұндай жағдайда кедергі күшінің қозғалысқа тигізетін әсерін ескермеуге болады. Шариктің гоизонталь жөнімен тербелістері кезіндегі үйкелісті азайту үшін кескінделген қондырғыны пайдаланады.
отырады. Үйкеліс аз кезінде шарик көп тербеліс жасағаннан кейін ғана өшу байқалады. Егер онша ұзақ емес уақыт мерзім ішінде шарик қозғалысын қатыстыратын болсақ, оның тербелістерінің өшуін елемей-ақ тастауға болады. Мұндай жағдайда кедергі күшінің қозғалысқа тигізетін әсерін ескермеуге болады. Шариктің гоизонталь жөнімен тербелістері кезіндегі үйкелісті азайту үшін кескінделген қондырғыны пайдаланады.
Егер кедергі күші үлкен болса, аз ғана уақыт мерзімі ішіндегі оның әсерін елемей тастауға болмайды. Пружинаға ілген шарикті стақандағы тұтқыр сұйыққа, мысалы глицеринге батырыңыз (4-сурет) . Егер пружина едәуір жұмсақ болса, онда тепе-теңдік қалпынан шықса шарик атымен тербелмейді. Ол серпімділік күшінің әсерінен тепе-теңдік қалпына қайта келе салады (4-сурет. Пунктирленген сызықтар), кедергі күшінің әсері есебінен тепе-теңдік қалыпта оның жылдамдығы нольге тең деп айтарлық.
Жүйе ішіндегі еркін тербелістер өшу үшін ең басты 2 шарт екенін енді ұғынуға болады. Осы 2 шарт орындалуы қажет.
Біріншіден: денені тепе-тең қалпынан шығарған кезде, жүйе ішінде, тепе-теңдік қалыпқа қайтаруға тырысатын, күш өнуі керек. Біз қарастырған жүйедегі пружина дәл солай әсер етеді: шарикті солға жылжытқанда да, оңға жылжытқанда да, серпімділік күш тепе-теңдік қалыпқа бағытталған.
Екіншіден, жүйедегі үйкеліс мейлінше аз болуы қажет, өйтпесе тербелістер тез өшеді не мүлде пайда болмайды. Өшпейтін тербелістер тек үйкелісі жоқ кезде мүмкін бола алады.
Шарттың екеуі де, еркін тербелістер пайда болады, кез-келген жүйенің қайсысында болса да ортақ дұрыс, жарамды. Осыны басқа бір қарапайым жүйеде - маятникте сынайық.
3. Математикалық маятник
 Қарапайым маятниктер - ұзын жіпке асулы ауыр шарикті қарастырайық. Егер шариктің өлшемдері жіптің ұзындығынан көп кіші болса, онда әлгі өлшемдерді елемей-ақ шарикті материялық нүкте деп қарастыруға болады. Жіптің созылуын да елемейміз, өйткені ол да мейлінше аз. Шариктің массасымен салыстырғанда жіптің массасы елерлік емес. Сонымен, реал маятниктің- жіпке асулы (жіп әрине қозғалғанда аздап деформацияланады және оның массасы бар) шариктің орнына біз оңай модель: созылмайтын жіпке асулы материялық нүктені қарастыра аламыз. Маятниктің осындай үлгісін - математикалық маятник деп атайды. Ұзын жіңішке жіпке ілулі кішкене шарик іс-жүзінде математикалық маятниктің орнына жүре алады. Маятникті тепе-теңдік қалпынан шығарайық та қойып жіберейік. Шарикке күш әсер етеді: ауырлық күші
Қарапайым маятниктер - ұзын жіпке асулы ауыр шарикті қарастырайық. Егер шариктің өлшемдері жіптің ұзындығынан көп кіші болса, онда әлгі өлшемдерді елемей-ақ шарикті материялық нүкте деп қарастыруға болады. Жіптің созылуын да елемейміз, өйткені ол да мейлінше аз. Шариктің массасымен салыстырғанда жіптің массасы елерлік емес. Сонымен, реал маятниктің- жіпке асулы (жіп әрине қозғалғанда аздап деформацияланады және оның массасы бар) шариктің орнына біз оңай модель: созылмайтын жіпке асулы материялық нүктені қарастыра аламыз. Маятниктің осындай үлгісін - математикалық маятник деп атайды. Ұзын жіңішке жіпке ілулі кішкене шарик іс-жүзінде математикалық маятниктің орнына жүре алады. Маятникті тепе-теңдік қалпынан шығарайық та қойып жіберейік. Шарикке күш әсер етеді: ауырлық күші
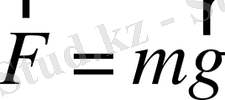 бұл вертикаль төмен бағытталған және жіптің
бұл вертикаль төмен бағытталған және жіптің
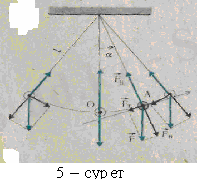
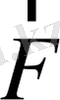 серпімділік күш - бұл жіптің бойымен бағытталған (5-сурет) . Маятник қозғалғанда оған әрине кедергі күші әсер етеді. Бірақ біз оны ескермеуге болатындай аз деп есептейміз.
серпімділік күш - бұл жіптің бойымен бағытталған (5-сурет) . Маятник қозғалғанда оған әрине кедергі күші әсер етеді. Бірақ біз оны ескермеуге болатындай аз деп есептейміз.
Маятник қозғалысының динамикасын айқын түсіну үшін, ауырлық күшін құраушыға жіктеген ыңғайлы: жіптің бойымен бағытталған
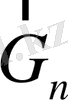 нормаль құраушы және
нормаль құраушы және
 тангенциал құраушы, бұл шарик траекториясына жанаманың бойымен жіпке перпендикуляр бағытталған. Жіптің
тангенциал құраушы, бұл шарик траекториясына жанаманың бойымен жіпке перпендикуляр бағытталған. Жіптің
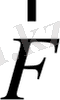 серпімділік күші және ауырлық күшінің құраушысы, маятниктің жылдамдығына перпендикуляр болады да, оған нормаль немесе центрге тартқыш үдеу береді: бұл шеңбер доғасының - маятник траекториясының центріне бағытталған. Осы күштердің жұмысы нольге тең. Сондықтан кинетикалық энергия жөніндегі теорема бойынша, олар маятниктің жылдамдығын модулі бойынша өзгертпейді. Бұлардың әсерінің салдарының жылдамдық векторы тек үнемі бағытын өзгертіп отырады да, кез-келген уақыт мезгілінде жылдамдық шеңбер доғасына жанама бойынша бағытталады.
серпімділік күші және ауырлық күшінің құраушысы, маятниктің жылдамдығына перпендикуляр болады да, оған нормаль немесе центрге тартқыш үдеу береді: бұл шеңбер доғасының - маятник траекториясының центріне бағытталған. Осы күштердің жұмысы нольге тең. Сондықтан кинетикалық энергия жөніндегі теорема бойынша, олар маятниктің жылдамдығын модулі бойынша өзгертпейді. Бұлардың әсерінің салдарының жылдамдық векторы тек үнемі бағытын өзгертіп отырады да, кез-келген уақыт мезгілінде жылдамдық шеңбер доғасына жанама бойынша бағытталады.
Ауырлық күшінің
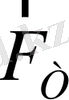 тангенциал құраушысы тангенциал үдеу дегенді туғызады, бұл жылдамдықтың модулі өзгерісін сипаттайды. Маятниктің толық үдеуі тангенциал және нормаль үдеулерінің геометриялық қосындысына тең.
тангенциал құраушысы тангенциал үдеу дегенді туғызады, бұл жылдамдықтың модулі өзгерісін сипаттайды. Маятниктің толық үдеуі тангенциал және нормаль үдеулерінің геометриялық қосындысына тең.
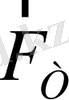 құраушысының әсерімен маятник шеңбер доғасы бойымен төмен қарай жылжығандығын арттыра қозғалады. Маятник қозғалған сайын ауырлық күшінің тангенциал құраушысы (ол тепе-теңдік қалыпқа бағытталған) де, маятник тепе-теңдік қалыптан өте берген кезде, нольге тең болады. Өзінің инерттілігінің салдарынан маятник әрі қарай қозғалып жоғары көтеріле береді. Мұнда енді
құраушысының әсерімен маятник шеңбер доғасы бойымен төмен қарай жылжығандығын арттыра қозғалады. Маятник қозғалған сайын ауырлық күшінің тангенциал құраушысы (ол тепе-теңдік қалыпқа бағытталған) де, маятник тепе-теңдік қалыптан өте берген кезде, нольге тең болады. Өзінің инерттілігінің салдарынан маятник әрі қарай қозғалып жоғары көтеріле береді. Мұнда енді
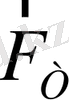 құраушы жылдамдыққа қарсы бағытталады. Сондықтан маятниктің жылдамдығы кеми береді және жіп пен вертикаль арасындағы бұрыш үлкейген сайын, ол шапшаңырақ кемиді. Өйткені бұрыш үлкейгенде ауырлық күшінің осы құраушысы өседі. Ең жоғары нүктеде маятник тоқтаған мезетте оның тангенциал үдеуі максимал (ең үлкен шамада) және тепе-теңдік қалыпқа қарай бағытталған. Бұдан соң маятниктің жылдамдығы артып, енді ол қайтадан тепе-теңдік қалыпқа қарай қозғалады. Тепе-теңдік өткен соң ол бастапқы қалпына қайтады (егер кедергі күші аз болып, азғана уақыт интервалының ішіндегі оның жұмысы елеусіз болса) . Маятникті тұтқыр сұйығы бар сауытқа батырып, тербелістер мүлдем не өте тез өшетінін аңғарамыз.
құраушы жылдамдыққа қарсы бағытталады. Сондықтан маятниктің жылдамдығы кеми береді және жіп пен вертикаль арасындағы бұрыш үлкейген сайын, ол шапшаңырақ кемиді. Өйткені бұрыш үлкейгенде ауырлық күшінің осы құраушысы өседі. Ең жоғары нүктеде маятник тоқтаған мезетте оның тангенциал үдеуі максимал (ең үлкен шамада) және тепе-теңдік қалыпқа қарай бағытталған. Бұдан соң маятниктің жылдамдығы артып, енді ол қайтадан тепе-теңдік қалыпқа қарай қозғалады. Тепе-теңдік өткен соң ол бастапқы қалпына қайтады (егер кедергі күші аз болып, азғана уақыт интервалының ішіндегі оның жұмысы елеусіз болса) . Маятникті тұтқыр сұйығы бар сауытқа батырып, тербелістер мүлдем не өте тез өшетінін аңғарамыз.
4. Тербелістік қозғалыс динамикасы. Серпімділік күшінің әсерінен тербелетін дененің қозғалысының теңдеуі.
Дененің тербеліс процесін (пружинаның серпімділік күшінің әсерімен болатын немесе жіпке асулы шариктің тербелістерін) сан жағынан сипаттау үшін Ньютон механикасының заңдарын пайдалану керек.
Ньютонның 1-ші заңы бойынша
 дене массасының
дене массасының
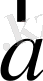 үдеуге көбейтіндісі денеге түсірілген барлық күштердің
үдеуге көбейтіндісі денеге түсірілген барлық күштердің
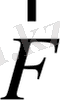 тең әсерлісіне тең
тең әсерлісіне тең
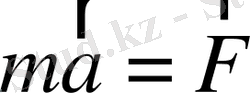 (1. 1)
(1. 1)
Пружинаның әсерінен (3-суретке қараңыз) горизонталь бойымен түзу сызықты қозғалатын шарик үшін қозғалыс жасайық. ОХ осьті оңға бағыттайық. Координаталардың санақ басы тепе-теңдік қалыпқа сәйкес келеді дейік (3, а-сурет) . Сондықтан
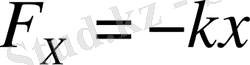 (1. 2)
(1. 2)
мұндағы
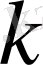 - пружина қатаңдығы.
- пружина қатаңдығы.
Шарик қозғалысының теңдеуі былай жазылады
 (1. 3)
(1. 3)
мұндағы
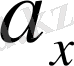 - ОХ ось бағытындағы үдеу проекциясы. Теңдеудің (1. 3) сол және оң бөліктерін
- ОХ ось бағытындағы үдеу проекциясы. Теңдеудің (1. 3) сол және оң бөліктерін
 -ге бөліп табамыз
-ге бөліп табамыз
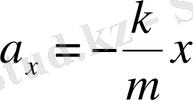 (1. 4)
(1. 4)
 масса мен
масса мен
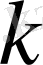 қатаңдық тұрақты шамалар болғандықтан, олардың
қатаңдық тұрақты шамалар болғандықтан, олардың
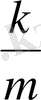 қатынасы да тұрақты шама. Біз серпімділік күштің әсерімен болатын дене тербелістерінің теңдеуін шығарып алдық. Ол өте оңай: дене үдеуінің
қатынасы да тұрақты шама. Біз серпімділік күштің әсерімен болатын дене тербелістерінің теңдеуін шығарып алдық. Ол өте оңай: дене үдеуінің
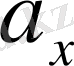 проекциясы оның х координатасына (қарама-қарсы таңбамен алынған) тура пропорционал.
проекциясы оның х координатасына (қарама-қарсы таңбамен алынған) тура пропорционал.
Математикалық маятниктің қозғалыс теңдеуі.
Созылмайтын жіптегі шариктің тербелісі кезінде ол ұдайы шеңбер (оның радиусы жіптің
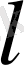 ұзындығына тең) доғасының бойымен қозғалады. Сондықтан кез-келген мезетте шариктің орны бір ғана шамамен - жіптің вертикальда α оң таңбалы, солға бұрылса теріс таңбалы деп есептейік (5-сурет) . Маятник жылдамдығының модулі ауырлық күшінің тангенциал
ұзындығына тең) доғасының бойымен қозғалады. Сондықтан кез-келген мезетте шариктің орны бір ғана шамамен - жіптің вертикальда α оң таңбалы, солға бұрылса теріс таңбалы деп есептейік (5-сурет) . Маятник жылдамдығының модулі ауырлық күшінің тангенциал
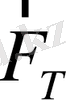 құраушысының әсерінен үздіксіз өзгереді. Маятник жылдамдығын модулінің өзгеру шапшаңдығы тангенциал үдеумен анықталады. Ауырлық күшінің шарик траекториясына жанамаға түсірілген проекциясы маятниктің жібі тепе-теңдік қалыптан α бұрышқа бұрылған мезетте, былай өрнектеледі:
құраушысының әсерінен үздіксіз өзгереді. Маятник жылдамдығын модулінің өзгеру шапшаңдығы тангенциал үдеумен анықталады. Ауырлық күшінің шарик траекториясына жанамаға түсірілген проекциясы маятниктің жібі тепе-теңдік қалыптан α бұрышқа бұрылған мезетте, былай өрнектеледі:
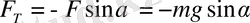 Equation. 3 (1. 5)
Equation. 3 (1. 5)
Мұнда «
__
» таңба
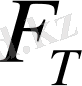 Equation. 3 мен α-ның таңбалары қарама-қарсы дегенді білдіреді. Ньютонның 2-ші заңы бойынша:
Equation. 3 мен α-ның таңбалары қарама-қарсы дегенді білдіреді. Ньютонның 2-ші заңы бойынша:
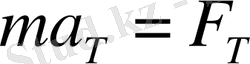 Equation. 3 немесе
Equation. 3 немесе
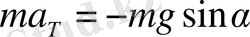 Equation. 3 (1. 6)
Equation. 3 (1. 6)
мұндағы
 Equation. 3 - траекторияға жанамадағы үдеу проекциясы. Осы теңдеудің 2 бөлігінде
Equation. 3 - траекторияға жанамадағы үдеу проекциясы. Осы теңдеудің 2 бөлігінде
 Equation. 3 -ге бөліп, табамыз:
Equation. 3 -ге бөліп, табамыз:
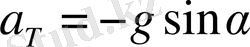 Equation. 3 (1. 7)
Equation. 3 (1. 7)
Осыған дейін маятник жібі вертикальдан кез келген бұрышқа ауытқуы мүмкін деп жорығанбыз. Бұдан былай оларды кішкене бұрыштар деп есептейді. Кішкене бұрыштар жағдайында, бұрышты радианмен өлшесе:
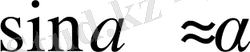
Олай болса, былайша алса болады
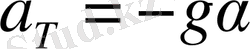 (1. 8)
(1. 8)
ОА доғасының ұзындығын
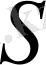 өрнектесе, былай жазса болады:
өрнектесе, былай жазса болады:
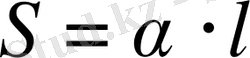
нәтижеде:
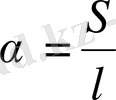 (1. 9)
(1. 9)
Осы өрнекті α орнына қойса, онда:
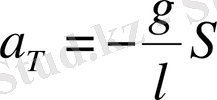 (1. 10)
(1. 10)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz