Функционалдық анализдің негізгі анықтамалары мен теоремалары

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 39 бет
Таңдаулыға:

Мазмұны

Кіріспе

I. Функционалдық анализдің негізгі анықтамалары мен теоремалары .

1. 1 Сызықты және нормаланған кеңістіктер

1. 2 Метрикалық кеңістіктер

1. 3 Евклид және Гильберт кеңістіктер

1. 4 Кері операторлар

1. 5 Түйіндес операторлар

II. Жартылай периодты Дирихле есебі үшін өз-өзіне түйіндес емес оператордың бір класының шешімінің бар болуы

2. 1 Эллипстік теңдеулер

2. 1. 1 Лаплас теңдеуі

2. 1. 2 Пуассон теңдеуі

2. 2 Шеңбер үшін бірінші қисық есеп

2. 2 Жартылай периодты Дирихле есебі үшін өз-өзіне түйіндес емес оператордың бір класының шешімінің бар болуы

Қорытынды

Әдебиеттер

1. 1. Сызықты және нормаланған кеңістіктер

Сызықты кеңістіктер

Анықтама. Егер қайсыбір 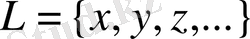жиынында:

1. Кез келген 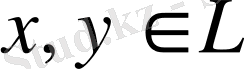элементтері үшін олардың қосындысы деп аталатын 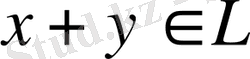элементі анықталған болса және бұл екі элементті қосу амалы үшін мына қаситтер орындалса:

1. 1. 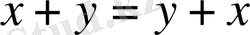(қосудың коммутативтік қасиеті) ;

1. 2. 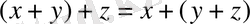(қосудың ассоциативтік қасиеті) ;

1. 3. Кез келген үшін теңдігі орындалатын бір ғана элементі бар болуы (нөлдік элемент) ;

1. 4. Кез келген үшін 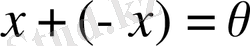теңдігі орындалатын 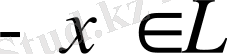элементі (х-ке қарама-қарсы элемент) бар және ол әр х үшін біреу ғана болса және

2. Кез келген және кез келген нақты саны үшін 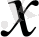элементі мен 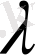санының көбейтіндісі деп аталатын 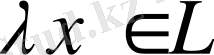элементі анықталған болса және бұл элементті санға көбейту амалы мен элеметтерді қосу амалдары мына төмендегі шарттарды қанағаттандыратын болса.

2. 1.

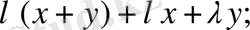
2. 2.

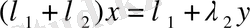
2. 3.

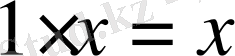
2. 4.

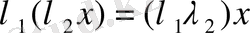
онда бұл жиыны сызықтық кеңістік деп аталады.

жиынының элементтерін қосу және оларды санға көбейту амалдары үшін қойылған осы шарттар сызықтық кеңістіктің аксиомалары деп аталады.

жиынының элементтері көбейтілетін сандар жиыны ретінде нақты сандар жиыны , немесе комлекс сандар жиыны алынуына қарай нақты сызықтық кеңістік, немесе комплекс сызықтық кеңістік пайда болады.

Егер жиынының өзі де нақты немесе комплекс сандардан тұратын болса, онда санды санға қосу және көбейту амалдары үшін бұл аксиомалар орындалатыны жақсы белгілі. Сондай-ақ, жазықтықтағы немесе кеңістіктегі векторларды қосу және оларды санға көбейту амалдары үшін де бұл шарттар орындалатыны белгілі. Демек, әдеткі амалдар анықталған сандар жиыны, немесе векторлар жиыны сызықтық кеңістіктің мысалдары болып табылады.

Сонымен, қайсібір жиында кез-келген екі элементтің қосындысы және элементтің нақты санға көбейтіндісі анықталса және бұл амалдар жоғаоыдағы аксиомаларды қанағаттандырса, онда бұл жиын сызықтық кеңістікке айналады. Мысалы:

1. 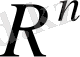арқылы n- өлшемді координаттық кеңістік белгіленеді.

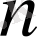Бұл кеңістікте жиыны ретінде -өлшемді 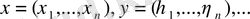векторлары қарастырылады. Мұнда сондай-ақ -кез келген нақты сандар - вектордың координаттары. Екі вектордың қосындысы 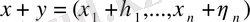түрінде, яғни берілген векторлардың аттас координаталарын қосу нәтижесінде пайда болған вектор ретінде анықталады, ал 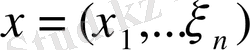векторының санына көбейтіндісі 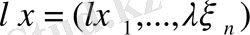түрінде, яғни осы вектордың әрбір координатын санына көбейтуден пайда болған вектор ретінде анықталады. Бұл анықтама бойынша осы 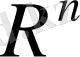жиынының элементтері үшін анықталған қосу және санға көбейту амалдары вектордың координаттарына, яғни сандарға қолданылады. Сондықтан жоғарыда келтірілген 1. 1. -1. 2. аксиомаларының орындалуы нақты сандардың қасиеттерінен тікелей шығады. Онан әрі, 1. 3. аксиомасындағы нөлдік элемент ретінде 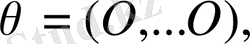ал, 1. 4. аксиомасына сәйкес, 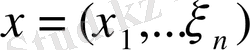элементіне қарама - қарсы элемент ретінде 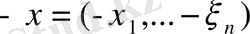элементі болады.

Ал, 2. 1. -2. 4. қасиеттері орындалатындығы нақты сандар қасиеттерінен тікелей шығады. Осылай анықталған сызықтық кеңістік 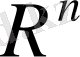арқылы таңбаланады.

2. 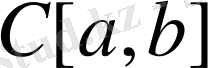түрінде 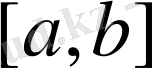- кесіндісінде үзіліссіз функциялардың жиыны белгіленеді. Мұнда функцияларды қосу және санға көбейту амалдары әдеттегідей анықталған. Үзіліссіз екі функцияның қосындысы да, үзіліссіз функцияның санға көбейтіндісі де үзіліссіз функция болғандықтан 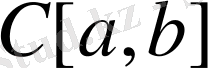жиынында бұл амалдар анықталған. Қай функцияның да мәні сан болғандықтан, 1-мысалдағыдай, бұл мысалда да аксиомалардың орындалу олардалуы олардың нақты сандар үшін орындалатындығынан өзінен өзі шығады. Нөлдік элемент ретінде бұл кеңістікте үшін 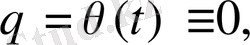яғни 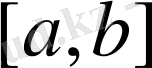кесіндісіне нөлге тепе-тең функция алынады.

Нормаланған сызықтық кеңістіктер

Аналитикалық геометрияда координатты кеңістіктегі әрбір 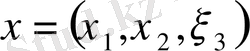векторының ұзындығы

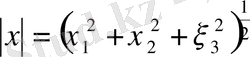
теңдігімен анықталған сан екені белгілі. Енді осы ұғымды жалпылап, кез-келген сызықтық кеңістіктің элементтері үшін норма ұғымын анықтаймыз. Бұл анықтаманың негізінде ұзындыққа тән қасиеттер жатқанын аңғаруға болады.

Сонымен, кез келген сызықтық кеңістік берілген болсын.

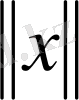Анықтама. Егер әрбір үшін нақты сан мәнді функциясы анықталса және ол мына мына шарттарды қанағаттандыратын болса:

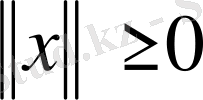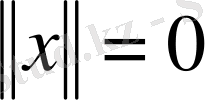1) және тек болғанда ғана (нормаланған теріс еместік шарты) ;

2) кез келген 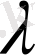саны үшін 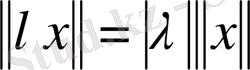(норманың біртектілік шарты) ;

3) кез келге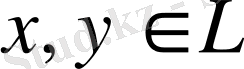н үшін 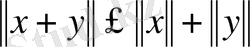(үшбұрыш теңсіздігі) онда кеңістігінде норма анықталған дейміз.

Анықтамада келтірілген 1), 2), 3) шарттары норманың аксиомалары деп аталады.

Норма анықталған сызықтық кеңістік нормаланған сызықтық кеңістік деп аталады.

Сызықтық кеңістігінің 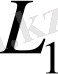ішжиынындағы элементтердің нормасы анықталғандығы түсінікті. Сондықтан 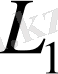жиынының жеке өзі нормаланған сызықтық кеңістік болып табылады. Осы кеңістік нормаланған сызықтық кеңістігінің ішкеңістігі деп аталады.

Нормаланған сызықтық кеңістіктің мысалдары.

1. 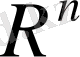-сызықтық кеңістікте норма анықтап, оны нормаланған сызықтық кеңістікке айналдырамыз. Мұнда жатқан әрбір элемент (вектор) 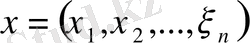үшін норманы

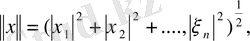(1)

теңдігімен анықтаймыз. Осылай анықталған норма норманың аксиомаларын қанағаттандыратынын тексеру қажет. Бірінші шарттың орындалатыны (1) теңдігінің оң жағындағы өрнек көрер көзге теріс емес екендігінен айқын. Онан әрі, егер 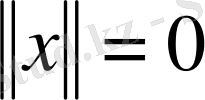болса, онда барлық 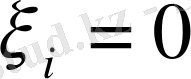болғаны. Себебі, егер қайсыбір 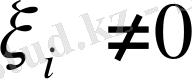болса, онда (1) теңдігінің оң жағындағы өрнектің мәні оң сан болатыны айқын. Сонымен, егер 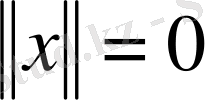болса, онда x векторының барлық координаттары нөлге тең: 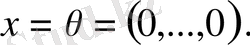Керісінше, егер 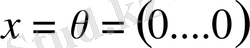болса, онда 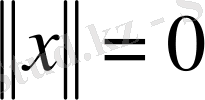екені айқын.

Екінші аксиома да оңай тексеріледі:

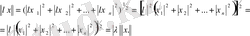(2)

Үшінші аксиома, яғни үшбұрыш теңсіздігі орындалатынын дәлелдеу үшін алдымен Коши теңсіздігін еске алайық. Кез-келген 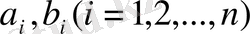нақты сандар үшін

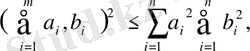(3)

теңсіздігі орындалады. Бұл теңсіздіктің екі жағынан квадрат түбір алып, оны мына түрде де жазуға болады:

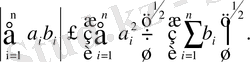(4)

Енді осы теңсіздікті пайдаланып (1) нормасы үшін үшбұрыш теңсіздігін дәлелдейік (жазуды жеңілдету үшін 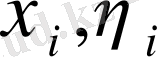нақты сандар деп есептеп, модуль таңбасын жазбаймыз) :

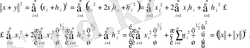
Теңсіздіктің екі жағынан квадрат түбір алып, үшбұрыш теңсіздігіне келеміз.

Сонымен (1) теңдігімен анықталған норма шынында да норма аксиомаларын қанағаттандыратыны айқын болды. 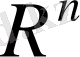жиыны нормаланған сызықтық кеңістікке айналды. Бұл кеңістік, әдетте, арифметикалық Евклид кеңістігі деп, ал норма (1) -Евклид нормасы (немесе, Евклидтік норма) деп аталады.

2. 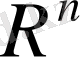сызықтық кеңістігінде норманы басқаша, атап айтқанда,

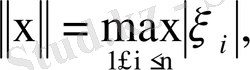(5)

теңдігі арқылы енгізіп, сол жиында анықталған тағы бір нормаланған сызықтық кеңістікке келеміз. Норманың аксиомалары орындалатынын тексеру бұл жолы тіпті оңай. Шынында да, (5) өрнегінен норманың теріс сан болмайтыны айқын және 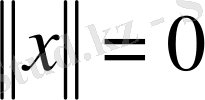болуы барлық 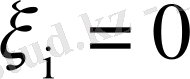болғанда, тек қана осы жағдайда болады, яғни (нөл-вектор болғаны) .

Сондай-ақ, екінші, үшінші аксиомалардың тексерілуі де қиын емес:

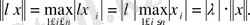(6)

Егер 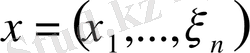және 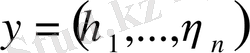кеңістіктің кез-келген екі векторы болса, онда

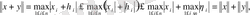
яғни үшбұрыш теңсіздігі орындалады екен.

Осы анықталған нормаланған сызықтық кеңістікті 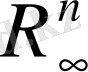түрінде таңбалайтын боламыз.

1. 2. Метрикалық кеңістіктер

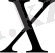-кез келген жиын болсын. Оның элементтерін 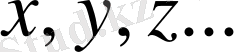әріптерімен белгілейміз.

Екі айнымалылы, нақты сан мәнді 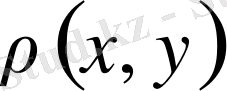функциясы осы 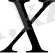жиынының элементтерінде анықталып және мына төмендегі шарттарды қанағаттандыратын болсын:

1. 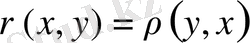(симметриялық шарты) .

2. және =0 теңдігі тек қана болғанда орындалады (тепе-теңдік шарты) .

3. Кез келген 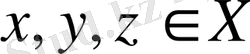элементтері үшін

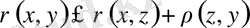, (1)

теңсіздігі орындалады. (Бұл теңсіздік үшбұрыш теңсіздігі деп аталады) .

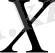-жиынында анықталған, осы қасиеттерге ие 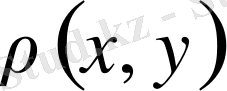функциясы арақашықтық немесе метрика деп аталады. Метрика үшін қойылған үш шарт метрика аксиомалары деп аталады.

Анықтама. Метрика анықталған 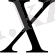жиынын “метрикалық кеңістік” деп атайды.

Метрикалық кеңістік 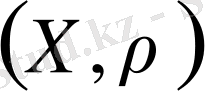түрінде белгіленеді, бірақ көбінесе қысқаша, тек жиынның ғана таңбасын көрсетіп, 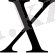арқылы белгілейміз.

Үшбұрыш теңсіздігінің салдары ретінде шығатын мына теңсіздіктерді атап өтейік. Метрикалық кеңістікте жатқан кез келген 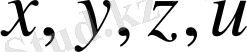нүктелері үшін үшбұрыш теңсіздігін қайталай қолданып, мына теңсіздіктерді жазайық:

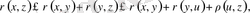
яғни,

(*)

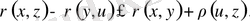Осыған ұқсас,

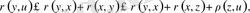
яғни,

(**)

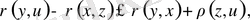Енді (*), (**) теңсіздіктері

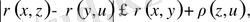
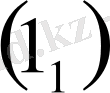
теңсіздігіне пара-пар екені айқын. Бұл әдетте, Төртбұрыш теңсіздігі деп аталады. Осы теңсіздіктен 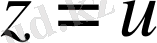болған жағдайда

теңсіздігі шығады, ал бұл- екінші үшбұрыш теңсіздігі.

Тұжырым. - кез келген нормаланған сызықтық кеңістік болсын.

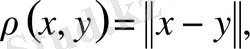(2)

теңдігі осы кеңістікте метриканы анықтайды.

Дәлелдеуі. Шарт бойынша -нормаланған сызықтық кеңістік. Метриканың бірінші аксиомасы орындалатыны (2) теңдігінен айқын. Сондай-ақ, 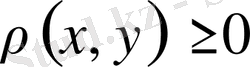екендігі де норманың сәйкес қасиетінен шығады. Егер 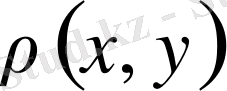=0 болса, онда , демек норманың қасиеті бойынша, 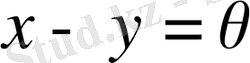, яғни x=y.

Енді метриканың үшінші аксиомасын, яғни (1) теңсіздігін дәлелдейік. Кеңістіктің кез келген 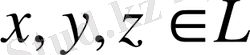элементтерін алып, норманың үшінші аксиомасын пайдаланып, метрика үшін үшінші аксиоманың орындалатынын көреміз:

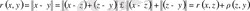(3)

(2) теңдігінің норманы анықтайтыны, сонымен бірге жиыны метрикалы жиын, яғни метрикалық кеңістік болғаны дәлелденді.

Осы тұжырымнан шығатын маңызды бір қорытынды-жоғарыда келтірілген нормаланған сызықтық кеңістіктің мысалдарында әр кеңістіктің нормасын (2) теңдігіне қойып, метрика анықтаса, ол кеңістік метрикалық кеңістікке айналады.

Сызықтық кеңістіктегі операторлар

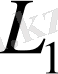және -кез келген сызықтық кеңістіктер болсын.

Анықтама. Егер әрбір элементіне белгілі бір элементі сәйкес қойылған болса, онда кеңістігінде оператор анықталған дейміз.

Осы операторды 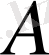символымен таңбаласақ, онда 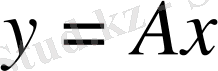теңдігі 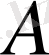операторының элементін 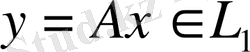элементіне бейнелейтінін көрсетеді. Сонымен, 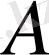операторы кеңістігін 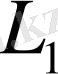кеңістігінің қайсыбір ішжиынына (мүмкін түгел 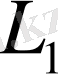кеңістігіне) аударатын бейнелеу. Бұл жағдай басқаша 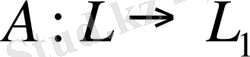түрінде де жазылады.

Бұл анықтамадан, функционал-оператордың дербес жағдайы, атап айтканда, функционал дегеніміз 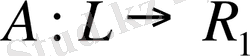(комплекс кеңістік жағдайында ) операторы екені көрінеді. Жалпы жағдайда, егер әрбір 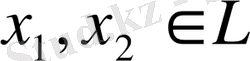элементтері және кез-келген 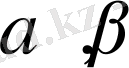сандары үшін

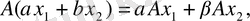(7)

теңдігі орындалатын болса, онда 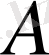сызықтық оператор деп аталады.

Сызықтық операторлардың мысалдары

Нөл-оператор. -сызықтық кеңістік. яғни бұл бұл оператор кеңістіктегі кез-келген элементті нөлдік элементке аударады. Сызықтылық шарты (7) теңдігі орындалатынын тексеру оңай.
Бірлік оператор. - кез-келген сызықтық кеңістік, =болсын.

теңдігімен анықталған 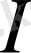операторы бірлік оператор деп аталады. Бұл

оператор кеңістіктің әр элементін осы элементтің өзіне бейнелейді.

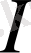
сызықтық оператор екені оның анықтамасынан айқын.

Матрица. болсын. матрица жәнеэлементіматрицасы менвекторының көбейтіндісі болсын. Сонда бұл матрицасызықтық операторын анықтайды. Бұл оператордың сызықтық қасиеті матрицаларды көбейту ережесінің салдары болады.

Шынында да, егер болса, онда матрицаларды көбейту ережесі бойынша

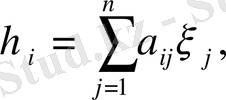(9)

Егер және кез-келген екі вектор болса, ал олардың матрицасымен түрленген бейнелері

және

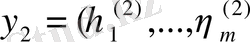
Векторлары болса, онда (9) теңдігі бойынша векторының нші координаты тең:

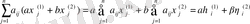
ал, екінші жағынан, бұл векторының нші координаты, демек, (7) теңдігі орындалады.

4. Функцияға көбейту операторы. 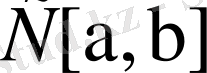кеңістігінен жеке алынған тиянақты

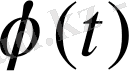функциясы және кез-келге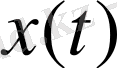н үшін 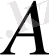операторы

(10)

теңдігімен анықталған болсын. Бұл функциясына көбейту операторы деп аталады. Бұл сызықтық оператор екені айқын.

5. Интегралдық оператор. 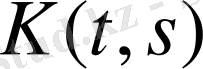функциясы

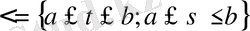
квадратында үздіксіз болсын. Кез-келген 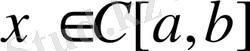функциясы үшін

операторды

(11)

теңдігімен анықтайық. Онда яғни (11) теңдігімен операторы анықталды. Интегралдың сызықтық қасиетінен бұл оператордың да сызықтық оператор екендігі тікелей шығады.

Операторларға қолданылатын амалдар.

Сызықтық кеңістікте анықталған операторларға қосу, көбейту және операторды санға көбейту амалдарын қолданып, жаңа сызықтық оператор анықтауға болады. Осы айтылған амалдарды анықтайық.

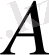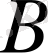1. Операторларды қосу. Егер сызықтық кеңістігінде және сызықтық операторлары анықталған болса, онда олардың қосындысы

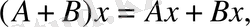(12)

теңдігімен анықталады, яғни қосынды оператор әрбір 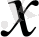элементін осы элементтің бейнелерінің қосындысына аударады.

2. Операторды санға көбейту. 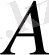операторының 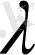санына көбейтіндісі, яғни операторы

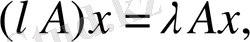(13)

теңдігімен анықталады. операторы кеңістігінде анықталған болса, онда да осы кеңістікте анықталғандығы айқын.

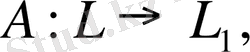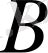3. Операторлардың бірін екіншісіне көбейту. ал операторы 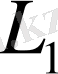кеңістігінде анықталған болсын. Онда сондықтан 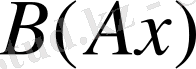элементі анықталған. Енді 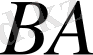операторы

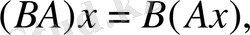(14)

теңдігімен анықталады. Бұл анықтама қисынды болуы үшін 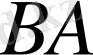көбейтіндісінде бірінші тұрған оператордың мәндері екінші оператордың анықталу жиынында жатуы шарт.

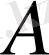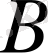Егер және сызықтық операторлар болса, онда (12) -(14) теңдіктерімен анықталған операторлар да сызықтық операторлар екенін тексеру қиын емес. Мысалы, 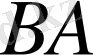операторының сызықтық қасиетін тексерейік:

4. Оператордың дәрежелері. Егер 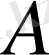операторы кеңістігінде анықталған және оның мәндері 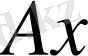осы кеңістікте жататын болса, онда 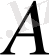операторының дәрежелері 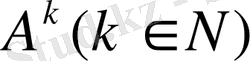келесі түрде анықталады:

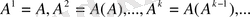5. Кері оператор. 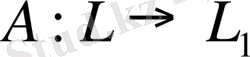сызықтық операторы берілсін. Оның мәндерінің жиынын 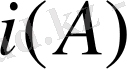символымен белгілейік және оны 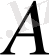операторының бейнесі деп атайық. Басқаша айтқанда, 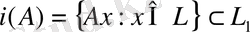жиыны. Егер 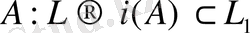сәйкестігі биекция болса, яғни әрбір 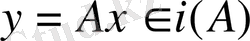элементіне тек элементі сәйкес қойылған болса, онда бірмәнді 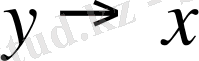бейнелеуі анықталады. Осы оператор 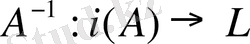түрінде таңбаланады және ол 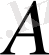операторына кері оператор деп аталады.

Осы анықтама бойынша 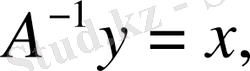демек, 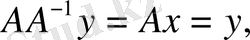яғни 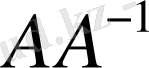операторы 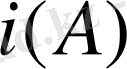жиынында анықталған бірлік оператор. Сондай-ақ, 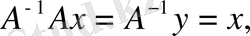демек, 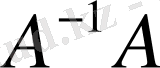операторы кеңістігінің бірлік операторы.

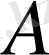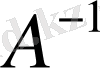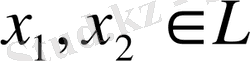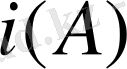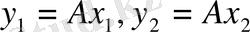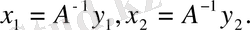
Егер сызықтық оператор болса, онда оған кері операторы да сызықтық оператор болатынын дәлелдейік. Егер кез-келген екі элемент және олардың жиынында жатқан бейнелері болсын. Онда сызықтық оператор, демек,

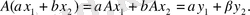
Осыдан, кері оператордың анықтамасы бойынша

Сызықтық оператордың нормасы

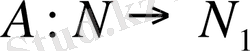сызықтық операторын қарастырайық.

Анықтама. Егер барлық үшін

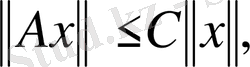(1)

теңсіздігі орындалатын С саны бар болса, онда 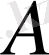шенелген оператор деп аталады.

Мұнда теңсіздіктің сол жағындағы норма 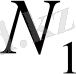кеңістігіндегі, ал оң жағындағы норма кеңістігіндегі элементтің нормасы. Шенелген оператор кеңістігіндегі шенелген жиынды 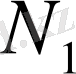кеңістігіндегі шенелген жиынға аударатыны (1) теңсіздігінен көрінеді.

(1) теңсіздігі орындалатындай 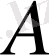сандарының инфинумы 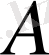операторының нормасы деп аталады және түрінде белгіленеді. Оператордың нормасын

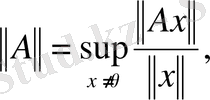(2)

теңдігімен анықтауға да болады. Супремумның мәні ақырлы екені (1) теңсіздігінің салдары.

Бұл анықтамалар өзара пара-пар екеніне көз жеткізейік. Екінші анықтамадан супремумның анықтамасы бойынша 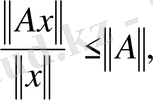теңсіздігі, ал осыдан теңсіздігі шығатыны айқын. Соңғы теңсіздікті (1) теңсіздігімен салыстырып, 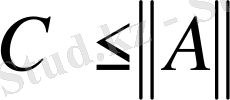теңсіздігіне сай саны табылатынын көреміз. Егер 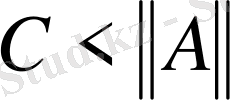деп жорысақ, онда (1) теңсіздігі бойынша 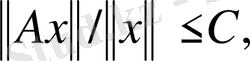ал мұның екі жағынан супремум алып 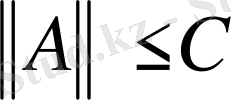теңсіздігіне келер едік. Демек, (1) теңсіздігіндегі саны (2) өрнегімен анықталған санынан кіші бола алмайды, яғни .

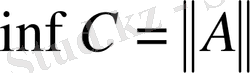Норманы анықтайтын (2) теңдігінде 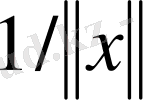санын бөлшектің алымындағы норманың ішіне енгізіп, 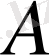сызықтық оператор екенін ескеріп, 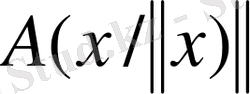түрінде жазайық. Сонда, 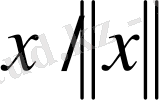векторының нормасы 1-ге тең. осыған орай, норманың анықтамасын үшінші түрде жаза аламыз:

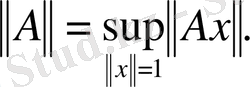(3)

Сызықтық оператордың нормасы норма аксиомаларын қанағаттандырады. Егер 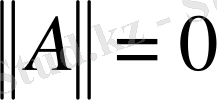болса, онда 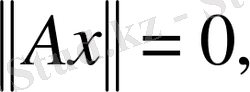демек, яғни 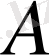-нөл-оператор. Норманың біртектілік қасиеті оның анықтамасынан айқын. Енді үшбұрыш теңсіздігін тексеру үшін (3) теңдігін пайдаланайық. Жоғарыдағы теңсіздігін және операторлардың қосындысының анықтамасын ескере отырып,

теңсіздігін, сонан соң бұл теңсіздіктің екі жағынан 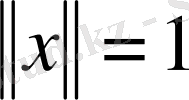шартын қанағаттандыратын элементтер векторлары бойынша супремум алып,

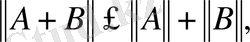(4)

теңсіздігіне келеміз. Ұқсас жолмен

(5)

теңсіздігі дәлелденеді.

Оператордың үздіксіздігі.

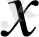Егер кеңістігінде элементтердің тізбегі элементіне жинақталатын болса және олардың бейнелері 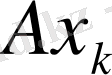тізбегі 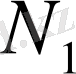кеңістігінде 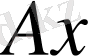элементіне жинақталса, онда 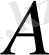операторын 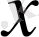элементінде үздіксіз деп айтамыз. Басқаша айтқанда, егер 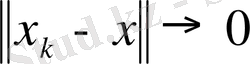кезінде 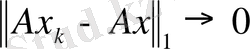болуы 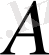операторының 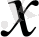нүктесінде үздіксіздігін анықтайды. Мұнда нормасы кеңістігінде, ал 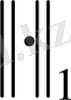нормасы 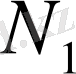кеңістігінде анықталған.

Шенелген сызықтық оператор туралы келесі тұжырымды дәлелдейік.

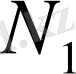Теорема. кеңістігін кеңістігіне бейнелейтін сызықтық оператор 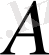үздіксіз болуы үшін оның шенелген болуы қажетті және жеткілікті шарт.

Қажеттілігі. 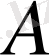шенелмеген деп жориық. Онда (1) теңсіздігі орындалатындай С саны табылмайды, яғни натурал 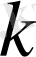санын қалай алсақ та,

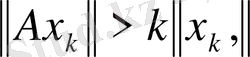(6)

теңсіздігі орындалатын элементі табылады. Осы элементі бойынша 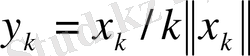тізбегін құрсақ, онда яғни . Бірақ, (6) теңсіздігінің салдарынан, 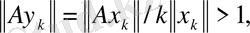яғни 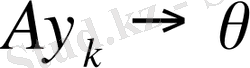болуы мүмкін емес, яғни нүктесінде операторы үздіксіз болмады. Бұл теорема шартына қайшы, демек шенелмеген оператор деген жору теріс болды.

Жеткіліктілігі. 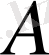операторы шенелген болсын (яғни (1) теңсіздігі кеңістіктің барлық нүктелерінде орындалады) және яғни 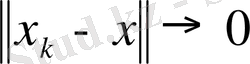болсын. Онда,

яғни 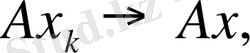демек, 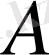үздіксіз оператор. Теорема дәлелденді.

1. 3. Евклид және Гильберт кеңістіктері

Евклид кеңістігі

Екі вектордың скаляр көбейтіндісі аналитикалық геометрия курсында анықта лып, кейін бұл ұғым 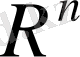кеңістігінде жалпыланған түрде, дәл айтқанда, кез келген 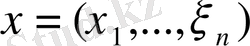және векторлар үшін олардың скаляр көбейтіндісі 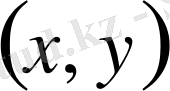түрінде таңбаланып, және

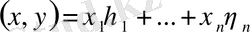(1)

теңдігімен анықталғаны мәлім. Енді скаляр көбейтінді ұғымы жалпы сызықтық кеңістіктерге анықталады.

Анықтама. Егер - сызықтық кеңістігінде кез келген 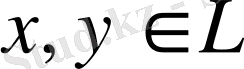үшін екі айнымалы, сан мәнді функция 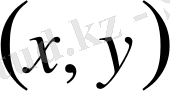анықталған және ол төмендегі шарттарды қанағаттандыратын болса:

1. 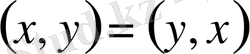(симметриялық қасиеті)

2. 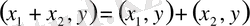(аддитивтік қасиеті)

3. 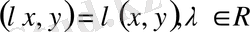(комплекс кеңістік жағдайында ) (біртектілік қасиеті)

4. 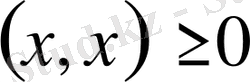және 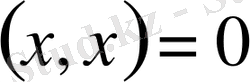тек қана болғанда ғана мүмкін, онда кеңістігінде скаляр көбейтінді анықталған дейміз. 1-4 шарттары скаляр көбейтіндінің аксиомалары деп аталады.

Скаляр көбейтінді анықталған сызықтық кеңістік, әдетте, Евклид кеңістігі деп аталады. Евклид кеңістігін Е әріпімен белгілейік.

Евклид кеңістігінің мысалдары.

1. 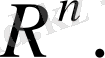Бұл кеңістікте скаляр көбейтінді (1) теңдігімен анықталғаны белгілі. 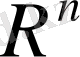кеңістігінде анықталған Евклид нормасы мен 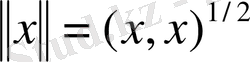теңдігімен анықталған норма бірдей екені айқын: 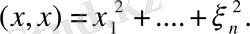Мұндай жағдайда норманың екі анықтамасы өзара үйлесімді дейміз. 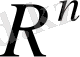кеңістігінің Евклид метрикасы бойынша толық екендігі жоғарыда дәлелденді. Сонымен, 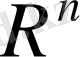-ақырлы өлшемді, толық Евклид кеңістігі.

2. 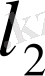. Бұл кеңістікте кез-келген екі элемент және үшін скаляр көбейтіндіні

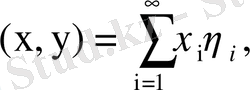(2)

теңдігімен анықтайық. Қатарлар үшін Коши теңсіздігінен бұл (2) қатарының кез-келген 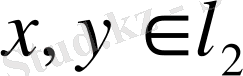элементтері үшін жинақты екенін қорытамыз. Скаляр көбейтіндінің аксиомалары орындалатыны да айқын. Осы скаляр көбейтінді арқылы 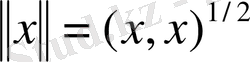теңдігімен анықталған табиғи норма

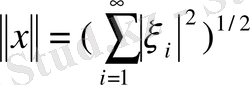, (3)

теңдігімен анықталған нормамен үйлесімді. Ал бұл норма арқылы анықталған метрика бойынша 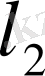толық кеңістік. Демек, 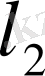өлшемі ақырсыз, толық Евклид кеңістігінің мысалы болып табылады.

Енді толық емес Евклид кеңістігінің бір мысалын келтірейік.

3. 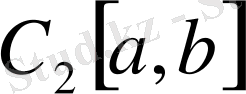. 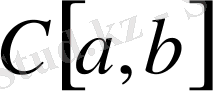сызықтық кеңістігінің кез-келген элементтері 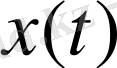және 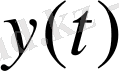үзіліссіз функцияларының скаляр көбейтіндісін

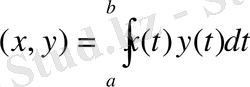, (4)

теңдігімен анықтайық. Бұл анықтама скаляр көбейтіндінің аксиомаларына сай екенін тексеру қиын емес. Скаляр көбейтінді (4) теңдігімен енгізілген 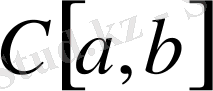жиыны Евклид кеңістігіне айналады. Осы кеңістікті 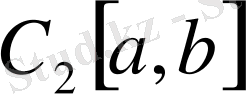түрінде белгілейік. Мұндағы табиғи норма

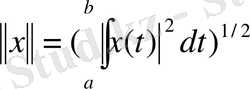, (5)

екендігі (4) теңдігінен айқын. Бұл норма бойынша 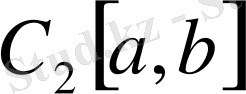кеңістігінде анықталатын метрика

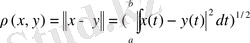. (6)

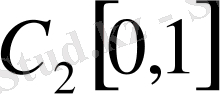кеңістігінде 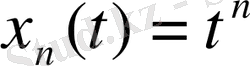функцияларының тізбегін қарастырайық. Егер тізбек нөмірлері және болса, онда

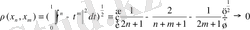Демек, 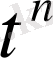функциялары 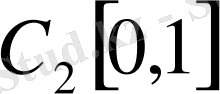кеңістігінде фундаменталь тізбек болғаны. Ал 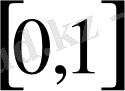кесіндісінде 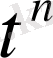тізбегі әр нүктеде жинақты, бірақ оның шегі үзілісті функция, яғни 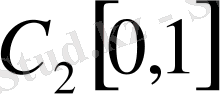кеңістігіне жатпайды. Демек, 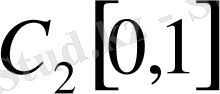толық кеңістік емес.

Гильберд кеңістігі

Анықтама. Өлшемі ақырсыз, толық Евклид кеңістігі Гильберд кеңістігі деп аталады.

Бұл кеңістікті әріпімен белгілейміз және тек сепарабель кеңістіктерді қарастырамыз. Сонымен, келесіде арқылы белгіленген кеңістік мына шарттарға сай екеніне зейін салайық:

1) -скаляр көбейтінді анықталған сызықтық кеңістік, яғни Евклид кеңістігі;

2) -скаляр көбейтінді арқылы анықталған нормаға сәйкес метрикасы бойынша толық кеңістік;

3) -өлшемі ақырсыз кеңістік;

4) -сепарабель кеңістік.

Жоғарыда келтірілген Евклид кеңістіктерінің мысалдарынан тек 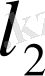кеңістігі ғана осы шарттардың бәріне де сай, демек 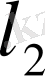-Гильберт кеңістігі екенін көреміз.

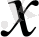кеңістігінде тізбегі элементіне жинақталады дегеніміз, кезде

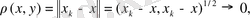
яғни айырымының скаляр квадраты нөлге ұмтылады деген сөз.

Скаляр көбейтінді өзінің екі аргументі бойында үздіксіз функция екенін дәлелдейік.

Шынында да, егер 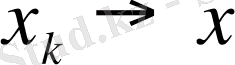және болса, онда скаляр көбейтіндінің аддитивтік қасиетін және Шварц теңсіздігін пайдаланып,

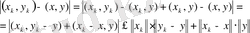
теңсіздігіне келеміз. Ал мұнда шенелген тізбек, себебі 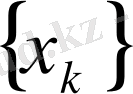шегі бар тізбек. Шарт бойынша кезд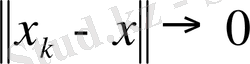е және 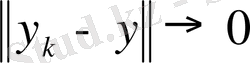, демек,

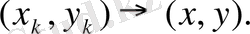
Гильберт кеңістіктерінің изоморфизмі.

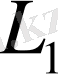Анықтама. Егер және сызықтық кеңістіктерінің элементтерінің арасында сызықтық амалдарды сақтайтын биекция болса, онда бұл кеңістіктер арасында изоморфизм бар дейміз.

Айқынырақ айтқанда, егер 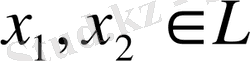және 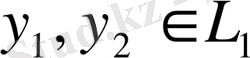элементтері арасындағы биекция бойынша 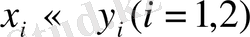сәйкестіктері болса, онда олардың ұқсас сызықтық комбинациялары да сәйкес болу керек:

Анықтама. Толық ортонормал векторлардың жүйесі бар кеңістігін өлшемі саналымды Гильберт кеңістігі деп атаймыз.

Тұжырым. Өлшемі саналымды кеңістігі сепарабель кеңістік болады.

Шынында да, мұндағы толық жүйенің элементтерінің сызықтық комбинациялары тығыз жиын, демек, кез-келген векторының 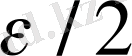маңайында 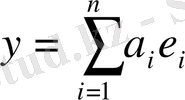сызықтық комбинациясы табылады, яғни 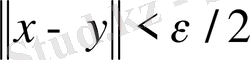. Енді әрбір 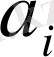санын рационал 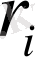санына ауыстырып, сәйкес комбинация құрып, векторын табайық. Сонда 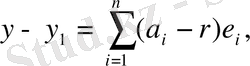сондықтан егер 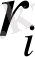сандарын 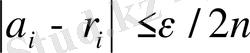теңсіздігіне сай етіп алсақ, онда 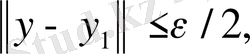демек,

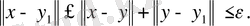
Сонымен, кез-келген 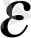-маңайында рационал коэффициенттермен алынған комбинациясы бар болды, яғни осындай комбинациялар жиыны да кеңістігінде тығыз орналасқан. Ал бұл жиынның саналымды екені түсінікті.