Ауырлық центрі. Параллель күштер центрі

Пән: Физика
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 8 бет
Таңдаулыға:

Мәнжазба

Тақырыбы:Ауырлық центрі. Параллель күштер центрі. Жазық денелердің және қималардың ауырлық центрінің координаттары

2015

Жоспар:

1. Ауырлық центрі 2. Параллель күштер центрі 3. Қатты дененің ауырлық центрі. Дененің ауырлық центрінің координаттары. Ауырлық центрінің орнын анықтау тәсілдері: симметриялық пайдалану, қарапайым бөліктерге жіктеу, теріс массалар тәсілі. 4. Жазық фигуралардың статикалық моменттері мен оның ауырлық центрі 5. Ауырлық центр. Кейбір фигуралардың ауырлық центрларының орыны.

Ауырлық центрі

Ауырлық центрі немесе Масса центрі - жүйені қозғалтқан кезде жүйенің барлық массасы жинақталған материалдық нүкте сияқты қозғалатын механикалық жүйедегі массаның таралуын сипаттайтын нүкте, қатты дененің кеңістіктегі кез келген қалпында оның бөлшектеріне тең әсерлі күшпен түсетін ауырлық күшінің геометриялық нүктесі; бұл нүкте кей жағдайда осы дененің ешбір нүктесімен сәйкес келмеуі мүмкін (мысалы, сақинада) . Біртекті ауырлық өрісіндегі қатты дененің ауырлық центрі оның массалар центріне сәйкес келеді. Денені салмақтары p ₁ , p ₂ , . . . , pn болатын бөліктерге бөліп, олардың ауырлық центрі лерінің (х ₁ , у ₁ , z ₁ ), (x ₂ , y ₂ , z ₂ ), . . . координаттары арқылы, сол дененің ауырлық центрінің координаттарын (х _с , у _с , z _c ) мына формуламен анықтауға болады: X _c = (p ₁ x ₁ + p ₂ x ₂ + . . . pnxn) / (p ₁ + p ₂ + . . . pn)
Y _c = (p ₁ y ₁ + p ₂ y ₂ + . . . pnyn) / (p ₁ + p ₂ + . . . pn)
Z _c = (p ₁ z ₁ + p ₂ z ₂ + . . . pnzn) / (p ₁ + p ₂ + . . . pn) Симметрия центрі бар біртекті дененің (тікбұрышты немесе дөңгелек пластина, шар, цилиндр, куб т. б. ) ауырлық центрі сол дененің симметрия центрінде жатады.

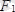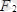Параллель күштер центрі Кеңістікте бір жаққа қарай бағытталған параллель күштер дененің нүктелеріне қойылған болсын (7. 2 сурет) . Күштер қойылған нүктелердің радиус векторларын сәйкес деп белгілейік. Жоғардағы тақырыпқа негізделіп, әуелі және күштерін қоссақ:

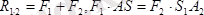
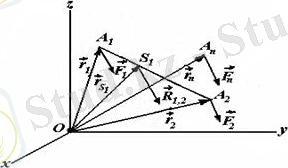7. 2 сурет S ₁ нүктенің радиус-векторын 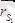десек, онда 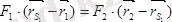Бұл өрнектен 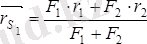келіп шығады. Әрі қарай қосуды жалғастырсақ:

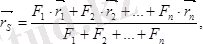
немесе 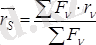(7. 5) болады. (7. 5) формула көмегімен анықталатын S нүкте параллель болған күштер центрі (орталығы) делінеді.

Қатты дененің ауырлық центрі. Дененің ауырлық центрінің координаттары. Ауырлық центрінің орнын анықтау тәсілдері: с имметриялық пайдалану, қарапайым бөліктерге жіктеу, теріс массалар тәсілі.

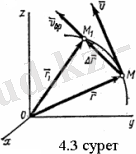
Дененің А ₁ , A ₂ нүктелерінде түсетін екі параллель 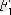және 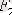күштерін қарастырайық (3. 5 сурет) . 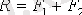тең әсерлі күшінің әсер ету сызығы қосылатын күштерге параллель және A ₁ A ₂ түзуінде жатқан С нүктесінен өтеді. С нүктесінің орнын Вариньон теоремасын қолданып анықтай аламыз: 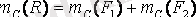, осыдан 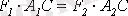. (3. 13), күштерін А ₁ , А ₂ нүктелерінің айналасында бірдей α бұрышына бұрғанда, тең әсерлі күші де сол бағытта α бұрышына бұрылады және дәл сол С нүктесіне түседі. С нүктесі п араллель күштердің центрі деп аталады. Кез келген күштер саны үшін де осылай болады. 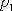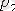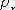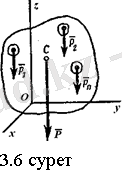Дене бөлшектеріне түсетін , , …, ауырлық күштерінің тең әсерлісін деп белгілейік (3. 6 сурет) . Осы күштің модулі дененің салмағы деп аталады және келесі теңдікпен анықталады (3. 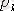14) С нүктесі параллель ауырлық күштерінің центрі болып келеді, ол дененің ауырлық центрі деп аталады. Сонымен, АҚД-нің ауырлық центрі - денемен өзгеріссіз байланысқан дененің кеңістікте кез келген орналасуында дене бөлшектеріне түсетін ауырлық күштерінің тең әсерлі күшінің әсер ету сызығы өтетін нүкте. Ауырлық центрінің координаттары келесі формулалармен анықталады 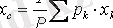, , 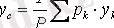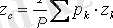(3. 15)

мұндағы , , 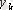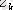- ауырлық 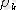күштері түсетін нүктелердің координаттары.

Жазық фигуралардың статикалық моменттері мен оның ауырлық центрі

К 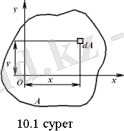ейбір жазық фигураны x , y координат жүйесінде қ 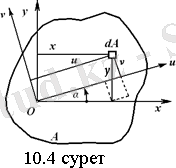арастырайық (10. 1 сурет) . Келесі интег-ралдар 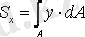, 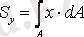( 10. 1) фигураның сәйкес x және y өстеріне қатысты ста-тикалық моменттері деп аталады. Координаттық өстерді параллель орын ауыс-тырса, қиманың статикалық моменттері қалай өзге-ретінін анықтайық (10. 2 сурет ) . x ₂ = x ₁ - a; y ₂ = y ₁ - b болатыны анық. Сонда 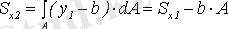, 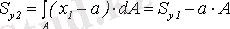. А мен b шамалары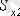н, мен 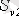стати-калық моменттері нөлге тең болатындай, таңдап алуға болады (тек бір ғана ретімен) . Центрлік өс деп оған қатысты статикалық момент нөлге тең болатын өсті атайды. Центрлік өстерінің қиылысу нүктесі қиманың ауырлық центрі деп аталады. ( x ₁ , y ₁ ) координат жүйесінде ауырлық центрінің координаттары осыған тең 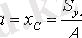, 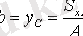. (10. 2)

Құрама қиманың статикалық моменті оны құраушы аймақтарының статикалық моменттерінің қосындысына тең екенін айтып өтейік. Қиманың Х, У өстеріне қарағандағы статикалық моменттері деп төмендегі интегралдармен анықталған геометриялық сипаттамаларды айтамыз:

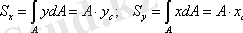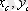, мұндағы шексіз кіші аудан; х, у шексіз кіші ауданның координаттары; А қиманың ауданы; қиманың ауырлық центрінің координаттары.

Ауырлық центр. Кейбір фигуралардың ауырлық центрларының орыны.

Дененің жерге тартылу күшін дененің ауырлық күші деп, ал сол ауырлық күшінің түсу нүктесін дененің ауырлық ценрті деп атаймыз. Егер, дене бірнеше күрделі бөлшектерден тұратын болса, онда денені ойша элементар бөлшектерге бөліп қарастырамыз, оның әрбір бөлшегіне вертикаль төмен бағытталатын және бөлшектің центріне түсірілетін ауырлық күштері әсер етеді. Дене өлшемдері жер радиусынан әлдеқайда аз болғандықтан, дене бөлшектеріне әсер ететін ауырлық күштерін тұрақты және біріңғай параллель бағытталған күш деп есептейміз. Бөлшектердің ауырлық күштерінің тең әсер етуші күші 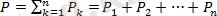дененің ауырлық күші, ал осы параллель күштер жүйесінің С центрі дененің ауырлық центрі деп аталады. Денені кез-келген бағытта бұрғаннан дене бөлшектерінің 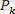ауырлық күштері түсірілген нүктелер орнын өзгертпейді. Сондықтан денені кез-келген бағытта бұрғанннан дененің ауырлық центрінің орны өзгермейді. Дененің ауырлық центрінің орынын анықтау үшін параллель күштер жүйесінің центрін анықтайтын теңдіктерді қолданамыз.