Қос күш. Бас векторы және бас моменті

Пән: Физика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 8 бет
Таңдаулыға:

Мәнжазба

Тақырыбы: Қос күш. Бас векторы және бас моменті. Күштер жүйесінің тепе-теңдік шарты.

2015

Жоспар:

1. Қос күш 2. Кеңістіктегі кез келген күштер жүйесінің тепе-теңдік шарттары. Параллель күштер 3. Күштер жүйесінің тепе-теңдік шарты 4. Бас векторы және бас моменті 5. Күштің түсінігі. Күштің оське проекциясы. Жазық жүйедегі жинақталатын күштер. 6. Күшті берілген центрге келтіру 7. Кез-келген күштер жүйесін берілген центрге келтіру 8. Кез-келген күштер жүйесін қарапайым түрге келтіру 9. Кез-келген күштер жүйесінің тепе-теңдік шарттары 10. Күштің нүктеге қатысты моменті

Қос күш - қатты денеге =-P), өзара¢әсер ететін, шамалары тең, бағыттары қарама-қарсы (P параллель екі күштің жүйесі . Қос күш өзі түскен денені айналдыруға тырысады. Оның тең әсерлі күші болмайды. Қос күштің қатты денеге әсер ететін сызықтарының арақашықтығы оның иіні (l), ал Қос күштің денеге әсерін сипаттайтын векторлық физикалық шама Қос күштің моменті (М) деп аталады: M=[Рxl] . Қос күштің шамасы мен иінін өзгерткенде оның моменті (M) тұрақты болса, онда Қос күштің денеге әсері де тұрақты болады. Сондықтан Қос күштің моменті (M) еркін вектор болып есептеледі; оны дененің кез келген нүктесіне түсіруге болады. Бір денеге түсірілген, моменттері бірдей (M1=M2) екі Қос күш бір-біріне механикалық эквивалентті болып табылады. Кез келген жүйенің Қос күштерінің моменттерінің геометриялық (векторлық) қосындысы нөлге тең болса, ондай жүйе теңгерілген жүйе деп саналады.

Кеңістіктегі кез келген күштер жүйесінің тепе-теңдік шарттары. Параллель күштер Кеңістіктегі кез келген күштер жүйесінің тепе-теңдігінің қажет және жеткілікті шарттары векторлық түрде мына теңдіктермен өрнектеледі:

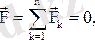
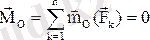Бірақ пен 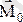векторлары тек 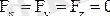және 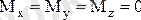болғанда ғана нөлге тең. Сондықтан күштердің мынандай аналитикалық тепе-теңдік шарттарын аламыз:

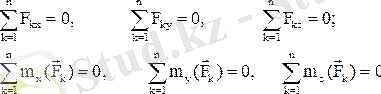(1. 7. 5)

Сонымен, кеңістіктегі кез келген күштер жүйесі тепе-теңдікте болу үшін барлық күштердің координата өстерінің үшеуіне проекцияларының қосындысы мен олардың осы өстерге қатысты моменттерінің қосындысы нөлге тең болуы қажет және жеткілікті.

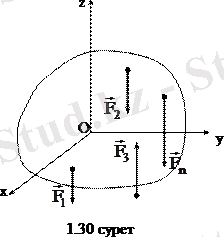1. 7. 5) теңдеулер сонымен қатар кеңістіктегі кез келген күштер жүйесі әсер ететін қатты дененің тепе-теңдік шарттары болады. Олардың бірінші үш теңдеуі дененің өстер бойымен жылжымайтындығының, cоңғы үш теңдеуі өстерді айнала алмайтындығын сипаттайды. Денеге күштермен бірге моменті 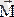қос күш әсер етсе, оның моменті соңғы үш теңдеуге қосылады. Егер денеге әсер ететін күштердің бәрі өзара параллель болса, онда бір өсті, мысалы өсін күштерге параллель етіп алуға болады (1. 30 сурет) . Сонда күштердің әрқайсысының х пен у өстеріне проекциялары және олардың z өсіне қатысты моменттері нөлге тең болады. Олай болса параллель күштердің тепе-теңдік шарттары қалған үш теңдеумен беріледі (басқа теңдеулер 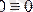түріндегі теңбе-теңдікке айналғандықтан) : 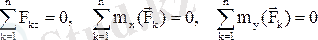(1. 7. 6)

Демек, кеңістіктегі параллель күштер жүйесі тепе-теңдікте болу үшін барлық күштердің осы күштерге параллель өске проекцияларының қосындысы мен олардың қалған екі өске қатысты моменттерінің қосындысы нөлге тең болуы қажет және жеткілікті. Есеп шығарғанда тең әсерлі күштің моменті туралы Вариньон теоремасы күштің өске қатысты моментін анықтауды жеңілдетеді. Себебі, моменті анықталатын күшті құраушыларға жіктесек, онда осы құраушылардан кез келген өске қатысты момент алу қиын болмайды. Күштер жүйесінің тепе-теңдік шарты . Бұл үшін бас вектор мен бас моменті кез келген нүктеге қатысты нольге болу қажет: R = о, M ₀ = о. Бас векторы және бас моменті Сырғанақ векторлар әсіресе механикада пайдаланылады. Механикадағы ең қарапайым мысал - күш. Өзі жатқан түзу бойымен вектор бас нүктесін көшіргенмен қай нүктеге қатысты есептесе де күш моменті өзгермейді; керісінше, басын басқа түзуге көшірсе тіпті вектордың бығыты мен ұзындығын сақтағанның өзінде күш моменті әрдайым дерлік өзгереді: сондықтан күшті еркін вектор ретінде санауға болмайды. Бас вектор мен бас моменттің а нықтамасы бойынша бас вектор барлық күштердің геометриялық қосындысы, ал бас момент барлық күштердің О нүктесіне қатысты моменттерінің геометриялық қосындысы. Кеңістіктегі кез келген күштер жүйесі үшін бұл екі вектор декарттық координата жүйесінің үш өсіне проекцияланады: 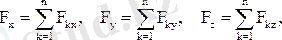(1. 7. 3) 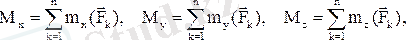(1. 7. 4)

Жазықтықтағы кез келген күштер жүйесі үшін де бас вектор барлық күштердің геометриялық қосындысы болады және декарттық координаталар жүйесінің екі өсіне проекцияланады: . (1. 5. 3) Бас вектордың сан шамасы (модулі) мына өрнекпен анықталады: , (1. 5. 4) ал бағыты бағыттаушы косинустардың көмегімен анықталады: 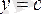(1. 5. 5) Бұл жағдайда да О нүктесіне қатысты бас момент барлық күштердің О нүктесіне қатысты моменттерінің алгебралық қосындысы болады: 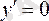. (1. 5. 6) Егер денеге күштермен қатар қос күштер әсер етсе, олардың моменттері жүйенің бас моментіне қосылады.

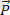Күштің түсінігі. Күштің оське проекциясы. Жазық жүйедегі жинақталатын күштер. Статика есептерін аналетикалық әдіспен шешу кезінде күштің оське проекциясы туралы ұғым кеңінен қолданылады. Денеге кез-келген күші әсер етсін делік. Осы күш векторының Х және Y осьтеріне проекцияларын анықтау үшін күш векторының басынан және ұшынан осьтерге перпендикулярлар жүргіземіз, осы Х және Y осьтерінің бойында пайда болған 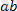және 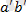кесінділері 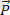күшінің Х және Y осьтеріне проекциялары 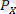және 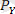деп аталады.

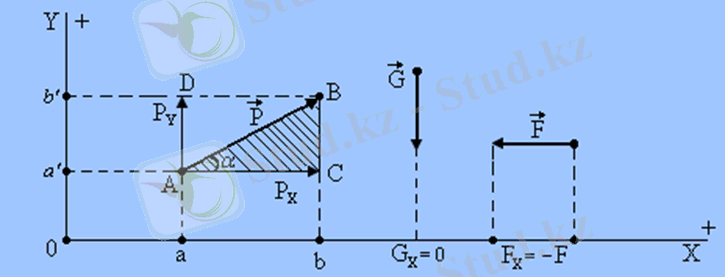2. 1-сурет. Күштің оське проекциясы.

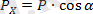
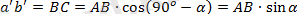ABC үшбұрышынан: немесе немесе 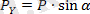Ендеше, күштің оське проекциясының шамасы күштің шамасын, күш пен осьтің арасындағы бұрыштың косинусының көбейтіндісіне тең, егер күш векторының бағыты координат жүйесінің оң бағытымен сәйкес келсе проекция оң шама, ал егер сәйкес келмесе теріс шама болады. Бұл жағдайда 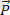күші, 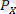және 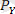күштерінің теңәсер етуші күші болып табылады және оның шамасы 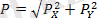формуласымен анықталады. Егер, күштер жүйесінің әсер ету түзулері бір нүктеде қиылысып және барлық күштер бір жазықтықта орналасса ондай күштер жазықтықтағы жинақталған күштер жүйесі деп аталады. Жазықтықтағы жинақталатын күштер жүйесінің теңәсер етуші күшін аналитикалық және геометриялық тәсілдер бойынша анықтауға болады:

Күшті берілген центрге келтіру Әсер сызықтары кеңістікте (жазықтықта) кез-келген түрде орналасқан күштерден құралған жүйе кеңістіктегі (жазықтықтағы) кез-келген күштер жүйесі делінеді. Кез-келген күштер жүйесі әсеріндегі дене жағдайын немесе тепе-теңдігін зерттеу үшін осы күштер қарапайым түрге келтіріледі. Пуансо леммасы. Күшті бір нүктеден берілген центрге келтіру нәтижесінде келтіру центрінде осы күшке тең болатын күш және оның қосылған жұбы алынады. Дәлелі. Айталық, дененің А нүктесіне 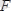күш қойылған болсын (5. 1 сурет) . Бұл күшті кезкелген О нүктеге параллель көшіру үшін 3 аксиомаға 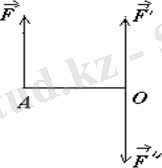сәйкес осы нүктеге 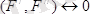күшті қоямыз (5. 1 сурет) . Мұнда . Нәтижеде: 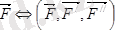, немесе 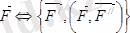. 5. 1 сурет Мұндағы 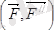қосылған жұп делінеді. Осы күштің моменті (4. 2) -ге сәйкес төмендегідей болады:

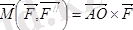немесе 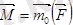. Демек: 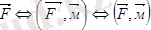. Осымен лемма дәлелденеді.

Кез-келген күштер жүйесін берілген центрге келтіру Айталық, денеге 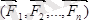күштер қойылған болсын. Жоғарыдағы тақырыпқа негізделіп, Пуансо леммасын қолданамыз (5. 2 сурет) .

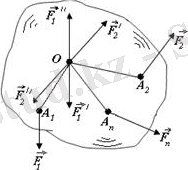
5. 2 сурет. 5. 3 суретНәтижеде О нүктеде 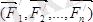күштер және 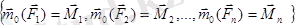қосылған жұптар пайда болады. Егерде күштердің әсер сызықтары кеңістікте болса, жұп моменттерінің векторлары геометриялық; жазықтықта болса, алгебралық қосылады. күштер қиылысатын күштер жүйесі болғандықтан олар геометриялық қосылады. Нәтижеде: 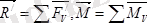(5. 1)

Мұнда 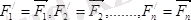болғандықтан (5. 1) -ді төмендегідей жазу мүмкін: 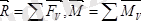(5. 2)

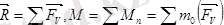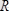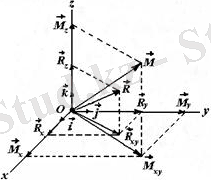
Кезкелген күштер жүйесі жазықтықта орналасқан болса, (5. 2) -ні былай жазамыз: (5. 3) (5. 2) және (5. 3) өрнектердегі күштер жүйесінің бас векторы, ал 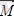бас моменті делінеді. Демек, кезкелген күштерді берілген центрге келтіру нәтижесінде бір бас вектор және бір бас момент алынады (5. 3 сурет) . Бас вектор және бас моментті аналитикалық тәсілде төмендегідей есептеу мүмкін. 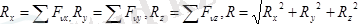(5. 4Бас вектор мен бас момент арасындағы бұрышты анықтау үшін бұл векторларды скаляр көбейтеміз: 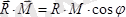. Немесе 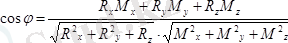(5. 6) келіп шығады.