Математикалық логика және дискретті математика: жоғары оқу орындарына арналған оқулық


Қазақстан Республикасының білім және ғылым министрлігі
Қ. Жетпісов
МАТЕМАТИКАЛЫҚ ЛОГИКА ЖӘНЕ
ДИСКРЕТТІ МАТЕМАТИКА
Қазақстан Республикасы Білім және ғылым
министрілігі оқулық ретінде бекіткен
Алматы, 2011
ӘОЖ 510 (075. 8)
ББЖ 22. 12 я73
Ж 56
Пікір жазғандар:
Е. С. Смаилов - «Қолданбалы математика институты» Республикалық мемлекеттік қазыналық кәсіпорынның директоры ф. -м. ғ. д., профессор;
У. У. Өмірбаев - Л. Н. Гумилев атындағы Евразия ұлттық университе-тінің алгебра және геометрия кафедрасының меңгерушісі ф. -м. ғ. д., профессор;
Қ. Оспанов - Л. Н. Гумилев атындағы Евразия ұлттық университетінің есептеу және қолданбалы математика кафедрасының профессоры, ф. -м. ғ. д. .
Жетпісов Қ.
Ж 56 Математикалық логика және дискретті математика: оқулық жоғары оқу орындарының студенттеріне арналған. - Алматы: ЖШС РПБК «Дәуір», 2011. - 264 бет.
ISBN 978-601-217-186-0
Оқулық математикалық логика, дискретті математика атты екі бөлімнен тұрады.
Математикалық логика бөлімінде жиындар теориясының элементтері, тұжырымдар алгебрасы мен тұжырымдар санағы, предикаттар санағы мен алгебралық жүйелер туралы айтылады. Бұл бөлімде математикалық логиканың негізгі теоремалары дәлелденген. Атап айтқанда, Левенгейм-Сколем теоремасы, Гедель теоремасы, Мальцевтің локальдық теоремасы т. т.
Дискретті математика бөлімінде графтар теориясының негіздері, кодтау теориясының элементтері, логикалық желілер мен ақырлы автоматтар туралы баяндалады.
Оқулық университеттердің «математика», «информатика», «ақпараттық жүйелер» мамандықтары бойынша білім алушы студенттерге арналған.
ISBN 978-601-217-186-0
Ж
© Жетпісов Қ., 2011 ж.
© ҚР Жоғары оқу орындарының
қауымдастығы, 2011 ж.
Алғы сөз
Математикалық логика және дискретті математика оқулығы екі бөлімнен тұрады.
Оқулықтың бірінші бөлімі - математикалық логика. Ол автордың Х. Дулати атындағы Тараз мемлекеттік университетінің ақпараттық жүйелер кафедрасының доценті Ж. А. Түсіповпен бірлесіп жазған 2000 жылы жарық көрген «Математикалық логика» оқу-құралының негізінде жазылған.
Онда қарастырылған мәселелер: жиындар теориясына кіріспе, тұжырымдар алгебрасы, тұжырымдар санағы, предикаттар санағы, алгебралық жүйелер және модельдер теориясына кіріспе.
Модельдер теориясына кіріспе тарауында теоретикалы-модельдік алгебра мен предикаттар санағы тілінің арасындағы байланыстар туралы алғашқы мағлұматтар берілген.
Атап айтқанда, элементар ішкі модель, элементар эквивалентті және изоморфты модельдер, модельдің диаграммалары, алгебралық жүйелердің элементар тізбегі қарастырылған.
Алгебралық жүйелер тарауында предикаттар санағының негізгі теоремалары толығымен дәлелденген.
Оқулықтың екінші бөлімі үш тараудан тұрады.
Графтар теориясының негіздері деп аталатын алтыншы тарауда графтар мен оның бөліктері, элементтері (тізбек, жол, цикл және контур) бөлікті графтар, ішкі графтар, графтарда анықталған амалдар мен қатынастар, графтардың сыбайластық және инциденттік матрицалары, графтың дәрежесі, эйлерлік және гамильтонды графтар, графтағы ең қысқа жолды табу алгоритмі сияқты сұрақтар қарастырылған. Кодтау теориясының элементтері тарауында әріптік және сандық кодтаулар, тиімді кодтау, қателерді ажырататын және түзететін кодтар, Хеминг коды туралы айтылған.
Әріптік кодтардың мысалы ретінде Морзе коды келтірілген.
Логикалық желілер және автоматтар атты сегізінші тарауда Буль функциялары арқылы анықталған функционалдық сызбалар, логикалық желілер, автоматтардағы периодты тізбектер туралы мағлұматтар берілген.
Әрбір тараудың соңында мысалдар келтіріліп, есептер мен жаттығулар берілген.
Көптеген есептердің шығару тәсілдері көрсетілген.
Оқулықта байқалған кемшіліктер болса және басқа да тілектеріңізді Е. А. Бөкетов атындағы Қарағанды мемлекеттік университетінің математика факультетінің Т. Ғ. Мұстафин атындағы алгебра, математикалық логика және геометрия кафедрасына жолдауларыңызды сұраймын.
МАТЕМАТИКАЛЫҚ
ЛОГИКА
I. ЖИЫНДАР ТЕОРИЯСЫНЫҢ ЭЛЕМЕНТЕРІ
II. ТҰЖЫРЫМДАР АЛГЕБРАСЫ
IІI. аксиомалық Әдіс. санақ.
ІV. ПРЕДИКАТТАР САНАҒЫ
V. АЛГЕБРАЛЫҚ ЖҮЙЕЛЕР
I ТАРАУ
ЖИЫНДАР ТЕОРИЯСЫНЫҢ ЭЛЕМЕНТТЕРІ
Жиындар теориясының негізі XIX ғасырда Кантор еңбектерінде құрылған. Оған негізгі себеп математикалық талдауды құру және негіздеу проблемасы болды. Әріректе, осы математикалық талдау берген алғашқы серпін мен оның негізгі концепицяларының дамуы және оларды талдау мен қатаң түрде ұғынудың қалыптасуы қазіргі заманғы аксиомалық жиындар теориясына негіз болды.
Математиканың дамуына тигізген жиындар теориясының үлкен ықпалы қазіргі заманда барлығымыз мойындаған факт. Сондықтан, жоғарғы оқу орындарында математиканы оқытуда жиындар теориясының идеялары мен әдістерінің маңызды роль атқаратындығы толығымен заңдылық. Жиындар теориясының интуитивті негіздерін жүйелі оқып-зерттеу кез келген қазіргі заманғы математикалық пәндерді табысты оқып-зерттеудің айрылмас құраушысы болып табылады.
Бұл тараудың негізгі оқып-зерттеу объектісі теоретикалы-жиындық амалдар мен қатынастар және сонымен қатар олармен байланысты қарапайым құрылымдар болып табылады.
Материалды баяндау жиын ұғымы туралы көріністі интуитивті ұғыну негізінде іске асырылады.
Алғашқы ұғым ретінде жиын ұғымымен қатар
 элементінің
элементінің
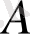 жиынына тиісті болу қатынасы ұғымы пайдаланылады (
жиынына тиісті болу қатынасы ұғымы пайдаланылады (
 ) . Жиын өзінің элементтерімен толығымен анықталады деген қағиданы ұстанып жиынды берудің (жиынның берілуінің) айқын әдісімен қатар шыршықтау принципіне негізделген әдісті пайдаланамыз.
) . Жиын өзінің элементтерімен толығымен анықталады деген қағиданы ұстанып жиынды берудің (жиынның берілуінің) айқын әдісімен қатар шыршықтау принципіне негізделген әдісті пайдаланамыз.
Жиынды әртүрлі әдістермен анықтай отырып, біз алдын-ала оның ең болмағанда бір элементінің болатындығы туралы айта алмаймыз. Осы себепті, бос жиын ұғымын енгізу қажеттілігі туындайды. Алдағы уақытта, элементтің жиынға тиісті болу термині ұғымында қамтылу қатынасы мен жиындардың теңдігі енгізіледі. Ал бұлар содан соң жиындардың теңдігін дәлелдеудің негізгі әдісі ретінде «қамтылу әдісін» негіздеуге және қолдануға көмектеседі.
Бұл ұғымдарды енгізу процесінде
 ;
;
 ;
;
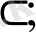
 қатынастарының арасындағы айрықша ерекшеліктерге ерекше көңіл аударылады.
қатынастарының арасындағы айрықша ерекшеліктерге ерекше көңіл аударылады.
Теоретикалы-жиындық амалдар
 ;
;
 ; \ - бірігу, қиылысу, айырма жаңа жиындарды құрудың әдістері ретінде пайдаланылады және әріректе, ешқандай проблемасыз аксиомалық жиындар теориясын оқып-зерттеуге көшуге көмегін тигізеді. Бұл сонымен қатар, берілген жиынның ішкі жиындарының жиынын алу және реттелген пар жиындарды алу амалдарына да қатысты. Теоретикалы-жиындық амалдардың қасиеттері қос-қостан топталады. Бұл
; \ - бірігу, қиылысу, айырма жаңа жиындарды құрудың әдістері ретінде пайдаланылады және әріректе, ешқандай проблемасыз аксиомалық жиындар теориясын оқып-зерттеуге көшуге көмегін тигізеді. Бұл сонымен қатар, берілген жиынның ішкі жиындарының жиынын алу және реттелген пар жиындарды алу амалдарына да қатысты. Теоретикалы-жиындық амалдардың қасиеттері қос-қостан топталады. Бұл
 және
және
 бірігу және қиылысу амалдарының қосалқылық сипатын көрсетеді және ол жиындар алгебрасында және басқа да математикалық жүйелерде «қосалқылық заңын» ұғынудың пропедитивті негіздерін қалайды.
бірігу және қиылысу амалдарының қосалқылық сипатын көрсетеді және ол жиындар алгебрасында және басқа да математикалық жүйелерде «қосалқылық заңын» ұғынудың пропедитивті негіздерін қалайды.
Универсал жиынның кейбір ішкі жиындарының арасында орын алуы мүмкін қарапайым қатынастар мен тәуелділіктерді графиктік кескіндеу үшін Эйлер-Венн диаграммасы қолданылады.
Универсал жиынның кейбір
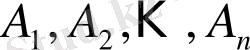 ішкі жиындарынан құрылған күрделі өрнек үшін оларға
ішкі жиындарынан құрылған күрделі өрнек үшін оларға
 ;
;
 ; \ амалдарын бірнеше қайтара (бірақ ақырлы рет) қолдану арқылы Эйлер-Венн диаграммасы қарапайым қатынастар мен тәуелділіктерге сәйкес келуші диаграммаларды топтастырудың көмегімен құрылады және ол күрделі өрнек құрайды.
; \ амалдарын бірнеше қайтара (бірақ ақырлы рет) қолдану арқылы Эйлер-Венн диаграммасы қарапайым қатынастар мен тәуелділіктерге сәйкес келуші диаграммаларды топтастырудың көмегімен құрылады және ол күрделі өрнек құрайды.
Мұндай диаграмаларды құру процесінде интуитивті деңгейде жиындар теориясының формулалары мен ішкі формулалары ұғымдары енгізіледі. Бұл алдағы уақытта, формальді тіл мен логикалық санақтың дедуктивті құралдарын анықтаудың базалық процедуралық негізгі ретінде индуктивті әдісті қолданудың ерекшеліктерін түсінуде басты роль атқарады.
Екі жиынның декарттық көбейтіндісін енгізудегі жұмыста бастапқы нүкте ретінде жазықтықтағы тік бұрышты декарттық координаталар жүйесі концепциясы алынады.
Жиындардың берілуінің алдыңғы (ертеректе) келтірілген әдісіне қосымша ретінде екі ақырлы жиынның декарттық көбейтіндісін сипаттаудың кестелік әдісі мен график арқылы оның көрнекі берілу әдісі беріледі. Осыдан кейін, мысал арқылы
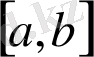 кесіндідегі үзіліссіз
кесіндідегі үзіліссіз
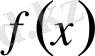 функциясының графигі мен
функциясының графигі мен
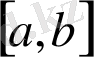 және
және
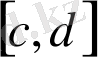 жиындарының декарттық көбейтіндісі
жиындарының декарттық көбейтіндісі
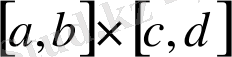 -ның графигінің арасындағы айырмашылықтары мен ұқсастықтары көрсетіледі, мұндағы
-ның графигінің арасындағы айырмашылықтары мен ұқсастықтары көрсетіледі, мұндағы
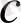 және
және
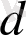 сандары
сандары
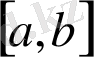 кесіндісіндегі осы функцияның, сәйкесінше, ең үлкен және ең кіші мәндері.
кесіндісіндегі осы функцияның, сәйкесінше, ең үлкен және ең кіші мәндері.
Бірнеше жиындардың декарттық көбейтіндісін табу үшін анықтаудың индуктивті әдісі қолданылады.
Оқытудың мазмұндық негіздеу концепциясының қарарларын іске асыра отырып, бұл тарауда, жаңа декарттық көбейтінді амалын енгізуге байланысты, негізгі амалдардың қасиеттерін анықтаумен қатар оның негізгі
 ;
;
 ; \ амалдарымен үйлесімді қасиеттерін анықтау сұрақтары туындайды.
; \ амалдарымен үйлесімді қасиеттерін анықтау сұрақтары туындайды.
Сонымен, ертеректе енгізілген ұғымдардың мазмұндық өрісінің тармақталу процесінде оларды жаңа мазмұндармен толықтыру мүмкіндіктері қолданылады.
Мұндай тәсілдің өміршеңдігін атай отырып, жұмыста әдістемелік сипаттағы келесі қарарлар тұжырымдалады (универсал қолдануға ие) :
а) Жаңадан еңгізілген ұғымдардың басқа да, ертеректе анықталған ұғымдармен байланысын және ерекшеліктері мен қасиеттерін анықтау. Бұл жаңа ұғымдарға нақты ажыратушы белгілер береді және олар белгілі бір контексте пайда болған жағдайда оларды тануға, ажыратуға көмектеседі.
б) Жаңа ұғымдармен тікелей жұмыс (олардың ең қарапайым түрінде) математикалық пәндерді оқып-зерттеудің фрагменттік шеңберінде, бұл ұғымдардың әртүрлі байытылу мен трансформациялар ерекшеліктерін қолдануда өзіндік (қалыптасу) үйрену дайындығы және бұл ұғымдардың қазіргі заманғы математика мен оның қосымшаларындағы әртүрлі облыстары болып табылады. Жиындардың декарттық көбейтіндісінен сәйкестіктерге, олардың берілу тәсілдері мен оларға қолданылатын амалдарға көшу табиғи түрде орындалады. Ақырлы сәйкестіктер, декарттық көбейтіндінің ішкі жиыны ретінде бағдарланған графтар мен қималар арқылы да берілуі мүмкін.
Сонымен, ұғымдарды байыту өзінен кейін тікелей оларды мазмұндық ұғынумен, сезінумен қатар жүретін байыту мүмкіндігі. Сондықтан оны сипаттық суреттерде, сызбаларда, графиктерде және басқа да геометриялық сипаттағы баламаларда іске асырған дұрыс. Бұл үшін, сәйкестіктердің берілу тәсілдеріне байланысты материалдар үлкен мүмкіндік береді.
Сәйкестік ұғымы белгілі теоретикалық-жиындық амалдар мен декарттық көбейтінді амалынан басқа тағы екі амал енгізуге мүмкіндік береді: кері сәйкестік алу амалы мен сәйкестіктерді көбейту (композиция) амалы. Бұл «амалдар» ұғымын тармақтауға кезекті қадам жасауға жол ашады.
1. 7 параграфында жоғарыда келтірілген әдістемелік сипаттағы а), б) қарарларын іске асыру аясында жаңа амалдардың қасиеттері анықталады. Тарауды жиындар теориясының ең бір маңызды ұғымы - «бейнелеу» ұғымын аяқтайды. Мұнда алдымен тікелей осы ұғымның анықтамасы беріледі, (мектептік функционалдық көріністі іске асырушы), ал сонан соң кері бейнелеуді алу амалы мен бейнелеулердің көбейтіндісі тілінде оның сипаттамасы беріледі. Сонан соң осы екі анықтамалардың теңқуаттылығы дәлелденеді. Әдістемелік деңгейде осыған ұқсас дәлелдеулерден алынатын тәжірибе формальды аксиомалық теориялар әдісін меңгеруде қажетті кезең болып табылады. Себебі, олар мазмұндық қорытынды шарттарын құрумен байланысты болады. Мұнда ұғым бір қатынастар жүйесінде (осы ұғымды беруші шарттардан), бірақ олар басқа қатынастар жүйесінің тілінде тұжырымдалған.
1. 8 параграфында «атомдық» бейнелеулердің ерекше рөлі атап өтіледі.
Олар: сюръекция, биекция, инъекция және олардың көмегімен сәйкес композициялардың көмегімен алынатын, атомдардан құрылған молекула сияқты, кез келген бейнелеу.
«Алгебралық амал» ұғымы «алгебралық жүйе» ұғымының негізгі құраушысы ретінде өзінің маңыздылығын жан жақты ұғынуды талап етеді. Бұл тарауда «амал» ұғымының тура интуитивті мағыналық көрінісінен аксиомалар жүйесі түрінде абстракциялы берілу жолының кезеңдерін қадағалайтын боламыз.
Басты назарды бинарлық және унарлық (екі орынды және бір орынды) амалдарға аударамыз.
Себебі, олар жоғарғы оқу орындарында оқып, зерттелетін классикалық алгебралық жүйелердің негізгі амалдарының санына енеді.
Бұл тараудың материалдарын баяндау сандық жиындарда анықталған мектептегі әріптік алгебра мен онда анықталған арифметикалық (рационал) амалдарға алғашқы саяхаттан басталады. Осыдан кейін абстракциялық жиында берілген алгебралық амалдар концепциясына байланысты анықтамалар мен ұғымдар жүйесін оқып-зерттеуге көшеміз.
Жұмыс барысында бұл процесті іске асыру алдымен рационал сандарға негізделген, ал содан кейін нақты сандарға негізделген бірнеше ғасырлық (көпғасырлық) практиканың екендігін бірнеше қайтара атап өтіп отырамыз.
Екі орынды амалдардың аксиомалық берілуінің қасиеттерін мектептен белгілі, формальды әріптік теңдіктердің арифметикалық амалдарының заңдылықтары ретінде өрнектелуінен шыққандығын айта кетуге болады. Бинарлық алгебралық амал ұғымын анықтауға жетелеуші көптеген анықтамалардың мағыналық кері бейнесінің баламалары болып кәдімгі қосу, көбейту, алу, бөліктік амал бөлу және олардың қарапайым қасиеттері болып табылады. Алгебралық жүйелер класын абстрактілі сипаттауға (қатысты) байланысты қойылатын мақсаттың бірі ретінде қарастырылып отырған класта анықталған жүйенің негізгі амалдары мен қатынастарының қасиеттерін беруші тиімді аксиомалар жиынтығын таңдау болып табылады. Бұл жағдайда, бұл амалдар мен қатынастардың басқа қасиеттері сол сияқты жүйенің құрылымдық қасиеттері толығымен осы таңдап алынған аксиоматика негізінде анықталады, яғни олардыңсалдарлары ретінде алынады.
§1. 1. Жиындар және оларда анықталған қатынастар
«Жиын» ұғымы математикада жиынтықтар, кластар, құрылымдар мен элементтердің (заттардың) көпбейнелері туралы интуитивті көріністерді кеңейтудің нәтижесінде қалыптасты және нәтижесінде жеке өздігінен бар объект ретінде белгілі болды. Жиындар теориясының негізін қалаушы Г. Кантор (1845-1918 ж. ) жиын ұғымын біздің санамызға, интуициямызға тұтас бір объект ретінде анықталатын және бір-бірінен ажыратылатын кез келген жиынтық түрінде енгізді.
Осы тұжырымдауға сәйкес жиындар деп жоғарыда айтылған сипаттамалардың біреуін қанағаттандыратын осындай объектілер құрылымдарын айтуға болады. Бұл қасиетке қойылатын бір ғана талап - ол біздің интуитивті танымымызға (ұғынуымызға) қол жеткізу.
XIX-ғасырдың аяғына дейін жиынның интуитівті концепциясы ешқандай келіспеушілік тудырған жоқ. Осы концепцияның негізінде интуитивті жиындар теориясы құрылды. Бірақ, одан кейініректегі жиындар теориясының даму кезеңінде, жиын ұғымының осындай кең баяндалуы әртүрлі қарама-қайшылықтарды туғызды (жиындар теориясының еш зиянсыз парадокстары) .
Қазіргі уақытта жиындар теориясы аксиомалық негізге орайластырылған (тұрақтандырылған) және осының нәтижесінде белгілі парадокстық (қарама-қайшылықтық) қасиеттерге ие жиындар толық жойылған. Себебі, қасиеттерді таңдауды шектейтін аксиомалар жүйесі арқылы жиынды қалыптастыру негізін құру мүмкін болды. Осыған қарамастан біз, әріректе, жиын ұғымы туралы интуитивті көрініске жүгінетін боламыз, себебі, аксиомалық жиындар теориясын мағыналық ұғыну, (интуитивті теория деңгейінде алынған), әруақытта терең ұғынылған жеткілікті «ұғымдар мен нәтижелер» бар деп ұйғарылады. Сонымен жиын деп белгілі бір ортақ қасиеттері бойынша топтастырылған объектілер жиынтығын (құрылымын) түсінетін боламыз.
Жиын - латын алфавитіндегі үлкен әріптермен, ал оның элементтері осы алфавиттің кіші әріптерімен белгіленетін болады. Бірақ, а-ның А жиынының элементі болатынын таңбалық түрде
а
 А
деп жазамыз.
А
деп жазамыз.
Керісінше жағдайда,
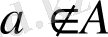 жазуын қолданамыз.
жазуын қолданамыз.
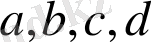 әріптерімен әдетте, жиындардың нақты элементтері белгіленеді. Мысалға
әріптерімен әдетте, жиындардың нақты элементтері белгіленеді. Мысалға
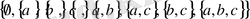 өрнегі
өрнегі
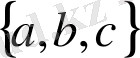 жиының ішкі жиындарының жиыны.
жиының ішкі жиындарының жиыны.
 жиының барлық ішкі жиындарының жиынын
жиының барлық ішкі жиындарының жиынын
 арқылы белгілейміз және
арқылы белгілейміз және
 жиының Булианы деп атаймыз, яғни
жиының Булианы деп атаймыз, яғни
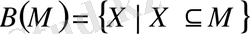
Булиан ұғымына байланысты байқайтынымыз -
 , бірақ
, бірақ
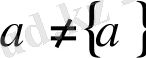 .
.
§1. 2. Жиындардағы амалдар
Барлық жиындар жиынтығында келесі төмендегі анықтамалдарға сәйкес келетін теоретикалық-жиындық 1)
 -қиылысу; 2)
-қиылысу; 2)
 - бірігу; 3) \ - айырма амалдары енгізіледі.
- бірігу; 3) \ - айырма амалдары енгізіледі.
1.
 және
және
 жиындарының қиылысуы
жиындарының қиылысуы
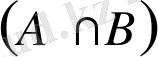 деп бір уақытта осы
деп бір уақытта осы
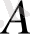 және
және
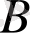 жиындарында жататын элементтерден құрылған жиынды айтамыз, яғни,
жиындарында жататын элементтерден құрылған жиынды айтамыз, яғни,
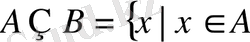 және
және
 .
.
Нақтылы жиындарға
 амалын қолдану мысалдарын келтірейік:
амалын қолдану мысалдарын келтірейік:
а)
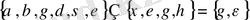 ;
;
б)
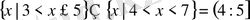 .
.
2.
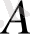 және
және
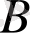 жиындарының бірігуі
жиындарының бірігуі
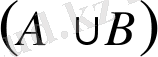 деп осы жиындардың ең болмағанда біреуіне тиісті болатын элементтерден тұратын жиынды айтамыз, яғни,
деп осы жиындардың ең болмағанда біреуіне тиісті болатын элементтерден тұратын жиынды айтамыз, яғни,
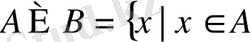 немесе
немесе
 .
.
Мысалға:
а)
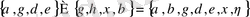 .
.
б) Айталық,
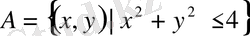 және
және
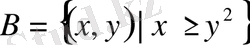
болсын.
1-суретте
 жиынына тиісті
жиынына тиісті
 координаталар жазықтығына тиісті
координаталар жазықтығына тиісті
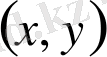 нүктелер жиыны кескінделген.
нүктелер жиыны кескінделген.
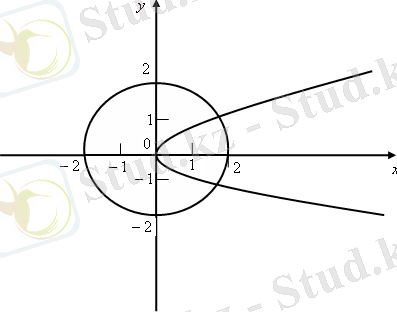
Сурет 1
3.
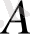 және
және
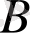 жиындарының айырмасы
жиындарының айырмасы
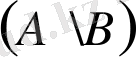 деп
деп
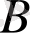 -ға тиісті емес
-ға тиісті емес
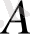 жиының элементтерінен тұратын жиынды айтамыз, яғни,
жиының элементтерінен тұратын жиынды айтамыз, яғни,
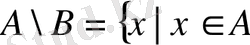 және
және
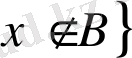 .
.
Сонымен,
 және
және
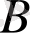 жиындарының айырмасы деп
жиындарының айырмасы деп
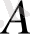 жиынындағы
жиынындағы
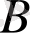 жиынының толығуын айтамыз.
жиынының толығуын айтамыз.
Мысалдар:
а) егер
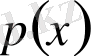 өрнегі жазықтықтағы төртбұрыштың ромб болу қасиетін, ал
өрнегі жазықтықтағы төртбұрыштың ромб болу қасиетін, ал
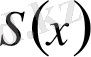 - тіктөртбұрыш болу қасиетін білдірсе, онда
- тіктөртбұрыш болу қасиетін білдірсе, онда
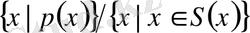 өрнегі барлық шаршы болмайтын ромбтар жиыны;
өрнегі барлық шаршы болмайтын ромбтар жиыны;
в)
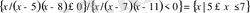 .
.
§1. 3. Теоретикалық-жиындық амалдардың қасиеттері
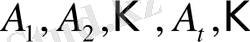 жиындарына
жиындарына
 ,
,
 , \ амалдарын бірнеше қайта қолданудың нәтижесінде қайтадан басқадан жаңа жиындарды аламыз.
, \ амалдарын бірнеше қайта қолданудың нәтижесінде қайтадан басқадан жаңа жиындарды аламыз.
Бұл жиындардың алу процесі - қадамдық сипаттағы индуктивтік
 процесс. Бұл процестегі әрбір қадам, екіншісінен бастап алғанда алдыңғы қадамға кез келген жиынға осы амалдардың кез келгенін бір рет қана қолдану арқылы алынады. Атап айтқанда:
процесс. Бұл процестегі әрбір қадам, екіншісінен бастап алғанда алдыңғы қадамға кез келген жиынға осы амалдардың кез келгенін бір рет қана қолдану арқылы алынады. Атап айтқанда:
0-қадам: Бұл қадамда
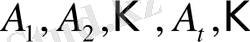 жиындары алынады, яғни негізгі (берілген, бастапқы) жиындар 0-дік қадамның жиындары деп жарияланады.
жиындары алынады, яғни негізгі (берілген, бастапқы) жиындар 0-дік қадамның жиындары деп жарияланады.
Әрі қарай
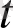 қадамындағы (
қадамындағы (
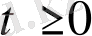 ) барлық жиындар құрылған деп есептеледі және
) барлық жиындар құрылған деп есептеледі және
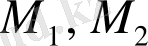 - осы қадамның кез келген жиындары.
- осы қадамның кез келген жиындары.
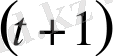 - қадам
:
онда
- қадам
:
онда
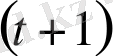 қадамның жиындары деп
қадамның жиындары деп
 қадамының барлық жиындары және
қадамының барлық жиындары және
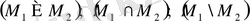
түріндегі жиындар жарияланады.
Осыдан кейін келесі қадамға көшу орындалады.
Мысалы,
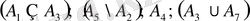 жиындары бірінші қадамда алынса, ал
жиындары бірінші қадамда алынса, ал
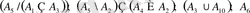 жиындары 2-ші нөмірлі қадамда алынады.
жиындары 2-ші нөмірлі қадамда алынады.
Алгебралық өрнектердегі сияқты жазуды жақшалардың көмегімен теоретикалық-жиындық амалдарды қолдануда да бір мәнді реттеуге болады. Бұл процесті орындау барысында бастапқы жиындардан әртүрлі сипаттағы амалдардың көмегімен алынған, бірақ осыған қарамастан өзара тең болатын жиындарда кездесуі мүмкін. Бұл теоретикалық-жиындық амалдардың сандарда анықталған арифметикалық амалдарға ұқсас белгілі бір анықталған қасиеттерінің бар болуына байланысты болады келеді.
Шын мәнісінде келесі теңбе-теңдіктер орынды:
1)
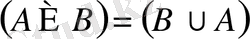 ;
;
2)
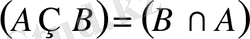 ;
;
3)
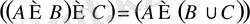 ;
;
4)
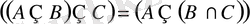 ;
;
5)
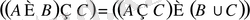 ;
;
6)
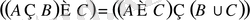 ;
;
7)
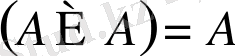 ;
;
8)
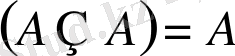 ;
;
9)
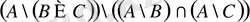 ;
;
10)
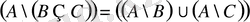 ;
;
11)
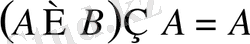 ;
;
12)
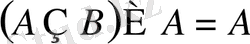 ;
;
13)
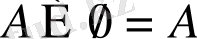 ;
;
14)
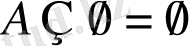 ;
;
15)
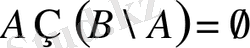 .
.
Бұл теңбе-теңдіктердің барлығы кез-келген
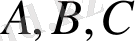 жиындары үшін орынды, яғни жиындар теориясының теңбе-теңдіктері (заңдары) .
жиындары үшін орынды, яғни жиындар теориясының теңбе-теңдіктері (заңдары) .
1) -15) теңбе-теңдіктерді қамтылу әдісін қолданып, оңай дәлелдеуге болады. Осы әдістің 9-теңбе-теңдікті дәлелдеуге қалай қолданылатындығын көрсеттік
Дәлелдеу үшін екі қамтылуды көрсету қажет:
а)
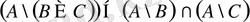 ;
;
б)
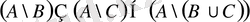 .
.
а) Айталық,
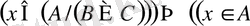 жане
жане
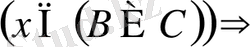
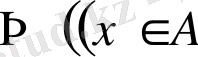 және
және
 және
және
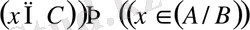
және
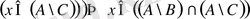 ;
;
б) Айталық
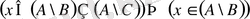 және
және
 және
және
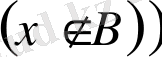 және
және
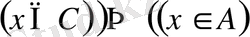 және
және
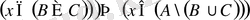 .
.
1) -15) тізіммен теоретикалық-жиындық амалдардың негізгі қасиеттерін көрсететін теңбе-теңдіктер келтірілген. Әрине, бұл тізімге енбеген басқа да теңбе-теңдіктер бар.
§1. 4. Эйлер-Венн диаграммалары
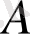 және
және
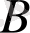 жиындарына теоретикалық-жиындық амалдарды қолдану нәтижесін көрнекі түрде кескіндеуді Эйлер-Венн диаграммасы арқылы беруге болады.
жиындарына теоретикалық-жиындық амалдарды қолдану нәтижесін көрнекі түрде кескіндеуді Эйлер-Венн диаграммасы арқылы беруге болады.
Ол үшін
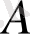 және
және
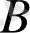 жиындары жазықтықта геометриялық фигура түрінде кескінделеді. Көпшілік жағдайда бұл мақсат үшін эллипс немесе шеңбер таңдалып алынады.
жиындары жазықтықта геометриялық фигура түрінде кескінделеді. Көпшілік жағдайда бұл мақсат үшін эллипс немесе шеңбер таңдалып алынады.
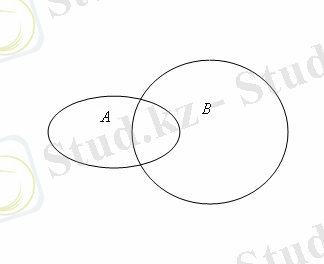
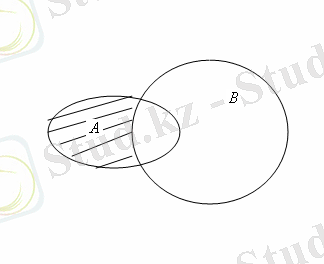
Жиындардың элементтері ретінде осы фигуралардың ішінде немесе шекараларында жататын жазықтықтың нүктелері алынады. Онда, егер
А
және
В
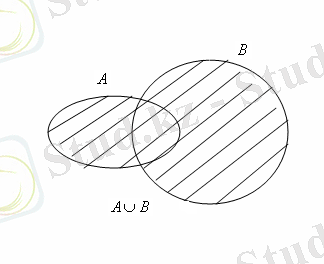
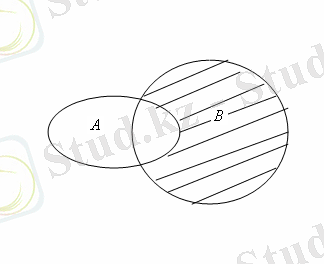
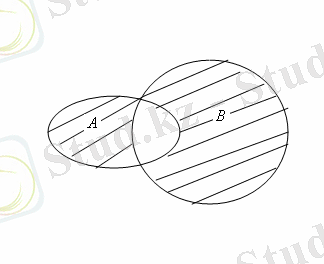
жиындары 2а - суретіндегідей кескінделсе, онда
 үшін кескіндер 2б, в, г - суреттеріндегідей кескінделеді.
үшін кескіндер 2б, в, г - суреттеріндегідей кескінделеді.
а) б)
в) г)
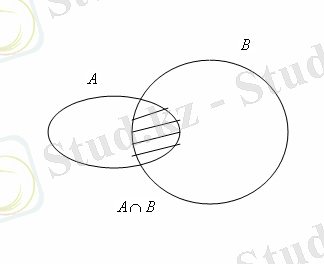
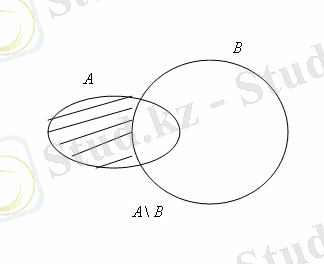
Cурет 2.
Көрнекі болу үшін диаграмманың сәйкес бөлігі штрихталып (боялып) көрсетілген.
Келесі жиындар үшін Эйлер-Венн диаграммаларын құрайық:
a)
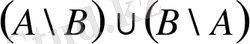 ;
;
б)
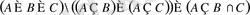 .
.
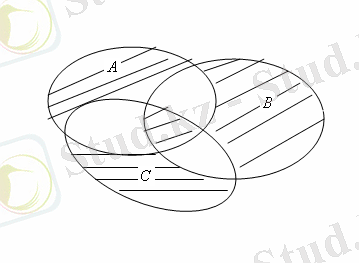
a) Диаграммаларды тізбектей құруды жүргізейік. (сурет 3а, б, в - қара)
Сурет 3.
б) Ақырғы нәтижені көрсетейік (4-суретке қара) .
Эйлер-Венн диаграммалар әдісі жиындардың теңбе-теңдігінде көрнекі түрде негіздеуге мүмкіндік береді. Ол үшін бірінші диаграммада теңбе-теңдіктің сол жақ бөлігіне сәйкес келетін жазықтықтың бөлігін штрихтың көмегімен бөліп аламыз. Осылай теңбе-теңдіктің оң жақ бөлігін анықтаймыз. Осыдан кейін штрихталған облыстарды салыстырамыз. Облыстардың сәйкес келуі беттесуі бізге берілген жиындардың шын мәніндегі теңдігі туралы қорытынды шығаруға мүмкіндік береді.
Сурет 4.
Мысалға, Эйлер-Венн диаграммасын пайдаланып,
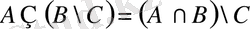
теңбе-теңдігін негіздейік.
Бұл жиынның сол жақ бөлігіне сәйкес келетін диаграмма 5а-суретінде кескінделген. Сол жағына сәйкес келетін диаграмма 5б-суретінде кескінделген.
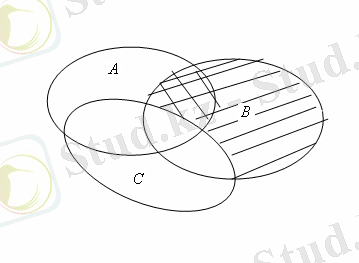
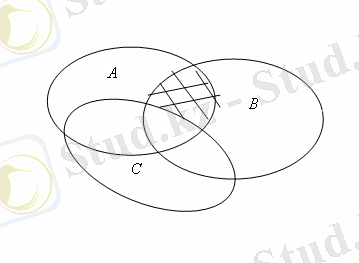
Сурет 5.
Бұл суреттердегі екі рет штрихталған жазықтықтың бөліктері бір-біріне тең. Шын мәнісінде бұл облыстар дәлелдеуді қажет ететін (дәлелденетін) теңбе-теңдіктің сол және оң жақ бөліктеріне сәйкес келеді.
§1. 5. Жиындардың декарттық көбейтіндісі
Жазықтықта тікбұрышты декарттық координат жүйесін енгізу осы жазықтықтағы әрбір
 нүктесімен
нүктесімен
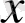 және
және
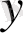 нақты сандарымен
нақты сандарымен
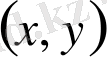 жұбын байланыстыруға мүмкіндік береді,
жұбын байланыстыруға мүмкіндік береді,
 және
және
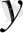 сандары
сандары
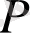 нүктесінің координаталары деп, және бұл жағдайда
нүктесінің координаталары деп, және бұл жағдайда
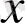 - бірінші координатасы (абцисса) деп, ал
- бірінші координатасы (абцисса) деп, ал
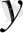 - екінші координатасы (ордината) деп саналады. Нүктенің координаталары болатын
- екінші координатасы (ордината) деп саналады. Нүктенің координаталары болатын
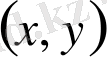 жұбы екі элементті
жұбы екі элементті
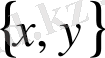 жиынынан мүлдем басқа (мағыналық түрде ажыратылады), себебі, жиындардың теңбе-теңдігі қатынасының анықтамасы бойынша:
жиынынан мүлдем басқа (мағыналық түрде ажыратылады), себебі, жиындардың теңбе-теңдігі қатынасының анықтамасы бойынша:
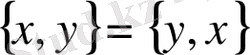 .
.
Ал,
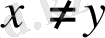 болғанда
болғанда
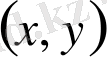 және
және
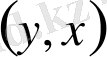 жұптары әртүрлі нүктелерді анықтайды.
жұптары әртүрлі нүктелерді анықтайды.
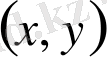 жұбының теоретикалық-жиындық мағынасы
жұбының теоретикалық-жиындық мағынасы
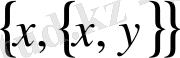 , ал
, ал
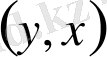 жұбының теоретикалық-жиындық мағынасы
жұбының теоретикалық-жиындық мағынасы
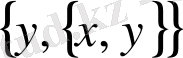 , сондықтан
, сондықтан
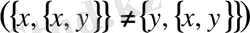 , яғни
, яғни
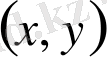 және
және
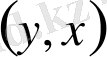 жұптары тең емес.
жұптары тең емес.
Сонымен,
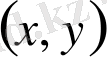 координаттық жұбы - бұл екі элементті жиын және оның элементтеріне қатысты қайсысы бірінші, қайсысы екінші деп есептеу туралы келісім қабылданған.
координаттық жұбы - бұл екі элементті жиын және оның элементтеріне қатысты қайсысы бірінші, қайсысы екінші деп есептеу туралы келісім қабылданған.
Бұл мағынадан алғанда координаталық жұп - реттелген екі элементті жиын немесе реттелген жұп.
Жалпы жағдайда
 және
және
 элементтері әр түрлі
элементтері әр түрлі
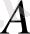 және
және
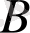 жиындарынан алынуы мүмкін.
жиындарынан алынуы мүмкін.
Бірақ бұрынғы анықтамадағы сияқты
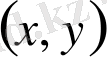 жұбын
жұбын
 реттелген деп санаймыз. Яғни, егер
реттелген деп санаймыз. Яғни, егер
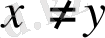 болса, онда
болса, онда
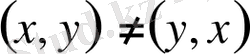 .
.
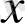 элементі
элементі
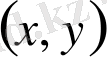 жұбының бірінші координатасы деп, ал
жұбының бірінші координатасы деп, ал
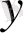 элементі оның екінші координатасы деп аталады. Жалпы алғанда жұптардың теңдігі туралы да айтуға болады.
элементі оның екінші координатасы деп аталады. Жалпы алғанда жұптардың теңдігі туралы да айтуға болады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz