Эллиптикалық теңдеулер: Лаплас және Пуассон теңдеулері, Дирихле мен Нейман шеттік есептері, Грин функциясы және сандық әдістер


Эллипстік типті теңдеулер
Лаплас теңдеуіне әкелетін есептер
Эллипстік типті теңдеулер станционарлық (тұрақты) процестерді, мысалы, денеде тұрақты температураның таралуы, өткізгіштің бетіндегі электр зарядтарының тепе-теңдік күйі, сұйықтың потенциалды ағысы т. с. с. процестерді сипаттайды. Осы сияқыт процестерді зерттеулер Лаплас теңдеуінің шешімін табу амалына әкеледі. Лаплас теңдеуі:
түрінде жазылады.
Теңдеудің сол жағына Лаплас операторын қолданып, былай жазуға болады:
Екі тәуелсіз айнымалылар үшін Лаплас теңдеуі
түрінде жазылады. Ал
түріндегі теңдеу Пуассон теңдеуі деп аталады.
Лаплас теңдеуін қанағаттандыратын функциялары гармоникалық функциялар деп аталады.
Біртекті денеде температураның тұрақталып таралуы
Біртекті Т денесі бетімен шектелген болсын дейік. Дененің әртүрлі нүктелеріндегі температура
теңдеуін қанағаттандырады. Егер температура уақыттан тәуелсіз болса, яғни онда дененің температурасы Лаплас теңдеуін қанағатандырады.
Осы теңдеуден дененің температурасы бір мәнді анықталуы үшін бетіндегі температураны білу керек. Сондықтан төмендегі теңдеу үшін
шеттік есеп былай қойылады:
1 Дирихле есебі (бірінші шеттік есеп)
Берілген Т облысында гармоникалық функция болатын, тұйық облысында үзіліссіз және облыстың шекарасында берілген үзіліссіз функциясына тең, яғни:
(2)
шартын қанағаттандыратын функциясын табу керек. Егер температураның таралуы жазықтықтағы С контуры мен D облысында қарастырылатын болса, онда:
теңдеуін қанағаттандыратын және С контурында функциясына тең функциясын табу керек.
2 Нейман есебі (екінші шеттік есеп)
Берілген Т облысында гармоникалық функция болатын, тұйық облысында үздіксіз дифференциалданатын, ал тегіс бетінен сыртқа қарай бағытталған нормаль бойынша алынған дифференциалданатын, ал тегіс бетінен сыртқа қарай бағытталған нормаль бойынша алынған туындысы осы беттің нүктелерінде берілген үздіксіз функциясына тең болатын, яғни:
(3)
шартын қанағаттандыратын функциясын табу керек.
Нейман есебі, екінші шеттік есеп - екінші ретті дербес туындысы бар дифференциалдық теңдеулер үшін қойылатын шеттік есептердің бірі. Нейман есебі қарапайым жағдайда (дербес жағдайда Лаплас теңдеуі үшін) белгілі бір облыста осы облыс шекарасында берілген нормаль туындының шешімін табуға қолданылады. Алғаш 1877 жылы К. Нейман (1832 - 1925) зерттеген.
Эллипстік типті теңдеудің классикалық түрінің мысалы Пуассон теңдеуі.
немесе болғанда Лаплас теңдеуі.
функциясының әр түрлі физикалық мағынасы бар, яғни стационарлық, уақытқа тәуелсіз, температураның бөлінуі идеалдық (үйкеліссіз және жылуөткізгіштіксіз) сұйықтықтың потенциал жылдамдықты (вихорьсіз) ағыны, электр және магнит өрісі кернеулігнің, тартылу өріс күш потенциалының бөлінуі, т. б.
Егер шекарадағы Г есептелінетін облыста, ізделінетін функция:
берілсе, онда Лаплас және Пуассон теңдеуінің бірінші шектік есебі Дирихле есебі деп аталады, яғни
Егер шекарада Г ізделінетін функцияның нормаль туындысы берілетін болса, онда Лаплас және Пуассон теңдеуінің екінші шектік есебі Нейман есебі деп аталады, яғни
Мұндағы, n - нормаль Г шекараға бағыты.
Ең тиімді әдіс шектік шарттың координаттық формасы болып табылады:
Мұндағы, − шекараға Г бағытталған бірлік нормаль векторына бағыттауыш косинустары, i және j - базис векторының орттары.
Пуассон (Лаплас) теңдеуінің үшінші шектік есебі мұндай түрде беріледі.
Есептің қойылуы
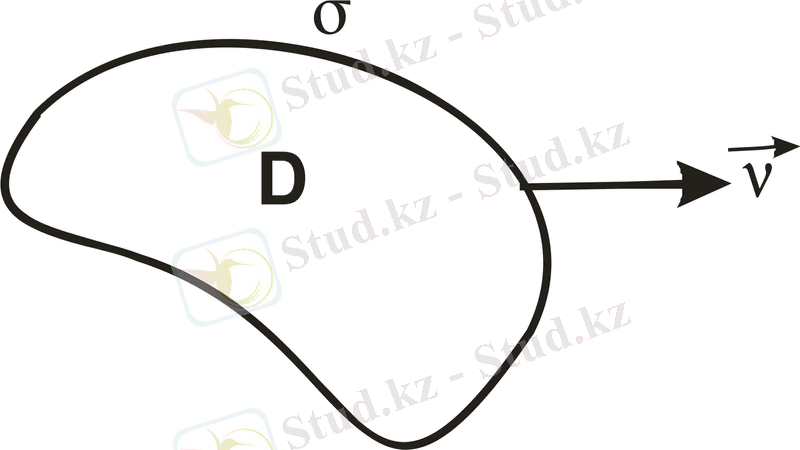
Лаплас теңдеуіне шекаралық есептердің қойылуларын көрсетейік (басқа эллиптикалық теңдеулерге осылайша, кейбір өзгерістер болуы мүмкін) .
А) Дирихленің ішкі есебі
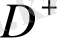 :
:
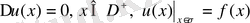 ;
;
б) Дирихленің сыртқы есебі
 :
:
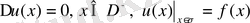 ;
;
шексіздікте регулярлы
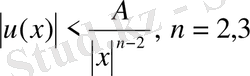 шешімді анықтау керек.
шешімді анықтау керек.
В) Нейманның ішкі есебі
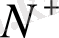 :
:
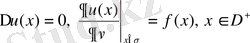 ;
;
г) Нейманның сыртқы есебі
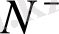 :
:
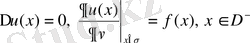 шексіздікте регуляр шешімін анықтау керек;
шексіздікте регуляр шешімін анықтау керек;
д) Жалпылама (үшінші текті) ішкі және сыртқы есептер:
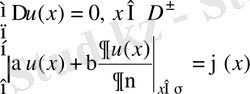 регуляр
регуляр
 функцияны анықтау керек.
функцияны анықтау керек.
Шеңбердегі Лаплас теңдеуі үшін Дирихле есебі
 ,
,
 деп ішкі және сыртқы аймақтарды белгілейік.
деп ішкі және сыртқы аймақтарды белгілейік.
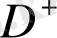 аймақ шекарасы
аймақ шекарасы
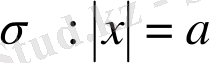 ,
,
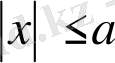 - шеңбер болсын. Осы аймақта
- шеңбер болсын. Осы аймақта
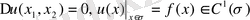 (7)
(7)
Дирихле есебін қарастырайық.
Есептің формальды шешімі
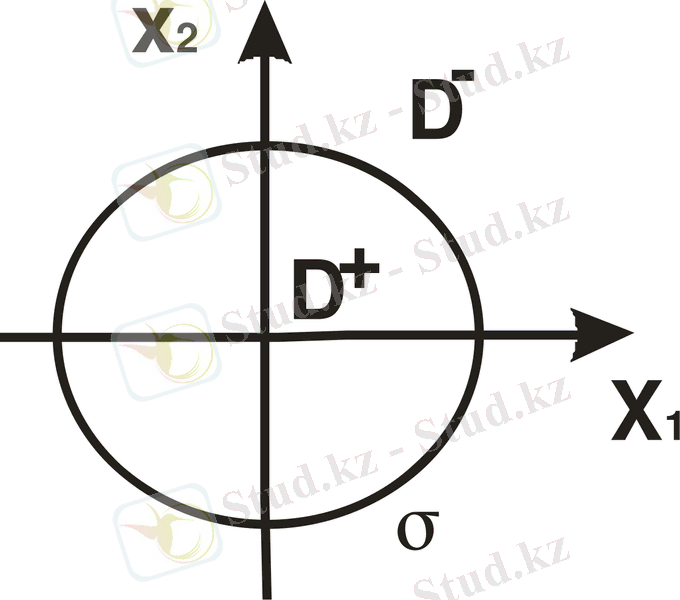
Есепті поляр координата жүйесінде
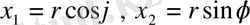 жазайық:
жазайық:
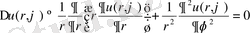 (8)
(8)
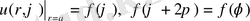 (9)
(9)
Бұл есептің периодты, шектелген шешімін (Фурье тәсілімен)
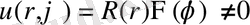 (10)
(10)
түрінде іздейміз.
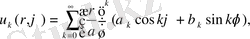 егер
егер
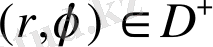 , (11)
, (11)
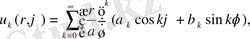 егер
егер
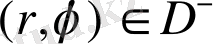 , (12)
, (12)
есептің формалдық шешімін аламыз.
Лаплас теңдеуіне қойылған Дирихле есебі үшін Грин функциясы
Грин функция анықтамасы және оның кейбір қасиеттері
Шенелген
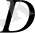 аймақ, ал
аймақ, ал
 оның шенелген жатық шекарасы болсын және
оның шенелген жатық шекарасы болсын және
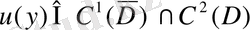 берілсін. Жоғарыда мүндай функция үшін төмендегі интегралдық өрнекті
берілсін. Жоғарыда мүндай функция үшін төмендегі интегралдық өрнекті
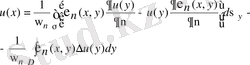 (13)
(13)
алғанбыз, мұндағы
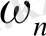 болса
болса
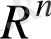 кеңістіктегі бірлік сфера бетінің ауданы, ал
кеңістіктегі бірлік сфера бетінің ауданы, ал
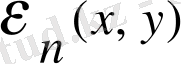 болса Лаплас теңдеуінің іргелі шешімі:
болса Лаплас теңдеуінің іргелі шешімі:
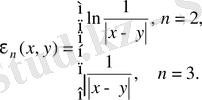
Егер мұндағы
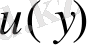 - гармониялық функция болса, онда (13) өрнектің оң жағындағы соңғы интеграл нөлге тең болып, нәтижеде пайда болған өрнекті гармониялық функцияның интегралдық кескіні деп атайды. Бұл кескін бойынша гармониялық функцияның
- гармониялық функция болса, онда (13) өрнектің оң жағындағы соңғы интеграл нөлге тең болып, нәтижеде пайда болған өрнекті гармониялық функцияның интегралдық кескіні деп атайды. Бұл кескін бойынша гармониялық функцияның
 аймақтағы өзінің және нормал вектор бойынша туындысы белгілі болса, онда интегралдық өрнек бойынша сол гармониялық функция барлық
аймақтағы өзінің және нормал вектор бойынша туындысы белгілі болса, онда интегралдық өрнек бойынша сол гармониялық функция барлық
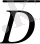 тұйық аймақта анықталады.
тұйық аймақта анықталады.
Бірақ гармониялық функция үшін қойылған Дирихле есебінде
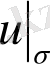 белгілі де, ал
белгілі де, ал
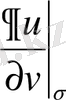 белгісіз; Нейман есебінде керісінше.
белгісіз; Нейман есебінде керісінше.
Сол шенелген
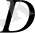 аймаққа
аймаққа
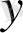 айнымалы бойынша гармониялық функция болатын
айнымалы бойынша гармониялық функция болатын
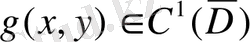 функция енгізейік.
функция енгізейік.
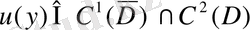 және
және
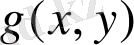 функциялар үшін Гриннің екінші формуласын
функциялар үшін Гриннің екінші формуласын
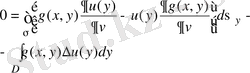 (14)
(14)
жазайық; оны
 шамаға көбейтіп (13) - мен, сәйкес мүшелерін қосайық, нәтижеде
шамаға көбейтіп (13) - мен, сәйкес мүшелерін қосайық, нәтижеде
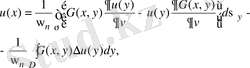 (15)
(15)
мұндағы
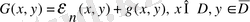 . (16)
. (16)
Егер еркін алынған
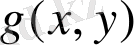 гармониялық функцияны
гармониялық функцияны
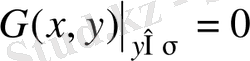 болатындай таңдап алсақ, онда соңғы теңдеудегі
болатындай таңдап алсақ, онда соңғы теңдеудегі
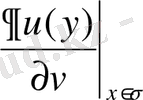 бар интеграл нөлге айналады. Бұл жағдайда жоғарыдағы Дирихле есебіндегі белгісіз
бар интеграл нөлге айналады. Бұл жағдайда жоғарыдағы Дирихле есебіндегі белгісіз
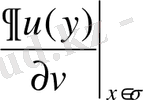 шама болмайды да есеп оңай шешіледі.
шама болмайды да есеп оңай шешіледі.
Анықтама.
Егер (16) өрнектеп алынған
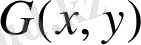 функция
функция
1
0
Лаплас теңдеуінің іргелі шешімімен
 аргументі бойынша
аргументі бойынша
 аймақта гармониялық
аймақта гармониялық
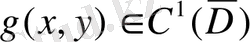 функция қосындысына тең, яғни (16) орынды болса;
функция қосындысына тең, яғни (16) орынды болса;
2
0
Ол
 бетте
бетте
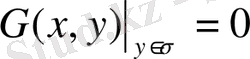 шартты қанағаттандырса, оны
Грин функциясы
деп атайды.
шартты қанағаттандырса, оны
Грин функциясы
деп атайды.
Бұл функцияның кейбір айқын қасиеттерін қарастырайық
1-қасиеті.
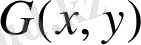 функция
функция
 аргументі бойынша шенелген
аргументі бойынша шенелген
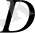 аймақта
аймақта
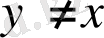 жағдайда гармониялық және үзіліссіз функция болады.
жағдайда гармониялық және үзіліссіз функция болады.
2-қасиеті. Грин функциясын құру үшін мына Дирихле есебін
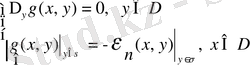 (17)
(17)
шешу керек.
3-қасиеті. Егер Грин функциясы бар болса, ол жалғыз.
4-қасиеті.
Грин функциясы
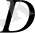 аймақта теріс емес.
аймақта теріс емес.
1-ескерту.
Дирихле есептерінің шешімдерін құруда есептің шешімінің
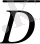 аймақта үзіліссіз дифференциалданатын пайдаландық.
аймақта үзіліссіз дифференциалданатын пайдаландық.
Егер
 бет Ляпунов типіндегі болса, онда жоғарыдағы шешім
бет Ляпунов типіндегі болса, онда жоғарыдағы шешім
 үшін орынды.
үшін орынды.
5-қасиеті. Грин функциясы аргументтерін салыстырғанда симметриялы функция, яғни
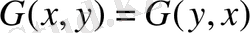
және Грин функциясы аргументтерінің біреуін тұрақталса екінші координатасы бойынша Лаплас теңдеуін қанағаттандырады; яғни егер
 тұрақтандырылса, онда
тұрақтандырылса, онда
 үшін
үшін
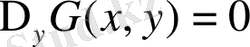 және керісінше
және керісінше
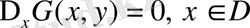 .
.
Грин функциясын пайдаланып Дирихле есебін шешу
1.
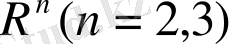 кеңістіктегі шардағы (шеңбердегі) Дирихле есебі
кеңістіктегі шардағы (шеңбердегі) Дирихле есебі
Шенелген сферамен
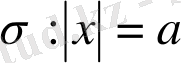 қоршаланған
қоршаланған
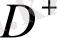 шарда Лаплас теңдеуіне
шарда Лаплас теңдеуіне
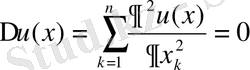 (18)
(18)
қойылған Дирихле есебін
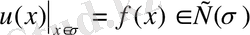 (19)
(19)
шекаралық шартпен шешу есебіне Грин функциясын пайдаланайық.
Егер бұл есептің шешімі бар болса, онда ол төмендегі формула арқылы:
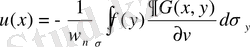 (20)
(20)
өрнектеледі.
Ал, өткен параграфта Грин функциясы (17) формуламен анықталынған. (18) шешімде
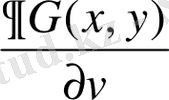 туындыны анықтау керек.
туындыны анықтау керек.
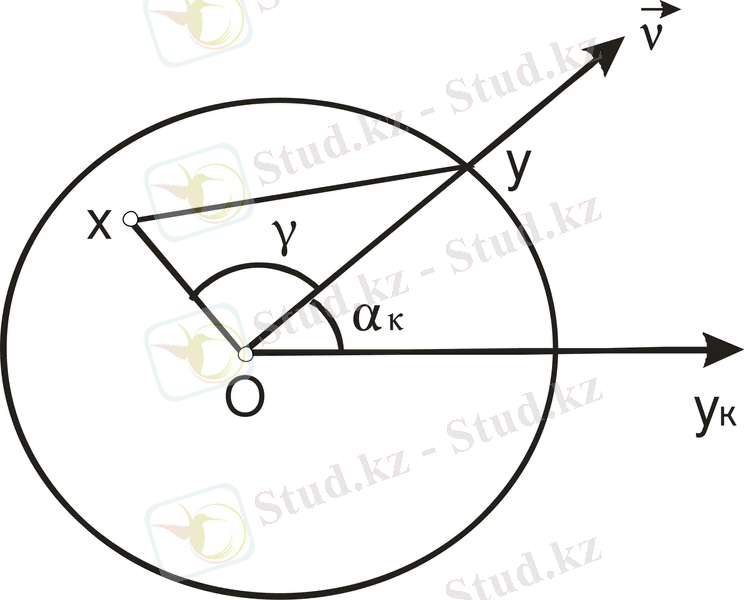
Сурет бойынша: сыртқы бірлік
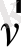 нормаль бағыты шардың
нормаль бағыты шардың
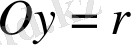 радиусымен бағыттас енгізейік те:
радиусымен бағыттас енгізейік те:
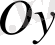 радиус пен
радиус пен
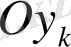 координата өсі арасындағы бұрыш
координата өсі арасындағы бұрыш
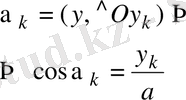 .
.
 және
және
 скаляр тұрақтылар
скаляр тұрақтылар
Содан
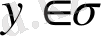 бойынша туындыны
бойынша туындыны
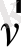 бағыты бойынша есептейік:
бағыты бойынша есептейік:
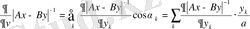 ,
,
бірақ
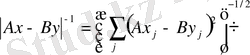 болғандықтан
болғандықтан
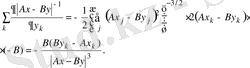 (21)
(21)
Егер (21) өрнекке
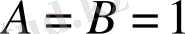 деп алсақ, онда
деп алсақ, онда
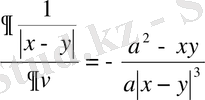 ; (22)
; (22)
ал оған
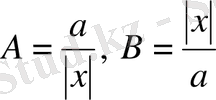 деп қабылдасақ, онда
деп қабылдасақ, онда
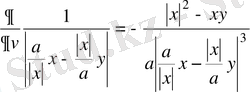 .
.
Грин функциясының қасиеті бойынша
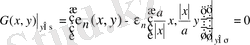 ,
,
ал
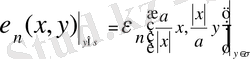 болғандықтан
болғандықтан
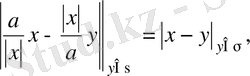
туынды
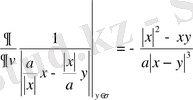 . (23)
. (23)
Міне осы (22), (23) туындыларды қосып Грин функциясының
 бағыт бойынша туындысын
бағыт бойынша туындысын
 үшін:
үшін:
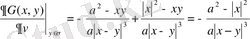 ,
,
ал
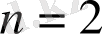 үшін
үшін
 .
.
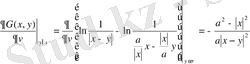
Бұл екі туындаларды (19) формулаға қойып Лаплас теңдеуіне қойылған Дирихле есебінің
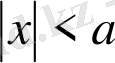 шар
шар
 (
(
 шеңбер) үшін
шеңбер) үшін
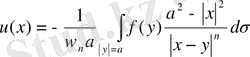 ,
,
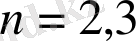 (24)
(24)
Пуассон интегралы деп аталатын шешімін анықтаймыз.
Егер суретті пайдалансақ, яғни
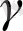 деп
деп
 ,
,
 өстер арасындағы бұрышты белгілесек, онда
өстер арасындағы бұрышты белгілесек, онда
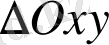 - тен
- тен
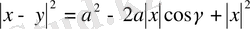 .
.
 үшін поляр координата жүйесін
үшін поляр координата жүйесін
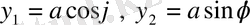 арқылы енгізіп
арқылы енгізіп
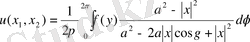 , (24’)
, (24’)
ал
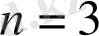 үшін (сфералық координата жүйесін енгізіп)
үшін (сфералық координата жүйесін енгізіп)
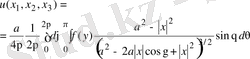 (24’’)
(24’’)
айқын түрдегі шешімдерді аламыз.
Дирихленің сыртқы есебі:
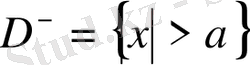 аймақта
аймақта
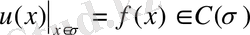 шекаралық шартты қанағаттандыратын
шекаралық шартты қанағаттандыратын
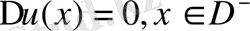 теңдеудің шексіздікте регуляр шешімін анықтау керек.
теңдеудің шексіздікте регуляр шешімін анықтау керек.
Бұл есептің ішкі есептен талдауының бір ғана айырмасы, ол
 бетке тұрғызылған
бетке тұрғызылған
 нормаль
нормаль
 аймақ үшін
аймақ үшін
 сфераның центріне бағытталған болып, Грин функциясының
сфераның центріне бағытталған болып, Грин функциясының
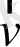 бойынша туындысы
бойынша туындысы
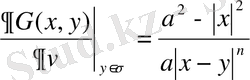 түрінде өрнектеліп, есеп шешімі
түрінде өрнектеліп, есеп шешімі
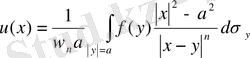 (25)
(25)
болады. Бұл шешімнің гармониялылығы және шекара шартын қанағаттандыру ішкі есептегідей, дәлелденеді, егер инверсиялық түрлендіруді пайдаланса.
Шешімнің
 -дегі шексіздікте регуляр екенін көрсетейік.
-дегі шексіздікте регуляр екенін көрсетейік.
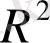 кеңістіктегі шешімнің регулярлығы деп ол шешімнің шексіздікте шенелгендігі.
кеңістіктегі шешімнің регулярлығы деп ол шешімнің шексіздікте шенелгендігі.
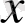 нүктені қашықтық
нүктені қашықтық
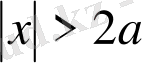 болатындай етіп таңдайық, онда
болатындай етіп таңдайық, онда
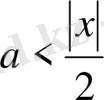 болады; ал
болады; ал
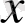 нүктеден
нүктеден
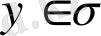 ара қашықтығы үшін, бұл жағдайда,
ара қашықтығы үшін, бұл жағдайда,
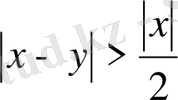 орынды. Демек
орынды. Демек
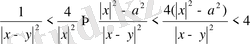 , олай болса,
, олай болса,
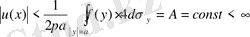 .
.
Дәл осылайша
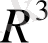 - тегі шешімнің регулярлығы
- тегі шешімнің регулярлығы
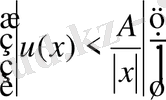 дәлелденеді.
дәлелденеді.
Ескерту.
(71) Пуассон формуласы
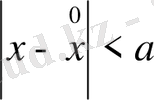 шар үшін
шар үшін
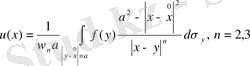 (26)
(26)
түрінде жазылады.
Жарты кеңістік үшін Дирихле есебі
Жоғарыда алынған жарты кеңістік үшін Грин функциясын мына жарты кеңістік үшін Лаплас теңдеуіне қойылған Дирихле есебін:
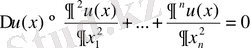 , (27)
, (27)
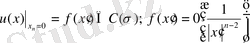 (28)
(28)
шешуге қолданайық.
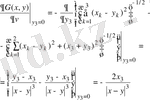
Дәл осылай
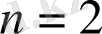 үшін
үшін
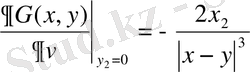 (30)
(30)
Бұл шешімдердің есепті қанағаттандыратыны және регулярлылығы жоғарыдағыдай дәлелденеді.
Мысал. Теңдеуді шешу:
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz