Мектеп математика курсында функция ұғымын қалыптастыру және функциялық мазмұнды есептерді оқыту әдістемесі


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 51 бет
Таңдаулыға:
ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
ҚАЗАҚ МЕМЛЕКЕТТІК ҚЫЗДАР ПЕДАГОГИКА ИНСТИТУТЫ
Физика-математика факультеті
Математика кафедрасы
ДИПЛОМДЫҚ ЖҰМЫС
Мектеп математика курсындағы функциялық мазмұнды есептер
Орындаған: 4 курс күндізгі оқу бөлімінің студенті Мырзабекова С. С.
Ғылыми жетекшісі: п. ғ. к., доцент Қасқатаева Б. Р. «» 2007ж.
«Қорғауға жіберілді»
Кафедра шешімі, хаттама №
Кафедра меңгерушісі: ф. -м. ғ. к., доцент Искакова А. Қ.
«» 2007ж.
Алматы 2007ж.
МАЗМҰНЫ
КІРІСПЕ . . . 3
I - ТАРАУ. МАТЕМАТИКАНЫ ОҚЫТУ БАРЫСЫНДА ФУНКЦИЯ ҰҒЫМЫН ҚАЛЫПТАСТЫРУ
І. 1. Сәйкестік ұғымын енгізу әдістемесі . . . 4-9
1. Жиындар арасындағы сәйкестік . . . 4-7
2. Кері сәйкестік . . . 7- 8
3. Өзара бірмәнді сәйкестік . . . 8-9
І. 2. Функция ұғымын енгізу әдістемесі . . . 9-21
І. 3. Тапсырмалар жүйесі . . . 21-27
ІІ - ТАРАУ. МЕКТЕП МАТЕМАТИКА КУРСЫНДАҒЫ ФУНКЦИЯЛЫҚ МАЗМҰНДЫ ЕСЕПТЕР
ІІ. 1. Функционалдық мазмұнды есептерді шығаруға үйрететін дайындық (пропедевтикалық) жұмыс . . . 28-31
ІІ. 2. Сызықты функцияға келтіретін мәселе есептер . . . 31-33
ІІ. 3. Квадраттық функцияға келтіретін мәселе есептер . . . 33-35
ІІ. 4. Әртүрлі функциялық мазмұнды есептер . . . 35-45
ҚОРЫТЫНДЫ . . . 46
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР . . . 47
КІРІСПЕ
Менің «Мектеп математика курсындағы функциялық мазмұнды есептер» тақырыбына жазылған дипломдық жұмысым екі тараудан тұрады.
Кіріспеде жұмыстың көкейкестілігін және мақсатын, зерттеудің ғылыми болжамын келтірдім.
Бірінші тарауда математиканы оқыту барысында функция ұғымын қалыптастыру әдістемесін қарастырдық.
“Жиындар арасындағы сәйкестік”, “Сәйкестік және қатынас” геометрия курсында, “Фигураларды бейнелеу” тақырыптары алгебра курсына дайындық болады. Сондықтан, біз алдымен жиындар арасындағы сәйкестікке тоқталдық.
Екінші тарауында мектеп математика курсындағы функционалдық мазмұнды есептер қарастырылды.
Функция ұғымы математиканың фундаменталды ұғымдарының бірі. Мектеп математика курсында «Функция» тақырыбын оқытуда функциялық мазмұнды есептер үлкен рөл атқарады. Функция ұғымын енгізу үшін функциялық мазмұнды есептер шығарылады. Функциялық мазмұнды есептерді шешу оқушылардың функционалдық байланыс идеясын терең түсінулеріне және есептеу мәдениеттері мен ойлау қабілеттерін дамытуда алатын орны аса зор.
Функциялық мазмұнды мәселе есептер «Функция» тақырыбын оқытудың соңғы сатысында бекіту мақсатында да қолданылып отырады. Функциялық мазмұнды есептерді шығару оқушылардың «функция» ұғымын жете түсінуіне көмектеседі, оқушылардың ойлау, бақылау, салыстыру қабілеттерін дамытады және олардың нақты объекттер мен құбылыстарды модельдеу білігі мен дағдыларын қалыптастырады. Сондықтан «Функциялық мазмұнды есептер» тақырыбына жазылған дипломдық жұмыс көкейкесті деп ойлаймын.
Зерттеу обьектісі - жалпы білім беретін орта мектепте математиканы оқыту үрдісі.
Зерттеудің пәні - математиканы оқыту жағдайында оқушылардың функционалдық білімдерін қалыптастыру және дамыту мақсатында математика сабағында функциялық мазмұнды есептерді шешуді зерттеу.
Зерттеудің мақсаты - орта мектепте математика сабағында функциялық мазмұнды есептерді шешуге дағдыландыру.
Зерттеудің ғылыми болжамы - егер оқушылар математика сабағында функциялық мазмұнды есептерді шешуге дағдыланса, онда ол оқушылардың функционалдық білім сапасын көтеруге және математикалық қабілеттерін арттыруға септеседі.
Зерттеудің міндеттері - математиканы оқытқанда функциялық мазмұнды есептерді қолдану мүмкіндіктерін анықтау.
Зерттеудің практикалық маңызы: «Мектеп математика курсындағы функциялық мазмұнды есептер» тақырыбына жазылған дипломдық жұмысты мектеп мұғалімдері қолдануларына болады деп ойлаймын.
I ТАРАУ. МАТЕМАТИКАНЫ ОҚЫТУ БАРЫСЫНДА ФУНКЦИЯ ҰҒЫМЫН ҚАЛЫПТАСТЫРУ
І. 1. Сәйкестік ұғымын енгізу әдістемесі
Функция ұғымы математиканың фундаментальды ұғымдарының бірі. Ол мектеп математика курсында 7-11 сыныптарында оқылады. Функция ұғымына дайындық бастауыш мектептен басталады. Функция ұғымы сәйкестік және қатынас ұғымдарының негізінде пайда болды. Сәйкестік және қатынас бастауыш мектептің бірінші сыныбынан бастап қолданылады. Мысалы: «артық», «кем», «ұзын», «қысқа», «артық немесе тең», «биік немесе аласа», «кем немесе тең» қатыстары қарастырылып, сандардың және кесінділердің жиынында реттілік орнатылады.
Сәйкестік және қатынас ұғымдары жиын теориясымен тығыз байланысты. Мысалы,
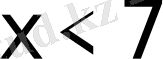 теңсіздігінің шешімі:
теңсіздігінің шешімі:
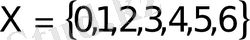 . Жиын теориясының ұғымдары мен символдары “теңдеулер және теңсіздіктер” тақырыбын өткенде қолданылады. Атап айтқанда:
. Жиын теориясының ұғымдары мен символдары “теңдеулер және теңсіздіктер” тақырыбын өткенде қолданылады. Атап айтқанда:
- “екі белгісізді теңдеудің графигі координаттары берілген теңдеуді қанағаттандыратын нүктелер жиыны”.
- Теңдеулер жүйесін шешу - оның шешімдер жиынын табу.
- Теңдеулер жүйесінің шешімдер жиыны - оның барлық теңдеулерінің шешімдер жиындарының қиылысуы.
Алгебра курсында функцияның анықталу облысы мен өзгеру облысы, сәйкесінше, “х-тәуелсіз айнымалылар қабылдайтын мәндерінің жиыны”, “у-тәуелді айнымалылар қабылдайтын мәндерінің жиыны”, - деп “жиын” ұғымы арқылы анықталады. “Декраттық
ХхУ
көбейтіндісінің кез келген ішкі
 жиыны
Х
пен
У
тең алынған элементтердің бинарлық қатынасы” деп атайды.
жиыны
Х
пен
У
тең алынған элементтердің бинарлық қатынасы” деп атайды.
“Жиындар арасындағы сәйкестік”, “Сәйкестік және қатынас” геометрия курсында, “Фигураларды бейнелеу” тақырыптары алгебра курсына дайындық болады. Сондықтан, біз алдымен жиындар арасындағы сәйкестікке тоқталайық.
1. Жиындар арасындағы сәйкестік
Екі жиынның элементтерінің арасындағы қандай да бір байланыс жиі қарастырылады. Осындай байланысты сәйкестік деп атайды. Мысалы, кесінділердің ұзындығын өлшегенде кесінді мен нақты сандардың арасында, жазықтықтағы нүктелер мен нақты сандар қосының арасында сәйкестік бар.
Анықтама: Х және У жиындарының элементтерінің арасындағы сәйкестік деп олардың декарттық көбейтіндісінің ішкі жиыны болатын қостардың жиынын айтады.
Ақырлы жиындардың арасындағы сәйкестікті график арқылы көрнекті түрде бейнелеуге болады.
Мысалы, Х={3; 5; 7; 9}, У={4; 6} жиындарының арасындағы «артық» (үлкен) деген сәйкестікті график арқылы көрсетейік. Ол үшін берілген жиындардың элементтерін нүктелер арқылы кескіндеп, X жиынының элементін кескіндейтін нүктеден У жиынының элементін кескіндейтін нүктені стрелкамен қосамыз, сонда элементтердің арасында "артық" сәйкестігі орындалуы керек. 5>4 болғандықтан стрелка 5-тен 4-ке қарай; 7>4, 7>6 болғандықтан 7-ден 4-ке, 7-ден 6-ға қарай т. с. с. бағытталуы тиіс (1-сызба) .
Сонда шыққан сызба X және У жиындарының элементтерінің арасындағы «артық» деген сәйкестіктің графы болады.
X, У сандық жиындардың арасындағы сәйкестікті координаттық жазықтықтағы график арқылы да көрсетуге болады. Ол үшін қандай да бір R сәйкестікте болатын сандардың қосын координаттық жазықтықтағы нүктелер арқылы бейнелейді. Сонда алынған фигура R сәйкестігінің графигі болады. Жоғарыда қарастырылған мысалдағы «артық» сәйкестігінің графигін сызайық.
Берілген сәйкестікте болатын сандардың қосын жазайық: (5; 4), (7; 4), (7; 6), (9; 4), (9; 6) . X жиынның элементтерін Ох осінің бойынан, У жиынының элементтерін Оу осінің бойынан алып, көрсетілген сандардың қосына сәйкес келетін нүктелерді координаттық жазықтықта белгілесек, X және У жиындарының элементтерінің арасындағы «артық» сәйкестігінің графигін аламыз (2-сызба) .
Х У
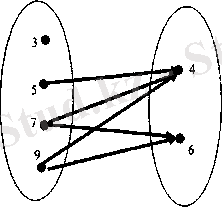
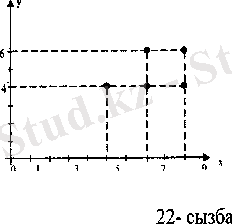
1-сызба
Енді «артық» сәйкестігін Х=R және У={4; 6} жиндарында қарастырып, оның графигін салайық.
Бұл жағдайда X жиынының элементтері бүкіл Ох осінің бойындағы нүктелерден, ал У жиыны екі элементтен тұрады.
X және У жиындарының элементтері үшін "артық" сәйкестігі берілгендіктен, X жиынындағы 4-тен артық болатын сандарды анықтаймыз. 4-тен артық барлық сандар Ох осінің бойында 4 санына сәйкес келетін нүктенің оң жағында орналасқан. Демек, абсциссасы (4; ∞) аралығынан алынған, ал ординатасы 4-ке тең болатын СД сәулесі 4-тен артық сандардың графигін береді.
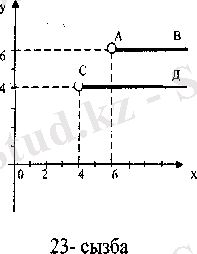
СД сәулесінің басы (4; 4) нүктесі графиікке енбейді, себебі 4>4 сәйкестігі жалған. Дәл осылайша, абсциссасы (6; ∞) аралығынан, ординатасы 6-ға тең болатын АВ сәулесі 6-дан үлкен сандардың графигі болады (3-сызба) . Сонымен, Х=R, Y={4; 6} жиындарының арасындағы «артық» сәйкестігінің графигі А және С нүктелері енбейтін АВ және СД сәулелері болды.
Әртүрлі жиындар арасындағы бір ғана «артық» сәйкестігінің графиктерінің әртүрлі екенін көрдік.
Енді накты сандар жиынында х=R, у=R болғанда (x>у) «артық» сәйкестігінің графигін салайық.
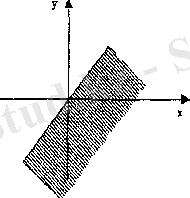
4-сызба
Абсциссасы мен ординатасы тең болатын сандар I және III координаталық ширектерден өтетін биссектрисаның бойында жатады. Абсциссасы ординатасынан үлкен болатын нүктелер осы биссектрисаның төменгі жағына орналасады (4-сызба) .
Сонымен, х=R, у=R болғанда «артық» сәйкестігінің графигі жазықтықтың бөлігі болды, немесе х=у түзуімен анықталған төменгі (оң жақтағы) жарты жазықтық болады.
Жиындар арасындағы сәйкестік үғымы математикадағы негізгі ұғымдардың қатарына жатады. Олай болатын себебі, бұл (4-сызба) ұғым математикадағы функция және бейнелеу сияқты аса маңызды үғымдарды анықтаудың негізі болып табылады. Сонымен қатар кез келген ғылымда объектілердің өздері ғана емес, олардың арасындағы байланыстар да зерттеледі. Мысалы, географияда қалалар жиыны X және елдер жиыны У арасындағы "X қаласы У еліне қарайды деген" сәйкестік қарастырылады. Физикада: "х денесінің массасы у-ке тең", химияда: "х затының таңбасы у болады", математикада: "х фигурасының ауданы у-ке тең" деген т. с. с. сәйкестіктер қарастырылады.
2. Кері сәйкестік
Х={3; 5; 7}, У={4; 6} жиындарының элементтерінің арасында R «артық» сәйкестігі берілсін. Сонда R={(5; 4), (7; 4), (7; 6) } және оның графы 5-сызбадағыдай болады.
Осы графтағы стрелкалардың бағытын кері өзгертейік. Сонда У және X жиындарының элементтерінің арасындағы "кем" сөйкестігінің графы алынады (6-сызба) .
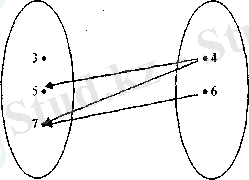
Х У Х У
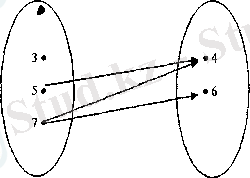
6-сызба
5- сызба
Графы 6-сызбада кескінделген сәйкестік берілген R сәйкестігіне кері сәйкестік деп атальп, R -1 арқылы белгіленеді.
А н ы қ т а м а: X және У жиындарының арасындағы сәйкестік R болса, онда У және X жиындарының арасындағы уR -1 х болатындай R -1 сәйкестігі хRу болғанда және тек сонда ғана R сәйкестігіне кері сәйкестік деп аталады.
R және R -1 сәйкестері өзара кері сәйкестіктер деп аталады. Өзара кері сәйкестіктердің графиктерінің қандай ерекшеліктері болатынын анықтайық.
R={(5; 4), (7; 4), (7; 6) } сәйкестігінін графигін салайық (7-сызба) . R -1 = {(4; 5), (4; 7), (6; 7) } сәйкестігінің графигін салғанда қостың бірінші компонентін У жиынынан екінші компонентін X жиынынан алу керек. R -1 сәйкестігінің графигі R сәйкестігінің графигімен беттесетінін көреміз.
Бұл графиктерді ажырату өте қолайсыз. Сондықтан, R -1 сәйкестігіндегі қостардың бірінші компонентін абсцисса осінен, екінші компонентін ордината осінен алу келісілген. Мысалы, (5; 4) ∈R онда (4; 5) ∈ R -1 .
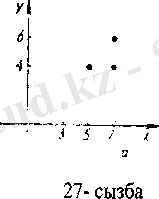
Координаталары (5; 4) және (4, 5), жалпы жағдайда (х; у) және (у; х) болатын нүктелер I және III координаттық бұрыштардың биссектрисасына қарағанда симметриялы болады. Сонымен, R сәйкестігіне кері R -1 сәйкестігінің графигі R сәйкестігінің графигінің нүктелеріне I және III координаттық бұрыштар арқылы өтетін биссектрисаға қарағанда симметриялы нүктелерден тұрады. Сондықтан R -1 ={(4; 5), (4; 7), (6; 7) } болатын сәйкестіктің графигі 8-сызбада бояп көрсетілген нүктелер жиынынан тұрады.
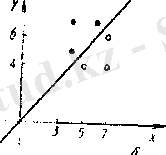
Натурал сандар жиынындағы R "х кем у-тен" сәйкестігі болса, оған кері R -1 сәйкестігі "х артық у-тен" болады. Кесінділер арасындағы "х кесіндісі у-тен ұзын" сәйкестігіне "х кесіндісі у-тен қысқа" деген сәйкестік кері болады.
Бастауыш мектептің математика курсында өзара кері сәйкестікке көп көңіл бөлінеді. Оқушылар 5>3 болғандықтан 3<5 екенін, егер АВ кесіндісі СД
8- сызба кесіндісінен ұзын болса, онда СД кесіндісі АВ кесіндісінен қысқа болатынын терең түсінуі керек.
3. Өзара бірмәнді сәйкестік
X және У жиындарының элементтерінің арасындағы барлық мүмкін сәйкестіктердің ішінен X жиынындағы әрбір элементке У жиынынан жалғыз элемент және керісінше, У жиынының әрбір элементіне X жиынының жалғыз элементі сәйкес келетін сәйкестікті қарастырамыз. Мұндай сәйкестікті өзара бірмәнді сәйкестік деп атайды.
Осындай сәйкестіктерге мысалдар қарастырайық:
1. А={а; b; с; d}, В={1; 2; 3, 4} болсын. Бұл жиындардың элементтерінің арасындағы сәйкестік былайша көрсетілген (9-сызба) .
А жиынындағы әрбір элементке В жиынынан жалғыз элемент сәйкес келеді. Сонымен қатар керісінше, В жиынындағы әрбір элементке А жиынынан жалғыз элемент сәйкес келеді. Сондықтан А және В жиындарының арасындағы сәйкестік өзара бірмәнді болады (9- сызба) .
Х У
9-сызба
2. X координаттық түзудің бойындағы нүктелер жиыны, У = R болсын.
Координаттық түзуді енгізуге байланысты түзудегі әрбір нүктеге бір нақты сан (сол нүктенің координатасы) сәйкес келеді және кез-келген нақты санға түзудің бойынан бір нүкте сәйкес келеді. Сонда бұл сәйкестік те өзара бірмәнді болады.
3. Х -координаттық жазықтықтағы нүктелер жиыны, ал У -нақты сандардың қостарының жиыны болсын.
Егер жазықтықтағы әрбір нүктеге нақты сандардың жалғыз қосы (нүктенің координаталары) сәйкес келсе және нақты сандардың әрбір қосына жазықтықтан бір нүкте сәйкес келсе, онда жазықтыктағы нүктелер жиыны мен нақты сандардың қостарының жиынының арасында өзара бірмәнді сәйкестік орнатылады.
Математиканың бастауыш мектептегі курсында өзара бірмәнді сәйкестік ұғымы айқын түрде қолданылмайды: оған санау және сандарды салыстыру процесі негізделген.
Мысалы, 3=3 теңдігін түсіндіру үшін үш қызыл, үш көк шаршыны алып, әрбір қызыл шаршыға бір көк шаршыны сәйкес қояды (шаршыны бір-біріне беттестіріп қояды, оларды кесінділермен қосады т. с. с. ), яғни қызыл және көк түсті шаршылар жиындары арасында өзара бір мәнді сәйкестік орнатылады. 3<4 теңсіздігін көрсету үшін үш элементті жиын мен төрт элементті жиынының үш элементті ішкі жиындарының арасында өзара бірмәнді сәйкестік орнатылады.
I. 2. Функция ұғымын енгізу әдістемесі
Нақты өмірдегі процестер мен құбылыстар бір-бірімен байланыста болады. Мысалы, бір кесек темірді қыздырғанда оның ұзындығы өзгерсе, дене козғалысының жылдамдығы уақытқа тәуелді т. с. с. Екі айнымалы шамалардың арасындағы байланысты қамтитын математикалық ұғым - функция ұғымы. Функционалдық байланыс былай анықталады: “Егер х-тың қабылдайтын әрбір мәніне у-тің бір ғана мәні сәйкес келсе, онда
у, х
-ке тәуелді
функция
деп,
у= f(х)
түрінде жазылады”. Мұндағы
f
белгісі (символы)
х
аргументі мен
у
функция мәндерінің арасындағы сәйкестік заңдылығын көрсетеді. Функцияларды
 , F,
, F,
 , т. б. әріптерімен белгілейді; х аргументінің қабылдайтын мәндер жиынын функцияның
анықталу облысы
деп,
Х
не
Д
әріптерімен белгілейді;
у
функциясының мәндерінің жиынын функцияның
өзгеру облысы
деп
У
не
Е
әріптерімен белгілейді.
, т. б. әріптерімен белгілейді; х аргументінің қабылдайтын мәндер жиынын функцияның
анықталу облысы
деп,
Х
не
Д
әріптерімен белгілейді;
у
функциясының мәндерінің жиынын функцияның
өзгеру облысы
деп
У
не
Е
әріптерімен белгілейді.
Мысалдар қарастырайық:
1- м ы с а л : у=х 2 -7.
Шешуі: х-аргументтің мәні қандай болса да оны квадраттап және оның нәтижесінен 7-ні азайтуға болады. Олай болса бұл мысалда х -тің қабылдайтын мәндері - кезкелген нақты сан. Функция - 7-ден кіші емес мәндер қабылдайды, яғни у ≥-7.
2 - м ы с а л :
у=
 .
.
Шешуі: Функцияның анықталу облысын мынандай теңсіздік түрінде жазуға болады. -1≤ х ≤ 1, себебі х - тің бұл теңсіздікті қанағаттандырмайтын басқа мәндерінде жорaмал сандар алар едік.
Функцияның өзгеру облысы 0 ≤ у ≤ 1 теңсіздігімен анықталады. Сонымен Д = [-1; 1], Е = [0; 1] .
3 - м ы с а л : у=sіnx.
Шешуі: х-кезкелген нақты мән қабылдайды : яғни, Д = (-∞; +∞), -1≤ у ≤1, Е =[-1, 1] .
Функцияның берілу тәсілдері:
1) аналитикалық (формула арқылы) ;
2) графиктік (өзін өзі есепке алатын тетіктерде қолданылады) .
3) кесте (таблица) арқылы беріледі (Брадис таблицасы мысал бола алады) .
Функция туралы жалпы мәліметтермен танысуда функцияның фор-муламен берілуін пайдаланайық.
4 - м ы с а л : Жаяу адамның 70 м/мин жылдамдықпен жүрген жолы қозғалу уақытына тәуелді болады.
Жаяу адамның қозғалу уақытын (минут есебімен) t әрпімен, жүрген жолын (метр есебімен) s әрпімен белгілеп, t айнымалысының әрбір мәні үшін s айнымалысының сәйкес мәнін табайық:
егер t =1, 5 болса, онда s =70 ∙ 1, 5=105;
t =2 болса, онда s =70·2=140;
t
=3
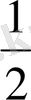 болса, онда s =70 ∙ 3
болса, онда s =70 ∙ 3
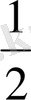 =224.
=224.
Мұндағы аргументтің мәні 1, 5-ке тең болғанда, функцияның мәні 105-ке тең; аргументтің мәні 2-ге тең болғанда, функцияның мәні 140-қа тең; аргументтің мәні
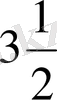 -ге тең болғанда, функцияның мәні 224-ке тең. Функцияның аргументке тәуелділігі
-ге тең болғанда, функцияның мәні 224-ке тең. Функцияның аргументке тәуелділігі

формуласымен анықталады. Мұны кысқаша
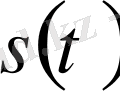 түрінде де жазады. Оқылуы: «тэден эс». Аргументтің мәні және оған сөйкес функцияның мәні: s(1, 5) =105, s (2) =140 және s(
түрінде де жазады. Оқылуы: «тэден эс». Аргументтің мәні және оған сөйкес функцияның мәні: s(1, 5) =105, s (2) =140 және s(
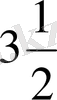 ) =224 түрінде жазылады. Мұндағы жақша ішіндегі аргументтің мәні, теңдіктің оң жағындағы функцияның аргументтің көрсетілген мәніне сәйкес мәні.
) =224 түрінде жазылады. Мұндағы жақша ішіндегі аргументтің мәні, теңдіктің оң жағындағы функцияның аргументтің көрсетілген мәніне сәйкес мәні.
5 - м ы с а л :
у=f(х)
функциясы берілсін, мұндағы
f(x) =x
 . f
(4) -ті табу керек. Ол үшін
f(х)
функциясындағы
х
аргументтің орнына 4-ті қойып есептеу керек:
f
(4) =4
2
=16. Демек,
f
(4) =16.
. f
(4) -ті табу керек. Ол үшін
f(х)
функциясындағы
х
аргументтің орнына 4-ті қойып есептеу керек:
f
(4) =4
2
=16. Демек,
f
(4) =16.
6 - м ы с а л : Аргументтің қандай мәнінде у= 3 х+ 1 функциясының мәні 25-ке тең? у -тің орнына 25-ті коямыз. Сонда x айнымалысы бар теңдеу шығады: 3 x +1=25
3 x =24
x =8.
х= 8 болғанда у= 25 .
7- м ы с а л :
у=f(х)
функциясы берілсін, мұндағы
f(x) =
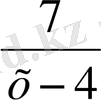 Equation. 3 . f
(6) мәнін
Equation. 3 . f
(6) мәнін
табу керек.
Аргумент:
х
=6 болса,
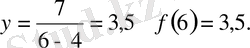
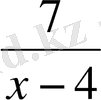 өрнегінің
х
=4 мәнінде мағынасы болмайды. Себебі
х=
4 болғанда
өрнегінің
х
=4 мәнінде мағынасы болмайды. Себебі
х=
4 болғанда
берілген бөлшектің бөлімі нөлге тең.
Демек, аргументтің кез келген мәнінде функцияның мәні анықтала бермейді. Аргумент өзі құрамына енетін формуланың мағынасы болатын мәндерді ғана қабылдай алады.
7-мысалдағы
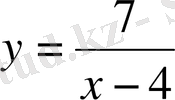 функциясының анықталу аймағы 4-тен басқа барлық нақты сандар. Демек, (-
функциясының анықталу аймағы 4-тен басқа барлық нақты сандар. Демек, (-
 ; 4)
; 4)
 (4; +
(4; +
 ) .
) .
8-м ы с а л :
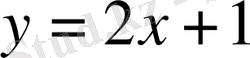 функциясының анықталу аймағы
функциясының анықталу аймағы
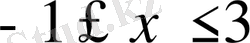 болғандағы функция мәндерінің аймағын табайық.
болғандағы функция мәндерінің аймағын табайық.
Санды теңсіздіктердің қасиеттері бойынша:
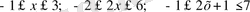 .
.
Демек,
у=
2
х+
1 функциясының анықталу аймағы
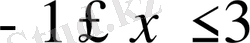 болғандағы оның мәндерінің аймағы [-1; 7] аралығы болады.
болғандағы оның мәндерінің аймағы [-1; 7] аралығы болады.
9 - м ы с а л :
у
=
х
2
функциясының -4<х
 4 анықталу аймағындағы функция мәндерінің аймағы [0; 16] аралығы.
4 анықталу аймағындағы функция мәндерінің аймағы [0; 16] аралығы.
10 - м ы с а л :
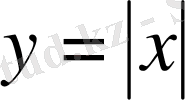 функциясының анықталу аймағы - нақты сандар жиыны немесе (-
функциясының анықталу аймағы - нақты сандар жиыны немесе (-
 ; +
; +
 ) аралығы болса, функция мәндерінің аймағы барлық оң сандар. Демек, [0; +
) аралығы болса, функция мәндерінің аймағы барлық оң сандар. Демек, [0; +
 ) аралығы.
) аралығы.
Кейбір жағдайларда белгілі бір функционалдық тәуелділіктегі, аргумент пен оған сәйкес функция мәндерінің жұбы белгілі бір реттілікпен кесте арқылы көрсетіліп беріледі. Функционалдық тәуелділіктің осылайша берілуі функцияның кестемен берілуі деп аталады. Функция формуламен берілгенде де аргументтің белгілі бір мәніне сәйкес функцияның мәнін тауып, олардың сәйкестігін көрсету үшін кестені пайдаланған қолайлы.
Мысалы, тәулік бойындағы ауа температурасының өзгерісі кестемен берілген.
Уақыт,
t(caғ)
Темпера-
тура, t 0 С
Кестедегі t- уақыт (сағат есебімен) тәуелсіз айнымалы шама (аргумент) . t°С - температура (градус °С есебімен) тәуелді айнымалы шама (функция) .
Демек, функция кестемен берілгенде кестенің бір жолына аргументтің мәні жазылса, екіншісіне оларға сәйкес функцияның мәні жазылады. Кесте тұрақты қадаммен беріледі.
Кестенің қадамы дегеніміз - аргументтің қатар тұрған екі мәнінің айырмасы. Жоғарыдағы кестенің қадамы 2-ге тең. Кестедегі аргументтің мәндері функцияның анықталу аймағындағы мәндер ғана бола алады.
Функцияның кестемен берілуіндегі ескеретін жағдай аргументтің кез келген мәніне сәйкес функция мәні табыла бермейді. Функцияның кестемен берілуін қолдану, тәжірибелер мен бақылау нәтижелеріндегі шамалар арасындағы өзгерісті көрсету (жазу) үшін қажет.
Функция кестемен берілгенде кестеден аргументтің белгілі бір мәніне сәйкес функцияның бір ғана мәнін (есептеусіз) табуға болады.
Айнымалылардың арасындағы функционалдық тәуелділік график ар-қылы да берілуі мүмкін. Мысалы, суды қыздырғанда оның температурасының өзгеруі, темір жол бойымен жолаушы поездарының қозғалысы, еңбек өнімділігінің өзгерісі, т. б.
Функцияны графикпен беру үшін тік бұрышты координаталар жүйесі (Декарттық координаталар жүйесі) қолданылады. Тік бұрышты коорди-наталар жүйесінде аргументтің мәндері және оларға сәйкес функцияның мәндері графиктің бойындағы нүктелермен кескінделеді. Нүктенің абсциссасы аргументтің берілген мәні болса, ординатасы аргументтің берілген мәніне сәйкес функцияның мәні болады.
11 - м ы с а л :
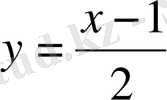 формуласымен берілген функцияның графигін сызайық. Ол үшін алдымен берілген функцияның кестесін құрып алу керек:
формуласымен берілген функцияның графигін сызайық. Ол үшін алдымен берілген функцияның кестесін құрып алу керек:
Координаталары кестеде көрсетілген: А (-3; -2), В (-2; -1, 5), С (-1; -1), D (0; -0, 5), E (1; 0), және F(3; 1) нүктелерін тік бұрышты координаталар жүйесінде белгілеп, оларды сызықпен қосайық (10-сызба) .
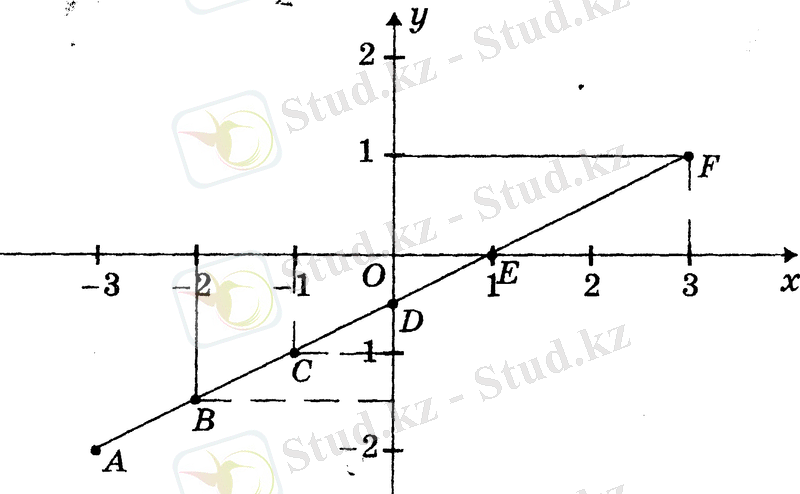
10-сызба
Сонда
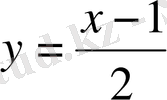 формуласымен берілген функцияның графигі (
АҒ
кесіндісі) сызылады. Мұндағы функцияның анықталу аймағы -3
формуласымен берілген функцияның графигі (
АҒ
кесіндісі) сызылады. Мұндағы функцияның анықталу аймағы -3
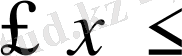 3 немесе [-3; 3] аралығы, ал функция мәндерінің аймағы [-2; 1] аралығы.
3 немесе [-3; 3] аралығы, ал функция мәндерінің аймағы [-2; 1] аралығы.
Графиктегі берілген нүктелер неғұрлым жиі болса, соғұрлым функция графигі дәлірек кескінделеді.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz