Анықталған интегралдарды есептеудің сандық әдістері: тіктөртбұрыш, трапеция және Симпсон формулалары мен компьютерлік жүзеге асуы


ҚАЗАҚСТАН РЕСПУБЛИКАСЫ ҒЫЛЫМ ЖӘНЕ БІЛІМ МИНИСТІРЛІГІ
МАТЕМАТИКА, ФИЗИКА ЖӘНЕ ТЕХНОЛОГИЯЛАР ФАКУЛЬТЕТІ
Математика кафедрасы
КУРСТЫҚ ЖҰМЫС
Тақырыбы: МАТЕМАТИКАНЫ ТЕРЕҢДЕТІП ОҚЫТУДАҒЫ ТУЫНДЫНЫҢ АЛГЕБРАЛЫҚ ҚОЛДАНЫЛУЫ
Жоспар
- Кіріспе
- Негізгі бөлім
1. Анықталған интеграл ұғымы.
1. 1 Анықталған интеграл анықтамасы.
1. 2 Анықталған интегралдың қасиеттері.
2. Анықталған интегралды жуықтап есептеу.
2. 1 Тіктөртбұрыш әдісі.
2. 2 Симпсон әдісі.
3. Анықталған интеграл есептеудің сандық әдістеріне компьютерлік
бағдармаларды құру.
3. 1 Трапеция әдісі.
3. 2 Симпсон әдісі.
III. Қорытынды
Қолданылған әдебиеттер тізімі
Кіріспе.
Интеграл (латынша integer - бүтін) -математиканың маңызды ұғымдарының бірі. Интеграл ұғымы бір жағынан туындысы бойынша функцияны іздеуден, екінші жағынан - ауданды, көлемді және доға ұзындығын өлшеуден, күштің белгілі бір уақыт ішінде атқарған жұмысын табудан шықты. Осыған сәйкесті интеграл анықталмаған және анықталған интерал болып бөлінеді. Міне, осыларды есептеу интегралдық есептеудің міндеті болып табылады. Анықталған интегралды әр түрлі әдістермен шешуге болады. Ал мен анықталған интералдарды есептеудің сандық әдістерін қарастырам.
Әр түрлі физикалық, техникалық, экономикалық және тағы басқа есептерді математикалық әдістерді қолданып шешкенде интеграл астындағы функция немесе оның алғашқы функциясы элементар болмайтын интегралдар жиі кездеседі. Сондықтан, мұндай интегралды жуықтап есептеу әдістерін қарастыруға тура келеді. Тіпті кейбір жағдайларда алғашқы функциясы элементар болатын функцияларды интегралдағанда, Ньютон - Лейбниц ережесінен гөрі жуықтап интегралдау әдістерін қолданған қолайлы болады. Өйткені, Ньютон - Лейбниц формуласы арқылы анықталған интегралды есептеу мүмкіншілігі әрқашан бола бермейді. Анықталған интегралдары болғанымен, оларды алғашқы функциялары арқылы есептеу мүмкіншілігі жоқ. Мұндай жағдайда анықталған интегралды жуықтап есептейді.
Жалпы жуықтап есептеу, соның ішінде интегралды жуықтап есептеу, математиканың дамыған тақырыптарының бірі. Олар әр түрлі идеяларға негізделген. Интегралды жуықтап есептеудің бастапқы идеясы мынада: интеграл астындағы функция онымен кейбір нүктелерде беттесетін көпмүшелікке ауыстырылады, көпмүшеліктің құрылысы қарапайым болумен қатар, интегралы да оңай есептеледі.
Анықталған интегралды есептеудің сандық әдістерін компьютерлік бағдармалар құрып шығаруға болады.
1. Анықталған интеграл ұғымы.
1. 1 Анықталған интеграл анықтамасы.
Аныктама. [а, Ь] кесіндісінде у =f(х) функциясы берілсін.
а) [а, b] кесіндісін кез-келген а=х о <Х 1 <X 2 < . . . <Х п =b
нүктелерімен [х j ., х j+1 ] . і = 0, 1, . . . , n - 1, боліктерге болеміз
(оны R бөліктеуі деп атайык) ;
б) Әрбір [х j ., х j+1 ] бөліктен кез-келген ξ j ∈[х j ., х j+1 ]
нүктелерін алып, f функциясының R - бөліктеуіне сәйкес интегралдық қосынды деп аталатын
S R ( f ) =
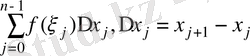
қосындыны құрамыз;
в)
→ 0 ұмтьлдырып интегралдық қосындьның шегін аламыз.
Егер бұл шек бар болса , онда ол f функциясының
[а, Ь] кесіндісіндегі анықталған интегралы деп аталады да
(a<b)
(1)
түрінде белгіленеді. Мұндағы а мен b сандары - анықталған интегралдың сәйкес төменгі және жоғарғы шегі
деп аталады.
Егер f фунщиясы [а, b] кесіндісінде узіліссіз болса, онда оның интегралдық қосындысының шегі бар.
Анықталған интегралды оның анықтамасы арқылы есептеу күрделі жүмыс. Сондықтан анықталған интегралды есептеудің басқа тәсілін табу қажет болды. Ньютон мен Лейбниц математикалық аначиздің маңызды үғымдары интеграл мен туындыны байланыстыратын теореманы дәлелдеді. Оның түйіні мынау: егер f(х) функциясы [а, b] кесіндісінде үзіліссіз, ал Ғ(х) оның осы кесіндідегі қандай да бір алғашқы функциясы (Ғ'(х) = f(х) ) болса, онда Ньютон-Лейбниц формуласы деп аталатын
= Ғ(b) -Ғ(а) (2)
тендік орындалады.
1. 2. Анықталған интегралдардың касиеттері
1°. Егер ∀ х∈[а, Ь], f(х) ≡ 1 болса, онда
(3)
Шынында да, [a, b] кесіндісінің кез-келген R бөліктеуі үшін

шығады.
2°. Егер [a, b] кесіндісінде f және g интегралданатын функциялар, ал А, В - кез-келген сандар болса, онда
(4)
Кез-келген R бөліктеуі үшін
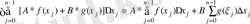
тендігі орындалады. Бұдан
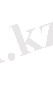
0 ұмтылдырып
шекке өтсек, (4) теңдікті аламыз. (4) теңдіктің b < а үшін де дүрыс екенін байқауға болады.
Дербес жагдайда, b = 0 болса, онда
Equation. 3 (5)
ал А = 1, B = 1 болса, онда
(6)
Ескерту. Егер f (х), g (х) функциялары кесіндісінде интегралданатын болса, оңда f (х) * g (х) көбейтіндісі де осы кесіндіде интегратданады. Бірақ кебейтіндінің интегралы көбейткіштердің интегралдарының көбейтіндісіне тең бола бермейді
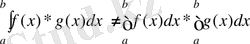
Анықтама бойынша, а нүктесінде берілген кез-келген функциясы үшін
(7)
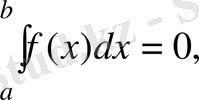
ал [а, b] кесіндісінде интегралданатын f функциясы үшін
Equation. 3 (8)
деп аламыз. Бұл теңдіктер геометриялық тұрғыдан оңай көрініп түр. Шыныңда да, бірінші жағдайда, қисық сызықты трапеция, [0, f (а) ] кесіндісіне айналады да, оның ауданы нөлге тең болады; екінші жағдайда, кесіндіні бөліктеу нүктелері үшін а = х 0 > х 1 > . . . > х n-1 > х п = b
орындалады (b < а) және әрбір ∆х j үшін
∆х j = Х j+1 - X j < 0, i= 0, 1, . . . , п - 1 болатынын ескеру керек.
3°. (анықталган интегралдың аддитивтік қасиеті) . Егер кез-келген а, b, с сандары үшін әрбір [а, b], [а, с] және [с, b] кесінділерінде f интегралданатын функция болса, онда
Equation. 3 (9)
теңдігі орындалады.
1) а < с < b болсын. [а, b] кесіндісін с нүкгесі бөліктеу нүктесі с = х т болатындай етіп R бөліктеуін жасайық
R: а = х о <х 1 < . . . <х т =с< . . . <х п =b.
Осы R бөліктеуінен [а, с] мен [с, b] кесінділерінің
R 1 : а = х о <х 1 < . . . <х т =с,
R 2 : с = х т <х т+1 < . . . <х п =b
бөліктеулері пайда болады.
Олай болса,
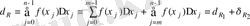
Бұдан
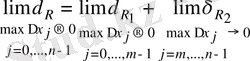
теңдігін жаза аламыз.
3 0 қасиеттің шарты бойынша бұл үш шектің үшеуі де бар, сондықтан соңғы теңдік (9) теңдік түрінде жазылады.
2) а<b<с болсын. Онда (9) теңдік бойынша
, ал бұдан (8) теңдікті ескеріп,
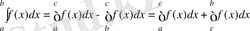
аламыз.
Ескерту. 3 0 касиеттің орындалуъі үшін f(х) функциясы [а, b], [а, с], [с, b] кесінділерінің ең үлкенінде интегралдануы жеткілікті.
1-теорема . Кесіндінің бір нүктесінен басқа нүктелерінде нөлге тең болатын функцияның осы кесіндідегі анықталған интегралы нөлге тең. Басқаша айтканда,
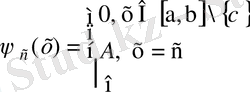 (10)
(10)
функциясы үшін
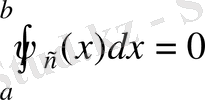 (11)
(11)
[a, b] кесіндісіне кез-келген R бөліктеуін жасайық
R: а = х 0 <х 1 < . . . <х п =b.
с нүктесі осы бөліктердің біреуінің, айталық [х т ,, х т+1 ] бөлігінің ішінде жатсын (х т ≤ с < х m+1 ) . Онда
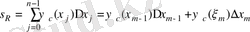
∀x∈[a, b] нүктелері үшін ψ с (x) ≤A болатындықтан, δ R =ψ c (ξ m-1 ) ∆x m-1+ ψ c (ξ m ) ∆x m ≤∆x j >0ескерсек≤ψ с (ξ m-1 ) *∆x m-1 +
+ψ
c
(ξ
m
) ∆x
m
≤A*(∆x
m-1
+∆x
m
) →A*0,
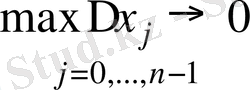
яғни (11) теңдік орындалады.
2-теорема. Егер [а, b] кесіндісінде интегралданатын f функциясының с∈[а, b] нүктесіндегі мәнін өзгертсек, онда өзгергеннен кейін алынған f 1 функдиясы үшін
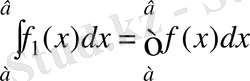
тендігі орындалады. .
f функциясын жалғыз с нүктесінде өзгерту, оған ψ c (x) функциясын ((10) -қараңыз) қосу деген сөз:
.
Олай болса, осы тендіктен (6) және (11) тендіктерін ескеріп,
аламыз.
Бұл теоремадан ƒ функциясының интегралдануы оның белгілі бір нүкгеде қандай мән қабылдайтынына тәуелді емес екенін көреміз.
4 0 . Егер [а, Ь] кесіндісінде ƒ, g интегралданатын функциялар болса және \/х∈[а, Ь], f(х) ≤ g(х)
теңсіздігі орындалса, онда
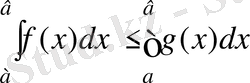 , а≤b. (12)
, а≤b. (12)
Кез-келген R бөліктеуі үшін ∆х j ≥ 0 екенін ескеріп
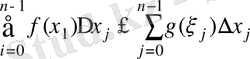
аламыз. Бүл теіңсіздіктен mах ∆х j - > 0 үмтьшдырып (12) -теңсіздікті аламыз.
Дербес жагдайда, егер f теріс емес, [а, Ь] кесіндісінде
интегралданатын функция болса, онда,
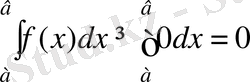 , а≤b, яғни ∀х∈[а, b], f(x) ≥0 үшін
, а≤b, яғни ∀х∈[а, b], f(x) ≥0 үшін
, а ≤b. (13)
5°. Егер f, f функциялары [а, Ь] кесіндісінде интегралданатын болса, онда
 Equation. 3
Equation. 3
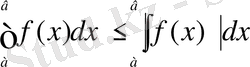 Equation. 3 . (14)
Equation. 3 . (14)
∀х∈[а, Ь] нүктелері үшін -ƒ(х) ≤ƒ(х) ≤ƒ(х)
теңсіздіктері орындалатыны айқын. Бүдан (12) және (5) қатыстарды пайдаланып
, а≤b, немесе
, а
в, яғни
, а
в, аламыз.
Егер а>в болса, онда осы соңғы теңсіздікпен (8) тендікті пайдаланып
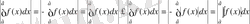 аламыз.
аламыз.
Дәлелдеу барысында алынған
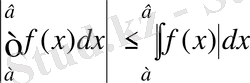 , а
, а
 в. (14)
в. (14)
теңсіздігі математикада жиі пайдаланылады.
Ескерту. Егер f функциясы [а, в] кесіндісінде интегралданса, онда
функциясы да осы кесіндіде интегралданады. Бірақ, керісінше,
функциясы
кесіндісінде интегралданса,
функциясы да осы кесіндіде интегралданады деп айта алмаймыз.
3-теорема . ƒ функциясы
кесіндісінде интегралданатын теріс емес функция болсын. Егер ƒ функциясы с∈
нүктесінде үзіліссіз және f(x) > 0 болса, онда
, а<в (15)
теңсіздігі орындалады.
2. Анықталған интегралдарды жуықтап есептеу.
Жуықтап интегралдау әдісі кез-келген үзіліссіз (функцияның анықталған интегралының жуық мәнін жеткілікті дәлдікпен табуға мүмкіндік береді. Кез-келген үзіліссіз функцияның алғашкы функциясы элементар функциялар арқылы өрнектеле бермейтіндігі осыдан . Анықталған интегралды жуықтап есептеу қажеттігі: интегралдың сол мәнін табу мүмкін емес немесе оны табу оліс; белгісіз жағдайларда да туады.
Қарастырылатын жуық сандық әдістер мынаған негізделген: интеграл мәнін қандай да бір қисық сызықты трапеция ауданы деп алып, басқа қисық сызықты трапеция ауданын табамыз. Бұл трапецияның қисық сызығын бастапқы трапецияның қисық сызығынан аздап қана "ауытқитындай" және бұл соңғы трапеция ауданы оңай есептелетіндей етіп аламыз.
2. 1.
Тік төртбұрыштардың және трапециялардың квадратуралық формулалары.
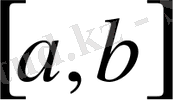 кесіндісін а=х
0
<х
1
<х
2
…<х
n
=b нүктелерімен әрқайсысының ұзындығы ∆х болатын өзара тең n бөлікке бөлеміз. Онда
кесіндісін а=х
0
<х
1
<х
2
…<х
n
=b нүктелерімен әрқайсысының ұзындығы ∆х болатын өзара тең n бөлікке бөлеміз. Онда
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz