Тербелістер теориясы: маятниктер, гармониялық тербелістер және суперпозициялық құбылыстар


Физикалық маятник
Физикалық маятник деп оның инерция центріне дәл келмейтін қозғалмайтын нүкте маңында ауырлық күшінің әсерінен тербеліс жасай алатын қатты денені айтады.
Маятник тепе-теңдік қалпынан α бұрышқа ауытқығанда, оны тепе-теңдік қалпына қайтаруға тырысатын айналдырушы момент пайда болады.


Екінші жағынан, өте аз бұрышта

мұндағы J - O іліну нүктесінен өтетін оське салыстырғандағы маятниктің инерция моменті;
l - іліну нүктесі мен С масса центрінің ара қашықтығы;
 - кері қайтарушы күш (минус таңбасы күштің ауытқу бұрышы
α
-ның үлкею бағытына қарама-қарсы бағытталатынын көрсетеді) .
- кері қайтарушы күш (минус таңбасы күштің ауытқу бұрышы
α
-ның үлкею бағытына қарама-қарсы бағытталатынын көрсетеді) .
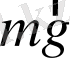
L
l
O
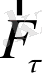
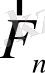
C
O΄
α
Олай болса,
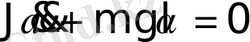 немесе
немесе
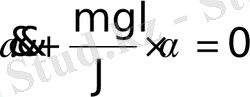
Осыдан, тепе-теңдік қалпынан әлсіз тербеліс жасаған кезде физикалық маятник гармониялық тербеліс жасайды:

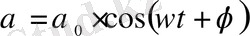
Циклдік жиілігі мен сәйкес периоды:
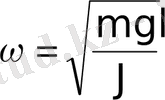 ,
,
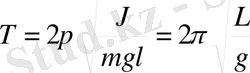
мұндағы,
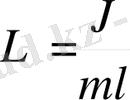 - ұзындығы физикалық маятниктің келтірілген ұзындығы деп аталады.
- ұзындығы физикалық маятниктің келтірілген ұзындығы деп аталады.
Физикалық маятниктің келтірілген ұзындығы деп периоды берілген физикалық маятниктің тербеліс периодындай болатын математикалық маятниктің ұзындығын айтады. Айналу осінен келтірілген ұзындыққа тең қашықтықта жатқан іліну нүктесін инерция центрімен қосатын түзудегі нүкте (О ' ) физикалық маятниктің теңселу центрі деп аталады.
Математикалық маятникті массасы оның масса центрінде шоғырланған физикалық маятниктің дербес жағдайы деп қарастыруға болады. Осыдан
J=ml
2
, олай болса,
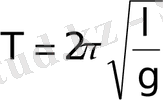 .
.
Гармониялық тербелістерді қосу
Егер жүйеде бір уақытта бірнеше тербелмелі процестер қатысатын болса, онда осы тербелістерді қосу қорытқы тербелмелі процессті анықтайтын тербеліс заңын табу болып табылады.x
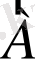
φ 2 -φ 1
φ
φ 2
φ 1
x 1
x 2
x
х 1 және х 2 тербелістерді қосу үшін векторлық диаграмма әдісін қолданамыз
х 1 =A 1 cos (ωt+ϕ 1 ) , х 2 =A 2 cos (ωt+ϕ 2 )
А
1
және
А
2
векторлары бірдей бұрыштық жылдамдықпен айнала-тындықтан, олардың арасындағы фазалар айырымы
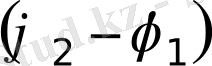 тұрақты болып қалады.
тұрақты болып қалады.
Қорытқы тербелістің теңдеуі:
х=х 1 +х 2 =A cos (ωt+ϕ)
мұндағы, А амплитудасы мен ϕ бастапқы фазасы мына қатынастар арқылы беріледі:
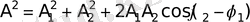 ,
,
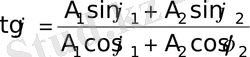
Тербеліс жиілігі бірдей және бағыттас екі гармониялық тербелістің қосындысы жиілігі мен бағыты сондай гармониялық тербеліс болады.
Қорытқы тербелістің амплитудасы қосылатын тербелістердің фазаларының айырымына тәуелді:
- , мұндағы, ондаА=А1+А2
- , мұндағы, ондаА=А1+А2
Соғу
Соғу деп жиіліктері аздап өзгешелеу екі гармониялық тербелістердің қосылуынан тербеліс амплитудасының периодты түрде өзгеруін айтады.
Қосылатын тербелістердің амплитудасы А , ал жиіліктері ω және ω+∆ω, және де ∆ω<<ω болсын.
Санақтың басында екі тербелістің бастапқы фазалары нольге тең деп таңдап алайық:
х 1 =A cos ωt, х 2 =A cos (ω+∆ω) t
Қорытқы тербелістің түрі мынадай болады:
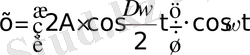
- яғни, амплитудасы
ω
соғу
 жиілікте
А
соғу
жиілікте
А
соғу
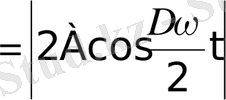 теңдеуімен өзгеретін
ω
жиіліктегі гармониялық тербеліс (соғу жиілігі косинустың өзгеру жиілігінен екі есе үлкен, өйткені
А
соғу
модулі бойынша алынады)
теңдеуімен өзгеретін
ω
жиіліктегі гармониялық тербеліс (соғу жиілігі косинустың өзгеру жиілігінен екі есе үлкен, өйткені
А
соғу
модулі бойынша алынады)
Тербелістер деп белгілі бір дәрежеде қайталанып отыратын процестерді айтады. Қайталанын процестің физикалық табиғатына байланысты тербелістер: механикалық, электромагниттік, электрмеханикалық және т. б. түрге бөлінеді.
Тербелмелі жүйеге жасалатын әсердің сипатына қарай еркін тербелістер, еріксіз тербелістер, автотербелістер және параметрлік тербелістер деп ажыратылады.
Еркін тербелістер деп қозғалысқа келтірілгеннен кейін немесе тепе-теңдік қалпынан шығарылғаннан соң жүйеге сырттан әсер етпейтін жағдайдағы тербелісті айтады.
Еріксіз тербелістер деп сыртқы күштердің әсерінен болатын тербелісті айтады.
Автотербелістерге сыртқы әсерді жүйенің өзі басқаратын (физикалық маятник) тербелістер жатады.
Параметрлік тербелістер кезінде сыртқы әсер салдарынан жүйенің қандай да болсын параметрі, мысалы тербеліс жасап тұрған шарик ілінген жіптің ұзындығы, периодты түрде өзгерсе.
Гармониялық тербелістер деп уақыт бойынша синус немесе косинус заңына сәйкес өзгеретін тербелістерді айтады.
Тербелмелі қозғалысты сипаттап шығу үшін пружинаға ілінген, массасы m шариктен тұратын жүйені қарастырайық.
Еркін тербелістер
Тербелістер деп белгілі бір дәрежеде қайталанғыштығымен айқындалатын қозғалысты немесе процесті айтады.
Тербеліс кезінде энергияның бір түрінің екінші түріне айналуы қабаттаса жүреді.
Еркін немесе меншікті тербелістер деп қозғалысқа келтірілгеннен кейін немесе орнықты қалпынан шығарылғаннан соң өзімен-өзі қалатын жүйеде өтетін тербелістерді айтады.
Еріксіз тербелістер деп тербелмелі жүйе периодты түрде өзгеріп отыратын сыртқы күштің әсеріне кез болатын тербелістерді айтады.
Физикалық табиғатына байланысты тербелістер: механикалық, электромагниттік және т. б. бөлінеді.
Бірақ, әртүрлі тербелмелі процестер бірдей теңдеулермен анықталады, сондықтан, барлық тербелмелі процестерді тербелістердің жалпы қасиеттерін қолдана отырып зерттеу тиімді.
Гармониялық тербелістер және олардың сипаттамасы
Гармониялық тербеліс деп тербелістің физикалық шамалары уақыт бойынша синус немесе косинус заңдары бойынша өзгеретін тербелісті айтады.
Әртүрлі периодты процестерді (бірдей уақыт мезеттерінде қайталанып отыратын процестер) гармониялық тербелістердің қосындысы (суперпозициясы) түрінде беруге болады.
S шамасы бойынша гармониялық тербеліс теңдеуі мынадай түрде болады:
S=A⋅ cos (ωt+ϕ)
мұндағы: А - тербеліс амплитудасы − жүйенің тепе-теңдік қалпынан ең үлкен ауытқуы;
ω - дөңгелектік (циклдік) жиілік;
ϕ - тербелістің t=0 уақыт мезетіндегі бастапқы фазасы;
(ωt+ϕ) - тербелістің t уақыт мезетіндегі фазасы.
Тербеліс фазасы тербелмелі шамалардың берілген уақыт мезетіндегі мәнін анықтайды. Косинус +1-ден -1 аралығында өзгеретіндіктен, S- тің мәні +А дан -А -ға дейінгі аралықта жатады.
cos (α+2π) = cos α болғандықтан, 2π бүтін санын фазаға қосқанда немесе одан алып тастағанда гармониялық тербеліс кезінде S- тің мәні өзгермейді.
Толық бір тербеліс жасау үшін кеткен уақыт аралығымен өлшенетін шама тербеліс периоды деп аталады және тербеліс фазасы 2π- ге өсімше қабылдайтындықтан
ω(t+T) +ϕ=(ωt+ϕ) =2π
осыдан
T
=
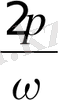 ;
;
Периодқа кері шама, бірлік уақыт ішіндегі тербеліс саны n тербеліс жиілігі деп аталады
ν=
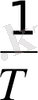 =
=
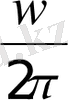 .
.
Тербеліс жиілігінің өлшем бірлігі - герц ( Гц ) периодты процестің жиілігі - периоды 1 секундқа тең келетін тербеліс санымен өлшенеді.
Гармониялық тербелістің дифференциалдық теңдеуі
S=A ⋅cos (ωt+ϕ) гармониялық тербелмелі S шамасының уақыт бойынша бірінші (жылдамдық) және екінші (үдеу) туындылары да сондай дөңгелектік жиілікпен гармониялық заң бойынша өзгереді:
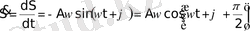
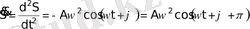


соңғы теңдіктен, S шамасының мына теңдеулерді қанағаттандыратынын көреміз:
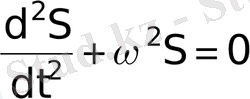 немесе
немесе
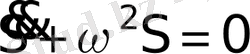
Осы теңдеу гармониялық тербелістің дифференциалдық теңдеуі деп аталады.
Оның шешуі: S=A⋅ cos (ωt+ϕ)
x
0
φ
s
ω
Векторлық диаграмма әдісі
Гармониялық тербелістер амплитуда векторының айналу немесе векторлық диаграмма әдісімен кескінделеді. Х осінің кез-келген О нүктесінен, осьпен тербелістің бастапқы фазасына тең ϕ бұрыш жасайтын, модулі қарастырылып отырған тербеліс амплитудасы
А
-ға тең,
 векторын салайық. Егер осы вектор О нүктесінің айналасында
ω
бұрыштық жылдамдығымен айналса, вектордың проекциясы Х осінде
S=A⋅
cos
(ωt+ϕ)
заңы бойынша тербеліс жасайды.
векторын салайық. Егер осы вектор О нүктесінің айналасында
ω
бұрыштық жылдамдығымен айналса, вектордың проекциясы Х осінде
S=A⋅
cos
(ωt+ϕ)
заңы бойынша тербеліс жасайды.
Х әрпімен белгіленген осьті алайық. Осьтің бойынан алынған О нүктесінен
Осьпен α бұрыш жасайтын ұзындығы а векторын саламыз. Егер бұл векторды 𝙬 бұрыштық жылдамдықпен айналысқа келтірсек, онда вектор ұшының проекциясы Х осі бойынша -А-дан +А - ға дейінгі аралықта қозғалады. Әрі бұл проекцияның координатасы уақыт бойынша мына заңмен өзгереді:
Мұнан гармониялық тербелістің ұзындығы тербеліс амплитудасына тең, а вектордың бағыты х осімен тербелістің бастапқы фазасына тең бұрыш жасайтындай вектор арқылы беруге болатыны көрінеді.
Гармониялық тербеліс жасайтын материалдық нүктенің энергиясы
Материалдық нүктенің кинетикалық энергиясы:
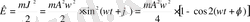
Квазисерпімді күштің әсерінен гармониялық тербеліс жасайтын материалдық нүктенің потенциалдық энергиясы:
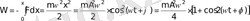
Толық энергия
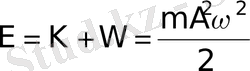 тұрақты болып қалады және уақыттың өзгеруіне байланысты кинетикалық энергия потенциалдық энергияға және керісінше ауысып отырады.
тұрақты болып қалады және уақыттың өзгеруіне байланысты кинетикалық энергия потенциалдық энергияға және керісінше ауысып отырады.
Гармониялық осциллятор
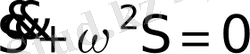 теңдеуімен сипатталатын жүйе гармониялық осциллятор деп аталады.
теңдеуімен сипатталатын жүйе гармониялық осциллятор деп аталады.
Гармониялық осцилляторға мысал ретінде пружиналық, математикалық және физикалық маятниктерді және электрлік тербелмелі контурды алуға болады.
Пружиналық маятник
Пружиналық маятник деп абсолют серпімді пружинаға ілінген және F=-kx серпімді күштің әсерінен гармониялық тербеліс жасайтын m массалы жүкті айтады. Мұндағы, k - пружинаның қатаңдығы.
0
x
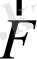
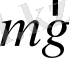
Маятниктің қозғалыс теңдеуі:
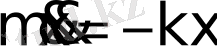 немесе
немесе
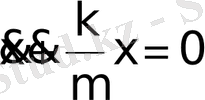 .
.
Осы теңдеуді гармониялық осциллятордың
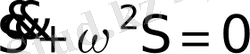 теңдеуімен салыстырып, пружиналық маятник те
x=A⋅
cos
(ωt+ϕ)
заңы бойынша
теңдеуімен салыстырып, пружиналық маятник те
x=A⋅
cos
(ωt+ϕ)
заңы бойынша
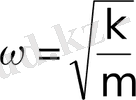 циклдік жиілікпен және
циклдік жиілікпен және
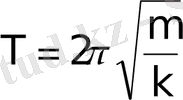 периодпен тербелетінін көреміз.
периодпен тербелетінін көреміз.
Пружиналық маятниктің потенциалдық энергиясы
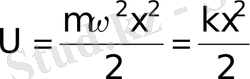
егер маятникке жылдамдыққа пропорционал үйкеліс күші әсер етсе,
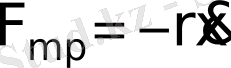 , мұндағы,
r
- кедергі коэффиценті, ал маятник тербелісі өшетін тербеліс болады және маятник қозғалысының заңы
, мұндағы,
r
- кедергі коэффиценті, ал маятник тербелісі өшетін тербеліс болады және маятник қозғалысының заңы
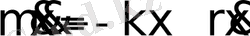 немесе
немесе
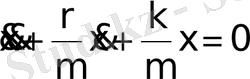 түрінде болады.
түрінде болады.
Математикалық маятник
Математикалық маятник деп салмақсыз және созылмайтын жіпке ілінген, массасы бір нүктеге жинақталған, ауырлық күшінің әсерінен тербеліс жасайтын идеалданған жүйені айтады.
Ұзын жіпке ілінген шағын ауыр шарик едәуір дәрежеде математикалық маятникке жақындайды.
α
ауытқу бұрышының аз мәнінде
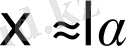 деп алуымызға болады.
деп алуымызға болады.
х
l
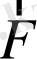
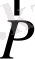
0
α
Кейін қарай қайтарушы күш:
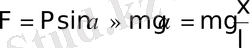
Қозғалыс теңдеуі:
 немесе
немесе
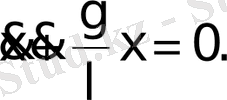
Олай болса, математикалық маятниктің қозғалысы гармониялық тербелістің дифферен-циалдық теңдеуімен анықталады, яғни тербеліс жиілігі мен периоды сәйкес:
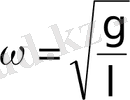 ,
,
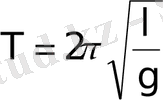
болатын x=A⋅ cos (ωt+ϕ) заңы бойынша орындалады. Тербеліс жиілігінің теңдеуінен, математикалық маятниктің тербеліс жиілігі маятниктің ұзындығы мен еркін түсу үдеуіне байланысты болады, ал маятник массасына тәуелді болмайды.
Фурье жіктелуі
Кез-келген S=f(t) күрделі периодты тербелісті циклдік жиілігі ω 0 циклдік жиілікке еселі болатын жәй гармониялық тербелістердің қосындысы түрінде беруге болады:
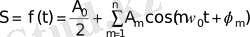
f(t) периодты функциясын осылайша жіктеу Фурье қатарына жіктеу немесе күрделі периодты тербелістің гармониялық анализі деп аталады.
Циклдік жиіліктері ω 0 , 2ω 0 , 3ω 0 және т. б. жиіліктерге сәйкес келетін Фурье қатарының мүшелері күрделі периодтық S=f(t) тербелісінің бірінші (немесе негізгі), екінші және т. б. гармоникалары деп аталады.
Осы гармоникалардың жиынтығы S=f(t) тербеліс спектрін құрайды.
Жиіліктері бірдей өзара перпендикуляр гармониялық тербелістерді қосу
Жиіліктері ω бірдей, екі гармониялық тербеліс өзара перпендикуляр х және у осінің бойында таралсын. Санақ басын бірінші тербелістің бастапқы фазасы нольге тең болатындай етіп таңдап алайық:
x=Acosωt, y=Bcos(ωt+α)
мұндағы α - тербеліс фазасының айырмасы, ал А мен В - олардың амплитудасы.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz