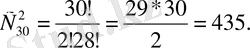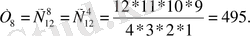Математикалық индукция, комбинаторика және функциялардың негізгі қасиеттері


МАТЕМАТИКАЛЫҚ ИНДУКЦИЯ
Математикалық индукция әдісі. Математикалық тұжырым натурал сандар жиынында берілуі мүмкін: (
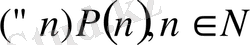 .
Мұндай тұжырым немесе сөйлем көбінесе математикалық
индукция
әдісімен дәлелденеді. Бұл әдіс келесі математикалық индукция принципіне негізделген.
.
Мұндай тұжырым немесе сөйлем көбінесе математикалық
индукция
әдісімен дәлелденеді. Бұл әдіс келесі математикалық индукция принципіне негізделген.
Егер төмендегі екі шарт орындалса, онда Р(п) сөйлемі п айнымалдың кез келген натурал мәндері үшін шын:
1) Р(п) сөйлемі п =1 мәні үшін шын;
2) "Р(п) сөйлемі п =к мәні үшін шын (к - кез келген натурал сан) "деп қабылданған ұйғарымнан, оның келесі п = к + 1 мәні үшін де шын екені шығады.
1-мысал. Келесі сөйдемді дәлелдеу керек:
▼
Р(п)
= {5-2
3n-2
+ 3
3n-1
саны 19-ға бөлінеді,
п
 Equation. 3 N }.
Equation. 3 N }.
1) Егер п =1 болса, онда Р(1) = { 5-2 +3 2 = 19 саны 19-ға бөлінеді} - шын сөйлем;
2) "
п
=
к
мәні үшін
Р {к) =
{5-2
2к-2:
+З
3к-1
"'саны 19-ға бөлінеді,
к
 N
}"- шын деп ұйғарайық. Онда
N
}"- шын деп ұйғарайық. Онда
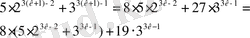
болатындықтан Р {к+1) сөйлемі де шын. Өйткені, мұндағы бірінші қосылғыш ұйғарым бойынша 19-ға бөлінеді, ал екінші қосылғыш - көбейткішінің бірі 19 тең көбейтінді, ол 19-ға бөлінеді. Математикалық индукция принципінің екі шарты да орындалғандықтан, Р (п) сөйлемі п айнымалдың кез келген натурал мәндері үшін шын.
Математикалық индукция әдісімен, п = m -нен басталған бүтін сандар жиынында берілген сөйлемді де дәлелдеуге болады. Егер мұндағы т теріс бүтін сан болса, онда п = - т ауыстыруы жасалады.
2-мысал. Теңсіздікті дәлелдеу керек:
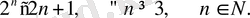
▼1) Егер п=3 болса, онда 2 1 > 2*3 + 1, яғни Р (3) - шын;
2) Кез келген к натурал саны үшін Р (к) шын, яғни 2 к > 2к +1 теңсіздігі орындалсын. Онда
2*2 к >2*(2к +1), (1)
ал 2*(2к + і) = 4к + 2 = 2(к + 1) + 1 + (2к-1) >2(к + 1) + 1, өйткені к>1 мәндері үшін 2к-1>0. Олай болса, (1) теңсіздіктен 2 к+1 >2*(к + 1) + 1, яғни Р( к) => Р(к+1) .
Сонымен, математикалық индукция принципінің екі шарты да орындалғандықтан берілген теңсіздік кез келген п > 3 мәндері үшін дұрыс.
2. Комбинаторика. Комбинаторика дегеніміз - ақырлы жиын элементтерін белгілі бір ретпен орналастыру, бөліктеу, т. с. с. сияқты жасалатын амалдар. Кейбір комбинаторикалық есептерде жиын элементтерінің орналасу реті маңызды роль атқаруы мүмкін (мысалы, жауынгерлердің сап түзеп түру реті) . Бұл жағдайда, мысалы {а, в, с}, {в, а, с} екі түрлі жиын ретінде қаралады. Бірақ бұл екі жиын бірдей элементтерден құралған ақырлы жиындар болғандықтан, олар анықтама бойынша, өзара тең екені белгілі. Осындай қайшылықтар болмас үшін комбинаторикалық есептерде "кортеж", " п - өлшемді вектор", "сөз" сияқты атаулар қолданылады. Онда жоғарыдағыдай екі жиынды (а, в, с), (в, а, с) символымен белгілейді және оларды екі түрлі кортеж деп санайды.
Ал біз "кортеж" терминінің орнына "ретгелген жиын" терминін қолданамыз, яғни есептегі қарастырылатын реттелген жиындардың элементтерінің орналасу реті бірдей болмаса, олар әртүрлі жиын деп саналады.
Орналастыру. п - элементті жиын берілсін. Оның к-элементті әрбір реттелген ішжиыны п - элементтен к-элемент бойынша орналастыру деп аталады.
Мысалы, {а, в, с} - 3-элементті жиынның к - 2 элемент бойынша орналастырулары: (а, в), (а, с), (в, с), (в, а), (с, а), (с, в) .
Сонымен, орналастырулар не элементтерінің құрамы бойынша, немесе элементтерінің орналасу реті бойынша ажыратылады.
Анықтамадан,
п
 к
к
 0 екенін көреміз. Егер
к
= 0 болса, онда
п -
элементті жиынның 0 - элементті ішжиыны, яғни бос жиын болады.
0 екенін көреміз. Егер
к
= 0 болса, онда
п -
элементті жиынның 0 - элементті ішжиыны, яғни бос жиын болады.
п -
элементтен
к -
элемент бойынша орналастырулардың барлық саны
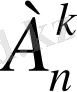 символымен белгіленеді
(А -
француздың "аrrаngеment" - "ретке келтіру" сөзінің бірінші әрпі) .
символымен белгіленеді
(А -
француздың "аrrаngеment" - "ретке келтіру" сөзінің бірінші әрпі) .
Мысалы, жоғарыда 3-элементті {а, в, с} жиынының
к
= 2 элемент бойынша орналастыруларының жалпы саны
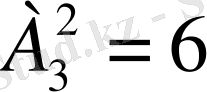 екенін көрдік. Ал,
екенін көрдік. Ал,
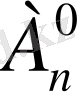 = 1 екені анық, өйткені, кез келген жиын үшін оның бірде-бір элементі жоқ ішжиыны (бос жиын) - біреу.
= 1 екені анық, өйткені, кез келген жиын үшін оның бірде-бір элементі жоқ ішжиыны (бос жиын) - біреу.
Жалпы жағдайда келесі теорема орын алады.
Теорема .
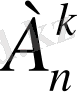 =п(п-1) (п-2) - . . . -(п-к +1) .
(2)
=п(п-1) (п-2) - . . . -(п-к +1) .
(2)
▼
к
- элементті реттелген ішжиынның бірінші элементін тандап алуға
п
-мүмкіндік (тәсіл) бар. Бірінші элемент таңдап алынған соң, оның екінші элементін таңдауға
(п-
1) мүмкіншілік (тәсіл) қалады. Ал осы алғашқы екі элементті таңдап алу мүмкіншілігі
п (п -
1) тең. Алғашқы екі элемент таңдап алынған соң үшінші элементті алуға
(п -
2) мүмкіншілік қалады. Ал алғашқы үш элементті тандап алу тәсілі
п(п -
1 ) (
п
-2) . Осылайша, алғашқы (к-1) элемент тандалса,
к-ші
элементті таңдауға
п - (к -
1)
= п - к +
1 мүмкіншілік қалады. Ал осы алғашқы
к
элементті тандап алу тәсілі, яғни
п-
элементтен к-элемент бойынша орналастырулар саны -
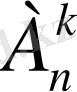 =
п(п
- 1) (
п
- 2) • . . . •(
п-
к
+ 1) .
=
п(п
- 1) (
п
- 2) • . . . •(
п-
к
+ 1) .
2) формуланы келесі түрде жазуға болады
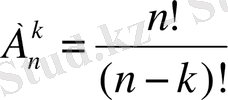 (4)
(4)
(мұндағы п != 1 • 2 • 3• . . . • ( п - 1) • п , яғни п - алғашқы п натурал сандардың көбейтіндісі, ол "эн факториал" деп оқылады) .
Шынында да,
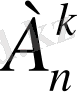 =
п(п
- 1) (
п
- 2) • . . . •(
п-
к
+ 1) =
=
п(п
- 1) (
п
- 2) • . . . •(
п-
к
+ 1) =
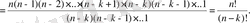
Мысал. Ауылдың 3001 тұрғындарынан бір әкім мен оның бір орынбасарын неше тәсілмен таңдауға болады?
▼
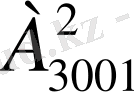 = 3001 • 3000 = 9003000 .
= 3001 • 3000 = 9003000 .
Алмастырулар.
Анықтама. п - элементтен п -элемент бойынша орналастыру п - элементтен жасалған алмастыру деп аталады.
Сонымен, алмастыру-орналастырудың к = п мәніне сәйкес дербес жағдайы.
Алмастырулардағы элементтердің құрамы бірдей, өйткені оның әрбіреуінде барлық п элемент бар. Сондықтан олар бір бірінен тек элементтерінің орналасу реті бойынша ғана ажыратылады. к-элементтен жасалған алмастырулардың жалпы саны Р п арқылы белгіленеді (Р - француздың "реrmutation" - "алмастыру" сөзінің бірінші әрпі) және
Р n =п! (2)
▼ (1) - формулада к=п деп алып (2) -формуланың дұрыстығына көз жеткізіңіз.
Мысал. Шақырылған 8 қонақты 8 орындыққа неше тәсілмен отырғызуға болады?
▼ Р 8 =8!=1-2-3-4-5-6-7-8 = 40320.
Ескерту.
Егер
к= п
болса, онда (1) және (2) формулаларынан
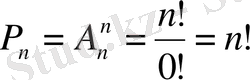 аламыз. Әрине, бұл теңдік орындалуы үшін 0!=1 болуы тиіс.
аламыз. Әрине, бұл теңдік орындалуы үшін 0!=1 болуы тиіс.
Мұндай қорытындыға басқа жолмен де келуге болады:
п
 2
үшін
п! = (п -
1) ! •
п
тендігі орындалады. Бұл тендік
п
= 1 үшін де орындалуы үшін (яғни 1! = 0! • 1 тендігі дұрыс болуы үшін) 0! = 1 болуы тиіс.
2
үшін
п! = (п -
1) ! •
п
тендігі орындалады. Бұл тендік
п
= 1 үшін де орындалуы үшін (яғни 1! = 0! • 1 тендігі дұрыс болуы үшін) 0! = 1 болуы тиіс.
Терулер.
Анықтама. п - элементті жиынның әрбір к- элементті ішжиыны п - элементтен к - элемент бойынша теру деп аталады.
Сонымен, анықтама бойынша, к - элементті терулер элементтерінің тек қана құрамы бойынша ажыратылады. Мысалы, 3-элементті {а, в, с} жиынының к=2 элементті терулері үшеу: {а, в}, {а, с}, {в, с}.
п -
элементтен
к -
элемент бойынша терулер саны
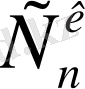 арқылы белгіленеді және келесі тендік орындалады
арқылы белгіленеді және келесі тендік орындалады
(4)
▼
А
к
п
санын келесі тәсілмен алуға болады: алдымен
п
элементтен
к -
элемент бойынша терулерді аламыз (олардың саны -
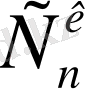 ), содан соң алынған әрбір
к -
элементті теруге алмастырулар жасалады (олардың саны - к
!
) . Онда,
), содан соң алынған әрбір
к -
элементті теруге алмастырулар жасалады (олардың саны - к
!
) . Онда,
А
к
п
=
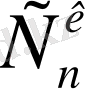 . к!, ал бұдан
. к!, ал бұдан
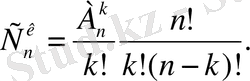
Мысал. Жиналыстағы 30 кісіден конференцияға екі делегатты қанша тәсілмен сайлауға болады?
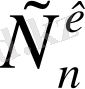 санының кейбір қасиеттері:
санының кейбір қасиеттері:
1)
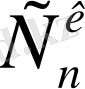 =
=
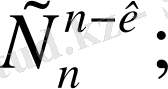
2)
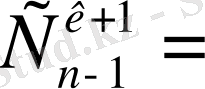
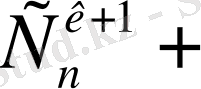
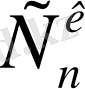 , k<n
, k<n
3)
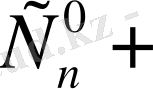
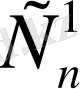 +
+
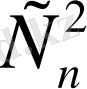 +…+
+…+
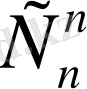 =2
n
=2
n
1)
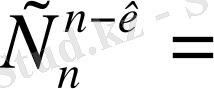
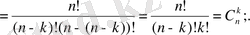
2)
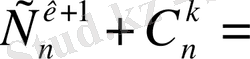

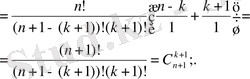
3) қасиетті математикалык индукция әдісімен дәлелдеуді оқырманға тапсырамыз.
Ескерту. 3) қасиетті Ньютон формуласынан да алуға болады (келесі пунктті қараңыз) .
3. Ньютон формуласы. Жоғарыдағы 2) қасиеттен "Паскаль үшбұрышы" деп аталатын келесі кестені алуға болады
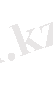
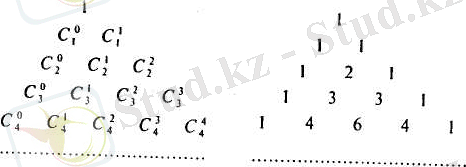
Кестенің басында және әрбір жолдың ұштарында 1 саны тұр; ал әрбір жолдың кез келген орнындағы (ұштарынан басқа) сан, үстіндегі алдыңғы жолдағы екі санның қосындысына тең. Паскаль үшбұрышы - (а + в) " түріндегі бином дәрежесінің Ньютон формуласы бойынша жіктелуіндегі биномдық коэффициенттердің мәндерін береді.
Назарыңызға! "Паскаль үшбұрышы" атауы тарихи дұрыс емес. Мұндай үшбұрыштарды XIII ғ. араб математиктері Гиясэддин Каши мен Омар Хайям қолданған. Ал Блэз Паскаль (1623-1662) жж. өмір сүрген.
Ньютон формуласы келесі түрде жазылады:
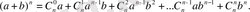 (Н. ф. )
(Н. ф. )
Бұл теңдікті математикалық индукция әдісімен дәлелдеуге болады. Мұндағы
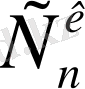 сандарын кейде
биномдық коэффициенттер
деп атайды.
сандарын кейде
биномдық коэффициенттер
деп атайды.
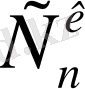 сандары - Ньютон формуласының
к-
мүшесінің коэффициенттері, ал
к-
мүше
сандары - Ньютон формуласының
к-
мүшесінің коэффициенттері, ал
к-
мүше
Т
к
=
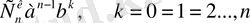 арқылы белгіленеді.
арқылы белгіленеді.
Егер Ньютон формуласында а = b=1 деп алсақ, онда жоғарыдағы 3) қасиеттің дұрыс екенін көреміз:
2 n = (1 +1) n =
(4)
Бұл теңдік, п элементті жиынның барлық ішжиындарының саны 2 n тең болатынын көрсетеді.
Назарыңызға! Ньютон формуласы атауы тарихи дұрыс емес. Ол Ньютонға дейін жоғарыда аталған XIII ғ. араб математигі Гиясэддин Кашиге белгілі болған.
1-мысал.
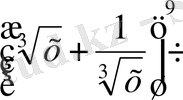 көпмүшелігінің төртінші мүшесін табу керек.
көпмүшелігінің төртінші мүшесін табу керек.
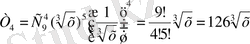
2-мысал.
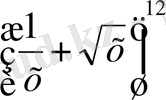 - көпмүшелігінің
х-ке
тәуелсіз
мүшесін табу керек.
- көпмүшелігінің
х-ке
тәуелсіз
мүшесін табу керек.
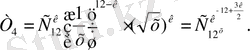 Бұл
мүше
х-ке
тәуелсіз
болуы үшін
Бұл
мүше
х-ке
тәуелсіз
болуы үшін
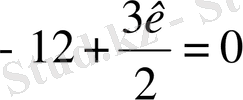 болуы керек.
Олай
болса,
к
= 8.
болуы керек.
Олай
болса,
к
= 8.
Сонымен,
3-мысал. Үлкен бөлмені жарықтандыруға ондағы 10 электр шамының әрбіреуін қосуға болады. Бөлмені қанша тәсілмен жарықтандыруға болады?
▼ 10 элементті жиынның барлық ішжиындары қанша болса, сонша тәсіл бар, яғни 2 10 = 1024. Мұнда электр шамының бірде-бірі жанбауы да қосылып тұр.
ФУНКЦИЯЛАРДЫҢ ҚАСИЕТТЕРІ
Функция түсінігі
Егер Х жиынының әрбір х (тәуелсіз айнымал) элементіне қандай да бір f ережесі (заңы) бойынша жалғыз у (тәуелді айнымал) элементі сәйкес келсе, онда анықталу аймағы X жиыны болатын у = f ( х) функциясы берілді немесе Х жиынында у = f(х) функциясы берілді дейді. Осымен бірге, барлық у элементтерінен құралған У жиынын у = f (х) функциясының өзгеру аймағы деп атайды (бізде X пен Ү - тек сандар жиыны болады) .
Егер осы анықтамадағы ереже формула арқылы көрсетілсе, онда функңия аналитикалық тәсілмен берілді дейді.
Мысалдар:
1. п қандай да бір натурал сан болсын. Онда әрбір х нақты санына жалғыз х" нақты санын сәйкестендіруге болады. Олай болса, анықталу аймағы барлық нақты сандар жиыны болатын у-х n функциясы берілді;
2.
у=х
2
,
1
 х
х
 3 функциясын қарастырайық. Бұл жазу [1; 3] кесіндісінен алынған әрбір
х
санына осы санның квадраты сәйкестендірілетін функция берілгенін көрсетеді:
f (1)
=1
2
= 1,
f
(2) =
2
2
=4, f [2, 3)
2
=
5, 29 . . . Бірақ,
f
(4) -тің мағынасы жоқ, өйткені 4
3 функциясын қарастырайық. Бұл жазу [1; 3] кесіндісінен алынған әрбір
х
санына осы санның квадраты сәйкестендірілетін функция берілгенін көрсетеді:
f (1)
=1
2
= 1,
f
(2) =
2
2
=4, f [2, 3)
2
=
5, 29 . . . Бірақ,
f
(4) -тің мағынасы жоқ, өйткені 4
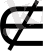 [1; 3], яғни 4 саны функцияның анықталу аймағында жоқ;
[1; 3], яғни 4 саны функцияның анықталу аймағында жоқ;
3. Кез-келген х нақты саны үшін: "х рационал сан болса, онда у = 1; х иррационал сан болса, онда у = 0" деген ережемен анықталған функцияны Дирихле функциясы деп атайды. Оны қысқаша былай жазады

4. Кез-келген х нақты сан үшін: "егер де оң сан болса, онда у = 1; егер х теріс сан болса, онда у = - 1; егер де = 0 болса, онда у = 0", - деген ережемен анықталған функцияны х-тің таңбасы деп атайды да, y=signx деп белгілейді. Оны қысқаша былай жазады
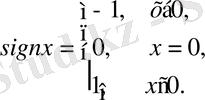
(signx - „сигнум х" деп оқылады; лат, signum-таңба) ;
5. Кез-келген нақты саны үшін:
егер
п
натурал, ал 0
 a <
1 болатын сандар болып, х =
п
+ а
болса, онда
у
= n;
a <
1 болатын сандар болып, х =
п
+ а
болса, онда
у
= n;
егер m натурал, ал 0
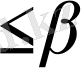 < 1 болатын сандар болып
х=-т+
< 1 болатын сандар болып
х=-т+
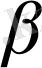 болса, онда
у
= - т;
болса, онда
у
= - т;
егер
0
 х<
1 болса, онда
у
=
0,
- деген ережемен анықталған функция
х-тің бүтін бөлігі
деп аталады да қысқаша у=[x] арқылы белгіленеді.
у =[х]
функциясын былайша анықтауға болады:
[х]
арқылы х-тен үлкен емес ең үлкен бүтін caн белгіленеді;
х<
1 болса, онда
у
=
0,
- деген ережемен анықталған функция
х-тің бүтін бөлігі
деп аталады да қысқаша у=[x] арқылы белгіленеді.
у =[х]
функциясын былайша анықтауға болады:
[х]
арқылы х-тен үлкен емес ең үлкен бүтін caн белгіленеді;
6) функциясының анықталу және өзгеру аймақтарын табу керек.
Шешуі:
Квадрат түбір анықтамасы бойынша
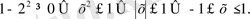 Яғни функцияның анықталу аймағы х=[-1; 1] . Функцияның өзгеру аймағы, 1-х
2
айырмасының ең кіші мәні мен ең үлкен мәніне, ал өз кезегінде 1 - х
2
айырмасының ең кіші мәні мен ең үлкен мәні-азайтқыш х
2
-тың ең үлкен мәні мен ең кіші мәніне тікелей байланысты. Анықталу аймағын ескере отырып 0
Яғни функцияның анықталу аймағы х=[-1; 1] . Функцияның өзгеру аймағы, 1-х
2
айырмасының ең кіші мәні мен ең үлкен мәніне, ал өз кезегінде 1 - х
2
айырмасының ең кіші мәні мен ең үлкен мәні-азайтқыш х
2
-тың ең үлкен мәні мен ең кіші мәніне тікелей байланысты. Анықталу аймағын ескере отырып 0
 х
г
<
1 қос теңсіздігін жаза аламыз. Бұдан
х
г
<
1 қос теңсіздігін жаза аламыз. Бұдан
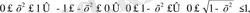
яғни функцияның өзгеру аймағы Y= [0; 1] шығады;
7)
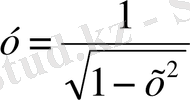 функциясының
анықталу
аймағын және
өзгеру
аймағын табу керек.
функциясының
анықталу
аймағын және
өзгеру
аймағын табу керек.
Шешуі.
Квадрат түбір анықтамасы бойынша 1-х
2
 0. Сонымен бірге бөлшектің бөлімі нөлге тең емес болуы керек:
0. Сонымен бірге бөлшектің бөлімі нөлге тең емес болуы керек:
1 - х
2
 0 Бұл
екі
шарттың екеуі де орындалуы үшін 1-х
2
> 0 <=> х
2
< 1 <=> /х/ < 1 <=> -1 < х < 1 орындалуы керек, яғни функцияның анықталу аймағы
Х=
(-1; 1) . Функциянын өзгеру аймағы бөлшектің бөлімінің қабылдайтын мәндеріне тәуелді. Ал 1 - х
2
айырымының ең үлкен мәні азайтқыш х
2
-тың ең кіші мәніне х
2
=0 сәйкес келетінін қору қиын емес. Олай болса, бөлшектің бөлімінің, яғни 1 -
х
2
айырымының ең үлкен мәні 1-ге тең. Сондықтан бөлшектің ең кіші мәні
0 Бұл
екі
шарттың екеуі де орындалуы үшін 1-х
2
> 0 <=> х
2
< 1 <=> /х/ < 1 <=> -1 < х < 1 орындалуы керек, яғни функцияның анықталу аймағы
Х=
(-1; 1) . Функциянын өзгеру аймағы бөлшектің бөлімінің қабылдайтын мәндеріне тәуелді. Ал 1 - х
2
айырымының ең үлкен мәні азайтқыш х
2
-тың ең кіші мәніне х
2
=0 сәйкес келетінін қору қиын емес. Олай болса, бөлшектің бөлімінің, яғни 1 -
х
2
айырымының ең үлкен мәні 1-ге тең. Сондықтан бөлшектің ең кіші мәні
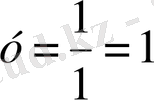 тең. Ал х айнымал 1-ге ұмтылғанда 1
-х
2
айырымы нолге ұмтылады да бөлшектің өзі (1 - х
2
>
0 болғандықтан) +
тең. Ал х айнымал 1-ге ұмтылғанда 1
-х
2
айырымы нолге ұмтылады да бөлшектің өзі (1 - х
2
>
0 болғандықтан) +
 - қа ұмтылады. Сонымен функцияның өзгеру аймағы Y=[1; +
- қа ұмтылады. Сонымен функцияның өзгеру аймағы Y=[1; +
 ) .
) .
Жазықтықтағы тік бұрышты координаталар жүйесі
Қарапайым және жиірек қолданылатын тік бұрышты координаталар жүйесін қарастырамыз.
Өзара перпеидикуляр екі түзу берілсін. Түзулердің қиылысу нүктесін санау басы немесе координнаталар басы деп есептейміз. Әрбір түзуге оң бағыт береміз (анықтаймыз) және координаталар басынан бастап оң бағытта осы түзулерге бірлік кесіндіні саламыз. Бұл түзулерді координата түзулері немесе координата остері деп атайды және олардың біреуін абсцисса өсі, ал екіншісін - ордината өсі деп атау қабылданған. Координаталар басын О, абсциссалар осін ОХ, ал ординаталар өсін ОY әріптерімен белгілейміз. Көбінесе абсциссалар өсі жатық (горизонталь) және оның он жарты өсі оңға қарай бағытталатындай етіп орналастырылады (мұндай координаталар жүйесін оң бағытталған дейді, 1-сурет) .
Жазықтықтың кез келгеи М нүктесін алайық. М нүктесі арқылы координаталар өстеріне параллель түзулер жүргіземіз. ОҮ ө сіне параллель түзу абсциссалар осін N нүктесінде, ал ОХ өсіне параллель түзу ординаталар өсін L нүктесінде қияды. N нүктесінің абсциссалар өсіндегі координатасы "b", L нүктесінің ординаталар өсіндегі координатасы " b " болады. Онда М нүктесініц ОХУ коордииаталар жүйесіндегі координаталары деп, реттелген қос (а, b) сандарын айтады. а саны М нүктесінің бірінші координатасы немесе абсциссасы, b саны М нүктесінің екінші координатасы немссе ординатасы
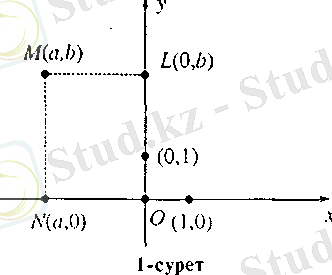 деп аталады да және
М (а, b)
деп жазылады (мұнда алдымен абсцисса, содан соң ордината жазылатынына, яғни
a
мен
b
сандарының орна-ласу ретіне назар аудару керек) .
деп аталады да және
М (а, b)
деп жазылады (мұнда алдымен абсцисса, содан соң ордината жазылатынына, яғни
a
мен
b
сандарының орна-ласу ретіне назар аудару керек) .
Координаталық тузу - барлық нақты сандар жиынының геометриялық моделі болатыны сияқты, барлық қос нақты сандар жиынының геометриялық моделі - координаталар жазықтығы.
Функцияның графигі
У - f(x) функциясы берілсін. Егер абсциссасы функцияның анықталу аймағында жататын, ал ординатасы функцияның сәйкес мәніне тең болатын барлық нүктелерді координаталар жазықтығында белгілесек, онда (x; f(x) ) нүктелерінің жиыны функцияның графигі болады.
Мысал: у=х 2 функциясының графигін салу керек.
Шешуі: Функцияның кейбір мәндерінің кестесін құрамыз:
2-кесте
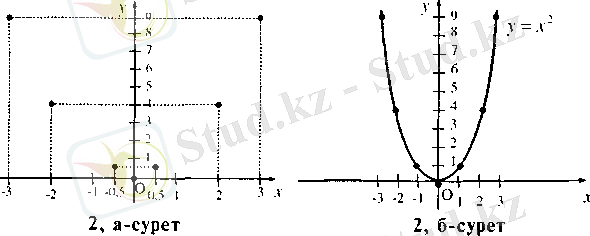
Табылған (0; 0), (0, 5; 0, 25), (1; 1), (2; 4), (2, 5; 6, 25), (-0, 5; 0, 25), (-1; 1), (-2; 4), (-2, 5; 6, 25) нүктелерін координаталар жазықтығына түсіреміз (2, а-сурет) . Бұл нүктелерді тегіс тұтас сызықпен қосып функциясынын графигін (дәлірегі, графиктің эскизін (нобайын) ) аламыз (2, 6-сурст) . Бұл сызықты парабола деп атайды.
Жұп және тақ функциялар
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz