Кванторы бар сөйлемдерді теріске шығару ережелері

Жоспар
Кіріспе

ІІ.9. Кванторы бар сөйлемдерді теріске шығару ережелері
11.11. Тең жиындар. Бос жиын. Ішкі жиын, оның тұрлері. Универсал әмбебап жиын
П.12. Жиындардың қиылысуы және оның қасиеттері
П. 13. Жиындардың бірігуі және оның қасиеттері
ІІ.14. Жиындардың айырымы. Толықтауыш жиын
17. 15. Жиындардың декарттық көбейтіндісі
17. 16. Жиындарды өзара қиылыспайтын ішкі жиындарға бөліктеу ұғымы
П. 17. Жиындардың декарттың көбейтіндісін координаттың жазықтықта кескіндеу
§4. Қатыстар және сәйкестіктер
ІІ.18. Қатыс ұғымы. Қатыстыц берілу тәсілдері
П. 19. Қатыстың қасиеттері
П.20. Эквивалент қатысы
П.21. Реттік қатыс
П. 22. Сәйкестік ұғымы. Сәйкестіктің графы,
графигі
П.23. Берілген сәйкестікке кері сәйкестік
11.24. Өзара бір мәнді сәйкестіктер
ІІ.25. Тең қуатты жиындар
§5. Тақырыптық есептер экәне оларды шешу
П.26. Тақырыптың есеп ұғымы
ІІ.27. Есепті шешу тәсілдері

Жалпы, сөйлемді теріске шығару дегеніміз - берілген сөйлемнің мағынасы шын болса, оны жалған етіп өзгерту немесе керісінше жалған болса, мағынасын шын етіп өзгерту.
Мысалы:
1. А: 23 саны тақ сан - Ш
¬ А: 23 саны сақ сан емес – Ж
2. А: 257 саны үш таңбалы сан - Ш
¬ А:257 саны үш таңбалы емес - Ж
З. А:4+3 = 8-Ж
¬ А: 4+3≠8 - Ш
Бұл сөйлемдердің құрамында кванторлар жоқ. Егер сөйлемдердің құрамында кванторлар болса, онда мұндай сойлемдерді қалайша теріске шығаруға болады?
Алдымен жалпылау кванторы бар сөйлемдерді қарастырайық:
А: «Барлық натурал сандар 3-ке бөлінеді» - Ж.
Бұл сөйлемді мынадай екі жолмен теріске шығаруға болады:
1. ¬ А: Барлың натурал сандардың 3-ке бөлінетіні дұрыс емес - Ш.
2. ¬ А: Кейбір натурал сандар 3-ке бөлінбейді - Ш.
Берілген сөйлемді «Барлық натурал сандар 3-ке бөлінбейді», - деп теріске шығаруға болмайды. Өйткені бұл сөйлемнің де мағынасы жалған. Сонымен, жалпылау кванторы бар сөйлемдерді теріске шығару үшін:
1. Сөйлемнің соңына «дұрыс емес» сөзін қосамыз.
2. Жалпылау кванторын бар болу кванторымен алмастырып, соңғы сөздің терістемесін аламыз.
Енді бар болу кванторы бар сөйлемдерді теріске шығару жолдарын қарастырайық:
А: «Кейбір тақ сандар 4-ке бөлінеді» - Ж.
Бұл сөйлемді мынадай екі жолмен теріске шырауға болады:
1. ¬ А: «Кейбір тақ сандардың 4-ке бөлінетіні дұрыс емес» - Ш.
2. ¬ А: «Барлың тақ сандар 4-ке бөлінбейді» - Ш.
Берілген сейлемді «Кейбір таң сандар 4-ке бөлінбейді», - деп теріске шығаруға болмайды, өйткені бұл сөйлем де мағынасы жағынан алған. Сонымен, бар болу кванторы бар сөйлемдерді теріске шығару үшін:
1. Сөйлемнің соңына дұрыс емес сөзін қосамыз.
2. кванторын жалпылау кванторымен алмастырып, соңғы сөздің терістемесін аламыз.

элементтерін латынның кіші әріптерімен белгілейді: а,b, с, d ,...
Математикада және ғылымның басқа да салаларында қандай бір объектінің қарастырылып отырылған жиынға тиісті немесе тиісті емес екендігін анықтауға тура келетін жағдайлар жиі кездеседі. Мысалы, 7 саны натурал сан. Басқаша айтқанда 7 саны натурал сандар жиынына тиісті деп айтуға болады. Жалпы, «а объектісі А жиынына тиісті» - деген сөйлемді арнайы белгінің көмегімен былай жазуға болады: а € А. Бұл сөйлемді тұрліше оқиды:
- а объектісі А жиынына тиісті.
- а объектісі А жиынының элементі.
- А жиынында а элементі бар.

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 44 бет
Таңдаулыға:

ІІ.9. Кванторы бар сөйлемдерді теріске шығару ережелері
Жалпы, сөйлемді теріске шығару дегеніміз - берілген сөйлемнің мағынасы шын болса, оны жалған етіп өзгерту немесе керісінше жалған болса, мағынасын шын етіп өзгерту.
Мысалы:
1. А: 23 саны тақ сан - Ш
- А: 23 саны сақ сан емес - Ж
2. А: 257 саны үш таңбалы сан - Ш
- А:257 саны үш таңбалы емес - Ж
З. А:4+3 = 8-Ж
- А: 4+3!=8 - Ш
Бұл сөйлемдердің құрамында кванторлар жоқ. Егер сөйлемдердің құрамында кванторлар болса, онда мұндай сойлемдерді қалайша теріске шығаруға болады?
Алдымен жалпылау кванторы бар сөйлемдерді қарастырайық:
А: Барлық натурал сандар 3-ке бөлінеді - Ж.
Бұл сөйлемді мынадай екі жолмен теріске шығаруға болады:
1. - А: Барлың натурал сандардың 3-ке бөлінетіні дұрыс емес - Ш.
2. - А: Кейбір натурал сандар 3-ке бөлінбейді - Ш.
Берілген сөйлемді Барлық натурал сандар 3-ке бөлінбейді, - деп теріске шығаруға болмайды. Өйткені бұл сөйлемнің де мағынасы жалған. Сонымен, жалпылау кванторы бар сөйлемдерді теріске шығару үшін:
Сөйлемнің соңына дұрыс емес сөзін қосамыз.
Жалпылау кванторын бар болу кванторымен алмастырып, соңғы сөздің терістемесін аламыз.
Енді бар болу кванторы бар сөйлемдерді теріске шығару жолдарын қарастырайық:
А: Кейбір тақ сандар 4-ке бөлінеді - Ж.
Бұл сөйлемді мынадай екі жолмен теріске шырауға болады:
1. - А: Кейбір тақ сандардың 4-ке бөлінетіні дұрыс емес - Ш.
2. - А: Барлың тақ сандар 4-ке бөлінбейді - Ш.
Берілген сейлемді Кейбір таң сандар 4-ке бөлінбейді, - деп теріске шығаруға болмайды, өйткені бұл сөйлем де мағынасы жағынан алған. Сонымен, бар болу кванторы бар сөйлемдерді теріске шығару үшін:
Сөйлемнің соңына дұрыс емес сөзін қосамыз.
кванторын жалпылау кванторымен алмастырып, соңғы сөздің терістемесін аламыз.

элементтерін латынның кіші әріптерімен белгілейді: а,b, с, d ,...
Математикада және ғылымның басқа да салаларында қандай бір объектінің қарастырылып отырылған жиынға тиісті немесе тиісті емес екендігін анықтауға тура келетін жағдайлар жиі кездеседі. Мысалы, 7 саны натурал сан. Басқаша айтқанда 7 саны натурал сандар жиынына тиісті деп айтуға болады. Жалпы, а объектісі А жиынына тиісті - деген сөйлемді арнайы белгінің көмегімен былай жазуға болады: а Euro А. Бұл сөйлемді тұрліше оқиды:
а объектісі А жиынына тиісті.
а объектісі А жиынының элементі.
А жиынында а элементі бар.
А жиыны а элементін қамтиды. а объектісі А жиынына тиісті емес - деген сөйлемді а Euro А тұрінде жазамыз. Бұл сөйлем былай оқылады:
а объектісі А жиынына тиісті емес.
а объектісі А жиынының элементі емес.
А жиынына а элементі жатпайды.
Жиынды және оның элементін былай жазу келісілген. Мысалы, А - жиыны белгісінен кейін теңдік белгісін қойып, фигуралы жақшаның ішіне жиын элементтерін жазамыз: А={а, Ь, с, 6}.
Жиын элементі жиынға бір рет қана тиісті болады. Жиын элементтерінің саны шектеулі және шектеусіз болады. Мысалы, ай күндерінің саны, сыныптағы оқушылар саны, т.б. шектеулі, ал түзудің бойындағы нүктелер саны шектеусіз. Сондай-ақ сан жиындары -натурал, бүтін, рационал, нақты сандар жиындарының элементтерінің саны өте көп, шектеусіз. Бұл жиындарды мынадай әріптермен белгілейміз:
А
N- натурал сандар жиыны;
Z -- бүтін сандар жиыны; л \
Q - рационал сандар жиыны;
R - нақты сандар жиыны.

Жиынды схема тұрінде белгілеу үшін, түйықталған контурды пайдаланамыз. Оны Эйлер-Венн диаграммасы деп атайды.
Леонард Эйлер (1703-1783) - Петербург ғылым академиясының мүшесі, Швейцарияда туған, ал 1727 жылы Петербург Ғылым академиясының шақыруымен Ресейге келген және мұнда ірі математик дәрежесіне дейін көтерілген. Джон-Венн (1834-1923) ағылшын математигі.
Жиын ұғымын біз анықтамасыз қолданатынымыз туралы айтқан болатынбыз. Қандай да бір заттар тобы жиын бола ала ма, жоқ па, оны қалай білуге болады?
Егер әрбір объект туралы, оның жиынға тиісті немесе тиісті емес екендігі туралы айта алатын болсақ, онда жиын берілген деп есептелёді (саналады), яғни жиын өзінің элементтері арқылы анықталады. Жиынның берілуінің мынадай негізгі екі тәсілі бар:
1. Жиынды оның барлық элементтерін жазып көрсету арқылы беру. Мысалы, А жиыны 1-ден б-ға дейінгі сандар болсын. Бұл жағдайда жиынды былай жазып көрсетуге болады:
А=

А={1,2,3,4,5,6}
Кейбір жағдайда жиын элементтері шектеусіз (шексіз) көп болуы мүмкін. Мұндай жағдайда жиын элементтерінің барлығын жазып көрсету арқылы беру мүмкін емес. Бұл жағдайда жиын элементтерінің характеристикалық (сипаттамалық) қасиеттерін көрсету арқылы беруге болады.
Сонымен жиынның берілуінің 2-ші тәсілі:
2. Жиынға тиісті элементтердің бәріне ортақ сипаттамалық қасиеттерін көрсету арқылы беру. Мысалы, В- 6-дан артық барлық натурал сандар жиыны болсын. Бұл жиынның барлық элементтерін жазып көрсету мүмкін емес. Сондықтан бұл жиынды мынадай тұрде жазып көрсетуге болады:
В=
={хх
еЫ,

В={ххEuroN,х6}
Жиыидарды берудің 2-ші тәсілі жалпылама тұрде алынған. Бұл тәсіл арңылы элементтері шектеулі және шектеусіз жиындарды беруге болады.
Бастауыш курс математикасында жиын ұғымы және жиын элементтері айқын тұрде берілмейді. Дегенмен, олар бастауыш курс математикасының өн бойында қолданылады.
Тексеру сұрақтары:
Жиын сөзінің мағынасын қалай түсінесің? Жиынға мысалдар келтір.
Жиындарды қалай белгілейді?
Жиын элементі дегеніміз не?
Жиын элементтерін қалай белгілейді? Жиынға және оның элементтеріне мысал келтір.
Жиынды және оның элементтерін қалай жазады?
Жиынды схема тұрінде қалай белгілейміз?
Жиынды берудің қандай тәсілдерін білесің?
Жиынды берудің 1-ші тәсілінің мәнін түсіндір.
Жиынды берудің 2-ші тәсілінің мәнін түсіндір.

11.11. Тең жиындар. Бос жиын. Ішкі жиын, оның тұрлері. Универсал әмбебап жиын
Анықтама: Егер А және В жиындары бірдей элементтерден тұратын болса, онда мұндай жиындарды тең жиындар деп атайды және былай белгілейді: А=В
Мысал:А={2,4,6,8},В={6,4,2,8}.Көріп отырғанымыздай, А және В жиындары бірдей элементтерден тұрады. Ендеше А=В.
Ескерту: Жиындардың теңдігін анықтағанда элементтердің орналасу реті есепке алынбайды.
Анықтама: Бірде-бір элементі жоқ жиынды бос жиын деп атайды және оны былай белгілейді: Ø.
Ескерту: Бос жиынның белгісі фигуралы жақшаға алынбайды. Мысалы, А = Ø тұрінде жазылады.
Мысал:А={11,12,13,14,15}жиыны берілсін. Осы жиын элементтерінің ішінен бір таңбалы сандарды теріп жазу керек болсын. Ол жиынды В деп белгілесек, онда В жиынына тиісті болатын элементтер жоқ. Ендеше, В = Ø
Анықтама: Егер В жиынының әрбір элементі А жиынына тиісті болса, онда В жиыны А жиынының ішкі жиыны деп аталады және былай белгіленеді.
Мысал:А={1,2,3,4,5,6,7,8},В={1,3,5, 7}В жиынының әрбір элементі А жиыны элементтерінің ішінде бар.
А
В жиыны А жиынына ішкі жиын екендігін Эйлер дөңгелектері арқылы былай керсетуге болады:

В

Ішкі жиынды меншікті ішкі жиын және меншікті емес ішкі жиын деп екіге бөледі. Берілген А жиыиымен дәлме-дәл келмейтін, яғни А жиынына тең болмайтын ішкі жиындарды меншікті ішкі жиын деп атайды.
Мысал: А={1,3,5} жиынының меншікті ішкі жиындарын бөліп алу керек болсын. Сонда: Ах={1}, А2={3}, А3={5}, А4={1,3}, А5={1,5}, А6={3,5}.
Сонымен берілген А жиынының алты меншікті ішкі жиыны бар екен. Бұл ішкі жиындардың бірде-біреуі А жиынымен дәлме-дәл келмейді, яғни А жиынына тең емес.
Кез келген жиынның екі меншікті емес ішкі жиыны болады. Олар: берілген жиынның өзі және бос жиын. Сонымен, кез келген жиын өзіне-өзі меншікті емес ішкі жиын болады. Сол сияқты бос жиын да кез келген жиынға меишікті емес ішкі жиын бола алады.
Математикада оқытылатын объектілердің жиынын үлкенірек жиынның ішкі жиыны ретінде қарастыратын жағдай жиі кездеседі. Осындай жиын әмбебап жиын деп аталады.
Мысалы, А1 - педколледждегі бастауыш мектеп бөлімінің I курс студенттерінің жиыны, А2 - бастауыш мектеп бөліміндегі барлың студенттер жиыны, ал А3 педколледждегі барлың студеиттер жиыны болсын. Бұл жағдайда А3 жиыны Ах және А2 жиындары үшін әмбебап жиын болып есептеледі, яғни олардың әрңайсысы А3 жиынының ішкі жиындары.
Әмбебап жиынды әдетте U әрпімен белгілейді. Оны схемада тік төртбұрыш тұрінде, ал оның ішкі жиындарын Эйлер дөңгелектерімен белгілейді. Осыны пайдаланып жоғарыда қарастырылған мысалды мынадай тұрде көрсетуге болады:

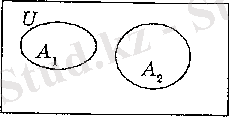
Тексеру сұрақтары:
Тең жиындар деп қандай жиындарды айтады? Мысал келтір.
Бос жиын деп қандай жиынды айтады? Оны қалай белгілейді? Мысал келтір.
Ішкі жиын деп қандай жиынды айтады? Белгісін көрсет. Мысал келтір.
Ішкі жиынның қандай турлерін білесің?
Меншікті ішкі жиын деп қандай ішкі жиынды айтады? Мысал келтір.
Меншікті емес ішкі жиын деп қандай ішкі жиынды айтады? Мысал келтір.
7. Универсал жиын деп қандай жиынды айтады және
оны қалай белгілейді? Мысал келтір.

П.12. Жиындардың қиылысуы және оның қасиеттері
А={2,4,6,8} және В={5,6,7,8,9} жиындары берілсін. Осы жиындардың екеуіне де тиісті ортақ элементтер-ден тұратын жаңа С жиынык құрайық: С={6,8}. Алынған С жиынын А және В жиындарының қиылысуы деп атайды.
Анықтама: А және В жиындарыиың қиылысуы деп А және В жиындарының екеуіне де тиісті ортақ элементтерден тұратын жиынды айтады.
А және В жиындарының қиылысуын былай белгілейді: А∩В∩-қиылысу белгісі. А және В жиындары қиылысу белгісі. Ажәне В жиындарының қиылысуын Эйлер-Венн диаграммасы арқылы бейнелейтін болсаң, онда бұл жиындардың қиылысуы суретте штрихталған (боялған) бөлік болады.

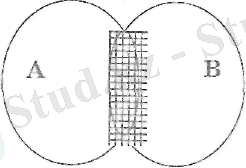
Ескерту: Егер жиындардың ортақ элементтері болмаса, онда олардың қиылысуы бос жиынға тең.
Мысал: А={1,3,5,7,9}, В={2,4,6,8}. А∩В.
Жиындардың қиылысуы үшін бірқатар қасиеттер орындалады.
1° Кез келген А жөне В жиындары үшін қиылысудың коммутативті (орын ауыстырымдылық) заңы орындалады: А∩В = В∩А.
Мысал: А={а,Ь,с,d,е}, В={Ъ, е, f}. А∩В={b, е}, ал В∩А={b, е}. Ендеше, А∩В=В∩А.
2°. Кез келген А, В жөне С жиындары үшін қиылысудың ассоциативті (терімділік) заңы орындалады: (А∩ (В∩ А)= (А∩ (В∩С).
Бұл қасиетті Эйлер-Венн диаграммасының к-мегімен дәлелдеуге болады:

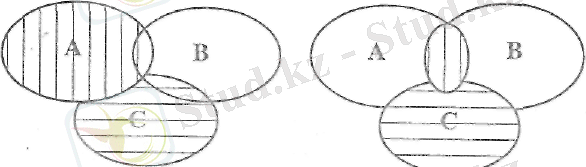
Суретте теңдіктің сол жақ жәyе оң жақ бөліктері көрсетілген. а) Суретте тік сызықпен В∩С жиыны шрихталған. Екі рет штрихталған белік А∩(В∩С) жиынын бейнелейді. ә) Суретте вертикаль сызықпен А∩В жиыны, горизонталь сызықпен С жиыны бейнеленген. Екі рет штрихталған бөлікте (А∩В) ∩С жиыны бейнеленген. Диаграммаларды салыстыра отырып, А∩(В∩С)=(А∩В) ∩С деген қорытынды жасауға болады. Өйткені диаграмманың екеуінде де бірдей бөлік екі рет штрихталған.
3°. Егер ВcА болса, онда А∩В=В.
Мысал:А={1,2,3,4,5,6},В={2,4,6}мұнд ағы ВсА екені көрініп тұр. Жиындардың қиылысуын табамыз. А∩В={2,4,6}. Қиылысудан шықңан жиын мен В жиынының элементтерін салыстырсаң, онда бұл екеуінің элементтері бірдей екендігін байқаймыз. Ендеше, А∩В=В мұндағы ВсА.
4°. Кез келген жиын мен Ø жиынның қиылысуы бос жиынға тең және кез келген жиынның өзіне-өзі қиылысуы сол жиынның өзіне тең, яғни: А∩Ø=Ø жөне А∩А=А. Жиындардың қиылысуы 2х6 тұріндегі теңсіздіктерді шешкенде қолданылады.

х=2 және х=6 теңсіздіктері шешімдерінің қиылысуы штрихталған бөлік болып табылады.
Бастауыш курс математикасында қарастырылатын көбейтудің заңдары және көбейтудің ерекше жағдайлары жиындардың қиылысу амалының қасиеттеріне негізделеді.
Тексеру сұрақтары:
Жиындардың қиылысуын анықта. Мысал келтір.
Жиындардың қиылысуын Эйлер-Венн диаграммасы арқылы кескінде.
Қиылысудың қандай қасиеттерін білесің?
2-ші қасиетті Эйлер-Венн диаграммасының көмегімен дәлелде.

П. 13. Жиындардың бірігуі және оның қасиеттері
А={1,2,3,4,5}, В={6,7,8} жиындары берілсін. Осы жиындардың ең болмағанда біреуіне тиісті болатын бар-лың элементтерден тұратын жаңа С жиынын құрайық:
С={1,2,3,4,5,6,7,8}. Алынған С жиынын А және В жиындарының бірігуі деп атайды.
Акықтама: А және В жиындарының бірігуі деп А және В жиындарының ең болмағанда біреуіне тиісті болатын барлық элементтерден тұратын жиынды айтады.
А және В жиындарының бірігуін былай белгілейді: АUВ. U- бірігу белгісі А және В жиындарының бірігуін Эйлер-Венн диаграммасы арқылы бейнөлейтін болсақ, онда олардың бірігуі штрихталған бәлік болады.

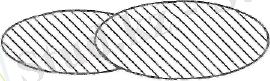
Жиындардың екеуіне де тиісті ортақ элементтер бірігуде тек бір рет қана жазылады. Мұны диаграммадан да көруге болады. Диаграммада қиылысып тұрған бөлік бір рет қана штрихталған. Осы айтылғанды мысалмен көрсетейік.
Мысал:А={11,12ДЗ,14,15},В={14,15,16 ,17}.
АUВ={11,12,1ЗД4,15,16,17}. Мұнда 14 және 15 сандары А және В жиындарының екеуіне де тиісті. Бірақ бірігуде бұл элементтер тек бір рет қана жазылып тұр.
Жиындардың бірігуі үшін бірқатар қасиеттер орындалады:
1°. Кез келген А және В жиындары үшін бірігудің коммутативті (орын ауыстырымдылық) заңы орындалады, яғни АUВ=ВUА.
2°. Кез келген А, В және С жиындары үшін бірігудің ассоциативті (терімділік) заңы орындалады, яғни АU (ВUС) = (АUВ) UС. Бұл қасиет үш және одан да көп жиындардың бірігуін табуға мүмкіндік береді.
3°. Егер ВсА, онда АUВ=А. Мысал:
А={1,2,3,4,5,6,7,8,9,10}
В={1,3,5,7,9}. Мұндағы ВсА. АUВ={1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Ендеше, АUВ=А.
4°. Кез келген жиын мен бос жиынның бірігуі сол жиынның өзін береді, яғни АUØ=А.
5°. Кез келген А, В және С жиындары үшін бірігу мен қиылысудың бір-біріне қатысты дистрибутивті (үлестірімділік) заңы орындалады.
а) (АUВ)∩С=(А∩С) U (В∩С)
ә) (А∩В) UС=(АUС)∩(ВUС)
Ескерту: Егер жақшасыз өрнекте қиылысу мен бірігу амалдары араласып келетін болса, онда алдымен қиылы-су амалы орындалады.
Бастауыш сыныпта қарастырылатын қосу амалы және оның заңдары жиындарды біріктіру амалына және бірігудің қасиеттеріне негізделеді. Сөзіміз дәлелді болу үшін бастауыш сыныпта шығарылатын мынадай мысалды талдап көрейік.
Оқушыларға 4+3=7 екеыін түсіидіру үшін мүғалім оқушыларға 4 қызыл дөңгелек жөне 3 кәк дөңгелек алуды ұсынады да, қызыл дөңгелектерге кек дөңгелектерді жақындату керек екендігін айтады. Осыдан кейін оқушылар барлық дөңгелектер санын санап, барлығы 7 болғандығына көздерін жеткізеді. Мұнда біз іс жүзінде екі жиын элементтерін, яғни қызыл дөңгелектер мен көк дөңгелектер жиынын біріктірдік.
Тексеру сұрақтары:
Жиындардың бірігуінің анықтамасы қалай тұжырымдалады? Бірігуге мысал келтір.
Бірігуді Эйлер-Венн диаграммасы арқылы кескінде.
Бірігудің қандай қасиеттерін білесің?

ІІ.14. Жиындардың айырымы. Толықтауыш жиын
Оқушыларға 5-3=2 болатындығын түсіндіру үшін мынадай тәсіл қолданылады. Мысалы, оқушыларға 5 дөңгелекше алу ұсынылады. Олар санау арқылы дөңгелекшелердің шынында да бесеу екендігіне кез жеткізеді. Осыдан кейін 3 деңгелекшені алып тастап, қалған доңгелекшелерді санап, нешеу қалғанын біледі. Сонда 2 дөңгелекше қалды. Ендеше 5-3=2.
Бүл тәсілдің мәні неде? а элементі бар қандай да бір жиынның b элементі бар белігін алып тастадық. Сонда берілген жиынның а-b бөлігі қалды.
Анықтама: А жәие В жиындарының айырымы деп А жиынына тиісті, бірақ В жиынына тиісті емес элементтерден тұратын жиынды айтамыз. Мұндағы ВсА.
Жиындардың айырымын былай белгілейді: А\В, \ -айырым белгісі. А және В жиындарының айырымын Эйлер-Венн диаграммасы арқылы кескіндесек, онда А жиынына тиісті, бірақ В жиынына тиісті емес бөлік -штрихталған бөлік болады.

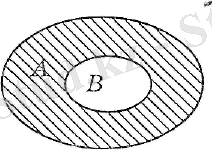
Ескерту: Тең жиындардың айырымы бос жиынға тең.
Мысал: А={а,b,с,d), В={с,b,d,а} А=В екені көрініп тұр. А және В жиындарының айырымын табамыз: А\В=Ø өйткені, А жиынына тиісті, бірақ В жиынына тиісті емес элементтер жоқ.
Жиындардың айырымын кейбір жағдайда толықтауыш жиын деп те атайды және оны былай белгілейді: ВА, оқылуы. В жиынының А жиынына дейінгі толықтаушы.
Мысал:А={1,2,3,4,5,6},В={1,3,5}.А\В ={2,4,6}немесе ВА={2,4,6}.
Егер жиын элементтерін атап жазып көрсету арқылы бергенде жиындардың айырымы қалай табылатындығын білеміз. Егер жиын, оның элементтерінің сипаттамалық қасиеті арқылы берілсе, онда А\В жиынының сипаттамалық қасиеті хEuroАжәне хEuroВ түрінде болады.
Мысалы А - жұп сандар жиыны, ал В - 4-ке бөлінетін сандар жиыны болсын. А\В жиынына 20 және 26 сандарының тиісті емес екендігін анықтайық. 4-ке бөлінетін сандардың барлығы жұп сандар болғандықтан ВсА.
Егер А жиынынан 4-ке бәлінетін барлық сандарды алып тастасақ, онда 4-ке бөлінбейтін жұп сандар қалады. Яғни А\В - жиыны 4-ке бөлінбейтін жұп сандар. Бұл жиынның элементтерінің сипаттамалық қасиеті -жұп сан болуы және 4-ке бөлінбейтіндігі.
20 саны жұп сан және 4-ке бөлінетін болғандықтан, 20EuroА\В екендігін байқау қиын емес, ал 26 саны жұп сан, бірақ 4-ке бөлінбейтін болғандықтан 26EuroА\В болады.
Енді А - жұп сандар жиыны, В-4-ке бөлінетін сан-дар жиыны, ал С - 6-ға бөлінетін сандар жиыны болған жағдайда А\В∩С жиыны қандай сандардан тұратынды-ғын анықтайық.
А\В∩С жазуында жақшалар жоқ. Ендеше, қайсы амал бүрын орындалады? деген заңды сұрақ туады. Мұндай жағдайда қиылысу амалы айырым амалына қарағанда күгптірек деп есептеледі. Сондықтан А\В∩С жазуында қиылысу амалын бұрын орындаймыз. В және С жиындарының қиылысуында 4-ке де, 6-ға да бөлінетін жұп сандар болады (бір мезгілде). Егер А жиынынан В және С жиындарының қиылысуын алып тастасақ, онда А жиынында 4-ке де, 6-ға да бір мезгілде бөлінбейтін жұп сандар қалады. Мұны Эйлер дөңгелектерінің көмегімен былай көрсетуге болады:

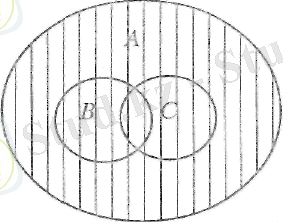
Сонда А\В∩С жиыны штрихталған бөлік болып есептеле-ді. Бұл жиынға В∩С жиыны кірмейтіндігі диаграммадаи көрініп тұр.
Тексеру сұрақтары:
А және В жиындарының айырымы деп нені айтамыз?
Жиындардың айырымын басқаша қалай атайды?
Жиындардың айырымын Эйлер-Венн диаграммасы арқылы қалай керсетуге болады?
ВА жазуы қалай оқылады?
Тең жиындардың айырымына мысал келтір.

17. 15. Жиындардың декарттық көбейтіндісі
Бастауыш сыныптарда оқушыларға мынадай тапсырма беріледі: 1,2 және 3 цифрларын пайдаланып барлық мүмкін болатын екі таңбалы сандарды жаз.
Сонда: 11 12 13
21 22 23
31 32 33
Бұл жазудағы әрбір сан екі цифрдан құралған және олардың орналасуында белгілі рет, тәртіп сақта.лған. Мысалы, 1 және 2 цифрларынан әр тұрлі екі сан алынған. Олар: 12 және 21.
Жиын элементтерінің орналасу тәртібі маңызды болатын жағдайды математикада әлементтердің реттелген жиынтығы деп айтады. Жоғарыда берілген тапсырмада біз іс жүзінде реттелген пар ұғымымен кездесіп тұрмыз. Пар -- қос, жұп, екеу деген мағына береді.
А және В элементтерінен құрылған (жасалғаң) реттелген парды (а,b) деп белгілеу келісілген. Мұндағы, а- 1-ші координата немесе 1-ші компонент, ал b - 2-ші координата немесе 2-ші компонент деп аталады.
(а,b ) және (с, d) парлары а=с және b=d, болған жағдайда ғана тең болады. Реттелген пардың компоненттері өзаратеңболуы дамүмкін, яғниа a=b. Мысалы, 11, 22,33 сандарын мынадай реттелген парлар тұрінде қарастыруға болады: (1, 1), (2, 2), (3, 3).
Жоғарыда қарастырылған тапсырмада біз іс жүзінде {1, 2, 3} элементтерінен тұратын жиынға амал қолдану арқылы реттелген парларды құрдық. Сондай-ақ әр түрлі екі жиын элементтерінен де реттелген парлар құруға болады. Мысал: А={1, 2, 3} және В={5, 6} жиындары берілсін. Осы жиын элементтерінен 1-ші компоненті А жиынынан, ал 2-ші компоненті В жиынынан алынған мүмкін болатын барлық парларды жазайық. Сонда: {(1, 5), (1, 6), (2, 5), (2, 6), (3, 5), (3, 6)} реттелген парлар тұріндегі жаңа жиын алдық. Бұл жаңа жиынды А және В жиындарының декарттық көбейтіндісі деп атайды.
Анықтама: А лсәне В жиындарының декарттық көбейтіндісі деп, бірінші компоненті А жиынынаы, ал екінші компоненті В жиынынан алынған реттелген парларды айтады.
Жиындардың декарттық көбейтіндісін былай белгілейді:

Жиындардың декарттың көбейтіндісі орын ауыстырымдылық және терімділік заңдарына бағынбайды. Яғни, АхВ =ВхА және Ах(ВхС) = (АхВ)хС.
Жиындардың декарттық көбейтіндісі үшін бірігу амалына байланысты үлестірімділік заңы орындалады: (АUВ)хС = (АхС) U (ВхС).
Жиындардың декарттық көбейтіндісін кейбір жағдайда тік бұрышты таблица түрінде жазған ыңғайлы: мысалы, А={1, 2, 3}, В={5, 6} жиындарының декарттық көбейтіндісін мынадай түрде беруге болады:
АВ
5
6
1
(1,5)
(1,6)
2
(2,5)
(2,6)
3
(3,5)
(3,6)

Математикада тек реттелген нарлар ғана емес, сондай-ақ үш, төрт және одан да көп элементтерден құралған жиынтықтар да қарастырылады. Осындай реттелген жиынтыңтарды кортеждер деп атайды.
Кортежге енетін элементтердің санын кортеждің ұзындығы деп атайды. Мысалы, (1, 5, 6) - кортежінің ұзындығы 3-ке тең, өйткені ол үш элементтен тұрады, ал (7, 8, 9, 4, 3) - кортежінің ұзындығы 5-ке тең, өйткені ол 5 элементтен тұрады.
Кортеж ұғымын пайдаланып, n жиынның декарттың көбейтіндісін анықтауға болады.
Анықтама: Ах,А2,...,Ап жиындарының декарттық көбейтіндісі деп бірініпі компоненті Ах жиынынан, екінші компоненті А2 жиынынан алынған ұзындығы n -ге тең кортежді айтады.
n жиынның декарттың кебейтіндісін былай белгілейді: Аг х А2 х ... х Ап. Мысал: А,={2,3} , А2={3,4,5} , А3={7,8} жиындарының декарттың көбейтіндісін табайық:
АгхА2хА3 = {(2,3,7), (2,3,8), (2,4,7), (2,4,8), (2,5,7), (2,5,8), (3,3,7), (3,3,8), (3,4,7), (3,4,8), (3,5,7), (3,5,8)}.
Бұл үш жиынның декарттың көбейтіндісінде ұзындығы 3-ке тең кортеждер алдық.
Тексеру сұрақтары:
1. Реттелген пар ұғымын қалай түсінесің? Оны жалпы түрде қалай белгілейді?
(а,b ) жазуындағы а мен b-ның атаулары Қандай?
Жиындардың декарттың көбейтіндісін аныҚта. Мысал келтір.
4. Жиындардың декарттың көбейтіндісін басқаша қалай жазуға болады?
Кортеж ұғымын қалай түсінесің?
Кортеждің ұзындығы дегеніміз не?
п - жиынының декарттық кебейтіндісі қалай анықталады?

17. 16. Жиындарды өзара қиылыспайтын ішкі жиындарға бөліктеу ұғымы
Жиын ұғымы және оларға қолданылатын амалдар бізге классификациялау (топтастыру) жөніндегі түсінігімізді нақтылай түсуге мүмкіндік береді.
Классификация - бұл кластар ішіндегі объектілердің ұқсастығы және олардың басқа кластар объектілерінен айырмашылығы (ерекшелігі) негізінде объектілерді кластарға бөлу амалы.
Классификацияның мақсаты - біздің білімдерімізді жүйелеу болып табылады.
Классификация ұғымы ғылымының барлық дерлік саласында қолданылады. Мысалы, зоологияда жануар-ларды классификациялау, биологияда өсімдіктерді классификациялау жүргізіледі.
Классификация ұғымы математикада өте кеңінен қолданылады. Мысалы, натурал сандарды жұп сандар және тақ сандар, т.б.; бұрыштарды сүйір, доғал, тікбұрыш, т.б. деп бөлуге болады. Жалпы, дұрыс орындалған классификация қандай шарттарды қанағаттандыруы тиіс?
Кез келген классификация қандай да бір объектілер жиынын ішкі жиындарға бөліктеумен (бөлумен) байла-нысты. Егер берілген жиынның әрбір элементі бір, тек қана бір ішкі жиынға ғана тиісті болса, ал бөлініп алын-ған ішкі жиындардың бірігуі берілген жиынмен дәлме-дәл келген жағдайда берілген жиыы өзара қиылыспайтын ішкі жиындарға немесе кластарға бөлінді деп ай-туға болады. Сонымен, қандай да бір х жиынын өзара қиылыспайтын хг х2, хг,...,хп ішкі жиындарға бөліктеу ғ.елесі шарттарды қанағаттандыруы тиіс.
Ішкі жиындардың бірде біреуі бос болмауы тиіс.
хх, х2, х3,...,х ішкі жиындары езара қиылыспауы керек. Басқаша айтқаяда, ішкі жиындардың қиылы-суы бос жиынға тең болуы керек.
хх, х2, х3,...,хп ішкі жиындарының бірігуі берілген х жиынымен дәлме-дәл келуі керек. Басқаша айтқан-да, ішкі жиындарды біріктіргенде, берілген х жиыны шығуы тиіс.
Егер аталған шарттардың ең болмағанда біреуі орындалмаса, онда классификация дұрыс орындалма-ған деп есептеледі.
X - үшбұрыштар жиынын сүйір бұрышты, тікбұрыш-ты және доғал бұрышты деп үш класқа бәлуге болады. Расында да, бәлініп алынған ішкі жиындар өзара қиылыспайды. Сүйір бұрышты үшбұрыштардың арасында тікбұрышты және доғал бұрышты үшбұрыштар, тікбұрышты үшбұрыштардың арасында сүйір бұрышты және доғал бұрышты үшбұрыштар, т.с.с. жоқ және оларды біріктірсек, қайтадан X - үшбұрыштар жиынының өзі қайтадан шығады.
Дегенмен, берілген жиынның кез келген ішкі жиындар жүйесі, сол жиынды ішкі жиындарға бөлуді көрсете алмайды. Мысалы, егер X - үшбұрыштар жиынының тең бүйірлі және тең қабырғалы үшбұрыштар деген ішкі жиындарын бөліп алсақ, онда X жиынын ішкі жиындарға (кластарға) бөлдік деп айта алмаймыз, өйткені бұл ішкі жиындар өзара қиылысады.

Сонымен классификация жиынның ішкі жиынын бөліп алумен байланысты екен. Біраң ішкі жиындарды бөліп алу үшін, оның элементтерінің сипаттамалық қасиетін көрсету жеткілікті. Мысал ретінде N натурал сандар жиынын қарастырайық. Оның әлементтері әр түрлі қасиеттерге ие бола алады. Атап айтсақ, натурал сандардың ішінде жұп сандар, тақ сандар, 3-ке бөлінетін, 5-ке бөлінетін, т.б. сандар бар. Айталық, бізге 3-ке бөлінгіштік қасиеті бар сандар керек болсын. Сонда басқа натурал сандар туралы олар 3-ке бөлінбейді деп айтуға болады, яғни бізде натурал сандар-дың тағы бір ішкі жиыны пайда болды. Бөлініп алынған ішкі жиындар өзара қиылыспайды, ал олардың бірігуі N натурал сандар жиынымен дәлме-дәл келеді.

Сонымен, натурал сандар жиынының бір қасиетін көрсету бұл жиынды екі ішкі жиынға: 3-ке бөлінетін сандар жиыны (мысалы, 3,6,9,12, т.б.) және 3-ке бөлінбейтін натурал сандар жиынына бөлді.
Егер жиын элементтерінің екі қасиетін көрсетсе, яғни жиынның екі ішкі жиынын бөліп алу керек болса, онда кластарға бөлу қандай түрде болады?
Натурал сандар жиынының екі қасиетін көрсетейік: 1) З-ке бөлінгіштік жөне 5-ке бөлінгіштік. Аталған қасиеттердің көмегімен натурал сандар жиынының екі ішкі жиынын бөліп алуға болады: А- 3-ке бөлінетін сандар жиыны, В - 5-ке бөлінетін сандар жиыны. Бұл жиындар өзара қиылысады, бірақ олардың бірде-біреуі екіншісінің ішкі жиыны бола алмайды.

Суреттен N натурал сандар жиыны өзара қиылысытын 4 бөлікке бөлінетінін көреміз. Олар рим цифрлар мен нөмірленген. Әр бөлік N натурал сандар жиынының ішкі жиынын кәрсетеді. Енді әрбір ішкі жиында қандай сандар болатындығын анықтайық. 1-ішкі жиын -3-ке және 5-ке бәлінетін сандардан; 2-ішкі жиын - 3-ке бөлінетін және 5-ке бөлінбейтін сандардан; 3-ішкі жиын - 5-ке бөлінетін және 3-ке бөлінбейтін сандардан; 4-ішкі жиын - 3-ке бөлінбейтін және 5-ке де бөлінбейтін сандардан құралған. Бұл төрт ішкі жиынның бірігуі N натурал сандар жиынын береді.
Сонымен, натурал сандар жиынының екі қасиетін көрсету, бұл жиынды 4 класқа бөлінуге әкелді. Олар:
3-ке және 5-ке бөлінетін сандар;
3-ке бөлінетін және 5-ке бөлінбейтін сандар;
5-ке бөлінетін және 3-ке бөлінбейтін сандар;
3-ке және 5-ке бөлінбейтік сандар.
Жиын элементтерінің екі қасиетін көрсету жиынды міндетті түрде 4 класқа бөлуге әкеледі деген теріс ұғым қалыптаспауы тиіс. Бұл әрқашан бола бермейді. Мысалы, үшбұрыштар жиыны тікбұрышты болу және доғал бұрышты болу деген екі қасиеті бойынша үш класқа бөлінеді. Олар:
Тік бұрышты үшбұрыштар жиыны;
Доғал бұрышты үшбұрыштар жиыны;
Тік бұрышты да, доғал бұрышты да болмайтын үшбұрыштар жиыны.
Бұл белінуді диаграмма арқылы былай көрсетуге болады.

Тексеру сұрақтары:
1) Классификация сөзінің мағынасын қалай түсінесің?
Жиындарды өзара қиылыспайтын ішкі жиындарға бөліктеу қандай шарттарды қанағаттандыруы тиіс?
N - натурал сандар жиынын қандай қасиеттері бойынша ішкі жиындарға бөліктеуге болады?
4) Топ студенттерінің жиынын қандай белгілері (қасиеттері) бойынша өзара қиылыспайтын ішкі жиындарға бөліктеуге болады?

П. 17. Жиындардың декарттың көбейтіндісін координаттың жазықтықта кескіндеу
Жиын элементтерінің саны шектеулі болған жағдайда олардың декарттық көбейтінділерін табу қиын емес. Егер жиын элементтерінің саны шектеусіз болған жағдайда декарттық көбейтіндіні қалай табуға болады?
Мысалы, 3-тен және 5-тен артық натурал сандар жиындарының декарттық көбейтіндісін қалай көрсетуге болады. Бұл жағдайда Эйлер дөңгелектері де көмектесе алмайды.
Математикада бұл жағдайдан щығудың жолы табылған. Қандай да екі сан жиындарының декарттың көбейтіндісін координаттық жазықтықта кескіндеп көрсетуге болады екен. Бұл қандай түрде болады? Бұл сұраққа жауап беру үшін, алдымен координаттық түзу және координаттық жазықтық ұғымдарын есімізге түсірейік.
Координаттык тузу деп - берілген санақ басы, ұзындық бірлігі және оң бағыты бар түзуді айтамыз.
Координаттық түзуде нүктенің координаты қалай анықталады?

I түзуінің бойынан О нүктесімен дәлме-дәл келмейтін (беттеспейтін) М нүктесін алып, оған х санын сәйкестендірейік. Сонда:
х санының модулі О нүктесінен М нүктесіне дейінгі қашықтыққа тең.
Егер М нүктесі О нүктесінің оң жаң бөлігінде орналасса, х - оң сан, ал О нүктесінің сол жағында жатса, онда х - теріс сан.
Сонымен, анықталған х саны М нүктесінің координаты деп аталады және былай жазылады: М (х). Мысалы суретте

М нүктесінің координаты 4, ал К нүктесінің координаты (-2)-ге тең. Оны былай жазамыз. М (4); К (-2). Егер М нүктесі О нүктесімен беттесетін болса, онда оның координаты 0-ге тең деп есептеледі және былай жазылады: М (0).
Сонымен, координаттың түзудің енгізілуіне байланысты түзудің нүктелері мен нақты сандарының арасындағы байланыс тағайындалады:
Координаттық түзудің кез келген М нүктесіне бір ғана х нақты саны - осы нүктенің координаты сәйкес келеді, немесе керсінше: әрбір нақты саны координаты бар бір ғана М нүктесіне сәйкес келеді.
Өзара перпендикуляр орыаласқан, бір нүктеде қиылысатын және ОЕ1 = ОЕ2 болатын ұзындық бірліктері бар Ох және Оу екі координаттық түзу алайық. Ох және Оу түзулері тік бұрышты координаттар жүйесінің осьтері деп
аталады.
Ох -- абсцисса осі, ал Оу - ордината осі. Түзулердің қиылысу нүктесі О - координата басы деп аталады.
0 нүктесіне байланысты Ох осі екі жарты жазықтыққа бөлінеді. Абсцисса осінде О нүктесінің оң жағында оң мәндер, ал сол жағында теріс мәндер орналасады. О нүктесіне байланысты Оу осі де екі жарты жазықтыққа бөлінеді. О нүктесінің жоғарғы жағында оң мәндер, ал төменгі жағында теріс мәндер орналасады.
Координаттық жазықтықта нүктенің координатасы қалай анықталады?
Координаттың жазықтықта қандай да бір М нүктесін алайық. М нүктесінің орны екі санмен анықталады. Олар: абсцисса және ордината. М нүктесінің
абсциссасы Ох осінің бойында, ал ординатасы Оу осінің бойында орналасқан.
Егер х саны М нүктесінің абсциссасы, ал у саны оның ординатасы болса, онда М нүктесінің х және у коорди-натасы бар деп атайды және былай жазады: М (х; у).
Сонымен, тік бұрышты координаттар жүйесінде жазықтықтың әрбір нүктесіне бір ғана нақты сандар пары сәйкес келеді немесе керсінше, әрбір (х; у) парына жазықтықтың бір ғана М нүктесі сәйкес келеді.
Тік бұрышты координаттар жүйесін математикаға алғаш енгізген француз ғалымы Рене Декарт (1596-1650 жж.) болған. Осы кісінің құрметіне тік бұрышты координаттық жазықтықты декарттың координаттық жазықтық деп те атайды.
Координаттық жазықтықтағы нүктенің координатасы декарттық кебейтіндінің парларына ұқсас екендігін байқадық. Ендеше, жиындардың декарттың көбейтіндісін координаттық жазықтықта бейнелеп көрсетуге болады екен.
Жиындардың декарттық көбейтіндісін координаттың жазықтықта кескіндеу мысалдарын қарастырайық.
1-мысал. А={1, 2, 3}, В ={3, 5} болсын. Мұнда жиын элементтерінің саны шектеулі. Сондықтан олардың декарттың көбейтінділерін жазып көрсетуге болады:
АхВ ={(1,3), (1,5), (2,3), (2,5), (3,3), (3,5)}.
Координаттық жазықтық алып, Ох осінің бойында А жиынының элементтерін Оу осінің бойында В жиынының әлементтерін белгілейміз. АхВ декартт ың көбейтінділердің парларын координаттық жазықтыққа саламыз. Сонда алты нүктеден тұратын фигура А және В жиындарының декарттық көбейтіндісінің көрнекті түрде бейнеленуі болады.
2-мысал. А ={1, 2, 3}, В = [3; 5]. Вүл жағдайда декарттық көбейтіндінің барлық парларын жазып шығу мүмкін емес, өйткені В жиынының әлементтерінің саны шексіз. Бірақ бұл декарттық көбейтіндінің жасалу про-цесін көрсетуге болады.
Ол үшін әрбір пардың бірінші компоненті не 1, не 2, не 3 сандары болады, ал екінші компонент [3; 5] аралығынан алынған нақты сан. Бірінші компоненті 3-пен 5-тің ара-сындағы сандар болатын барлық парлар, РМ кесіндісінің нүктелерімен бейнеленеді, ал бірінші компоненті 2 саны, екінші компоненті [3; 5] аралығындағы сандар болатын барлық парлар КL кесіндісінің нүктелерімен, ал бірінші компоненті 3 саны, ал екінші компоненті [3; 5] аралығындағы сандар болатын барлық парлар QS кесіндісінің нүктелерімен бейнеленеді. Сонымен 2-мысалдағы А және В жиындарының декарттық көбейтіндісін координаттың жазықтықта РМ, КL, QS кесінділері түрінде бейнеленеді.

3-мысал. А = [1, 3], В = [3, 5]. Мұнда А жиынының да В жиынының да элементтерінің саны шектеусіз. Сондықтан декарттың көбейтіндінің 1-ші компоненті [1,3] кесіндісінің шеткі нүктелері ғана емес, осы аралықтағы барлық сандар болады. Сондықтан, АхВ декарттық көбейтіндісі КLМР шаршысымен бейнеленеді. ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.