Қайтымды және қайтымсыз процестер

Пән: Физика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 17 бет
Таңдаулыға:

Қайтымды және қайтымсыз процестер.

Тұйық процестер (цикл)

Егер термодинамиканың бірінші бастамасы энергияның бір түрден екінші түрге өзгергенінде байқалатын сандық қатынастарды көрсетср, екінші бастамасы осы энергияның өзгерістері қандай жағдайларда жүзеге асатынын анықтайды, яғни процестердің қандай бағытта өтуі мүмкін екенін көрсетеді. Сонымен қатар термодинамикада тепе - тең күй ұғымы сияқты, қайтымды процестер ұғымының да ролі зор.

Қайтымды процесс деп кері бағытта өткізуге болатын процесті тура бағытта өткізгенде және қандай күйлерден өтсе, кері бағытта сондай күйлер тізбегінен өтетін процесті айтады. Сөйтіп қайтымды процеске тек тепе-тең процестер жатады. Сонда қайтымды процесс әуелі бір бағытта, содан соң кері бағытта бірінен соң бірі болып отыратын тепе-тең күйлердің үздіксіз тізбегінен құрылуы, сөйтіп жүйені қоршаған денелерде ешқандай өзгеріс болмауы тиіс.

Тепе-тең емес процестер әрқашанда қайтымсыз процесс, дәл-деп айтқанда нақты процестер қайтымсыз процестер болады. Олар мейлінше баяу өте отырып, қайтымды процестерге тек жуықтай.

Қайтымды және қайтымсыз процестер. Қайтымды процесс деп екі бағытта да өте алатын процесті атағанбыз, бірақ процесс әуелі бір бағытта өтіп, сонан кейін кері бағытта өткен болса, онда система, айналадағы денелерде қандай да бір өзгерістер болмастан, бастапқы күйіне оралуға тиіс.

Қайтымды процеске мысал келтірейік. Абсолют серпімді ауыр шар көлбеу жазықтыққа А нүктесінде бекітулі тұрған болсын (184-сурет) . Көлбеу жазықтық жиегіне қозғалмастай оған нормаль етіліп абсолют серпімді қабырға (қалқан) орнатылған делік. Егер шарды босатып жіберсек, ол көлбеу жазықтықтың бетімен домалап барып В қабырғасына соғылады да, ол қабырғадан серпіліп, қайтадан көлбеу жазықтықпеп домалап, А нүктесіне келеді. Бұл жерде процесс бүтіндей қайталап отыр: айналадағы денелерде қандай да бір өзгерістер болмастан, шар қайтадан А нүктесіне

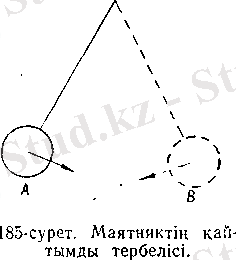
оралды. Үйкеліссіз тербеліп тұрған маят- никтің қозғалысын да осындай қайтымды процестің мысалы деп қарастыруға болады: маятник (185-сурет) өзінің жарты период ішінде А нүктесінен В нүктесіне

дейін жүрген жолын екінші жарты, период ішінде кері бағытпен қайта жүріп өтеді және А нүктесіне айналадағы денелерде қандай да бір өзгерістер болмастан оралады. Жалпы алғанда, үйкеліссіз өтетін және серпімсіз соқтығулар қатыспайтын нағыз (таза) механикалық процестердің барлығын да қайтымды процесс деп айтуымызға болады.

Карноның идеал циклын қарастырғанда, қандай да бір Q ₁ - Q ₂ жылу мөлшерін А жұмысқа қайтымды түрде айналдыруға болатындығын байқадық, бірақ бұл айналдыру анағұрлым күрделі

бір процестің жеке ғана буыны (кезеңі)

болып табылады: ол айиалу кезінде қыздырғыш -

тан суытқышқа Q ₂ жылу мөлшері ауысады.

Суытқыш машипапы жасау үшін Карноның

сол қайтымды циклын пайдаланып, біз А

жұмысы есебінен Q ₁ - Q ₂ жылу мөлшерін қайта шығарып алуымызға және суытқыштан қыздырғышқа Q ₂ жылу мөлшерін кері кешіруімізге болады. Алайда мұны Карно циклы тепе-тең, яғни шексіз баяу өткенде ғана жүзеге асыруға болатындығын атап көрсетеміз, ал Карно циклын практикада ондай түрде жүзеге асыруға болмайды. Жұмыс жылуға айналатын нақты жағдайлардың қай-қайсысында болса да бұл құбылыс қайтарымсыз түрде өтеді, өйткені жұмысты өздігінен, басқа бір бөгде процестердің өтуімен байланыстырмай-ақ жылуға айналдыруға болғанмен, жылуды жұмысқа айналдыру үшін қандай да бір басқа процестердің өтуі қажет.

Қайтимсыз процесс деп оған кері процесс анағұрлым күрделі процестің кезеңдерінің (буындарының) бірі ретінде ғана өте алатын процесті айтады.

Сөйтіп, қайтымсыз процестер үшін олардың қай бағытта өтетіндігінің үлкен мәні бар. Бір бағытта, оны біз «оң» бағыт деп атайтын боламыз, бұл процестер «өздігінен» өтсді, яғни тұйықталған системада өтіп отырған бірден-бір ғана процесс бола алады. Екінші, қарама-қарсы бағытта, оны біз «теріс» бағыт деп атайтып боламыз, ол процестер басқа бір «оң» процеспен селбесіп қана өте алады. Мысалы, жұмыс қандай жағдайда болса да әрдайым «өздігінсн» жылуға айаалады. Үйкеліс күштері қатысатын немесе денелер бір-біріне серпімсіз әсер ететіп жағдайлар кездесетін процестердің барлығыпда да істелген жұмыстың есебінен жылу пайда болады. Ал жылудың жұмысқа айналуын тек анағұрлым күрделі процостің бөлігі (кезеңі) ретінде ғана байқауға болады. Карно циклы немесе оған ұқсас басқа бір процесс орындалғанда, жылудың жұмысқа айналуымен қабат жылу ыстық денеден (қыздырғыштан) суығырақ денеге (суытқыщқа) ауысып, «оң» процесс те селбесе өтеді.

Жылудың ыстық денеден суық денеге көшуі де (жылу өткізгіштік құбылысы да) қайтымсыз процесс болып табылады. Денелердің температураларының теңделуіне келіп тірелетіп бұл процесс те «өздігінен» өтеді, яғни тұйықталған системада өтетін бірден-бір процесс бола алады. Ал бұған кері «теріс» процесс - суық денеден жылудың ыстық денеге көшуі - «өздігінен» болмайды. Суытқыш машинаны пайдаланғанда жылу суығырақ денеден ыстығырақ денеге көшу үшін мұнымен қатар «оң» процестің өтуі қажет, бұл процесте А жұмыс істелініп, ол жұмыс қыздырғышқа берілетін

\[{\mathcal{I}}{\mathcal{I}}\]

Q ₁ жылу мөлшеріне айналады.

Қайтымсыз түрде өтетін процестің тағы да бір мысалы ретінде газдың бостықта ұлғаю құбылысын келтіруге болады. Бір ыдыс (186-сурет) аралық (С) қабырғамен тец екі бөлікке (А мен В бөліктеріне) бөлінген делік. А бөлігінде газ, В бөлігі бос болсын. Егер аралықты алып қойсақ, газ лезде «өздігінен» ұлғаяды да, В бөлігіне өтіп, бүкіл ыдыстың ішіне бір қалыпты тарайды. Ал осы газды қайтадан сығып А бөлігіне қамау үшін, сыртқы күштердің жәрдемімен қандай да бір жұмыс істеу қажет. Бұл жұмыстың нәтижесінде газ қызады, яғни газды сыққандағы «теріс» процесс жылудың жұмысқа айналуындағы «оң» процеспен селбесе өтетін болады.

Газ ұлғайғандағы «оң» процесс жылу жұмысқа айналғандағы селбесе өтіп отыратын процесс болып табылуы мүмкін. Мысалы, газ изотермиялық түрде ұлғайғанда оған сырттан берілетін жылудың барлық Q мөлшері А жұмысқа айналады; бұл құбылыста жылудың ыстық денеден суығырақ денеге көшуі деген атымен жоқ, бірақ оның есесіне газдың қайтарымсыз («оң») ұлғаю құбылысы байқалып отыр. Сөйтіп, «теріс» процестің қай-қайсысы болса да бір «оң» процеспен өтеліп (компенсациланып) отыруы шарт.

Термодинамиканың бірінші бастамасы.

Берілген жылу мөлшері мен жұмыстың арасындағы эквиваленттік механикалық энергияның сақталу заңын жалпылап топшылауға мүмкіндік береді. 28-параграфта айтқанымыздай, системаның механикалық энергиясының өзгеруі ол системаға сырттан түсірілген күштер мен ішкі үйкеліс күштері өндірген жұмысқа пропорционал болады. Сонда біз жылу әсерлерін қарастырмаған едік. Жалпы жағдайды алғанда системаның знергиясы жұмыс өндіру нәтижесінде ғана өзгермей, жылу берілу есебінен де, басқа да әсерлердің (мысалы, жарықты сіңіру) есебінен де өзгеруі мүмкін.

Қандай да бір системаны қарастырайық және оны бір күйден екінші күйге түсіретін болайық. Мысалы, газдың белгілі бір мөлшері сыртқы күштердің әсерімен сығылуы мүмкін және сонымен қатар ол газға қандай да бір мөлшерде жылу берілу нәтижесінде оның қызуы да мүмкін. Системаның әрбір күйін сипаттайтын белгілі бір шамаларды тағайындап алу арқылы ол күйді макроскопиялық тұрғыдан анықтауға болады. Мұндай шамалар параметрлер деп аталады. Идеал газ үшін оның күйін анықтайтын мұндай параметрлер V көлем, р қысым және Т температура үшеуінің кез келген екеуі болады, өйткені идеал газдың берілген мөлшерінің күйін бұл үш шаманың кез келген екеуі (мысалы, р қысым мен Т температура) анықтайды.

Система бір күйінен екінші күйіне сыртқы әсерлердің ықпалымен көшеді, мұндай әсерлер болып табылатындар тек сыртқы күштердің жұмысы

\[\Delta A\]

ғана болып қоймай, жылудың қандай да бір мөлшері

\[\Lambda_{\bf d}\]

Q берілуі де, басқа да әсерлер болады. Жылу берілісі мен жұмыс, жоғарыда байқағанымыздай, әрқашан да бір-біріне эквивалентті болады. Тәжірибелерге қарағанда, басқа әсерлердің барлығы үшін де тиісті механикалық эквиваленттер тағайындауға болады. Ол - ол ма, тәжірибелерге қарағанда, сыртқы әсерлердің ықпалымен система белгілі бір күйінен (I) басқа белгілі бір күйіне (II) көшетін болса, онда мұндай көшулердің мүмкін тәсілдерінің барлығында да сыртқы әсерлердің механикалық эквиваленттерінің қосындысы өзгермей тұрақты болып қала береді.

Энергияның өзгерісін анықтайтын осы қосынды, яғни сыртқы әсерлердің механикалық эквиваленттерінің қосындысы

\[\textstyle{\sum}\Delta A\]

мен энергияның өзгерісі U _н - U ₁ арасында мынадай қатыс болады:

\[U_{t}\,\cdot\,U_{1}=r{\textstyle\sum}A A_{i}.\]

мұндағы U ₁ мен і U ₂ - системаның І және ІІ күйіндегі энергиялары, ал r - пропорционалдық коэффициент.

Бұл айтылғанға қарағанда, физикалық мағынасы бар шама системаның екі күйі энергияларының айырмасы болып табылады, ал энергияның өзін системаның қандай да бір күйінің энергиясын шартты түрде ноль деп (немесе белгілі бір мәні бар деп) алғанда ғана анықтауға болады. Ал егер системаның қандай да бір күйінде оның энергиясының белгілі бір мәні бар деп алсақ, мысалы, І күйінде энергия мәні U ₁ болса, онда ІІ күйінде системаның энергиясы Uн (1) формула бойынша мынаған тең болады:

\[U_{t}\,\cdot\,U_{1}=r{\textstyle\sum}A A_{i}.\]

Жоғарыда айтқанымыздай,

\[\textstyle\sum\!\Delta A_{1}\]

қосындысы системаның І күйінен ІІ күйіне қандай тәсілмен көшетіндігіне байланысты болмайды, сонымен системаиың // күйінде энергияның да дәл анықталған Uн мәні болады. Бұл - энергия күйдің бір мәнді функциясы болып табылады, яғни энергия да күйді анықтайтын параметрлермен анықталады деген сөз. Егер қандай да бір әсерлердің нәтижесінде система әуелі / күйінен // күйіне көшіп, сонан кейін қайтадан / күйіне түссе, онда системаның энергиясы бұрынғы мәніне ие болады. Демек, энергияның өзгеру және сақталу заңын ең жалпы түрде былайша тұжырымдап айтуға болады: система бір күйінен екінші күйіне көшкенде оның энергиясының өзгеруі сол көшуді туғызатын барлық сыртқы әсерлердің механикалық эквиваленттрінің қосындысына пропорционал болады. Дөңгелек процесте, яғни система өзінің бастапқы күйіне қайта оралатын процесте, барлық сыртқы әсерлердің механикалық эквиваленттерінің қосындысы нольге тең болады да, энергия тұрақты болып қала береді.

Осындай жалпы түрде айтылған энергияның сақталу заңы термодинамиканың бірінші бастдмасы деп аталады.

Нақтысында энергияның жылу өткізгіштік арқылы бсрілуінің маңызы көбірек болатындықтан, біз жылудың

\[\Lambda_{\bf d}\]

Q мөлшерінің берілуіне әкеп соғатын әсерлерді өз алдына жеке қарастыратын боламыз, сонда термодинамиканың бірінші бастамасын мына түрде жазамыз:

\[\mathbb{D})U\;_{-}~~y\mathbb{D}\mathrm{d}+\,J^{*}{\phi}\mathrm{d}{\Omega}_{2}\]

мұндағы

\[\Lambda_{\bf d}\]

U - системаның шікі энергиясының өзгерісі,

\[\Lambda_{\bf d}\]

Q - системаға берілген жылу мөлшері, ал

\[\Lambda_{\bf d}\]

А - басқа барлық сыртқы әсерлердің механикалық эквиваленттерінің қосындысы. Егер басқа сыртқы әсерлердің өзі механикалық әсер болса, онда

\[\Lambda_{\bf d}\]

А системаға түсірілген сыртқы күштердін жұмысы болып табылады.

Берілген жылу мөлшері мен жұмыс өз ара эквивалентті болатындықтан, жылудың берілген

\[\Lambda_{\bf d}\]

Q мөлшерін де жұмыс бірліктерімен (яғни эрг, джоуль, кГм т. с. ) өлшеуге болады, энергия да осы бірліктермен өлшенеді. Егер (2) формулаға кіретін шамалардың барлығын да бір ғана бірлікпен өлшейтін болсақ, онда k мен k' коэффициенттердің екеуі де бірге тең болады да, (2) формула мынадай түрде жазылады:

\[\textstyle\int\!\!\!\!\!\sqcup U\,-\,\textstyle\ D\!A+\Delta\!\!\!/\partial.\]

\[d U\,-\,d A+\Delta Q.\]

Системаның ішкі энергиясының өзгерісін шектеусіз аз деп санап, (2а) қатысты мынадай түрде жазамыз:

Система энергиясы U оның күйінің функциясы болып табылатындықтан және дөңгелек процесте энергияның өзгерісі нольге тең болатындықтан, dU толық дифференциал болып табылады. Жылыну құбылысы болатын барлық жағдайда да тұйық жолда өндірілетін жұмыс нольге тең болмайды. Бұдан ондай жағдайларда dU толық дифференциал болмайды деген қорытынды шығады. Олай болса, (26) қатыс бойынша екінші қорытынды жасауымызға болады: берілген жылудың dQ мөлшері де толық дифференциал болмайды.

Бұған жұмыс та, берілген жылудың мөлшері де энергияға барабар емес деген қорытынды шығады. Олардың қосындысы энергияның өзгерісін анықтайды, олардың мағынасы да осы болады.

Системаға түсірілген сыртқы күштер өндіретіп

\[\Lambda_{\bf d}\]

А жұмыспен қатар система тарапынап сыртқы денелерге түсетіп күштер өндіретін

\[\Lambda_{\bf d}\]

А' жұмысты да қарастыруға болады. Ньютонның үшінші заңы бойынша

\[\Lambda_{\bf d}\]

А'= -

\[\Lambda_{\bf d}\]

А. (2а) формулаға

\[\Lambda_{\bf d}\]

А' шамасын енгізіп, ол формуланы мынадай түрде жазайық:

AQ=
\[\Lambda_{\bf d}\]
U+
\[\Lambda_{\bf d}\]
A'. (3)

Осындай түрде жазылғанда термодинамиканың бірінші бастамасы мынадай пікірді білдіреді: систсмаға берілген жылу оның ішкі энергиясын арттыруға және система тарапынан сыртқы денелерге түсетін күштер өндіретін жұмысқа жұмсалады.

Термодинамиканың бірінші бастамасын жылу мен жұмыстың эквиваленттігін тағайындауға негіз болған тәжірибелер де, бұл заңнан шығатын көптеген қорытындылардың бақыланатын фактілермен дәл келетіндігі де растап сипаттайды.

Термодинамиканың бірінші бастамасы

Бір дененің толық энергиясынан толық механикалық энергиясын шығарып тастағанда қалатын энергия оның ішкі энергиясы деп аталады. Демек, дененің ішкі энергиясы дегеніміз молекулалардың бейберекет (хаосты) қозғалысының кинетикалық энергиясынан, молекулалардың өзара әсерлесуінің потенциалдық энергиясынан жане ішкі молекулалың энергиясынан тұрады. Денелер жүйесінің ішкі энергиясы әрбір жеке денелердің ішкі энергиялары мен демелер жанасатын жұқа қабаттағы молекулалардың арасындагы өзара әсерлесу энергиясы болып табылады.

Ішкі энергия - жүйе күйінің функциясы. Демек, жүйе бір күйден екінші күйге өткен кеаде оның ішкі энергиясыныи өзгерісі әрқашан да ауысу жолына тәуелсіз, яғни жүйенің бір күйінен екінші күйіне келтіретін процесіне немесе процестер жиынына тәуелсіз, тек осы күйлердегі ішкі энергияның мәндерінің айырмасына тең.

Ішкі энергия (U) негізінен екі түрлі процестің: дененің А жұмыс істеуі мен денеге берілген Q жылу мөлшерінің есебінен өзгереді. Жұмыс істеу жүйеге әсер етуші сыртқы денелердің орынауыстыруымен қоса жүреді.

Денеге жылу беру сыртқы денелердің орын ауыстыруына тәуелді емес. Ішкі энергияның бұл жағдайдағы өзгерісі жылы дененің жеке молекулаларының салқынырақ дененің молекулаларына қарсы істеген жұмысының әсерінен болады. Бір денеден екінші денеге энергияның берілуіне әкелетін микроскопиялық процестердің жиынтығы жылу берілуі деп аталады.

Сонымен, жылу берілісі мен жұмыс, әрқашан да бір-біріне эквивалентті болады. Мысалы, сыртқы әсерлердің ықпалымен жүйe бір күйден (I) екінші күйге (2) көшетін болса, онда мұндай көшулердің мүмкін тәсілдерінің барлығында да сыртқы әсерлердің механикалық эквиваленттері қосындысы өзгермей тұрақты болып қалады. Сонда жүйе бір күйден екінші күйге кешкенде ішкі энергияның өзгерісі

\[\Lambda_{\bf d}\]

V = U ₂ - U ₁ жүйенің алған жылу мөлшері Q мен сыртқы күштерге қарсы жасалатын жұмыстың (А) айырмасына тең:

\[\Lambda_{\bf d}\]

U = Q - A

немесе

Q =

\[\Lambda_{\bf d}\]

U + A (51)

Осы түрде жазылған өрнек термодинамиканың бірінші бастамасының математикалық теңдеуі болып табылады. Бұдан мынадай қорытынды шығады: жүйеге берілген жылу мөлшері жүйенің ішкі энергиясының өзгерісіне және жүйенің сыртқы денелерге қарсы істерін жұмысына жұмсалады. Жүйенің істеген жұмысын немесе алған жылуын есептеген кейде қарастырылып отырған процесті әдетте әрқайсысы жүйе параметрлерінің аз ғана өзгеруіне сәйкес келетін бірнеше жай процестерге бөлуге тура келеді, сонда (5І) теңдеу осындай процестер үшін мынадай түрде жазылады:

\[d Q=d U+\tilde{\partial}A\]

мұндағы

\[\bigotimes\]

Q - элементар жылу мөлшері,

\[\otimes\]

А - элементар жұмыс, dU жүйенің ішкі энергиясының өсімшесі .

Жүйе энергиясы U оның күйінің функциясы болып табылатындықтан, d U толық дифференциал болады, ал

\[\bigotimes\]

Q, және

\[\otimes\]

A толық дифференциал бола алмайды. Берілген жылу мөлшері мен жұмыс өзара эквивалеитті болатындықтан, жылу мөлшері де жұмыс бірліктерімен, яғни джоульмен (Дж) өлшенеді.

Жылу берілісте алмасқан энергия Q жылу мөлшері деп аталады. Егер дене жылу беріліс тәсілімен басқа денелерге Q жылу мөлшерін берсе, оның ішкі энергиясы азаяды. Ішкі энергияның өзгерісі дененің массасына және температура өзгерісіне пропорционал (32. 1) . Сондықтан берілген жылудың мөлшері Q дененің массасына және

\[\Lambda_{\bf d}\]

Т температурасының өзгерісіне пропорционал: Q = ст

\[\Lambda_{\bf d}\]

Т (32. 3) .

Термодинамиканың бірінші бастамасын

изопроцестерге қолдану

Газдың күйін сипаттайтын үш параметрдің (p, V, Т) процесс кезінде әйтеуір біреуі тұрақты болып отарса, онда мұндай процестерді изопроцестер деп атайды. Олай болса, термодинамиканың көптеген мысалдарында: жылу двигательдерінің жұмысын есептеуде, суыту машиналарының жұмысы кезінде, қысқасы газдардағы процестер туралы көбірек айтуға болады.

I. Изохоралық процесс деп берілген газдың көлемі (V = const) тұрақты болғанда жүретін процесті айтамыз. Сонда ешқандай көлем өзгерісі болмайды да (dV = 0) газ сыртқы күштерге қарсы жұмыс жасамайды:

\[d A=\mathbf{\Sigma}_{1}^{2}\mathbf{\hat{p}}d V=0\]

Осы (І) процестің диаграммасын былайша кескіндеуге болады (19-сурет) . Мұндағы 1-2 газдың изохоралық қыздыру процесін, ал 1-3 газдың изохоралық суыну процесін көрсетеді.

Әдетте изохоралық процесс көлемі өзгермейтін, қабырғалары калың ыдыстың ішінде газды суыту немесе қыздыру арқылы орындалады. Термодинамиканың бірінші бастамасы бойынша
\[d Q=d V+d A,d A=0\]
болғандықтан, газды қыздыруға

19-сурет.

немесе суытуға берілген барлық жылу мөлшері тек газдың ішкі энергиясын арттыру үшін ғана жұмсалады:

\[d G=d U\]

(72)

Ал тұрақты көлемдегі жылу сыйымдылық:

\[c_{\nu}={\frac{1}{m}}{\times}{\frac{d Q}{d T}}={\frac{1}{m}}={\frac{d U}{d T}}\]

(73)

яғни идеал газдың ішкі энергиясының өзгерісі оның абсолют температурасының өзгерісіне тура пропорционал болады.

2. Изобаралық процесс . Бұл процесс берілген газдың қысымы (р = const) тұрақты болғанда жүреді. Оның диаграммасын р - V координаттары арқылы кескіндеп көрсетуге болады.

(20-cypeт) . Сонда 1-2 кесіндісі газдың изобаралық ұлғаюан көрсетеді де, штрихталған аудан изобаралық жұмыстың шамасын анықтайды:

\[A=\bigcup_{V_{1}}{\mathsf{P}}d V=p(V_{2}-V_{1}).\]

(74)

Мысалы, цилиндрдің ішінде ілгерілемелі еркін қозғалатын поршечь мен цилиндрдің арасындағы газ қыздырудың немесе суынудың нәтижесінде изобаралық жұмыс жасайды. Термодинамиканың бірінші бастамасын ескеріп:

20 - сурет.

\[d Q=c_{\nu}d T+p d V,\]

мұндағы с _v изохоралық жылу сыйымдылығы. Сонымен, изобаралық процесс кезінде газға берілген жылу мөлшері оның ішкі энергиясын арттыруға және сыртқы күштерге қарсы істелген жұмысқа жұмсалады. Изобаралық жылу сыйымдылық:

\[c_{p}=d Q/d T,d Q=c_{p}d T\]

Енді dQ, мәнін орнына қойып (75) теңдеуді

\[{\cal C}_{p}d T={\cal c}_{\nu}d T+p d U\]

(76)

түрінде жазуға да болады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.