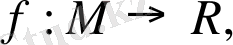Тегіс көпбейнеліктер: бірліктердің бөлінуі, тасымалдаушы функциялар және жанама кеңістігі


Бірліктің бөлшектенуі.
Айталық, М- тегіс көпбейнелік.
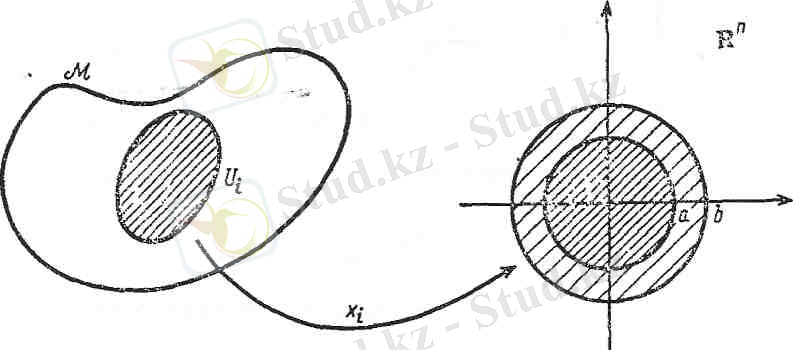 М көпбейнелігінде берілген
М көпбейнелігінде берілген
функциясының тасымалдаушысы деп
f(p)
 0
болатын, М-дегі
р
нүктелер жиынының тұйықталуын айтамыз.
0
болатын, М-дегі
р
нүктелер жиынының тұйықталуын айтамыз.
Б е л г і л е у: supp f. Мысал 1.
R 1 түзуінде берілген
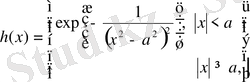
21-сурет
Бұл функциясының барлық ретті үзіліссіз дербес туынды табылады (R 1 - де тегіс болып табылады), оның тасымалдаушысы [-а, а] кесіндісімен сәйкес келеді.
- а а
Сурет 21. Шексіз дифференциалданатын ақырлы функция
Сурет 22. Біріне бірі жамылған жиындар осылай орналасқан және функция сақталады, олар жеке бөліктерден тұрады.
Мысал 2. Алдыңғы мысалды қолдана отырып, R n кеңістігінде тегіс g:
R функциясын құру қиын емес, тасымалдаушы supp g n-өлшем жабық шарымен сәйкес келеді.
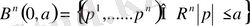
Орнына қою жеткілікті
g(x 1 , . . . x n ) =h((x 1 ) 2 +…. +(x n ) 2 ) .
{Ui} -M көпбейнелігінде ашық тұйықталған болсын .
Анықтама. Тегіс функцияның құрылымдары
(тегіс) бiрлiктер бөлiктеу деп аталады, тұйыққа бағынатын {Ui}, егер ол келесі қасиеттерге ие болса:
- 0 барлықрүшін M-нен және кез-келгенiүшін.
- кез-келгенIүшін;
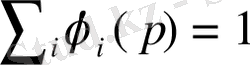 i
i
ТЕОРЕМА 1.
 - тегіс көпбейнелік және U=
- тегіс көпбейнелік және U=
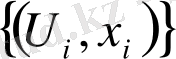 -
-
 атласынан алынған болсын
.
Сонда тегіс бірліктерді бөліктейтін болып табылады, тұйыққа бағынатын
{Ui}
(сурет 22) . Кездейсоқ үшін тексеріп көреміз, сонда
атласынан алынған болсын
.
Сонда тегіс бірліктерді бөліктейтін болып табылады, тұйыққа бағынатын
{Ui}
(сурет 22) . Кездейсоқ үшін тексеріп көреміз, сонда
 жинақты (компактно) . Сол себепті, U атласы ақырлы санды картадан құралған деп есептейміз. Және
U
дан алдынған кез келген
(U
i
, x
i
)
картасы үшін жиын
жинақты (компактно) . Сол себепті, U атласы ақырлы санды картадан құралған деп есептейміз. Және
U
дан алдынған кез келген
(U
i
, x
i
)
картасы үшін жиын
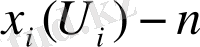 - өлшемді ашық шар
В
п
(0, b
)
центрі
О
нүктесінде жатады және радиусы
b.
- өлшемді ашық шар
В
п
(0, b
)
центрі
О
нүктесінде жатады және радиусы
b.
а<b
деп аламыз,
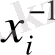 (В
п
(0, а) )
жиыны мен
(В
п
(0, а) )
жиыны мен
 жабық болсын. (сурет 23)
жабық болсын. (сурет 23)
Сурет 23. Бiрлiктiң бөлiктеуiн бiр элементтiң құрастыруы
Қоямыз
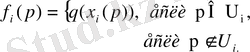
Функция f i (p) төмендегідей қасиеттерге ие;
1) 0
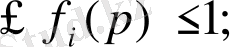
2)
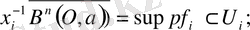
3)
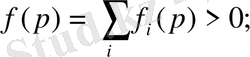
4)
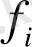 - M көпбейнелілігіндегі тегіс функция
.
- M көпбейнелілігіндегі тегіс функция
.
Сондықтан функция
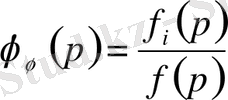 қажетті бөліктерге ие.
қажетті бөліктерге ие.
Дифференциал- жанама кеңістіктердің арасындағы тегіс бейнелеуі ретінде.
M және
N
- тегіс көпбейнелік және
f:
 - тегіс бейне болсын. Келесі жолы М нен алынған р - нүктесі және
q=f(p)
-оған үйлесімді N нен алынған бейнеге сәйкес нүкте.
Т
Р
M
және
T
q
N
қатысты кеңістіктерді қарастырамыз
.
Әрбір жанама
- тегіс бейне болсын. Келесі жолы М нен алынған р - нүктесі және
q=f(p)
-оған үйлесімді N нен алынған бейнеге сәйкес нүкте.
Т
Р
M
және
T
q
N
қатысты кеңістіктерді қарастырамыз
.
Әрбір жанама
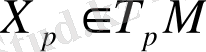 векторын сәйкес
Y
векторын сәйкес
Y
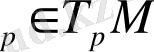 жанама векторына төмендегі шарттары бойынша сәйкес етіп қоямыз.
жанама векторына төмендегі шарттары бойынша сәйкес етіп қоямыз.
Мұндағы
g
 C°°(q)
-еркін тегіс функция.
C°°(q)
-еркін тегіс функция.
Y
q
,
анықталатын байланыс (1), шындығында
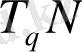 - дегі қатысты вектор болып табылатындығын көрсетеміз
.
- дегі қатысты вектор болып табылатындығын көрсетеміз
.
g, h
 C°°(q),
C°°(q),
 R болсын. Сонда
R болсын. Сонда
1.
(g + h) =X p ((g + h)
f) =X P( g
f + h
f) =
= X P (g
f) + X
(h
n=Y g (g) + Y q (h) .
- Yg(g) = Xp((ag) f) =Xp((gf) ) =Xp(gf) ==Yq(g) .
- Yg(g. h) = X(ghf) = X(gf) . (hf) ) = = Xp(gf) . (hf) (p) + (gf) (p) . Xp{hf) = =Y(g) +h{q) +Yp(h) .
Дәл осылай T q N қатысты кеңістігінде Т Р M бейнелі қатысты кеңістігі құралған.
{df) p = f. p :T p M
T q N
f
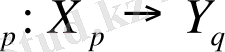
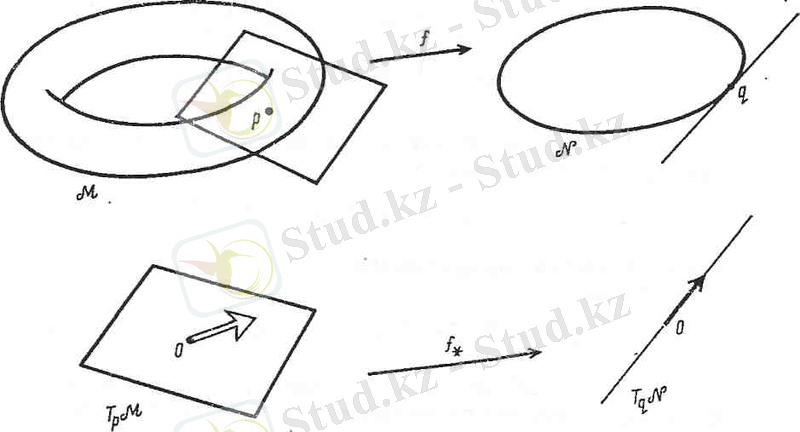
Бұл бейнелер - бейнелер дифференциалы және қатысты бейнелер деп аталады (сурет 29) .
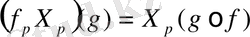
Сурет 29. Қатысты бейнелер
Дифференциалдық жүйе.
Жанама вектордың сызықтық оператор түрінде анықталуы.
Тегіс көпбейнеліктің кеңістігінде жанама вектор құру үшін негізге R n координаталық кеңістігінің нүктесінде берілген векторлар арасындағы байланысты және осы кеңістіктегі функциялардан бағыт бойынша туындыны есептеу амалдарын алуға болады.
Айталық
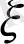 P
- p
P
- p
 R
n
нүктесінде берілген R
n
координаталық кеңістіктің векторы болған. Онда
р
нүктесінің аймағында анықталған кез келген
R
n
нүктесінде берілген R
n
координаталық кеңістіктің векторы болған. Онда
р
нүктесінің аймағында анықталған кез келген
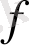 тегіс функциясы үшін
тегіс функциясы үшін
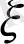 P
векторымен берілген бағыт бойынша туындысы табылады. (25 сурет) .
P
векторымен берілген бағыт бойынша туындысы табылады. (25 сурет) .
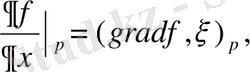 немесе координатада
немесе координатада
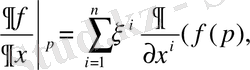
Осыны
р
нүктесінде
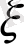 векторы бойынша
f
функциясының туындысы деп атаймыз және
векторы бойынша
f
функциясының туындысы деп атаймыз және
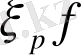 арқылы белгілейміз.
арқылы белгілейміз.

 25 сурет
25 сурет
Сонымен, р нүктесінің аймағында С°°(р) тегіс функциялар жиынында берілген векторлар бойынша келесі операция орындалады.
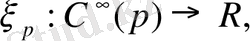
Жоғарыдағы ереже бойынша
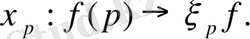
Бұл операция келесі қасиеттерді қанағаттандырады:
1.
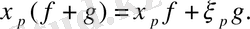
2.
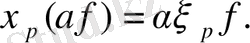
3.
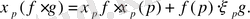
(мұнда f және g - С ºº (р) жиынында кез келген функциялар а - сандар) .
Ескерту: келесі фактті көрсетейік. Айталық,
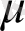 :C°°(p)
:C°°(p)
 R
төмендегі шарттарға тәуелді кейбір бейнелеу:
R
төмендегі шарттарға тәуелді кейбір бейнелеу:
1.
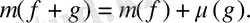
2.
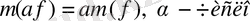
3.
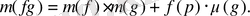
Онда
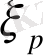
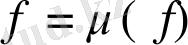 орындалатындай тек бір ғана
орындалатындай тек бір ғана
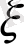 векторы табылады.
векторы табылады.
Анықтама: М көпбейнелігі р нүктесінде жанама векторы деп С ºº ( р ) жиынындағы әрбір f функциясына X p f санын сәйкес қоятын
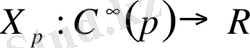
ережесін айтамы және бұл ереже келесі қасиеттерге ие:
1. X p (f + g) = X p f + X p g.
2. X p {af) = aXf.
3. X p (f. g) = X p f. g(p) + f(p) . X p (g)
{мұндағы f, g
C°°(p),
R) .
Айталық, Х р - жанама вектор,
R - кез келген сан.
Х р (а) = 0. *
болатындығын көрсетеміз.
Х
Р
(1) = Х
Р
(1
 ) = Х
Р
(1) . 1 + 1. Х
Р
(1) -2Х
Р
(1)
) = Х
Р
(1) . 1 + 1. Х
Р
(1) -2Х
Р
(1)
Қатынасынан Х р (1) =0 орындалатындығын көреміз. Бұдан
X
p
(
 ) = X
p
(
) = X
p
(
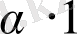 ) =
) =
 X
p
(l) =
X
p
(l) =
 0 = 0. *
0 = 0. *
Жанама кеңістіктің өлшемі және базисі.
Теореманың дәлелдеуі.
Алдымен
 ,
,
жанама векторы барлық Т Р М. к еңістігін туындайды.
Айталық,
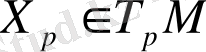 . Жалпы алынған (U
х)
локальді картасы келесі қасиеттерге ие :
. Жалпы алынған (U
х)
локальді картасы келесі қасиеттерге ие :
- i=l, . . . , n;
- x(U), - Rn. -де ашық шар.
(1) формулада ф-ті f°x -1 , арқылы алмастырып, алатынымыз
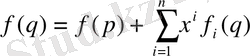
Мұндағы q - U - дағы кез елген нүкте және
.
X p f. есептеуге көшеміз. Алатынымыз
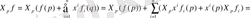
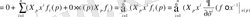
Жоғарыдан шығатыны
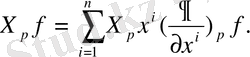
Осыдан f
C°°(p) функциясы кез келген функция болғандықтан
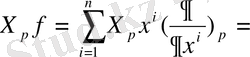
(3)
Енді
векторлары сызықты тәуелді емес екендігін көрсетеміз
Айталық
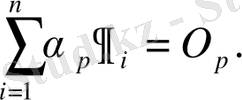
онда
Бірақ
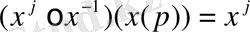 және
және
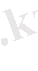
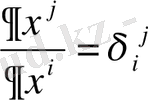
Сондықтан
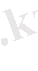
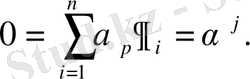
Сонымен
 - базис Т
р
. М.
жан. кең. базисі болып табылады.
- базис Т
р
. М.
жан. кең. базисі болып табылады.
СЛЕДСТВИЕ. dimзT p M=dimM.
Басқа
(V, у), p
 ,
локальды картасын таңдай отырып, жанама кеңістігінің келесі
,
локальды картасын таңдай отырып, жанама кеңістігінің келесі
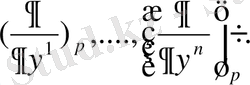 базисін аламыз
базисін аламыз
Бұл базистің векторларын
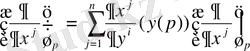 формуласы арқылы
формуласы арқылы
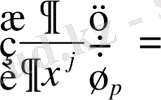 1, . . . , n, базисінің векторлары арқылы сипаттауға болады.
1, . . . , n, базисінің векторлары арқылы сипаттауға болады.
Айталық f
 C°°(p), онда
C°°(p), онда
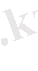
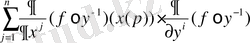
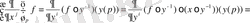
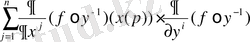
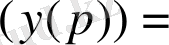
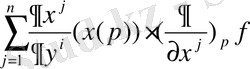
Осыдан, f кез келген функция болғандықтан (4) формуланы аламыз. *
Сонымен қатар (4) формуланы (3) бағалаудан
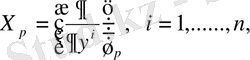
орындалатынын біле отырып алуымызға болады.
Ескерту 1. Айталық M = R n және
T p R n . Онда R n -де
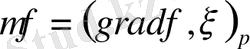
орындалатындай тек бір ғана
векторы табылады. *
R n кеңістігінде (U, x) канондық координаттар жүйесіне таңдап аламыз:
U=R n , x=
Онда
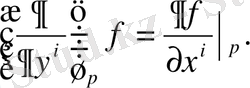
(2) формулаға
=X p , қоя отырып
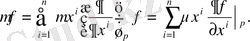
Белгілеу енгіземіз
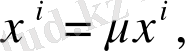
Қажет формулаға көшеміз:
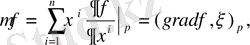
мұнда
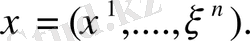
Ескерту 2. Қатысты кеңістіктер Т p , M және
, мұндағы
, ортақ элементтері жоқ. Бөлшектерден құралған,
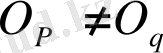
Көпбейнелерде анықталған тегіс функциялар.
Айталық М тегіс көпбейнелілігінде
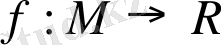 , функциясы берілсін, яғни М көпбейнелілігінде әрбір
р
нүктесіне белгілі бір ереже бойынша
u=f (p),
саны сәйкес қойылады.
, функциясы берілсін, яғни М көпбейнелілігінде әрбір
р
нүктесіне белгілі бір ереже бойынша
u=f (p),
саны сәйкес қойылады.
Айталық р - берілген нүкте болсын.
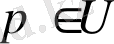 болғандай (U,
х)
жергілікті картасын аламыз. Онда берілген
f(p)
функциясын, анықталу облысы R
n
координаталық кеңістігінде
x(U)
ашық картасы болып табылатын қарапайым
п
айнымалыдан туратын
х
1
, . ., ., х
п
функциясымен байланыстыруға болады.
болғандай (U,
х)
жергілікті картасын аламыз. Онда берілген
f(p)
функциясын, анықталу облысы R
n
координаталық кеңістігінде
x(U)
ашық картасы болып табылатын қарапайым
п
айнымалыдан туратын
х
1
, . ., ., х
п
функциясымен байланыстыруға болады.
Бұл функция келесі ережелерге сәйкес құрылады:
где

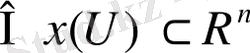
(сурет. 20) . R
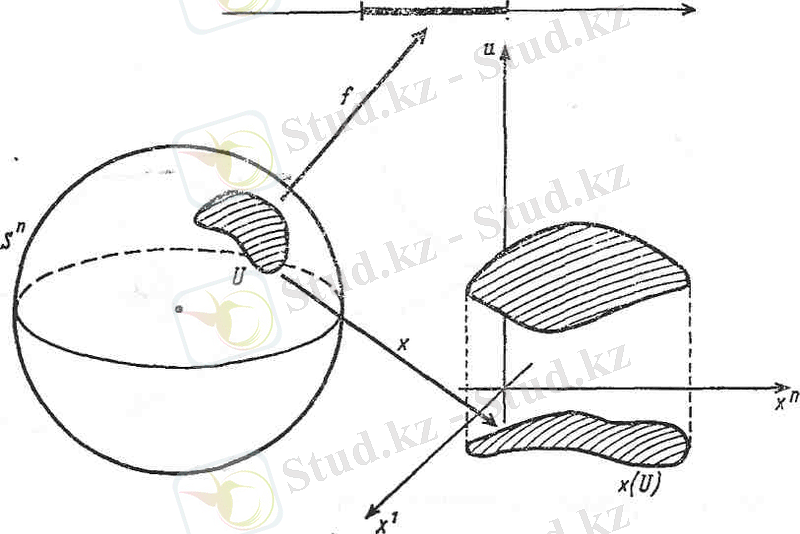
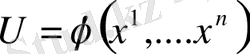
R
Сурет . 20. Сферадағы жергілікті координатада көрсетілген функцияның графигі
Пайда болған функция {U, х) жергілікті картасына тәуелді .
Айталық,
(V, у), p
 V,
- келесі жергілікті картасы болсын.
V,
- келесі жергілікті картасы болсын.
Жоғарыдағы ережеге сәйкес:
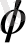
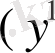 , . . . , y
n
)
, . . . , y
n
)
 )
)
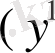 , . . . , y
n
)
где
(у
1
. . . ,
y
n
)
, . . . , y
n
)
где
(у
1
. . . ,
y
n
)
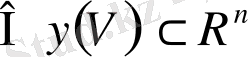 функциясын аламыз
.
функциясын аламыз
.
Егер
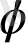 функцияның R
n
кеңістігіндегі
x(U)
ашық облысына барлық үзіліссіз дербес туындысы бар болса яғни
функцияның R
n
кеңістігіндегі
x(U)
ашық облысына барлық үзіліссіз дербес туындысы бар болса яғни
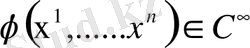 , онда функциясы кеңістігінің облысында санатына жатады
С°°.
, онда функциясы кеңістігінің облысында санатына жатады
С°°.
Орындалатынын көреміз:
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz