Геодезиялық торлардың классификациясы және негізгі геодезиялық әдістері


Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 33 бет
Таңдаулыға:
ГЕОДЕЗИЯЛЫҚ ТОРЛАРДЫҢ КЛАССИФИКАЦИЯСЫ
Мазмұны
I. Пландық геодезиялық торлардың классификациясы
1. 1 Геодезиялық тор
Геодезиялық тор деп - координаталары мен биіктіктері анықталған жер бетінде бекітілген нүктелер жүйесі аталады. Геодезиялық торлар үлкен және кіші аймақтарда құрылады, сонедықтан оларды келесі түрлерге жіктеуге болады:
1) глобальды геодезиялық тор
2) мемлекеттік геодзиялық тор
3) жиілету торлары
4) геодезиялық түсіру торлары
Геометриялық түрі бойынша геодезиялық торларды пландық , биіктік және кеңістік торларға бөледі.
Торды құрғанда «жалпыдан жекеге ауысу» принципі қолданылады. Глобальды геодезиялық тор ғарыштық геодезия әдістері арқылы жобаланады. Пункттердің орналасу жағдайы тік бұрышты геоцентриялық жүйеде анықталады. Бұл жүйенің басы жердің салмақ орталығымен бірлескен Z осьі ретінде жердің айналу осьі алынған. Ал, ZY жазықтығы ретінде бастапқы меридианның жазықтығы алынған. Глобальды геодезиялық торды жоғарғы геодезияда, геодинамикада, астрономияда және басқа да ғылымдардың ғылыми және ғылыми-техникалық мәселерін шешуге қолданылады. Осындай мәселелерге мыналар жатады:
1) фундаментальды геодезияның тұрақты шамалары,
2) жердің гравиметрияялық аясын және фигурасын зерттеу,
3) жер бетінің деформациясын, жылжуын зерттеу (литосфералық қабаттар)
Мемлекеттік геодезиялық тор деп мемлекеттің территориясында координаталардың таралуын қамтамасыз ететін және басқа да геодезиялық торларды құруға негіз бола алатын геодезиялық торды айтады.
Мемлекеттік геодезиялық тордың пландық жағдайы жалпылама мемелекеттік координаталық жүйеде, ал биіктіктер бірегей мемлекеттік жүйеде анықталады.
Мемлекеттік геодезиялық торлар 3 түрге бөлінеді:
1) мемлекеттік геодезиялық тор (пландық)
2) нивелирлік тор (биіктік)
3) мемлекеттік гравиметриялық тор.
Пландық геодезиялық торларды негізінен триангуляция , трилатерация , полигонометрия , сонымен қатар осы әдістердің аралас әдістерімен құрады.
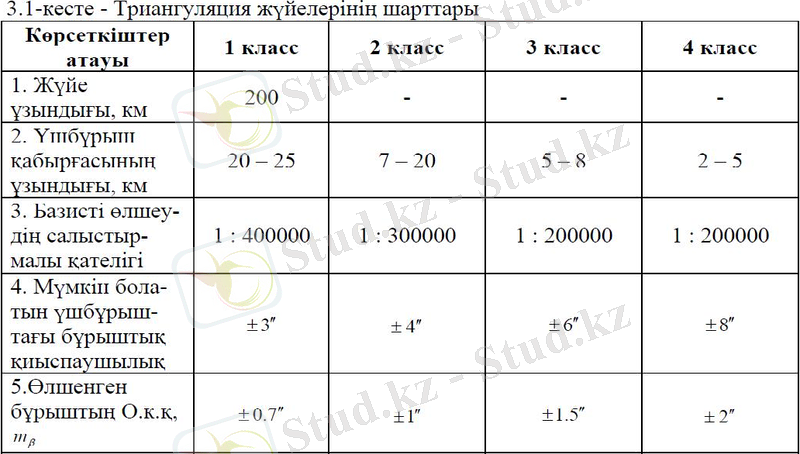 Мемлекеттік пландық геодезиялық тор триангуляция, трилатерация және полигонометрия әдістерінен құрылып 1, 2, 3, 4 класқа бөлінеді де, бір-бірінен бұрыштарды және ұзындықтарды өлшеу дәлдігімен, үшбұрыштардың өлшемдері, жүріс ұзындықтары және оларды құру ретімен ерекшеленеді.
Мемлекеттік пландық геодезиялық тор триангуляция, трилатерация және полигонометрия әдістерінен құрылып 1, 2, 3, 4 класқа бөлінеді де, бір-бірінен бұрыштарды және ұзындықтарды өлшеу дәлдігімен, үшбұрыштардың өлшемдері, жүріс ұзындықтары және оларды құру ретімен ерекшеленеді.
1. 1 -кесте. Мемлекеттік триангуляциялық торлар
Жердің физикалық бетінде орналасқан, геодезиялық пункттар орны үш координат бойынша анықталады; В ендігімен, референц-эллипсоид бетіндегі L бойлығымен және пункттің эллипсоид бетімен, Н биіктігімен. В және L координаталары пункттың пландық орнын анықтайды. Тәжірибелік мақсаттар үшін пункттің пландық орнын жазықтықта х және у координаталарымен, мысалы Гаусс проекциясында анықтайды. Н биіктігі оның геоид бетінен биіктік шамасының және геоидтың эллипсоидтан алшақтау шамасының қосынды ретінде келтіреді. Жер бетінде пункттардың өзара орнын анықтаудың жалпы принципі келесідей. Жергілікті жерде бір-бірімен байланысқан геометриялық фигураларды, әдетте үшбұрыштарды, орналастырады. Бұл фигуралардың төбелерін, олардың кейбір элементтері үздіксіз өлшеулер үшін ыңғайлы болатындай етіп таңдайды.
Үшбұрыштағы пункттардың пландық орнын анықтау үшін, мысалы, бір қабырғасын және екі бұрышты немесе екі қабырғасын және бір бұрышын өлшеу жеткілікті, қалған элементтерің аналитикалық түрде оңай есептеп шығаруға болады. Бірақ геодезиялық жұмыстар тәжірибесінде, геометриялық құрылыстардың барлық элементтерін анықтауға қажетті өлшеулерден көп орындайды. Артық өлшеулерді геодезиялық торлар құрудың сапасын жоғарлату үшін, тексеру үшін және дәлдігін бағалау үшін жасайды.
Фигуралар төбесінің абсолютті биіктіктерін анықтау мақсатымен, не қабырғалар ұзындығын біле отыра вертикаль бұрыштарды өлшеу жолымен, не геометриялық нивелирлеу жолымен, сәйкес өсімшелерді (биіктіктер айырмашылығы) анықтайды, көршілес пункттердің биіктіктерінің айырмашылығын анықтайды.
Бірақ құрылған фигураларды бағдарлау, пландық орнын анықтау және барлық төбелердің биіктіктерін анықтау үшін бір қабырғаның азимутын (дирекциондық бұрышын), координаттарын ( В, L немесе х және у ) және фигуралар жүйесінің бір төбесінің абсолюттік биіктігін білу қажет. Пландық орынды анықтау және пункттердің биіктік қалпын анықтау тәсілдерінің бір-бірінен едәуір айырмашылығы бар екендігін есепке алу керек. Пландық орнынды анықтау және геодезиялық пукттердің биіктіктерін анықтау өлшеулері бөлек және көбінесе әр түрлі тіктеуіштермен жасалады.
Осылай тірек торын құрып, оның пункттарына қатысты жергілікті жердің кез-келген нүктесінің орын анықтауға болады. Өлшеулер түріне байланысты геодезиялық тор триангуляция, трилатерация, полигонометрия және олардың аралас тәсілдерінен құрылады. Соңғы кезде бір-бірінен алшақ жатқан пункттер орнын Жердің жасанды серіктерін бақылау арқылы анықтайтын болды.
II. Триангуляция
2. 1 Триангуляция туралы жалпы мағлұмат, I, II, III, IV класс триангуляциясының сипаттамасы
Триангуляция - бұл жергілікті жерде, горизонтальді бұрыштарды және бір үшбұрыштың қабырғасының ұзындығы (қабырғалар бірнеше үшбұрышта өлшенуі мүмкін) анықталатын, бір біріне ұласқан үшбұрыштарды құру. Үшбұрыштарды өлшенген b қабырғасынан, бастапқысына қатысты біртіндеп шеше отырып (1. 1-сурет), үшбұрыштар жүйесінің барлық қабырғаларын анықтайды. Жергілікті жерде бекітілген және сәйкес белгіленген үшбұрыштар төбелері триангуляция пункттары деп аталады. Триангуляцияның өлшенген жағы базисті деп аталады, ал координаталары берілетін пункт триангуляцияның бастапқы пункты деп аталады.
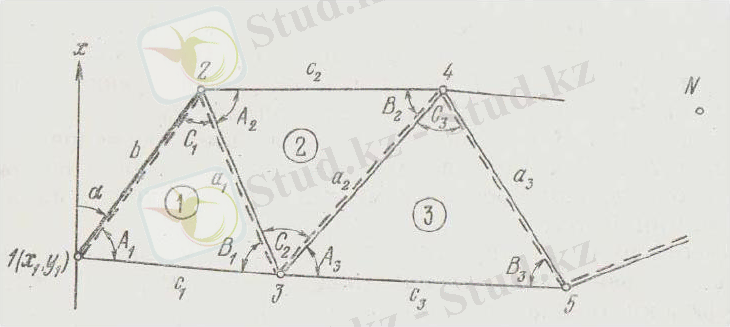
1. 1 -сурет. Триангуляция үшбұрыштар қатары
Триангуляцияның жағын өлшеу мүмкін болмаған кейбір жағдайларда жергілікті жерде базистік тор құрылады (1. 2-сурет) . Шығыс жағы деп аталатын (1-2-3) торы үшбұрышының 1-2 жағының ұзындығы базистік торды өңдеуден аналитикалық түрде анықталады. Базистік тор әдетте кіші АВ диагоналі немесе кіші қабырғасы өлшенетін ромб түрінде болады.
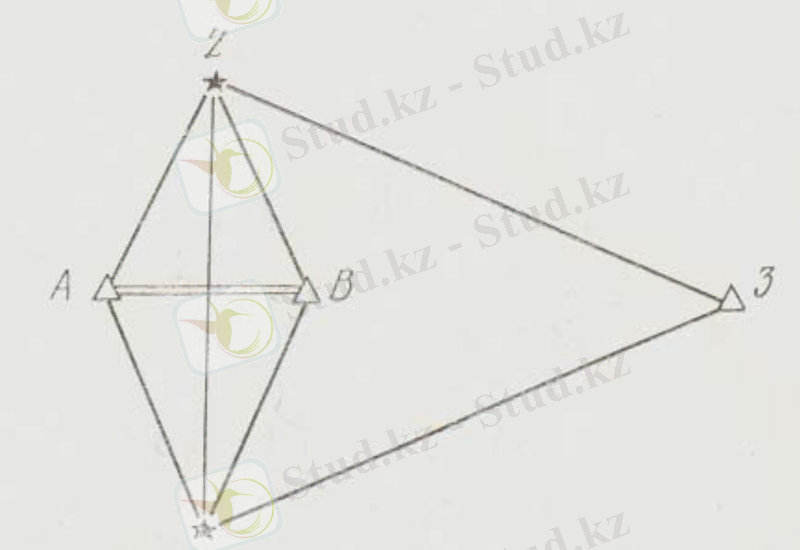
1. 2 -сурет. Базистік тор
2. 2 Бірінші кластың триангуляциясы торы
Мемлекеттік триангуляция жүйелерін 1, 2, 3, 4 кластарға бөледі.
1 класс - астрономды геодезиялық, Жердің өлшемі мен пішінін анықтаумен байланысты ғылыми мәселелерді шешуге арналған. Сонымен қатар 1 кластың триангуляция жүйелері төменгі класты триангуляциондық жүйелерді дамыту үшін негізгі болып табылады. 1 кластың триангуляциясының үлкен аймақтарында меридиандар мен параллельдер бағытында орналасқан және бір бірінен 200 км артық емес қашықтыққа алыстаған үшбұрыштар тізбегі ретінде жасалады. Триангуляция тізбектері өзара қиылысып периметрі 800 км артық емес полигондарды түзеді. Үшбұрыштардың қабырғалары пішіні бойынша теңқабырғалыларға жақын болуы керек. Түйіннің ұштарында А, В, С, D нүктелерінде базистік қабырғалар беріледі (қабырғаның ұзындығын өлшейді) . Көлденең бұрыштарды өлшегеннен кейін 1 класс триангуляциясында гравиметриялық түсірілімді жүргіземіз.
2. 3 Екінші және төменгі класс торлар жүйесі
Бұл жұмыс 1 кластық жүйенің әр полигонында орындалады. 2 кластың триангуляциясы 1 класс полигонының толық ауданын толтыратын және контур бойында бірінші кластың тірек пункттерімен сенімді байланысқан үшбұрыштардың тұтас жүйесі ретінде дамиды. Екінші кластық жүйесінің ортасында бір EF базистік қабырғасы беріледі, онда астрономиялық координаттардың анықталуы жүргізіледі. 2 кластың триангуляциясының үшбұрыштарының қабырғалары 7 ден 20 км дейін болуы мүмкін. 2 кластық триангуляциясында барлық бұрыштарды өлшейді және 1 класс триангуляциясына сәйкес теңестіреді. 3 және 4 класс триангуляцияларының тірек пункттері жоғары кластар тірек пункттерімен байланысты анықталады, негізгі пункттерді немесе жеке пункттерді салу. 3 класс триангуляциясын өзара жеке 1 және 2 класты кірістірмей теңгереді. 4 класс триангуляциясын жоғары класс үшбұрышына тура немесе кері таңбамен тіректіі қосумен салады2, 3, 4 кластар триангуляциялары топографиялық түсірілімдердің дамуы үшін тіреуіш жүйе болып табылады. 1 : 5 - 1 : 5000 масштабты түсірілімдерді қамтамасыз ету үшін біріктіру жүйелері жүргізіледі, оларға I, II дәрежелі триангуляциялар және I, II дәрежелі полигонометрия жатады. 1 : 2000 - 1 : 500 масштабтары үшін салынбалы жүйелер қызмет етеді. 1 класс триангуляциясының бекеттеріне 2 класс триангуляциясының бекеттерінің байланысу сызбасы үшбұрышпен, төртбұрышпен және желпеуішпен жүзеге асырылады.
2. 4 Триангуляциондық жүйенің жобасын құрудың жалпы мәліметтері
Триангуляция жүйесін жобалау құрамына кіретіндер:
1. Алдында дамытылған жүйелерді аса толық мөлшерде қолдану үшін жұмыс аймағының геодезиялық зерттелуінің талдауы;
2. Жүйенің жобалау сызбасын картада бекеттердің ыңғайлы орналасуын және жобаның техникалық тапсырмасына сәйкес олардың қажетті бірлесуін жасауды ескерумен құрастыру;
3. Триангуляция бекеттерінде белгілердің биіктігінің алдын ала есебі;
4. Қолда бар нұсқаулықтар бойынша жұмыс әдістемесін, техникалық шектерді белгілеу, триангуляционды жүйенің элементтерінің болжамды нақтылығының алдын ала есебі;
5. Жұмыстың жалпы көлемін және қажетті құралдарды (кадрлар, көлік, саймандар, материалдар) белгілеу.
Техникалық жобалау алдында орындалған геодезиялық жұмыстар бойынша мәліметтер жинаудан басталады. Іс жүзінде бар триангуляция тірек пункттерін және олардың тұрғызылу сызбасын жобаның топографиялық картасына түсіреді. Егер бастапқы болып табылатын пункттердің сақталуы туралы күмән болса бекеттердің сақталуын зерттеу мақсатында рекогносцировка жүргізу қажет. 1, 2 класс триангуляциясының жүйелерінің жобасын құрастыру 1 : 1 масштабты топографиялық карталарда, ал 3, 4 кластары 1 : 15, 1 : 25000, 1 : 1 масштабты карталарда орындалады.
2. 5 Айналдыру тәсілімен өлшенген бағыттың теңдеуі және оның дәлдігі (Струве тәсілі)
Мысалы: P пунктінде n бағытымен 1, 2, 3, . . . n пункттерін айналма тәсілімен өлшеу керек болсын дейік.
Ол үшін лимбті бекітіп, алтдаданы сағат тілі бағытымен дүрбіні ДС қалпында 1, 2, 3, . . . n пункттеріне кезектеп нысаналайды, қайтадан 1 пунктіне нысаналап, n+1-ге көздейді де есепті лимб бойынша алады. Бұл бірінші жарты айналым болады.
Содан дүрбіні зенит арқылы айналдырып, лимб сол қалпында, ал алидада айналымы сағат тілі бағытына қарсы болғанда, дүрбіні 1, n, n-1, …3, 2, 1 пункттеріне кезектеп көздеп, n+1 нысаналайды да, лимбтан есеп алады: . Бұл өлшенгендердің бәрі 2-ші жарты айналым, ал екі жарты айналым толық айналма әдісін құрайды.
1-ші пунктіне бағытталған бағыт, екі рет қарастырылады. Оны бастапқы бағыт деп атайды және оны әдетте жақсы көрінісі бар жерде тандайды.
Толық айналма әдіспен өлшенген бағыттарды өңдеу, ДС және ДО өлшенген аттас есептердің орташа арифметикалық мәнін есептеуден басталады.
A111=1/2(Li+Ri) .
Нәтижесінде A1, A2, A3 … An, A, «есеп» қатары пайда болады, олар арасында 1 пунктінде өлшенген қателігі пайда болады.
.
қателікті есептеу үшін, түзетпені бүкіл бағыттарға ендіру керек.
.
Бұдан бағыттардың тұрақты мәнін есептегеннен соң, M1=0, M2…
Mi=(Ai+бi) -A1.
1961 жылға дейін СССР бойынша арқылы бастапқы бағытты өлшеу ғана болды, бұдан
,
Mi=A1- 1.
Бұл қателіктерді өлшеу, яғни қателіктерді толық жою болып табылады. Олар аспаптан, қоршаған ортаның әсерінен пайда болады. Лимб бөлінділерінің қателігін болдырмау үшін, есепті лимб доғасына тегіс және олар лимбтің әр бөлшектеріне тиетіндей етіп орындалады. Ол үшін лимбті әр айналым сайын 180/m+б бұрышына қояды, m - айналым саны. - микроскоп микрометрлік теодолиттер үшін, - оптикалық теодолиттер үшін.
Бағыттың дәлдігін есептеу, жеке айналым бағытынан оның орташа арифметикалық қосындысының ауытқуына тең. Практикада Петерс формуласын қолданады.
.
«m» айналыммен өлшенген о. к. қ. бағыты мынаған тең:
M = ,
мұндағы, n - пунктқа бағытталған амалдар саны;
m - айналым саны;
U - жеке айналым бағытынан орташа арифметикалық қосындысының ауытқуы.
«K» мәні айналым амалдарының санына байланысты:
= 0, 15;
Бір тәсілмен өлшенген бағыттың ОКҚ
мұндағы: К - 4 класс триангуляциясы ушін коэффициент, К = 0, 23;
n - бағыт саны;
n приеммен өлшенген бұрыштың ОКҚ:
M =
Бөлек бұрыштың өлшеінің қателігі:
2. 6 Триангуляция жүйесінің қабырға ұзындықтарының қателі-гін алдын ала есептеу
Әдетте алшақ қабырғаның ұзындығының қателігін жүйенің қажетті нақтылығының қанағаттануын анықтау үшін алдын ала есептейді. Қателік өлшемдер, жүйе конструкцияларының және үшбұрыштардың пішіндерінің дәлдігімен анықталады. Аса әлсіз қабырғаны анықтау кезінде екі факторды ескеру қажет:
1. Қабырғаның бастапқыдан алыстау дәрежесін;
2. Осы қабырғаның басқа қабырғалармен салыстырғандағы ұзындығын.
Басқа тез жағдайларда қабырға қанша қысқа болса, соншалықты оның салыстырмалы қателігі көп болады.
Дәлдіктің алдын ала есебін жүйенің әр түрлері үшін есептейді:
1. Егер А және К нүктелерінің координаталары белгілі болса, онда жүйе қатты деп аталады;
2. Егер соңғы бекеттің координаттары белгісіз болса, онда жүйе бос деп
 аталады.
аталады.
1. 3 -сурет. Бастапқы (базистік) қабырға
АВ - бастапқы (базисная) қабырға;
а қабырғалар - байланыстыру қабырғалары;
с қабырғалар - аралық қабырғалар.
Үшбұрыштар тізбегінің соңғы қабырғасы
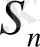 алшақ қабырға деп аталады. Бос тізбекте үш шарт қанағаттандырылуы керек:
алшақ қабырға деп аталады. Бос тізбекте үш шарт қанағаттандырылуы керек:
1.
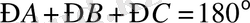 - фигураның (үшбұрыштың) шарты (2. 1)
- фигураның (үшбұрыштың) шарты (2. 1)
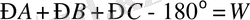 - үйлеспеушілік (2. 2)
- үйлеспеушілік (2. 2)
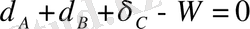 (2. 3)
(2. 3)
2. Базистік шарттар
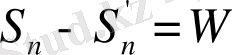
(2. 4)
мұндағы
 - есептеп шығарылған ұзындық;
- есептеп шығарылған ұзындық;
3. Дирекциондық бұрыш немесе азимут шарты, егер бастапқы және соңғы дирекциондық бұрыштар белгілі болса.
Егер жүйе бос емес яғни, қатты болса, онда X, Y координаталарының шарты және қатты бұрыш шарты пайда болады.
 1. 4 -сурет. Орталық жүйе
1. 4 -сурет. Орталық жүйе
Нақтылықты алдын ала есептеу жүйе элементтерінің орташа квадраттық қателіктерін анықтаудан тұрады:
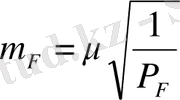
(2. 5)
,
мұндағы
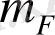 - о. к. қ. функциялар;
- о. к. қ. функциялар;
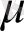 - салмақ о. к. қ. ;
- салмақ о. к. қ. ;
P F - салмақ.
Бұрыштар үшін
 (бұрыштық о. к. қ. ) . Бастапқы мәліметтердің қателігін ескерумен мынаны жазамыз:
(бұрыштық о. к. қ. ) . Бастапқы мәліметтердің қателігін ескерумен мынаны жазамыз:
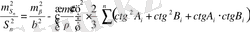
(2. 6)
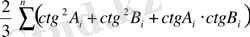
(2. 7)
- жүйенің геометриялық шарты немесе кері салмақ деп аталады.
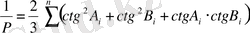
(2. 8)
Тәжірибеде котангенстер синус бұрышының логарифмінің 1 секундқа өзгеру шамасына алмастырылған формулалар қолданылады.
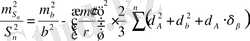
(2. 9)
2. 6 Триангуляция пункттерінің рекогносцировкасы
Рекогносцировканың басты мақсаты жобаланған пункттердің орналасуын нақты таңдау және геодезиялық белгілердің биіктігін анықтау болып табылады. Рекогносцировка кезінде елді - мекендердің жерінің сипаты, жол және гидрографиялық жүйе, топырақ, құрылыс материалдарының болуы жайлы мәліметтер жинау жүргізіледі.
Рекогносцировка негізінде жобаға қосымшалар мен толықтырулар енгізіледі. Пункттерді салу орнын таңдау кезінде пункттерді басты биіктіктерде, жер бетінің тау жұмыстары әсерінен ығысуынан тыс аймақта орнықты топырақта центрлердің және сыртқы белгілердің ұзақ уақыттық сақтаулығы орындалатындай етіп орналастыру қажет. Пункттерді темір жолдан және автокөлік жолынан, телефон және телеграф желісінен белгінің екі еселі биіктігінен жақын емес қашықтықта және жоғары кернеулі электр желілерінен 120 м аз емес қашықтықта салу керек.
Жергілікті жерде бекеттердің салыну орындары жерге жер қорғандарымен немесе тастардан үйілетін турлармен көмілетін белгілермен, бағаналармен белгіленеді. Пункттердің атауы топографиялық картада қабылданған транскрипцияны сақтаумен жақындағы елді - мекеннің атымен сәйкес келуі керек. Егер жобаланған пункт іс жүзінде бар триангуляциямен немесе талдау жүйесімен сәйкес келсе, онда центрдің дәл бірлесуін қарастыру қажет. Іс жүзінде бар центрлерге тікелей жақын арада жаңа центрлердің салынуына жол бермеу керек.
Егер қандай да бір себептермен жаңа триангуляция пункті алдында дамытылған жүйенің пунктімен бірлеспесе, онда ескі пункт орталығын жояды (рұқсат алғаннан кейін) .
Рекогносцировка жұмыстарының күрделілігі және әдістері жердің жағдайларына және триангуляция класына тәуелді болады. Белгілердің қабылданған биіктігі кезінде пункттердің арасындағы көру мүмкіндігінің болуы теодолиттің көтерілу биіктігіне тез биіктіктен елді мекенді тікелей қарау жолымен бекітілуі қажет. Триангуляция пункттерінің рекогносцировкасы кезінде қоныстанған аймақтарда ағаштарды қолданады немесе оларға елді мекенді көру үшін көтеріліп арнайы діңгектерді жасайды. Жүйенің класына қарамастан әр пунктте бағыттың магнитті азимуттарын, елді мекеннің нүктелеріне дейінгі қашықтықтарды және еркін масштабта басқа анықтамалар енгізілетін көкжиектің суретін салу жүргізіледі.
- пирамида - 3-5м;
- жай сигнал - 8-11м;
- күрделі сигнал - 11-30м.
2. 7 Пункттердің центрлері
Триангуляцияның немесе талдау жүйесінің әр пунктінде орталық салынады, оның түрі сол аймақтың физика-географиялық жағдайына байланысты орталықтардың қозғалмауын және ұзақ уақыт бойы сақталуын қамтамасыз ететіндей таңдалады.
Центрлердің құрылысын анықтайтын басты фактор топырақтың құрамы және қату тереңдігі болып табылады.
Центрлерді бетон блоктарынан немесе металл құбырлардан жасайды. Жартысфералы тесігі болатын басы бар барлық бұрыштық және сызықтық өлшемдерді келтіретін шойын маркаларды бетонға салады немесе құбырларға дәнекерлейді.
Құбырларды коррозиядан сақтау үшін цемент қоспасымен толтырады. Қазіргі уақытта орталықтардың 8 әр түрлерін қолданады.
Қалыпты жағдайларда топырақтың мезгілдік қатуы 1, 5м аспаған кезде және топырақтың қасиеттері котлован қазуға кедергі болмайтын жағдайда барлық класты пункттерде центрлердің түрі салынады.
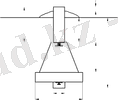
1. 5 -сурет. Пункттің центрі
Ол 4 бетон монолитінен тұратын пилон түрінде болады.
Монолит IV - 25-20см қабырғалы текше пішінді, жоғары жағына маркасы салынған.
Монолит III 60х60х20 өлшемді.
Монолит II биіктігі 130см, пішіні қималы төртжақты, маркасы жоғары жағында.
Монолит I биіктігі 70см, айыру бағанасы болып қызмет етеді.
Барлық монолиттер өзара цемент қоспасымен бекітілген.
2. 8 Базистер және базистік жүйелер
Инварлы сымы бар базисті құралды триангуляцияда базистік қабырғаларды өлшеу үшін, полигонометрияда қабырғалардың ұзындықтарын өлшеу үшін және инженерлік - геодезиялық жұмыстарды жасағанда басқа жоғары дәлдікті сызықтық өлшемдер үшін қолданылады.
Сызықтық өлшемдердің аса жоғары дәлдігі базисті құралды қолданумен қол жеткізілуі мүмкін 1:1 қатарлы салыстырмалы қателікпен сипатталады.
Инвар -30 0 Сден +100 0 С дейінгі температуралар интервалында тұрақты сызықтық кеңеюдің кіші температуралық еселігіне ие. Ол тотықтанбайды және өңдеуге жақсы бейімделген.
Мақсатына байланысты базисті құралдардың 3 түрін бөледі:
- БҚ-1 6 - 8 сымы бар, триангуляцияда және 1 және 2 класс полигонометриясында базистерді өлшеуге арналған;
- БҚ-2 және 4 сымы бар, базисті қабырғаларды және 3 мен 4 класс полигонометриясының қабырғаларын өлшеуге арналған;
- БҚ-3 және 2 немесе 4 сымы бар, жергілікті маңызы бар жүйелерде қабырғаларды және әр түрлі инженерлік-геодезиялық жұмыстар кезінде өлшеу үшін арналған.
Өлшеулер алдында құралдың дайындығын тексеру керек.
1. тұтастыру жүргізу және келесі түзетулерді енгізу:
-сымның ұштарын артық алған үшін:
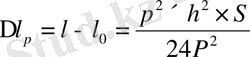 ; (3. 1)
; (3. 1)
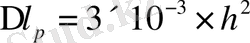 ; (3. 2)
; (3. 2)
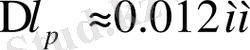 , (3. 3)
, (3. 3)
мұндағы S - сымның ұзындығы = 24м;
p - бір текше метр сымның салмағы = 0, 0173кг/м;
P - сымды тарту кезінде қолданылатын жүктердің салмағы = 10кг;
h = 2м.
-тізбекті желінің симметриясыздығы үшін түзету мардымсыз шамаға ие, бірақ ол әрқашан оң болғандықтан, ол өлшеудің дәлдігіне жүйелі әсер етеді;
- температураның өзгеруіне, яғни температураның 1 0 С өзгеруі кезінде сымның салыстырмалы ұзаруы 1:2 тез болады. Қателік жүйелі сипатқа ие емес;
- сымдардың тартылуының өзгеруі:
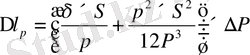
(3. 4)
мұндағы д - 1м сымның өзінің салмағының р әсерінен созылуы;
∆Р - созылудың өзгерісі, в кг;
р - жүктің салмағы;
S - сымның ұзындығы.
- сыртқы жағдайлары үшін түзету. Жел мен жаңбыр аса қатты әсер етеді. Желдің жылдамдығы ≈5м/сек болғанда өлшенетін қабырғаның салыстырмалы қателігі 1:5 құрайды. Есептеулер көрсеткендей, егер сымның беті қалыңдығы 0, 05мм ылғалмен басылып қалса, онда бұл қатардың салыстырмалы қысқаруын тудырады 1:5.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz