Кванттық механика элементтері

Пән: Физика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 4 бет
Таңдаулыға:

Кванттық механика элементтері

Заттардың толқындық қасиеттері. Луи де Броиль формуласы. Бұрын айтылғандай жарықтың екі жақты толқындық ( интерференция, дифракция, поляризация) және эффектісі (жарықтың қысымы ) қасиеті болатындығын білеміз француз физигі Де Броиль жарық фотондары сияқты, электрондардың да толқындық қасиеті болады деген болжам айтып, электрондардың толқын ұзындығын есептеуге арналған формула берген.

Фотонның энергиясы , екінші жағынан Эйнштейннің салыстырмалы теориясы бойынша масса мен энергияның арасында мынандай байланыс бар.

; ; ;

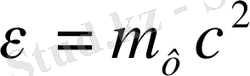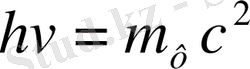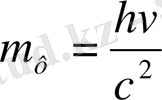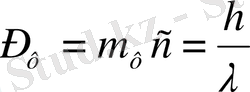
Сонда электронның импульсі

;

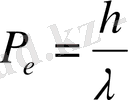
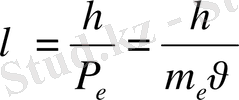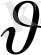-электронның жылдакмдығы. Егер электрон потенциалдар айырымы электр өрісінде үдемелі қозғалса ; ;

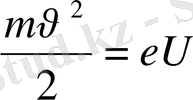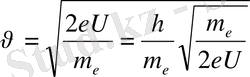Де Броиль толқын ұзындығы кристалдардың атомдық жазықтықтарының арақашықтығы мен шамалас болады. Олай болса, кристалдық ток Бройль толқындары үшін дифракциялық тор қызметін атқарады. Сондықтан электрондар шоғы кристалдан өткенде электрондардың дифракциясын бақылауға болады.

1927 ж Американ физиктері Дэвиссон мен Джермер электрондар шоғын никель кристалына түсіріп, одан шағылған электрондардың дифракция құбылысын байқаған. Осы тәжірибе Де Броиль болжамының дұрыстығын дәлелдеп, электрондардың толқындық қасиеті болатындығын көрсетті. Осындай электрондардың диффракциясын орыс ғалымдары Тартаковский, Фабрикант тәжірибе жүзінде бақылады. Жалпы алған толқындық қасиет тек электрондарға ғана тән емес, басқада кез келген (протон, нейтрон т. б. ) бөлшектерге де тән қасиет екендігін көреміз.

Гейзенбергтің анықталмаушылық принципі. Классикалық механикада қозғалатын кез-келген материалдық нүктенің (бөлшектің) белгілі бір траекториясы және кез келген уақытта оның координаты мен импульсін дәл анықтауға болады. Ал, көзге көрінбейтін ұсақ бөлшектер ( микробөлшектер) болса, өзінің толқындық егер де координат мәнін, дәл өлшесек, онда оны өлшеудегі кеткен қателік 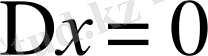болады, онда 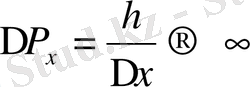болады, яғни бұл жағдайда импульстің мәнін өлшегенде кететін қателік болады. Ал, егер импульстің мәнін дәл өлшесек, онда координаттың белгілі бір мәні болмайды . Мысалы, атом ішінде қозғалатын электронды қарастырайық; яғни оның координатын анықтамақ болайық. Атомның радиусы 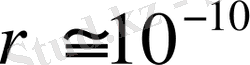м, сонда атом ішіндегі электронның координатын анықтаудағы кететін қате м болады. Сонда электронның жылдамдығын анықтаудағы кететін қате; 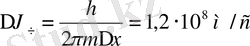болады.

Бұл электронның атомның ішіндегі жылдамдығына 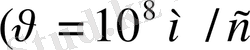тең екен. Сонда атом ішіндегі электронның жылдамдығын анықтаудағы қате сол жылдамдықтың өзіне тең болып отыр. Сондықтан атом ішінде электронның белгілі бір жылдамдықпен қозғалатын тұйықталған орбитасы бар деуіміз дұрыс емес.

Сонымен қатар кванттық теорияның негізінде уақыт пен энергияның анықтамаушылықтарды қарастырылады.

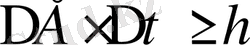
Осыдан белгілі бір жүйенің (бөлшектің) орташа өмір сүру уақыты дәл белгілі болса, онда ол жүйені сипаттайтын энергияны анықтауға болмайды. Керісінше -белгілі болса болады толқындық қасиеті болу есебінен классикалық бөлшектен ерекше айырмашылығы болады. Микробөлшектердің бір айырмасы, олардың траекториясы болмайды. Сондықтан бір мезгілде олардың координаттары мен импульстерін дәл анықтауға мүмкіншілік болмайды. Олай болса микробөлшектерді, макробөлшектерге тән шамалар мен тек жуықтап қана сипаттауға болады.

Осы пікірге байланысты толқындық механикада мынандай принцип бар: «Электронның (немесе кез-келген ұсақ бөлшектердің) орынын (координатын) және импульсін бір мезгілде дәл өлшеуге болмайды. Мысалы: фотонның х осі бойынша координатын өлшегендегі қателік болып, оның жылдамдығын өлшегендегі қателік болса, онда мына шарт орындалу керек: ;

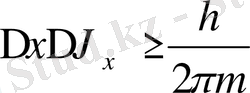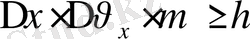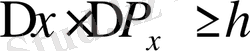; ; мұнда 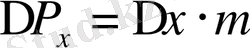-импульсті өлшеуге кеткендегі қателік.

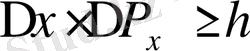
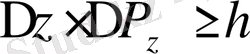
Осы теңсіздіктерді бірінші рет неміс физигі Гейзенберг ұсынған болатын. Сондықтан оны Гейзенбергтің анықталмаушылық теңсіздіктері деп атайды.

Зат бөлшектерін сипаттайтын әрі толқындық, әрі корпускалалық екі жақтылы универсалды теория деген де Бройль идеясын көптеген тәжірибелер растайды. Анықталмаушылық принцип классикалық физика заңдарын микробөлшектердің күйін сипаттау үшін қолдануға болмайтындығын көрсетті. Сондықтан микробөлшектердің қасиеттерін зерттеу үшін ХХ-ғасырдың бас кезінде жаңа теория, кванттық механика теориясы қалыптаса бастады. Бұл теория ұсақ бөлшектердің қозғалу заңдары мен өзара әсерлесуі олардың толқындық қасиеттеріне байланысты екендігін көрсетті.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.