«Сандық әдістер» пәнінен зертханалық жұмыстар. Оқу құралы

КІРІСПЕ 3
1 Жуықтап есептеу ережелері және есептеу қателіктерін бағалау
№1 зертханалық жұмыс. Қателіктер теориясы 4
2 Сызықты емес теңдеулер және теңдеулер жүйесі
№1 зертханалық жұмыс. Сызықты емес теңдеулерді шешудің сандық әдістері 8
№2.зертханалық жұмыс. Сызықты емес теңдеулер жүйесін шешудің сандық әдістері 16
3 Сызықты алгебралық теңдеулер жүйесін шешудің сандық
әдістері
№1 . зертханалық жұмыс. Cызықты алгебралық теңдеулер жүйесін сандық шешудің тура әдістері 21
№2 . зертханалық жұмыс. Сызықты алгебралық теңдеулер жүйесін сандық шешудің итерациялық әдістері 37
4 Интерполяциялау есебі
№1 . зертханалық жұмыс. Функцияны интерполяциялау 46
№2 . зертханалық жұмыс. Тәжірибелік деректерді өңдеу әдістері 59
5 Интегралдарды жуықтап есептеу
№1 зертханалық жұмыс. Сандық интегралдау есебі 69
6 Қарапайым дифференциалдық теңдеулерді жуықтап шешу
№1 . зертханалық жұмыс. Қарапайым дифференциалдық теңдеулерді шешудің бірқадамды Сандық әдістері 81
№2 . зертханалық жұмыс. Қарапайым дифференциалдық теңдеулерді шешудің көпқадамды сандық әдістері 90
7 Қарапайым дифференциалдық теңдеулер үшін шектік
есептерді жуықтап шешу
№1 зертханалық жұмыс. Қарапайым дифференциалдық теңдеулер үшін шектік есептер
№2.зертханалық жұмыс. Шектік есептерді шешудің вариациялық әдістері 96
8 Дербес туындылы дифференциалдық теңдеулерді жуықтап шешу
№1 зертханалық жұмыс. Дербес туындылы диффе.ренциалдық теңдеулерді шешудің сандық әдістері
№2 зертханалық жұмыс. Екі өлшемді Пуассон теңдеуі үшін Дирихле есебінің Delphi7 ортасындағы жобасы 115
Әдебиеттер тізімі 157

Сандық әдістер пәнінің физика-математика, инженер-технолог мамандықтарының студенттері үшін орны ерекше. Себебі дәл ғылыми сала болғандықтан математиканы да, информатиканы да, физиканы қамтитын бұл пәннің ғылыми, техникалық, физикалық есептерді шешуге тигізер көмегі көп. Күрделі есептерді классикалық әдістермен шығару мүмкін болмаған жағдайда сандық әдістердің ЭЕМ-де алгоритмдерін талдау бұл пәннің маңызын арттыра түседі. Пәнді оқыту барысында студенттерді аналитикалық жолмен шешілмейтін жоғарғы математика есептерімен таныстыра отырып, оны шешу әдістері талқыланады.
Қазіргі заман талабына сай ғылыми есептерді шешуде ЭЕМ рөлінің артуына байланысты сандық әдістерді студенттердің меңгеруіне көмектеседі.
Күрделі математикалық-физикалық процестерді зерттеу үшін математикалық моделі құрылып, оларды шешудің сандық әдістерінің алгоритмдері қарастырылады.
Сандық әдістердің түрлерін келтіре отырып, олардың біреуін таңдау барысында машинаның спецификасы ескеріледі. Сондай-ақ сандық әдістерді қолдану барысында пайда болатын қателіктерді анықтау әдістері келтіріледі. Қателіктердің түрлері, олардың есептің шешіміне тигізетін әсері қарастырылады. Оқу-әдістемелік құралда сандық әдістердің негізгі мазмұны келтірілген.
Бір есепті бірнеше әдіспен шығару алгоритмдері бар. Оларға программа құру арқылы алынған нәтижені бір-бірімен салыстыру барысында олардың айырмашылығын, тиімдісін анықтауға болады. Оқу құралына 10 зертханалық жұмыс енгізіліп отыр. Әр оқырман тақырыпқа байланысты қысқаша теориялық мағлұматтарды оқып, келтірілген мысалдарды саралап, берілген тапсырмаларды компьютер көмегімен және қарапайым есептеулер жүргізу арқылы орындап, алынған нәтижелерді салыстыруына болады. Кейбір зертханалық жұмысқа қатысты құрылатын программа нұсқасы берілген, бұл программалар студенттердің сандық әдістердегі формулаларды компьютер көмегімен өңдеулеріне көмекке жарайды деген мақсатпен келтіріліп отыр. Ал кейбір тақырыптарға программалар келтірілмеген, ол тақырыпқа қатысты программаны құру студенттерге берілетін өз бетімен жұмыс іспетті.

1. Ильин В.П. Разностные методы решения эллиптических уравнений.- Новосибирск, 1970.
2. Самарский А.А. Введение в теорию разностных схем. - Москва, 1971.
3. Марчук Г. И. Методы вычислительной математики - Новосибирск, 1973.
4. Рябеньский В.С., Филиппов А.Ф. Об устойчивости разностных уравнений.- Москва, 1956.
5. Годунов С.К., Рябеньский В.С. Разностные схемы. - Москва, 1973.
6. Тихонов А.Н., Самарский А.А. Уравнения математической физики. - Москва, 1966.
7. Лыков А.В.. Теория теплопроводности. - Москва, 1967.
8. Саульев В.К. Интегрирование уравнений параболического типа методом сеток. - Москва, 1960.
9. Годунов С.К., Рябеньский В.С. Введение в теорию разностных схем.- Москва, 1962.
10. Березин И.С., Жидков Н.П. Методы вычислений. т.1. Наука, 1966.
11. Воеводин В.В. Численные методы алгебры. Теория и алгорифмы. Наука, 1966.
12. Гавурин М.К. Лекции по методам вычислений. Наука, 1971.
13. Крылов А.Н. Лекции о приближенных вычислениях. - Гостехиздат, Москва-Л., 1950.
14. Коллатц Л.. Численные методы решения дифференциальных уравнений. ИЛ, 1953.
15. Ланцош К. Практические методы прикладного анализа. Физматгиз. 1961.
16. Милн В.Э. Численный анализ. ИЛ. 1951.
17. Милн В.Э. Численные методы решения дифференциальных уравнений. ИЛ. 1955.
18. Бриллюэн Л. Наука и теория информации.Физматгиз. 1961.
19. Лаврентьев М.М. О некоторых некорректных задачах математической физики. Изд-во СО АН СССР, Новосибирск, 1962.
20. Рябеньский В.С., А.Ф. Филиппов. Об устойчивости разностных уравнений. Гостехиздат. 1956.
21. Бахвалов Н.С.. Численные методы. –М.: Наука, 1973.
22. Березин И.С., Жидков Н.П.. Методы вычислений. –М.: Наука, 1966.
23. Коллатц Л.. Численные методы решения дифференциальных уравнений. –М.: ИЛ, 1953.
24. Коллатц Л., Альбрехт Ю., Задачи по прикладной математике. –М.: Мир, 1978.
25. Крылов В.И., Бобков В.В., Монастырный П.И.. Выичслительнгые методы высшей математики. –Минск, 1972.
26. Мысовский И.П.. Лекции по методам вычислений. –М.: Физматгиз, 1962.
27. Копченова Н.В., Марон И.А.. Вычислительная математика в примерах и задачах. –М.: Наука, 1972.
28. Демидович Б.П., Марон И.А.. Основы вычислительной математики. –М.: Наука, 1980.
29. Самарский А.А., Николаев Е.С.. Методы решения сеточных уравнений. –М.: Наука, 1978.
30. Вазов В., Дж.Форсайт. Разностные методы решения дифференциальных уравнений в частных производных. М., 1963.
31. Шпак Ю.В. Программирование в среде Дельфи. М.: Мир, 2000-350стр.
32. Культин В.В. Delphi7 в задачах и примерах. Санкт-Петербург.: Питер, 2001, - 465стр.
33. Кабланбекова Б.А. Дельфи программалау тіліне кіріспе. Әдістемелік құрал. Семей: Тенгри, 2006.

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 148 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТІРЛІГІ
С. АМАНЖОЛОВ АТЫНДАҒЫ ШЫҒЫС ҚАЗАҚСТАН МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ

Б.А. Кабланбекова

САНДЫҚ ӘДІСТЕР
пәнінен зертханалық жұмыстар

Оқу құралы

Өскемен
С. Аманжолов атындағы ШҚМУ баспасы
2011

ОӘЖ 519.6 (075.8)
ҚБЖ 22.11 я73
К 12

С.Аманжолов атындағы ШҚМУ әдістемелік кеңесімен
баспаға ұсынылған
№5 хаттама 21 маусым 2009 ж.

Пікір жазғандар:
Хисамиев Н.Г., физика-математика ғылымдарының докторы, профессор,
Тұрғанбаев Е.М., физика-математика ғылымдарының кандидаты,доцент,
Мухамедиева С.М., С.Аманжолов атындағы ШҚМУ, Математикалық үлгілеу және
компьютерлік технологиялар кафедрасының доценті

К 12 Кабланбекова Б.А. Сандық әдістер пәнінен зертханалық жұмыстар: Оқу
құралы. - Өскемен: С.Аманжолов атындағы ШҚМУ баспасы, 2011. - 160 б.

ISBN 978-601-80142-0-8

Сандық әдістер пәнінің зертханалық жұмыстарын жүргізуге арналған
оқу құралында заманауи есептеу әдістерінің көкейтесті сұрақтары
қарастырылды.

Қателіктер теориясы, сызықты емес теңдеулер және жүйелер, қарапайым
дифференциалдық теңдеулер, қарапайым дифференциалдық теңдеулер үшін
шекаралық есептер, сандық интегралдау, интерполяция есебі, айырымдық
теңдеулер, дербес туындылы дифференциалдық теңдеулер тақырыптары бойынша
теориялық материалдар негізінде аналитикалық әдістермен шешілуі қиын
математикалық, физикалық есептерді шешу алгоритмдері, компьютерлік
бағдарламалары келтірілді.

Оқу құралы жоғарғы оқу орындарының 5В011100-Информатика, 5В060200-
Информатика мамандықтарының студенттеріне, оқытушыларына, күрделі
математикалық, физикалық есептерді сандық шешу әдістері қызықтыратын
оқырмандарға арналады.

ISBN 978-601-80142-0-8

ОӘЖ 519.6 (075.8)
ҚБЖ 22.11 я73

ISBN 978-601-80142-0-8
© Кабланбекова Б.А., 2011
МАЗМҰНЫ
КІРІСПЕ 3
1 Жуықтап есептеу ережелері және есептеу қателіктерін бағалау 4
№1 зертханалық жұмыс. Қателіктер теориясы
2 Сызықты емес теңдеулер және теңдеулер жүйесі 8
№1 зертханалық жұмыс. Сызықты емес теңдеулерді шешудің сандық
әдістері
№2-зертханалық жұмыс. Сызықты емес теңдеулер жүйесін шешудің сандық16
әдістері
3 Сызықты алгебралық теңдеулер жүйесін шешудің сандық 21
әдістері
№1 – зертханалық жұмыс. Cызықты алгебралық теңдеулер жүйесін сандық
шешудің тура әдістері
№2 – зертханалық жұмыс. Сызықты алгебралық теңдеулер жүйесін сандық37
шешудің итерациялық әдістері
4 Интерполяциялау есебі 46
№1 – зертханалық жұмыс. Функцияны интерполяциялау
№2 – зертханалық жұмыс. Тәжірибелік деректерді өңдеу әдістері 59
5 Интегралдарды жуықтап есептеу 69
№1 зертханалық жұмыс. Сандық интегралдау есебі
6 Қарапайым дифференциалдық теңдеулерді жуықтап шешу 81
№1 – зертханалық жұмыс. Қарапайым дифференциалдық теңдеулерді
шешудің бірқадамды Сандық әдістері
№2 – зертханалық жұмыс. Қарапайым дифференциалдық теңдеулерді 90
шешудің көпқадамды сандық әдістері
7 Қарапайым дифференциалдық теңдеулер үшін шектік 96
есептерді жуықтап шешу
№1 зертханалық жұмыс. Қарапайым дифференциалдық теңдеулер үшін
шектік есептер
№2-зертханалық жұмыс. Шектік есептерді шешудің вариациялық әдістері106
8 Дербес туындылы дифференциалдық теңдеулерді жуықтап шешу 115
№1 зертханалық жұмыс. Дербес туындылы диффе-ренциалдық теңдеулерді
шешудің сандық әдістері
№2 зертханалық жұмыс. Екі өлшемді Пуассон теңдеуі үшін Дирихле
есебінің Delphi7 ортасындағы жобасы 149
Әдебиеттер тізімі 157

КІРІСПЕ

Сандық әдістер пәнінің физика-математика, инженер-технолог
мамандықтарының студенттері үшін орны ерекше. Себебі дәл ғылыми сала
болғандықтан математиканы да, информатиканы да, физиканы қамтитын бұл
пәннің ғылыми, техникалық, физикалық есептерді шешуге тигізер көмегі көп.
Күрделі есептерді классикалық әдістермен шығару мүмкін болмаған жағдайда
сандық әдістердің ЭЕМ-де алгоритмдерін талдау бұл пәннің маңызын арттыра
түседі. Пәнді оқыту барысында студенттерді аналитикалық жолмен шешілмейтін
жоғарғы математика есептерімен таныстыра отырып, оны шешу әдістері
талқыланады.
Қазіргі заман талабына сай ғылыми есептерді шешуде ЭЕМ рөлінің артуына
байланысты сандық әдістерді студенттердің меңгеруіне көмектеседі.
Күрделі математикалық-физикалық процестерді зерттеу үшін
математикалық моделі құрылып, оларды шешудің сандық әдістерінің
алгоритмдері қарастырылады.
Сандық әдістердің түрлерін келтіре отырып, олардың біреуін таңдау
барысында машинаның спецификасы ескеріледі. Сондай-ақ сандық әдістерді
қолдану барысында пайда болатын қателіктерді анықтау әдістері келтіріледі.
Қателіктердің түрлері, олардың есептің шешіміне тигізетін әсері
қарастырылады. Оқу-әдістемелік құралда сандық әдістердің негізгі мазмұны
келтірілген.
Бір есепті бірнеше әдіспен шығару алгоритмдері бар. Оларға программа
құру арқылы алынған нәтижені бір-бірімен салыстыру барысында олардың
айырмашылығын, тиімдісін анықтауға болады. Оқу құралына 10 зертханалық
жұмыс енгізіліп отыр. Әр оқырман тақырыпқа байланысты қысқаша теориялық
мағлұматтарды оқып, келтірілген мысалдарды саралап, берілген тапсырмаларды
компьютер көмегімен және қарапайым есептеулер жүргізу арқылы орындап,
алынған нәтижелерді салыстыруына болады. Кейбір зертханалық жұмысқа
қатысты құрылатын программа нұсқасы берілген, бұл программалар
студенттердің сандық әдістердегі формулаларды компьютер көмегімен
өңдеулеріне көмекке жарайды деген мақсатпен келтіріліп отыр. Ал кейбір
тақырыптарға программалар келтірілмеген, ол тақырыпқа қатысты программаны
құру студенттерге берілетін өз бетімен жұмыс іспетті.
1 ЖУЫҚТАП ЕСЕПТЕУ ЕРЕЖЕЛЕРІ ЖӘНЕ ЕСЕПТЕУ
ҚАТЕЛІКТЕРІН БАҒАЛАУ

№1-зертханалық жұмыс
Қателіктер теориясы

Шамалардың жуық мәндері жуық сандармен беріледі.
Сандық әдістер немесе есептеу әдістері пәндерінде алынған
нәтижелердің барлығы жуық шешімдер деп аталады.
Тура шешім мен жуық шешім айырмасы әдіс қателігі немесе дөңгелектеу
қателігі деп аталады.
Қателіктер 3 түрге бөлінеді:
1. Әдіс қателігі
2. Шеттетілмейтін қателік
3. Есептеу қателігі
Әдіс қателігі берілген есепті шешу үшін таңдалған сандық әдістен
тәуелді болады. Осыған байланысты әр әдістің қателігін бағалау формуласы әр
түрлі болады.
Шеттетілмейтін қателіктер – есептің бастапқы берілгендерінен,
коэффициенттерінен, шарттарынан тәуелді қателіктер.
Есептеу қателігі жуық шешімдерді алу барысында қолданылатын
математикалық есептеулер кезінде қолданылатын сандарды дөңгелектеуден
тәуелді.

Қателіктер теориясындағы негізгі ұғымдар

Бұл қателіктердің өздері абсолютті және салыстырмалы ([3] қараңыз)
болады.
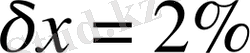
1. Егер а саны – тура мән, а* саны оған белгілі жуықтау болса, онда
жуықтаудың абсолютті қателігі деп - олардың айырымын, ал
шектік абсолютті қателігі деп мына шартты қанағаттандыратын
қателікті айтады: .
2. Жуықтаудың салыстырмалы қателігі деп келесі шартты
қанағаттандыратын шартты айтады: немесе .
3. Санның мәнді цифрлары деп оның жазылуындағы солдан бастағанда
нөлден өзгеше барлық цифрларын айтады.
4. Мәнді цифрды дұрыс дейді, егер санның абсолютті қателігі осы цифрге
сәйкес разряд бірлігінің жартысынан аспаса.

Арифметикалық операциялар нәтижелерінің қателіктері

1. Қосынды қателігі. F(x)=x=x1+x2+x3+...+xn қосындысы берілсін.
a) қосындының абсолютті қателігі: .
Егер болса, онда , ал n=10 болса, Чеботарев формуласы
қолданылады: .
b) қосындының салыстырмалы қателігі:
. Мұндағы , , .
2 Айырма қателіктері. X=x1-x2, x1x20 болсын және азайғыш пен
азайтқыштың жуық мәндері мен абсолютті қателіктері белгілі болсын.
a) айырманың абсолютті қателігі: .
b) айырманың салыстырмалы қателігі:
.
3 Көбейтіндінің қателіктері. X=x1*x2*...*xn көбейтіндісі берілсін.
Көбейткіштердің жуық мәндері және абсолютті, салыстырмалы
қателіктері белгілі болсын.
a) көбейтіндінің абсолютті қателігі:
.
b) көбетіндінің салыстырмалы қателігі: .
4 Бөліндінің қателігі: бөліндісі берілсін. Алымы мен
бөлімінің жуық мәндері, абсолютті, салыстырмалы қателіктері
берілген болсын.
a) бөліндінің абсолютті қателігі: .
b) бөліндінің салыстырмалы қателігі: .
1- мысал: Берілген х санының дұрыс цифрлар санын анықтау керек болсын.
; .
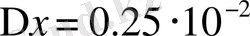Анықтама бойынша: 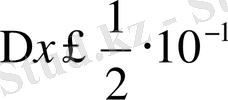шарты орындалса, 3 цифрын дұрыс цифр деуге болады.
Шындығында 0,00250,05 екен, яғни 3 - дұрыс цифр. 9 цифрын тексерсек:
0,00250,005, яғни 9 цифры да дұрыс. Ал 4 пен 1 цифрлары үшін 0,00250,0005
және 0,00250,00005 болғандықтан, олар күмәнді цифрлар болады. Қорыта
айтқанда үтірден кейінгі 3 және 9 цифрларын жоғалтпау керек, яғни санды
0,39 деп дөңгелектеуге болады, 0,4 деп дөңгелектесек дөңгелектеу қателігі
өсіп кетеді. Санның дұрыс цифрлар саны төртеу.
2-мысал: 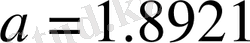; 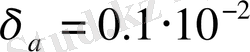берілген. Санның дұрыс цифрларын анықтау.
Анықтама бойынша: 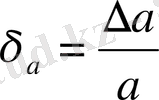, яғни 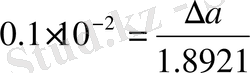. Одан шығатыны: 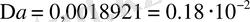. Енді санның
цифрларын тексереміз:
8 цифры - дұрыс, өйткені: .
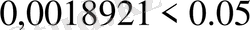9 цифры – күмәнді, өйткені: 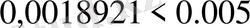. Дәл осылай 2 және 1 цифрларының да
күмәнді екенін анықтауға болады. Сонда а санының 2 цифры дұрыс.
3-мысал: Х=2,1514 санын 3 мәнді цифрға дейін дөңгелектеп, абсолютті және
салыстырмалы қателіктерін табу.
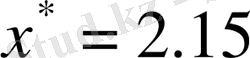болады. Сонда , .
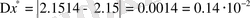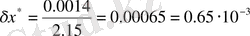4-мысал: 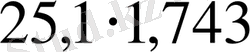көбейтіндісінің абсолютті және салыстырмалы қателіктерін
анықтау.
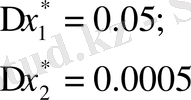екені белгілі. .
.

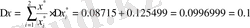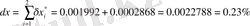Тапсырмалар

1. Келесі сандарды 3 мәнді цифрға дейн дөңгелектеп, алынған жуық
мәндердің абсолютті және салыстырмалы қателіктерін анықтаңыздар:

a) 2,1514
b) 0,16152
c) 0,01204
d) 1,225
e) -0,0015281
f) -392,85

2. Салыстырмалы қателіктері белгілі келесі сандардың абсолютті
қателіктерін анықтаңыздар:

a) a=13267,
b) a=2.32,
c) a=35.72
d) a=0.896
e) a=232.44

3. Абсолютті қателіктері белгілі жуық сандардың дұрыс таңбаларының санын
анықтаңыздар:
a) X=0.3941
b) X=0.1132
c) X=38.2543
d) X=293.481
e) X=2.325
f) X=14.00231
g) X=-32.285

4. Салыстырмалы қателіктері белгілі жуық сандардың дұрыс таңбаларының
санын анықтаңыздар:

a=1.8921
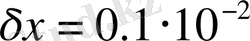
a=0.2218
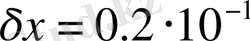
a=22.351
a=0.02425
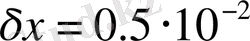
a=9.3598
a=0.11452
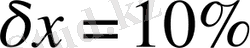
a=592.8

2 СЫЗЫҚТЫ ЕМЕС ТЕҢДЕУЛЕР ЖӘНЕ ТЕҢДЕУЛЕР ЖҮЙЕСІ

№1 зертханалық жұмыс

Сызықты емес теңдеулерді шешудің сандық әдістері

Сандық әдістердің бір бөлімі бір өлшемді сызықты емес теңдеулер
болып табылады. Физикалық және басқа да құбылыстардың теңдеумен
сипатталатыны белгілі. Сол теңдеуді классикалық математикалық формуламен
шешу мүмкін емес жағдайлар бар. Бұл уақытта практикада сандық әдістерге
жататын әдістермен шешілетінін дәлелдеу керек. Әрине ең алдымен құрылған
теңдеудің қай аралықта анықталғандығын, үзіліссіздігін, түбірінің барлығын,
оның жалғыздығын дәлелдейтін аргументтерді бақылау керек. Осы этаптан
өткеннен кейін ғана есепті осы теңдеуге қолдануға келетін алгоритм
көмегімен шығаруға болады.
Сызықты емес теңдеулер екі түрлі:
1. Алгебралық;
2. Трансцендентті;
Алгебралық теңдеулер деп алгебралық көпмүшеліктерден тұратын
теңдеулерді айтады. Олардың шешімдері көбіне нақты сан болады.
Трансцендентті теңдеу деп құрамында тригонометриялық немесе арнаулы
функцялары бар теңдеуді айтады.
Сызықты емес теңдеуді сандық шешу екі тәсілден ([1] қараңыз) тұрады.
1 Тура тәсіл - есепті математикалық дәлелденген бір формулаға қою
арқылы тікелей шығару;
2 Итерациялық тәсіл – есепті формула көмегімен бастапқы жуықтауды
беру арқылы жуықтап, біртіндеп шығару;
Тура тәсілмен шығарылған есептер дәл мәнді береді. Ал итерациялық
тәсілмен шешілген есептер есептің жуық мәнін береді .Мұның ішінде
итерациялық әдістер сандық әдіске жатады.
Бір өлшемді сызықты емес теңдеуді шешудің келесі әдістері бар.
1 Кесіндіні қақ бөлу - дихотомия әдісі деп аталады;
2 Хорда әдісі;
3 Жанама әдісі немесе Ньютон әдісі;
4 Қарапайым итерациялық әдіс немесе жәй итерация әдісі т.б.;
Түбір жатқан аралықты анықтау әдісі
F(x)=0 (2.1)
Бірөлшемді сызықты емес теңдеу берілген. Мұндағы F(x) функциясы [a,b]
кесіндісінде анықталған және үзіліссіз болсын.

Теорема1.1: [а,в] аралығында анықталған, үзіліссіз F(x) функциясының
екі шеткі нүктелердегі мәндерінің таңбалары әр түрлі болса, яғни мына
шарт орындалса f(a)*f(b)0, онда осы аралықта (2.1)-теңдеудің түбірі
бар және жалғыз болады.

Практикада кейде теореманың орындалуын функцияның мәндер кестесін құру
арқылы да анықтайды. Функцияның анықталу облысы бойынша а нүктесін беріп,
ол нүктедегі функция мәнін анықтайды, сосын һ қадаммен келесі нүктеге
жылжып, сол нүктедегі функция мәнін анықтайды, сол сияқты бірнеше нүктедегі
функция мәндерін анықтап, таңбасын салыстырады. Егер көрші нүктелерде
функция әр түрлі таңба қабылдаса, сол аралықта жалғыз түбірі жатыр деп
айтады.
1-мысал:
Берілген теңдеудің түбірін анықтау:

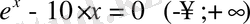
Теңдеудің түбірі жатқан аралықты аналитикалық тәсілмен табамыз: ол
үшін функция туындысын тауып, оны нөлге теңестіру арқылы экстремумдарын
анықтаймыз: 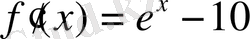, экстремумы: х1=Ln10=2,3;
Экстремум нүктелеріндегі функция таңбасының 1-кестесін толтырамыз.

1-кесте- 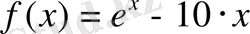функциясының таңбасын анықтау
Нүктелер 2,3
sign(f) + - +

Функция таңбасының ауысуы (; 2,3] және [2,3; ) аралығында
байқалды. Яғни осы аралықта теңдеудің түбірі бар.
Енді графиктік әдісті қарастырайық. Ол үшін теңдеуді мына түрлерге
жіктейміз, себебі функция күрделі, трансцендентті, бірден графигін құруға
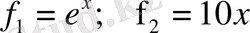болмайды: . Екі функцияның графигін саламыз, екеуінің қиылысқан
нүктесі теңдеудің түбірі болып табылады (1-сурет). Қиылысу нүктелерінің
аймақтарын анықтаймыз.

1-сурет- 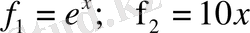функцияларының графиктері

Бірінші түбірі [0,1] аралығында, ал екінші түбірі [2,6] аралығында
жататыны суретте көрініп тұр. Енді осы аралықтағы қай нүкте (2.1)-ші
теңдеуді қанағаттандыратынын анықтаймыз.

Программасы
program Otdel_koren;
label 1,2,3;
var a,b,h,x1,x2,y1,y2:real;k:integer;
function f(x:real):real;
begin
f:=exp(x)-10*x;
end;
begin
writeln('аралыкты және кадамды енгізу');
read(a,b,h);
k:=0;
x1:=a;
x2:=x1+h;
y1:=f(x1);
2: if x2b then goto 1
else
begin
y2:=f(x2);
if y1*y20 then goto 3
else
begin
k:=k+1;
writeln(k,'-ші түбір=','[',x1:3:3,' ',x2:3:3,']');
end;
3: x1:=x2;x2:=x1+h; y1:=y2;
goto 2;
end;
1: end.

Кесіндіні қақ бөлу әдісі

(2.1) - теңдеуді кесіндіні қақ бөлу әдісімен шешу алгаритмі келесі
қадамнан тұрады.
1. (2.1)-ші теңдеудің түбірі жатқан аралығын анықтау және осы аралықта
түбірдің жалғыздығын тексеру. Яғни x осі бойында бірдей қашықтықта
жатқан нүктелердегі функцияның мәндерін есептеміз, және егер екі
шеткі нүктеде немесе екі көрші нүктеде функция мәндерінің таңбалары
әр түрлі болса, онда сол аралықта түбір бар деп есептеу
2. Осы аралықты қаққа бөлу және ол нүктенің мәнін
Xорт=(Xn+1+Xn)\2 (2.2)
формуласымен анықтау.
3. Xn+1-Xne шарты арқылы қарастырылып отырған аралықтан шығып
кетпеуді бақылаймыз.
4. XОРТ нүктесіндегі функция мәнін F(XОРТ) есептеу.
5. Егер оның таңбасы F(Xn) функциясының таңбасымен бірдей болса, Xn
нүктесінің орнына XОРТ нүктесін қарастырамыз.
6. Ал егер F(XОРТ) функциясының таңбасы F(Xn+1) функциясының
таңбасымен бірдей болса, Xn+1 нүктесінің орнына ХОРТ нүктесін
қарастырамыз.
7. Шыққан аралықтар [Xn,, Хорт] U [Xорт, Xn+1] белгіленеді.және
алдыңғы шарттарға байланысты екі аралықтың біреуін тағы қаққа бөлу
арқылы ізделінді нүктеге біртіндеп жақындаймыз. Яғни мына шарттар
тексеріледі: F(Xn+1)*F(Xорт)0 шарты орындалса [Xорт,Xn+1] аралығы
қаққа бөлінеді де шыққан нүкте мәні, XОРТ2=XОРТ+Xn+12 формуласымен
есептеледі. F(Xn)*F(ХОРТ)0 шарты орындалса [Xn,Xорт] аралығы қаққа
бөлініп, табылған нүкте XОРТ2=XОРТ+ Xn2 формуласымен есептеледі.
8. Осы процесті іздеп отырған х нүктесіне жеткенге дейін жалғастырып,
XОРТ, XОРТ2, XОРТ3, ..., XОРТN тізбегін құрамыз. Мына шарт
орындалатын уақытта XОРТN - XОРТN-1E іздеу процесін тоқтатамыз
да XОРТN нүктесін (2.1)-ші теңдеуді қанағаттандыратын х дәл түбірге
жуық мән деп қабылдаймыз.

Программасы
Program bisekzia;
Label 1;
Var a,b,e,c:real;
Function f(x:real):real;
Begin
F:=exp(x)-10*x;
End;
Begin
Writeln(‘аралықты және епсилонды енгізіңіз’);
Read(a,b,e);
1: c:=(a+b)2;
if abs(b-a)e then
write(‘x=’,c)
else
begin
if f(c )*f(a)0 then b:=c else a:=c;
goto 1;
end;
writeln(exp(c )-10*c);
end.
Жай итерация әдісі

Бұл әдісті қолдану үшін (2.1)-ші теңдеудің сызықты мүшесі айшықталып
мына түрге келтіру керек:

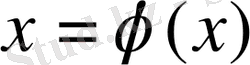(2.3)
Сосын теңдеудің түбіріне кез келген Х0 бастапқы жуықтау беріп
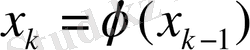k=1,2,... формуласымен х1, х2,...,хn нүктелер тізбегін құрамыз. Бұл тізбек x=z
түбіріне жинақталуы керек. Егер limXk=z болса, онда z нүктесі
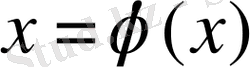теңдеуінің түбірі бола алады. Итерация әдісінің жинақтылық шарты 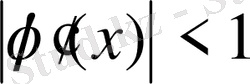және
бастапқы жуықтау кез келген болады. Итерациялық процесс берілген дәлдікке
жетуі үшін 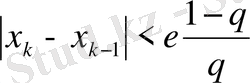шарты орындалуы керек.
Итерациялық тізбектің жинақтылығы теореманың ([1] қараңыз) шарттарымен
де тексерілуі керек:

Теорема1.2.:
теңдеуінің [a,b] аралығында жалғыз түбірі бар және келесі шарттар
орындалсын:
1функциясы [a,b] аралығында анықталған және дифференциалданады;
2 үшін ;
3 барлық үшін болатындай q саны табылсын,
онда , (k=1,2,...) итерациялық тізбегі кез келген бастапқы
жуықтауда жинақталады.

Теңдеуді итерациялық түрге келтіру

(2.1)-теңдеуді (2.3)-ші итерациялық түрге келтіру әртүрлі тәсілдермен
орындалады. Қай тәсілмен итерациялық түрге келтірілсе де жоғарыдағы
теореманың шарттары орындалуы керек. Практикада көрінгендей, теореманың 3)-
ші шартының орындалуы күрделірек, сондықтан төмендегі тәсілдердің бірін
қолдануға болады:
1 (2.1)-теңдеуді 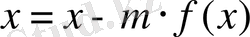түріне келтірейік, мұндағы m=const нөлден өзгеше. Бұл
уақытта 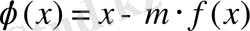деуге болады. Оны дифференциалдасақ: 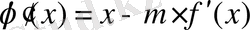. Теореманың 3)-ші
шарты орындалуы үшін үшін 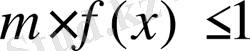шарты орындалатындай етіп m-ді таңдап
алу керек.
2 (2.1)-теңдеу (2.3)-ші түрге келтірілген, бірақ теореманың 3)-ші шарты
орындалмай тұрса, онда y= 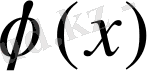функциясының орнына x=g(y) функциясын
қарастыруға болады. Мұндағы g(y) функциясы 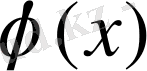функциясының кері
функциясы. Енді y=g(y) теңдеуін шешетін боламыз. Немес ескі белгілеулер
бойынша x=g(x) теңдеуін шешеміз деген сөз. Кері функциялардың
туындыларының қасиеттері бойынша .

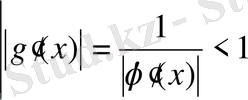2 – мысал

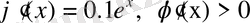
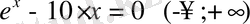теңдеуінің түбірін қарапайым итерация әдісімен табу керек болсын.
Теңдеуді итерациялық түрге келтіреміз:
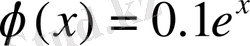. Ал және барлық х
нүктелері үшін
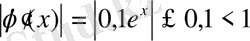. Яғни q=0,1 деп алып, бастапқы жуықтауды х0=0 десек 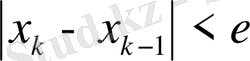шарты
орындалғанша итерациялық процесті құрамыз: х0=0: 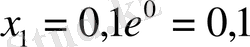; 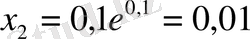, т.с.с. Түбір
мәні х6=0,111833, итерация саны 5-ке тең.

Хорда әдісі

Бұл әдіс кесіндіні қаққа бөлу әдісіне қарағанда шешімге тез
жинақталады.

Алгоритмі:
1. хn , xn+1 аралығында f (x) және f (xn+1) функцияларының таңбасы
бір біріне қарама-қарсы және түбірі бар болсын.
2. Осы екі шеткі нүктеден хорда жүргізіп, хорданың х осімен
қиылысқан нүктесін мына формуламен анықтаймыз.
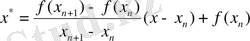(2.4)
Егер f(a)0 шарты орындалса, а нүктесі тұрақты болады да
формуласымен есептеледі
Егер f(b)0 шарты орындалса, b нүктесі тұрақты болады да
формуласымен есептеледі
3. х* нүктесіндегі функция мәнін F(x*)-ны есептеу. Оның таңбасын екі
шеткі нүктедегі функцияның таңбасымен салыстырылады. Егер f (xn)
және f(x*) функциясының таңбасы бірдей болса, онда хорданы xn+1
және x* нүктесі арқылы жүргізіледі. Оның мәнін (2.4) формуламен
табады. Егер f(xn+1) мен f(x*) функцияның таңбалары бірдей болса,
онда хорданы xn және x* нүктесі арқылы жүргізіледі. Шыққан
нүктенің мәні (2.4) формуламен есептелінеді.
4. x* нүктедегі мәнін есептеп, мәні нөлге жуық болса , онда x*
нүктесі (2.1) теңдеудің түбірі деп аталады. Егер нөлге жуық
болмаса, онда процесс жалғасады.
Алдындағы мысал үшін программасы келесідей болады:

Ньютон әдісі

Алдыңғы әдістерге қарағанда бастапқы жуықтау дұрыс таңдалынып алынса
Ньютон әдісі тез жинақталады. Бұл әдіске қатысты теореманы келтіре кетейік:
Теорема 1.3.: f(x) функциясы [a,b] аралығында анықталған және екі
ретті туындысы бар, осы аралықта түбір жатыр f(a)*f(b)0, туындылардың
таңбалары осы аралықта тұрақты болса f(x)*f'(x)0, онда
f(x0)*f''(x0)0 теңсіздігін қанағаттандыратын бастапқы
жуықтаудан бастап (2.1)-ші теңдеуді қанағаттандыратын [a,b]-да жататын
жалғыз шешімге жинақталатын итерациялық тізбек құруға болады.

Ньютон әдісінің геометриялық мағынасы: координаталары (xn;f(xn)) ,
болатын нүктеден қисыққа жанама жүргізсек, оның ох өсімен қиылысу нүктесі
теңдеудің түбіріне хn+1 – кезекті жуықтау болып табылады.
Түбірге n-ші жуықтаудың қателігін бағалау үшін келесі теңсіздіктің
орындалуын қадағалау керек: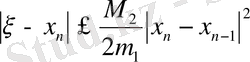. Мұндағы М2 – функцияның екінші ретті
туындысының аралықтағы максимумы, m1- минимумы. Егер, 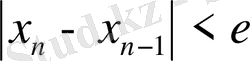болса, онда
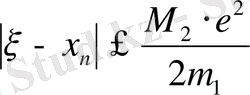болады, яғни түбірге дұрыс жуықталынса, әр итерациядан кейін кезекті
жуықтаудың ондық таңба саны екіге артады да процесс тез жинақталады. Егер
түбірді берілген е дәлдікпен табу керек болса, итерациялық процесті
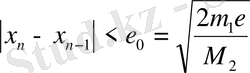шарты орындалғанша жалғастырамыз.
Бұл біртіндеп жуықтау әдісі деп аталады. Әдістің жинақталу жылдамдығы
х0 бастапқы нүктені дұрыс таңдауға байланысты. Егер итерация процесінде
функцияның туындысы нөлге тең болса, қисыққа жүргізілген жанама осіне
параллель болса, онда бұл әдісті қолдану қиындайды. Сол сияқты функцияның
екінші ретті туындысының мәні шексіз үлкен болса және функцияның өзі
бірінші ретті туындысы нөлге тең болса, онда шыққан түбірлер еселі болып,
жинақталмауы мүмкін. Бұл әдісті қолдану үшін функциясы үзіліссіз және
дифференциалданған болуы керек.
бастапқы жуықтауды таңдалынған уақытта құрылатын тізбек монотонды
кемімелі болуы керек.

Алгоритмі:
1. Қисықтың бойынан қандайда бір нүктесін таңдап, осы нүкте
арқылы қисыққа жанама жүргізіледі.
2. Жанама осін қиған кезде табылған нүктенің мәні мына формуламен
есептелінеді.
, (2.5)

Табылған нүктедегі функцияның мәні нөлге өте жуық болса, онда сол нүкте
(2.1) теңдеудің түбірі, болмаса процесс жалғасады.
Егер түбірлер еселі болса, ол еселікті деп белгілейік.
, (2.6)

Программасы

Program Nuwton;
Var x0,x1,e:real;
Label 1;
Function f(x:real):real;
Begin
F:=exp(x)-10*x;
End;
Function f1(x:real):real;
Begin
F1:=exp(x)*10;
End;
Begin
Read(x0,e);
1: x1:=x0-f(x0)f1(x0);
while abs(x1-x0)e do
begin
x0:=x1; goto 1;
end;
writeln(‘x=’,x:4:3);
end.

Тапсырмалар

Берілген теңдеулердің түбір жатқан аралығын тауып, жоғарыда
келтірілген сандық әдістермен түбірлерін анықтау. Әр түрлі әдіспен
анықталған түбірлерді бір бірімен салыстырып қателіктерін көрсету. Дәлдікті
өздеріңіз таңдап алыңыздар.

№ Теңдеулер түсіндірме
1 (0,2x)3=cos(x)
2 x-10sin(x)=0
3 2-x=sin(x) X10
4 2x-2cos(x)=0 x-10
5 Lg(x+5)=cos(x) X5
6
7 xsin(x)-1=0
8 8cos(x)-x=6
9 Sin(x)-0,2x=0
10 10cos(x)-0,1x2
11 2lg(x+7)-5sin(x)=0
12 4cos(x)+0,3x=0
13 5sin(2x)=
14 1.2x4+2x3-24.1=13x2+14.2x
15 2x2-5=2x
16 2-x=10-0,5x2
17 4x4-6.2=cos(0.6x)
18 3sin(8x)=0,7x-0,9
19 1.2-ln(x)=4cos(2x)
20 Ln(x+6.1)=2sin(x-1,4)

№2-зертханалық жұмыс
Сызықты емес теңдеулер жүйесін шешудің сандық әдістері

Екі теңдеуден тұратын екі белгісізді сызықты емес теңдеулер жүйесін
қарастырайық:
(2.7)
Бұл есептің мақсаты - екі теңдеудің графигінің қиылысу нүктелерін
анықтау.

Ньютон әдісі
Екі теңдеудің графигін сызып екеуінің қиылысу нүктелері жатқан облысты
белгілейміз де осы облыстан жуықтап бастапқы жуықтауларды (x0, y0) таңдап
аламыз ([3] қараңыз). Келесі жуықтауларды мына формулалармен есептейміз:

Мұндағы якобиан деп аталады.
Бұл әдіс бастапқы жуықтаулар түбірге жақын алынған уақытта тиімді.
Мысалы:

жүйесі берілген. Теңдеулердің графигін сызу (2-суретте.) арқылы бастапқы
жуықтауларды табамыз

2-сурет – және функцияларының графиктері

2-суреттен көріп отырғанымыздай, x0=1.2; y0=1.7 деп аламыз.
Якобианды есептейміз:
; n=0,1,2,..

Ньютон формуласына қойсақ:

осылайша біртіндеп (х2,у2), (х3,у3), ... жұптарының мәндерін F және G
функцияларының мәні нөлге жуықтағанша есептейміз.

Қарапайым итерация әдісі

(2.7)-ші жүйе берілсін. Бұл әдісті қолданбас бұрын жүйені итерациялық
түрге келтіріп алады:
(2.8)
Теңдеулердің графиктерін құру арқылы бастапқы жуықтауларды беріп, келесі
жуықтауларды мына формуламен есептейді:
n=0,1,2,... (2.9)
Бұл әдістің жинақтылығын теореманың шарттарымен тексеру керек.

Теорема 1.4: Әлдебір тұйық облыста (2.7)-ші
жүйенің жалғыз шешімдері бар болсын: . Егер:
1 және функциялары облысында анықталған және
үзіліссіз болса,
2 бастапқы және келесі жуықтаулардың барлығы осы облыста жатса,
3 осы облыста мына теңсіздіктер орындалса:
(2.10)
онда (2.8)-ші итерациялық процесс өзінің жалғыз шешіміне
жинақталады, яғни , .

Қателігін бағалау:
. M=max(q1;q2).

Кей жағдайда (2.8)-ші итерациялық процестің орнына Зейдель процесін
қолдануға болады:
n=0,1,2,... (2.11)

Жүйені итерациялық түрге келтіру

(2.7)-ші жүйені (2.8)-ші итерациялық түрге келтіру үшін келесі
тәсілдерді қолданған дұрыс.
, болсын. (2.12)
Коэффициенттерді мына жүйеден табамыз:

(2.13)
Параметрлерді осылай таңдап алу арқылы (2.10)-ші шарттың орындалуын талап
етуге болады.

1-мысал:

Берілген жүйе үшін итерациялық функцияларды таңдау.

х0=0.8, y0=0.55
Шешімді мына түрде іздейміз:
(2.14)
Коэффициенттерді анықтау үшін (2.13)-жүйе құруымыз керек, ол үшін дербес
туындылардағы мәндерді есептейміз:

(2.15)
.
(2.15)-ті (2.13)-ке қойсақ:
(2.16)
(2.16)-ны шешеміз:
, , , . Сонда .
Бұл мәндерді (2.14)-ші жүйеге қойсақ:

Есепті әрі қарай шешу үшін (2.9)-ші немесе (2.11)-ші итерациялық процесті
құру керек.

Тапсырмалар

Берілген сызықты емес теңдеулер жүйелерінің түбірлерін Ньютон,
Зейдель, қарапайым итерация әдістерімен анықтау.

№ Жүйелер Қосымша шарт
1
2 Y=0, y=x, x=0.5 түзулерімен шектелген
облыстағы түбірлерін табу.
3
Y=0, y=x, x=0.5 түзулерімен шектелген
облыстағы түбірлерін табу.
4 Y=0, y=x, x=0.5 түзулерімен шектелген
облыстағы түбірлерін табу.
5 Y=0, y=x, x=0.5 түзулерімен шектелген
облыстағы түбірлерін табу.
6 x0, y0, , k=0.1*m,
m=0,1,2,3,4.
7 x0, y0, , k=0.6+0.1*m,
m=0,1,2,3,4.

3 СЫЗЫҚТЫ АЛГЕБРАЛЫҚ ТЕҢДЕУЛЕР ЖҮЙЕСІН ШЕШУДІҢ
САНДЫҚ ӘДІСТЕРІ

№1 – зертханалық жұмыс
Сызықты алгебралық теңдеулер жүйесін сандық шешудің тура әдістері

Сызықты алгебралық теңдеулер жүйесін (САТЖ) сандық шешудің 2 тәсілі
бар:
1. тура шешу;
2. жуықтап шешу;
Тура шешу тәсілі жүйенің шешімін саны шектеулі арифметикалық
операциялар көмегімен алуға мүмкіндік береді. Егер барлық операциялар дәл,
яғни есептеу қателігінсіз жүргізілсе, тура шешім алынады. Тура тәсілдерге
Крамер, Гаусс, Жордан-Гаусс, квадрат түбірлер әдістері жатады. Бұл әдістер
103 жоғары емес сандармен ЭЕМ көмегімен САТЖ-ның дәл шешімін анықтайды.
Жуықтап шешу тәсілдері итерациялық әдістер деп аталады. Олар жүйе
шешімін біртіндеп жуықтау шегі ретінде анықтайды. Оларға жататын әдістер:
Зейдель, қарапайым итерация, релаксация, градиентті т.б. Практикада бұл
әдістерді 106 ретті сандармен есептеу жүргізуде қолданады.
САТЖ-ны шешу үшін оның жалпы шешімі қай уақытта бар болады, және неше
шешімі болуы мүмкін деген сұрақтарға жауап беру керек ([8] қараңыз).
N белгісізді m теңдеуден тұратын САТЖ-ны қарастырайық:
(3.1)

немесе векторлық-матрицалық түрде жазсақ:
Ax=b (3.2)
Мұндағы А-коэффициенттерден құралған матрица, х- белгісіздерден құралған
вектор, b – бос мүшелерден құралған вектор.

1-анықтама: (3.1)- жүйенің шешімі деп реттелген, жүйенің барлық
теңдеулерін дұрыс теңдікке айналдыратын
х1=с1, х2=с2, ..., xn=cn сандар жиынын айтады.

2-анықтама: САТЖ бірлескен жүйе ([1] қараңыз) деп аталады, егер оның
ең болмағанда бір шешімі бар болса. Егер шешімі болмаса
жүйені қайшылықты немесе бірлестірілмеген жүйе дейді.

3-анықтама: Бірлескен жүйе анықталған деп аталады, егер оның шешімі
жалғыз болса, ал егер шешімі көп болса, оны анықталмаған
жүйе деп атайды.

4-анықтама: Теңсалмақты жүйелер деп бірінің шешімі екіншісінің де
шешімі бола алатын жүйелерді айтады.

5-анықтама: А-коэффициенттерден құралған матрицаға босмүшелерді
біріктіріп құрған матрицаны кеңейтілген матрица деп
атайды:

6-анықтама: Егер А матрицасының рангы В матрицасының рангыне тең
болса (rangA=rangB), онда (3.1)-жүйенің жалғыз шешімі бар
болады.

7-анықтама: Егер А матрицасының рангы белгісіздер санына тең болса
(r=n), онда (3.1)-жүйенің жалғыз шешімі бар болады ([1]
қараңыз).

8-анықтама: Егер А матрицасының рангы белгісіздер санынан кіші
болса (rn), онда (3.1)-жүйенің шешімі шексіз көп болады.

9-анықтама: Егер квадрат (текше) А матрицасының анықтауышы нөлден
өзгеше болса (detA0), онда А матрицасы ерекше емес
деп аталады.

10-анықтама: (3.1)-жүйенің матрицасы ерекше емес немесе айқындалмаған
болса, онда жүйе бірлескен жүйе деп аталады және шешімі
жалғыз болады.

Ерекше емес матрицалар үшін кері матрица ұғымы маңызды роль атқарады:

11-анықтама: , яғни А матрицасының екі жағынан да
көбейткен кезде бірлік матрица беретін матрицаны А
матрицасына кері матрица деп атайды және оны А-1 деп
белгілейді.

12-анықтама: Транспонирленген матрица деп сәйкес жолы мен бағаны
ауыстырылған матрицаны айтады: немесе
.

13-анықтама: Матрица ортогональды деп аталады, егер әр баған
элементтерінің квадраттарының қосындысы бірге, әр түрлі
бағанда орналасқан сәйкес элементтердің көбейтіндісінің
қосындысы нөлге тең болса. Немесе АТ*А=Е.

14-анықтама: А квадрат матрицасы өзінің транспонирленген
матрицасына тең болса, оны симметриялы матрица деп
атайды: А = АТ.

15-анықтама: А матрицасының характеристикалық теңдеуі деп
теңдеуін айтады. Немесе:
.

16-анықтама: Характеристикалық теңдеудің түбірлері () А
матрицасының меншікті мәндері деп аталады.

17-анықтама: А матрицасының меншікті мәндерін
қанағаттандыратын меншікті векторы деп теңдеуін
қанағаттандыратын векторын айтады.
18-анықтама: Егер detA=0 болса, онда жүйенің шешімі шексіз көп
болады.
Жоғарыда келтірілген анықтамаларды қолданып берілген жүйенің
қасиеттерін анықтап, шешімінің бар және жалғыз екендігіне көз жеткізгеннен
кейін оны шешудің әдістерін таңдауға болады.

Тура шешу тәсілдері
Гаусс әдісі

(3.3)
(3.3) - квадрат матрицалы жүйе берілсін. Жүйенің матрицасы ерекше емес
немесе айқындалмаған болсын. Гаусс әдісін практикада белгісіздерді
біртіндеп жою әдісі деп те атайды.
Әдістің негізгі идеясы немесе мағынасы ([12],[13] қараңыз): берілген
жүйенің матрицасын үшбұрышты түрге келтіру, бұл – тура жол деп аталады,
сосын үшбұрышты матрицаны қолданып құрған жаңа жүйеден белгісіздерді
біртіндеп табу, бұл – кері жол деп аталады. Сонда Гаусс әдісі 2 этаптан
тұрады:
1. тура жол – матрицаны үшбұрышты түрге келтіру.
2. кері жол – белгісіздерді ең соңғысынан бастап кері қарай табу.
Бұл әдіс тура тәсілге жатады. Яғни белгісіздердің мәнін бастапқы
жүйеге қойғанда теңдіктің оң жағындағы мәндер мен сол жағындағы мәндер бір
біріне тең болады.
Матрицаны үшбұрышты түрге келтіру әр түрлі әдіспен орындалады,
қолданылатын әдіс теңдеулердің коэффициенттеріне байланысты.
1.1 Тура жол
басшы элементі нөлден өзгеше деп есептеп (3.3)- жүйенің бірінші
теңдеуінің коэффициенттерін басшы элементке бөлу арқылы келесі теңдеуді
аламыз:
(3.4.)
Мұндағы
, (3.5)
(3.4) - теңдеуді қолданып (3.3) - жүйенің 2-ші теңдеуінен, 3-ші теңдеуінен
және n-ші теңдеуінен х1 белгісізін жоюға болады. Ол үшін (3.4)-ші теңдеуді
а21, а31, ..., аn1 коэффициенттеріне көбейтіп шыққан нәтижелерді сәйкесінше
2-ші теңдеуден, 3-ші теңдеуден, т.с.с. n-ші теңдеуден азайтып aij1 деп
белгілейміз:
(3.6)
Сонда келесідей жүйе аламыз:
(3.7)
Алынған (3.7) - жүйенің 1-ші теңдеуін а221 элементіне бөліп, теңдеу аламыз:
(3.8)
мұндағы
, (3.9)
х1 белгісізін қалай жойсақ, тура сол сияқты х2 белгісізін (3.7) - жүйеден
жоямыз, сонда мынадай жүйе алынады:
(3.10)
мұндағы
(3.11)
(3.10) - жүйенің 1-ші теңдеуін элементіне бөліп
(3.11)
теңдеу аламыз. Мұндағы
, (3.12)
(3.11) - теңдеу көмегімен (3.10) - жүйеден х3 белгісізін жоямыз.
Осы әрекеттер тізімін матрица толық үшбұрышты түрге келгенше
жалғастырамыз да (3.4)-ші, (3.8)-ші, (3.11)-ші, т.с.с. алуға болатын
теңдеулерді жинақтап келесідей жүйе аламыз:
(3.13)
1.2 Кері жол
(3.13) - жүйенің ең соңғы n-ші теңдеуінен белгісізін тауып алып
n-1 –ші теңдеуге қою арқылы xn-1 белгісізін табуға, сол сияқты кері қарай
барлық белгісіздерді табуға болады.
Ескерту: Бұл әдіс матрицаның басшы элементі нөлден өзгеше болған
жағдайда қолданылады. Егер берілген жүйе матрицасының басшы элементі нөлге
тең болса, жүйенің теңдеулерінің орындарын ауыстыру арқылы, арифметикалық
операциялар қолдану арқылы басшы элементтің нөлдігінен құтылуға болады.
Практикада есептеу жеңіл болуы үшін Гаусс компактілі схемасын
толтырады (1-кесте ), мысал үшін 4 белгісізді жүйе қарастырылды.

1-мысал:
(3.14)
Тура жол
Есептеу процесінің қалай өрбитінін бақылау үшін кесте толтырған дұрыс
(3-кестені қараңыз). Кестенің I - бөлігіне жүйенің кеңейтілген матрицасын
толтырамыз.
Кестенің соңғы екі бағаны ∑, S – есептеу қателігін бақылауды
ұйымдастырады. I – бөліктің ең соңғы бақылаушы бағанындағы мәндер
матрицаның әр жолындағы элементтердің қосындысы ретінде табылады . b1j
жолының бақылаушы бағанындағы элементтер I – бөліктің ең соңғы бақылаушы
бағанындағы мәндерді басшы элементке бөлу арқылы табылады . II –
бөліктің бақылаушы бағанындағы мәндер I – бөліктің ең соңғы бақылаушы
бағанындағы мәндерге (3.6) - формуланы қолдану арқылы анықталады . Дәл
осылай бақылаушы бағанның қалған екі жолын да толтыруға болады:
, төменде көрсетілген , формулалары арқылы. ∑, S –
бағандарындағы мәндер бір - бірінен өте аз ауытқуы немесе тұтас беттесуі
керек. Сонда есеп дұрыс жүргізілген болады. (3.5) - формуланы қолданамыз:
; ; ;
;
Бұл мәндерді кестенің b1j жолына жазамыз. (3.6) - формуланы қолданамыз:
;
;
; Бұл сандарды кестенің II – бөлігіндегі сәйкес орындарына жазамыз.
(Бұл мән кестенің ∑ бағанында орналасады.)
;
;
; Бұл сандарды кестенің II – бөлігіндегі сәйкес орындарына жазамыз.
; (Бұл мән кестенің ∑ бағанында орналасады.) (3.7) - формуланы
қолданамыз:
; ; ;
Бұл сандарды кестенің b2j жолына жазамыз. (3.11) - формуланы қолданамыз:
;

2-кесте – Гаусстың компактілі схемасы

Бөліктеi X1 X2 X3 X4 bi ∑=ai6
р
I 1 a11 a12 a13 a14 b1

2 a21 a22 a23 a24 b2

3 a31 a32 a33 a34 b3

4 a41 a42 a43 a44 b4
B1j 1 1 b12 b13 b14 b15
II 2

3

4
B2j 2 1 b23 b24 b25
III 3

4
B3j 3 1 b34 b35
IV 4
V 1 x4
1 x3
x2
1 x1
1

; Бұл сандарды кестенің III – бөлігіне толтырамыз.
(Бұл мән кестенің ∑ бағанында орналасады.)
Осы арада тура жол аяқталады, матрица үшбұрышты түрге келеді.
Кері жол
b1j, b2j және кестенің ең соңғы жолында орналасқан элементтерді
қолданып жүйе құрамыз:

Бұл жүйеден х3=-2,2779; х2=-2,9636; х1=-0,6583 екендігі шығады.

3- кесте – (3.14) - есептің кестелік алгоритмі

Бөліктер i X1 X2 X3 bi ∑ S
I 1 0.14 0.24 -0.84 1.11 0,65
2 1.07 -0.83 0.56 0.48 1,28
3 0.64 0.43 -0.38 -0.83 -0,14
B1j 1 1 1.7143 -6.0000 7.9286 4,6428 4.6428
II 2 -2.66436.98 -8.0036-3.6878-3.6879
3 -0.66723.4600 -5.9043-3.1114-3.1115
B2j 2 1 -2.6198 3.0040 1.3842 1.3842
III 3 1.7121 -3.9000-2.1879-2.1879

Гаусстың басшы элементті таңдау әдісі

Бұл әдісті қолдану үшін жүйенің матрицасының басшы элементтері немесе
диагональ элементтері нөлден өзгеше болуы керек ([11] қараңыз). Егер
матрицаның басшы элементтері нөлге тең болса, қандай да бір алмастырулар,
ауыстырулар қолдану арқылы нөлден құтылады. Жордан - Гаусс әдісін
сондықтан басшы элементті таңдау әдісі деп те атайды. Әдістің негізгі
идеясы модулі бойынша ең үлкен элементті басшы элемент деп алып, сол
элемент орналасқан жолдағы сәйкес белгісізді жою. Бұл әдіс те тура және
кері жолдан тұрады. Келесі жүйе берілсін.
(3.15)

Тура жол
1 (3.15) – жүйенің кеңейтілген матрицасын құрамыз.
элементтерінің арасынан модулі бойынша ең үлкен элементті басшы
элемент деп тағайындаймыз. Оны apq деп белгілейік. Барлық
мәндері үшін
(3.16)
көбейткішін есептейміз.
2 Әрбір басшы емес жолдан көбейткішіне көбейтілген басшы жол
элементтерін мүшелеп шегереміз:
(3.17)
Сонда q-шы бағанның басшы элементтен басқа элементтері нөлге айналады.
3 q-шы баған және басшы жолды тастап кетіп жаңа М1 матрица аласыз.
Бастапқы матрицаның бағаны мен жол саны азаяды.
4 М1 матрицасына бастапқы пункттерді қайталап қолдану арқылы М2
матрицасын аламыз.
5 Осы процессті бір белгісізді бір жолдан тұратын теңдеу қалғанша
жалғастырамыз.
6 Тастап кеткен басшы жолдардан жаңа жүйе құрастырамыз.

Кері жол

Басшы жолдардан құралған матрицаны әлдебір ауыстырулар арқылы
үшбұрышты түрге келтіріп, ең соңғы теңдеуден ең соңғы белгісізді, оны
қолданып оның алдындағы белгісізді, т.с.с. барлық белгісіздерді кері
бағытта анықтаймыз.
сандары қаншалықты азайған сайын есептеу қателігі де азаяды.
Сондықтан ЭЕМ-ді қолданып есептеу уақытында осы әдіс тиімді деп есептеледі.

Ескерту. Егер жүйе өте көп белгісіздерден тұрып, оның барлық
элементтерінің арасынан модулі бойынша үлкен элементті табу қиынға соқса
басшы жол ретінде жүйенің бірінші жолын, ал басшы элемент ретінде осы
жолдың модулі бойынша ең үлкен элементін алуға болады.
2-мысал:
(3.18)
Есептеу қадамдарының нәтижелерін 4- кестеге толтыруға болады:

Тура жол

а44=1,2671 басшы элемент болады. 4-жол басшы жол деп аталады.
1. (3.16) - формула көмегімен mi, i=1,2,3 мәндерін анықтаймыз:

4- кесте – (3.18) – есептің кестелік алгоритмі

БөліктеI mi X1 X2 X3 X4 Ai5
р
I 1 0.11759 1.1161 0.1254 0.1397 0.1490 1.5471
2 0.14766 0.1582 1.1675 0.1768 0.1871 1.6471
3 0.17923 0.1968 0.2071 1.2168 0.2271 1.7471
4 0.2368 0.2471 0.2568 1.2671 1.8471
II 1 0.09353 1.08825 0.09634 0.10950 1.32990
2 0.11862 0.12323 1.13101 0.13888 1.37436
3 0.15436 0.16281 1.177077 1.41604
III 1 0.07296 1.07381 0.08111 1.19746
2 0.10492 1.11170 1.20639

IV 1 1.06616 1.10944

2. (3.17) – формула бойынша басшы бағанда орналасқан басшы элементтен
өзге элементтерді нөлге айналдырамыз да қалған жаңа элементтерді
табамыз:
i=1; j=1 болғанда

i=1; j=2 болғанда

i=1; j=3 болғанда

i=1; j=4 болғанда

i=1; j=5 болғанда

i=2; j=1 болғанда

i=2; j=2 болғанда

i=2; j=3 болғанда

i=2; j=4 болғанда

i=2; j=5 болғанда

i=3; j=1 болғанда

i=3; j=2 болғанда

i=3; j=3 болғанда

i=3; j=4 болғанда

i=3; j=5 болғанда

Табылған элементтерден жаңа матрица құрып кестенің II-бөлігіне толтырамыз.
3. Жаңа матрицадан модулі бойынша үлкен элементті табамыз: ол - .
3-жолды басшы жол деп аламыз да жаңа көбейткіштерді анықтаймыз:

4. 2-пункттегі сияқты (3.17) – формула бойынша басшы бағанда
орналасқан басшы элементтен өзге элементтерді нөлге айналдырамыз да
қалған жаңа элементтерді тауып тағы жаңа матрица құраймыз:
5.
6. Осы жаңа матрицадан модулі бойынша үлкені . Тағы көбейткішті
есептейміз: .
7. 2-пункттегі сияқты (3.17) – формула бойынша басшы бағанда
орналасқан басшы элементтен өзге элементтерді нөлге айналдырамыз да
қалған жаңа элементтерді тауып тағы жаңа матрица құраймыз:
;

Кері жол

Кестеде қоршалған басшы элементтер орналасқан жолдардан жүйе құрамыз:

Белгісіздерді біртіндеп табамыз:
X1=1.04059
X2=0.98697
X3=0.93505
X4=0.88130.

Квадрат түбірлер әдісі
(3.19)
Жүйенің матрицасы симметриялы элементтерден тұратын болса, онда мұндай
жүйеге квадрат түбірлер әдісі қолданылады. Әдістің мақсаты ([13] қараңыз)
берілген матрицаны бір-біріне түйіндес екі үшбұрыш матрицаның көбейтіндісі
түріне келтірейік.
A=S*DS (3.20)
мұндағы S*- төменгі үшбұрышты матрица, S- жоғарғы үшбұрышты матрица .

SS*D матрицасын бір-біріне көбейтіп элементтерін А матрицасының
элементтеріне теңестіреміз. Алынған матрицасының диоганалдық элементтері
мына формуламен есептелінеді.

ал қалған элементтер үшін мына формула қолданылады:

(3.21)
(3.22)
(3.23)
(3.24)
(3.25)
Егер берілген матрицаның коэффициенті нақты және бас минорлары оң болса,
онда d матрицасын бірлік матрица деп, есептеу мына фолмулалармен
жүргізіледі:
(3.21*)
(3.22*)

(3.23*)
(3. 24*)
(3.25*)
Бұл формулаларды қолданғаннан кейін шыққан матрицаны мынадай үшбұрышты
жүйе құрамыз:
(3.26)
(3.27)
(3.28)
(3.29)
(3.30)
Практикада бұл әдіс 5-кестені толтырады.

немесе матрицалық –векторлық түрде:

5-кесте – Квадрат түбірлер әдісінің схемасы
i x1 x2 x3 bi
1 A11 a12 a13 b1
2 A21 a22 a23 b2
3 A31 a32 a33 b3
У1 У2 У3 bi
1 110 0 b1
2 12220 b2
3 132333 b3
x1 x2 x3 yi
1 S11 S21 S31 y1
2 0 S22 S32 y2
3 0 0 S33 y3

Ал үшбұрышты түрге келтірілген жүйенің белгісіздері қарапайым табылады.

3-мысал

e=0.5*10-3
Жүйе симметриялы элементтерден тұрады, яғни квадрат түрбірлер әдісін
қолдануға болады:
(3.21*) - формула бойынша:

(3.22*)-формула бойынша : ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.