Анықталмаған теңдеулерді шешудің жаңа әдістері: анықтауыштар арқылы n-ші дәрежелі теңдеулерді жүйеге келтіру және шешу


Қазақстан Республикасы
Білім және Ғылым Министрлігі
Анықталмаған теңдеулерді шешудің жаңа әдістері
Аннотация
«Анықталмаған теңдеулерді шешудің жаңа әдістері» тақырыбындағы жазылған ғылыми - ізденіс жұмысында анықталған және анықталмаған теңдеулер арасындағы байланыс, анықталған теңдеулер жүйесін анықталмаған теңдеуге келтіру және керісінше, анықталған және анықталмаған теңдеуді және анықталмаған теңдеулер жүйесін шешудің анықтауыш әдісі мен шешу жолдары іздестіріліп, қорытындыланып, мысалдар арқылы дәлелденген, анықталмаған теңдеудің бүтін шешімдерін және өзге де шешімдерін табудың жаңа әдістері қарастырылып, қорытындысы жасалған.
Аннотация
Научно-исследовательская работа на тему «Новые методы решения неопределенных уравнений» является ценной научно-обоснованной методической новинкой в решении определенных и неопределенных уравнений.
Вместе с тем, в поисковой работе сделан глубокий анализ решения системы определенных уравнений в неопределенные и, наоборот, определенные и неопределенные уравнения и систему неопределенных уравнений с использованием определителей и методов решения и доказаны на примере решенных задач.
Annotation
The research work on a theme " New methods of the decision of the uncertain equations " is a valuable scientifically - is proved methodical novelty in the decision of the certain and uncertain equations.
At the same time, in search work the deep analysis of the decision of system of the certain equations in uncertain and, on the contrary is made, the certain and uncertain equations and system of the uncertain equations with use of determinants and methods of the decision and are proved on an example of the decided tasks.
Пікір
Зерттеушінің «Анықталмаған теңдеулерді шешудің жаңа әдістері» тақырыбындағы ғылыми жұмысы көпмүшелер теориясының негізгі мәліметтерінің бірі болған теңдеулер теориясына қатысты жазылған. Ғылыми жұмыста n-ші дәрежелі теңдеулерді шешу жаңаша көзқарас тұрғысында баяндалған.
Олар:
- анықталған және анықталмаған теңдеулерді шешу;
- анықталмаған теңдеулерді анықтауыш әдісімен шешу;
- n-ші дәрежелі анықталған теңдеулерді анықтауыш әдісімен шешу;
- жоғары дәрежелі теңдеуді шешудің жаңа әдістері т. с. с.
Зерттеу жұмыстарының ғылыми жаңалығы өте құнды. Жаңа әдіспен жоғары дәрежелі теңдеулердің түбірлерін есептеу теориясы берілген және зерттеушілер өз әдістерін мысалдар арқылы дәлелдеген. Анықталған және анықталмаған теңдеулерді шешуде зерттеушілердің өз талдауы, өз болжамы берілген, сондықтан еңбектің маңызы зор.
Сол себепті ғылыми жұмысты байқауға жіберуге болады.
Мазмұны
I. Кіріспе . . .
1. Мақсаты мен міндеті
2. Зерттеу жаңалығы
II. Негізгі бөлім: . . .
- Теңдеулер жүйесін анықталмаған теңдеулерге келтіру әдістері.
- Анықталмаған теңдеуді теңдеулер жүйесіне келтіру.
- Теңдеулер жүйесін Крамер әдісімен (анықтауыштар әдісімен) шешу.
- Есептеудегі жаңалықтар тізбесі:
n - ші дәрежелі анықталмаған теңдеулерді теңдеулер жүйесіне ауыстыру және оны шешудің ерекше жолдары.
- Анықталмаған теңдеуді анықтауыштар әдісімен шешу және мысалдар арқылы дәлелдеу.
- Анықталмаған теңдеулер жүйесін анықтауыштар әдісімен шешу жолдары.
- Анықталған теңдеуді (квадрат теңдеуді) анықтауыштар әдісімен шешу.
- Жоғары дәрежелі теңдеулерді анықтауыш әдісімен шешу жолдарын іздестіру
III. Қорытынды: . . .
Зерттеу жұмысын есептер шығаруда қолдану-
дың мәні
IV. Пайдаланған әдебиеттер тізімі . . .
. . .
Кіріспе
Математика оқулықтарында кездесетін алгебралық теңдеулерді екі үлкен топқа бөлуге болады :
1. Анықталған теңдеулер
- Анықталмаған теңдеулер.
Анықтама 1.
Теңдеулер саны мен айнымалылар саны тең болған теңдеулер анықталған, керісінше тең болмаса анықталмаған теңдеулер деп аталады.
Мысалы :
а 1 х + а 0 = 0 ( 1 )
а 2 х 2 + а 1 х + а 0 = 0 ( 2 )
а 3 х 3 + а 2 х 2 + а 1 х + а 0 = 0 ( 3 )
а 4 х 4 + а 3 х 3 + а 2 х 2 + а 1 х + а 0 = 0 т. с. с. ( 4 )
теңдеулер анықталған,
ал төмендегі теңдеулер анықталмаған теңдеулер деп аталады.
а 1 х + а 2 у + а 3 = 0 ( 1 / )
а 1 х 2 + а 2 ху + а 3 у 2 + а 4 х + а 5 у + а 6 =0 ( 2 / )
а 1 х 3 + а 2 х 2 у 2 + а 3 ху + а 4 у 3 = 0 ( 3 / )
Яғни, екі және одан да көп айнымалылары бар теңдеулерді анықталмаған теңдеулер деп атайды. Анықталмаған теңдеудің шешімі деп осы теңдеуді қанағаттандыратын айнымалылар мәндерінің барлық жиынын айтады. Анықталмаған теңдеулерді ежелгі грек ғалымы Диофант (б. э. III ғ. ) өзінің 13 кітаптан тұратын (бұлардың алғашқы алтауы ғана сақталған) «Арифметика» деп аталатын еңбектерінде қарастырған. Сондықтан анықталмаған теңдеулер теориясын Диофанттың анализі деп айтады.
Математикада 1, 2, 3, 4 теңдеулерді шешудің ( радикалдарда ) жалпы әдістері табылған, бірақ, бесінші және одан жоғары теңдеулердің шешу әдістері әлі күнге дейін белгісіз. Сонымен бірге анықталмаған теңдеулерді шешудің жалпы әдістері қаралмаған. Міне осы мақсатта төмендегі ғылыми зерттеу жұмысы жүргізілді .
Жұмыста :
- Анықталған және анықталмаған теңдеулердің бір-біріне тығыз байланыстылығы бар екендігін дәлелдедік.
- Анықталған теңдеулер жүйесінен анықталмаған теңдеулерге өту және керісінше ауыстырулар жасау ерекшеліктерін баяндадық.
- Анықталған және анықталмаған теңдеулерді шешудің анықтауыш әдістерін қарастырдық.
- Жоғары дәрежелі теңдеулердің шешімдерін табудың жаңа әдістерін және аса маңызды қорытындыларын шығардық.
Ғылыми жұмыс мынадай жоспарда жүргізілген :
I. Теңдеулер жүйесін анықталмаған теңдеулерге келтіру әдістері.
II. Анықталмаған теңдеуді теңдеулер жүйесіне келтіру.
III. Теңдеулер жүйесін Крамер әдісімен (анықтауыштар әдісімен) шешу.
IV. Есептеудегі жаңалықтар тізбесі:
n - ші дәрежелі анықталмаған теңдеулерді теңдеулер жүйесіне ауыстыру және оның ерекше жолдары.
V. Анықталмаған теңдеуді анықтауыштар әдісімен шешу және мысалдар арқылы дәлелдеу.
VI. Анықталмаған теңдеулер жүйесін анықтауыштар әдісімен шешу жолдары.
VII. Анықталған теңдеуді (квадрат теңдеуді) анықтауыштар әдісімен шешу.
VIII. Жоғары дәрежелі теңдеулерді анықтауыш әдісімен шешу жолдарын іздестіру
Қорытынды: . . .
Зерттеу жұмысын есептер шығаруда қолдану-
дың мәні
Пайдаланған әдебиеттер тізімі . . .
. . .
1-тарау. Теңдеулер жүйесін анықталмаған теңдеулерге келтіру
әдістері.
(3) а 1 х + в 1 у = c 1
a 2 x + b 2 y = c 2
теңдеулер жүйесін қосу немесе азайту арқылы мынадай анықталмаған теңдеуге келтіруге болады:
( а 1 + а 2 ) х + ( в 1 + в 2 ) у = c 1 + c 2 мұнда а 1 + а 2 = a, в 1 + в 2 = в, с 1 + с 2 = с
деп алсақ,
ах + ву = с (4) анықталмаған теңдеу келіп шығады.
а )
(3) теңдеулер жүйесі мен (4) анықталмаған теңдеулерді шешудің ортақ әдісін табуға бола ма? деген сұраққа жауап беру үшін осыларды шешу әдістерін қарастырайық.
(3) теңдеулер жүйесін шешудің бірнеше әдістері бар. Ол мектеп курсынан белгілі болған қосу тәсілі, алмастыру тәсілі, тағы да анықтауыш әдісі, жоғарғы математикадағы Крамер әдісі, белгісіздерді жоғалту әдісі ( Гаусс әдісі ) .
б )
(4) Анықталмаған теңдеудің бүтін шешімін табуды қарастырайық.
ах + ву + с = 0 ( 4 1 ) теңдеуінде d = ( а, в ) болғанда, теңдікті d-ға бөліп,
с / d = c 1 , деп алатын болсақ
а 1 х + в 1 у + с 1 = 0 теңдеуі шығады.
Егер с = 0 деп алсақ, ах + ву = 0 болады.
Теорема 2:
Егер а және в өзара жай сандар және ( х 0 ; у 0 ), ах + bу + с = 0 (4 1 ) теңдеуінің дербес түбірі болса, онда t = 0, ±1, ±2, . . . болғанда, х = х 0 - bt, y = y 0 + at ( 4 1 ) теңдеудің бүтін шешімдері болады.
Мысалы:
127х - 52у + 1 = 0 теңдеудің дербес шешімі х = 9, у = 22 болады.
Олай болса, ( t=0, ±1, ±2, . . . ) болғанда
х = 9+52t,
y = 22+127t теңдеудің барлық бүтін шешімдері болады.
Анықталмаған теңдеудің бүтін шешімдерін табу, оның дербес шешімін табуға келіп тірелді. Осы дербес ( х 0 ; у 0 ) түбірді оңай, жылдам табу жолын қарастырайық.
Жоғарғы сыныптың алгебра курсында бұл анықталмаған теңдеулердің бүтін шешімін табудың шектеусіз бөлшектер әдісі қолданылады.
Ол әдісті Евклид алгоритмі жәрдемінде лайықты бөлшектер арқылы келтіріп шығаруға болады.
Теорема 3:
Егер ( х 0 ; у 0 ) ах + by + c = 0, ( a, b ) = 1 болғандағы теңдеудің дербес бүтін түбірі болса,
х 0 = ( -1 ) n-1 ·c·Q n-1 ,
y 0 =( -1 ) n ·c·p n-1
болады, ал жалпы түбірлері
х = ( -1 ) n-1 ·c·Q n-1 - bt
y = ( -1 ) n ·c·p n-1 + at ( t = 0, ± 1, ± 2 . . . , ал p n-1 пен Q n-1 лайықты бөлшектер) .
Сандар теориясы курсында ах + by = c түріндегі қарапайым анықталмаған теңдеулер мен х 2 - Dy 2 = ±1 Пелль теңдеулерін шешу әдістері қарастырылады.
Осындай теңдеулерді шешудің жоғарыдағы теореманы қолдану әдісін келтірейік:
Мысалы : 91х + 27у = 11
теңдеуінің бүтін шешімдерін табайық
мұнда
а = 91 b = 27 болғандықтан,
91/27 = 3, 2, 1, 2, 3 .
Лайықты бөлшектердің мәнін біртіндеп табайық :
P 0 /Q 0 = 3/1=3,
p 1 /Q 1 = 7/2,
p 2 /Q 2 = 10/3,
p 3 /Q 3 = 27/8,
P 4 /Q 4 = 91/27.
Демек, К = 4, p 3 = 27, Q 3 = 8 болғанда,
х 0 = ( -1 ) 4+1 ·11·8 = -88
у 0 = ( -1 ) 4 ·11·27 = 297 болады, олай болса,
х = -88 + 27t, y = 297 - 91t жалпы шешім болады.
2-тарау. Анықталмаған теңдеулерді теңдеулер жүйесіне келтіру әдістері.
с )
Енді Пелль теңдеуіне көшейік x 2 - Dy 2 = 1 (5)
Пьер Ферма бұл теңдеудің бүтін санды шешімін қарастыра отырып, мүмкін болған жағдайда сансыз көп бүтін шешімдері болатындығын көрсеткен. Сондықтан да (5) теңдеуді Ферма теңдеуі деп атаған жөн.
Алдын ала D бір санның квадратына тең болсын деп алсақ, (5) - теңдеу х 2 + t 2 = 1 теңдеуге
болғанда айналады. Ал кез-келген х 2 + у 2 = z 2 теңдеудің шешімін Пифагор үшбұрышын пайдаланып табуға болады.
Мысалы :
х = 3, y = 4, z = 5
д )
Егер х 2 - Dy 2 = 1 ( 5 ) теңдеуінде D = d 2 болса, онда оны
х 2 - d 2 y 2 = ( x + dy ) ( x - dy )
болғандықтан сызықты теңдеулер жүйесіне жіктеуге болады, яғни
х + dy = 1 х + dy = -1
x - dy = 1 немесе x - dy = -1
x = 1, y = 0 бірінші жүйенің, ал
х = -1, y = 0 екінші жүйенің шешімі болады.
Ал берілген (5) теңдеудің х = ± 1, y = 0 болғанда ғана бүтін шешімі болады.
е ) x 2 + 2y 2 = z 2
теңдеуінің бүтін шешімін табу және оның ерекшеліктері
 x
2
+ 2y
2
= z
2
теңдеуінде ( x, y, z ) = 1 деп алайық, мұнан
x
2
+ 2y
2
= z
2
теңдеуінде ( x, y, z ) = 1 деп алайық, мұнан
2y 2 =z 2 - x 2 = ( z + x ) ( z - x )
z + x = kd
z - x = ed Мұндағы k және е - бүтін cандар
2z = d( k + e )
2x = d( k - e ) ( z, x ) = 1 болғаны үшін, d= 2
Сол себепті z + x пен
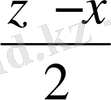 Equation. 3 өзара жай сан
Equation. 3 өзара жай сан
z + x = n 2
Олай болса ( 15 ) болады.
z - x = 2m 2
Егер
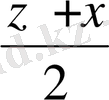 Equation. 3 мен ( z - x ) өзара жай сан болса,
Equation. 3 мен ( z - x ) өзара жай сан болса,
z + x = 2m 2
( 16 ) болады
z - x = n 2
Бұл жерде n және m - бүтін сан,
m - тақ сан және n > 0, m > 0.
Олай болса, теңдеулер жүйесін шешсек,
z =
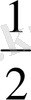 ( n
2
+ 2m
2
), x =
( n
2
+ 2m
2
), x =
 ( 2m
2
- n
2
), y = mn теңдігі пайда болады.
( 2m
2
- n
2
), y = mn теңдігі пайда болады.
Егер
n = 2b және m = a деп алатын болсақ,
х 2 + 2у 2 = z 2 теңдеудің шешімі
x = ±( a 2 + 2b 2 ),
y = 2ab,
z = a 2 + 2b 2 ( 17 ) теңдеу болады.
Біз теңдеулер жүйесін анықталмаған теңдеулерге келтіру мүмкіндіктерін айтқан болатынбыз.
Мына, жоғарыдағы Ферма теңдеуін, x 2 + 2y 2 = z 2 теңдеуін теңдеулер жүйесіне келтіріп шешуге болатындығын, көрсеттік. Сөйтіп, қорыта айтқанда, анықталмаған теңдеулерді теңдеулер жүйесіне келтіру мүмкін екен.
3-тарау. Теңдеулер жүйесін Крамер әдісімен (анықтауыштар әдісімен) шешу.
a 1 x+b 1 y=c 1
a 2 x+b 2 y=c 2 (6) теңдеулер жүйесін Крамер әдісімен шешу жоғарғы математика курсынан белгілі болғандықтан, оның формуласын келтірейік
a 1 b 1 c 1 b 1 a 1 c 1 ∆ = ∆ x = ∆ y =
a 2 b 2 c 2 b 2 a 2 c 2
Егер ∆ ≠ 0 болса, ( 6 ) теңдеудің шешімі х = ∆x/ ∆ , y = ∆ y/ ∆ формулалары арқылы табылады.
n - дәрежелі үш айнымалысы бар теңдеулер және оларды шешу.
Мынадай анықталмаған теңдеулерді шешудің жалпы формуласын келтірейік.
( бұл біздің жеке шешу әдісіміз болады )
а) х + у = z теңдеуін шешу үшін мына формулаларды пайдалануға болады :
1) х = 2n, y = 1 - n, z = n+1 (7) n = 0, 1, 2, . . . , болғанда бүтін шешімдері болады.
2) x = 2n, y = ( 1 - 2n ) /2, z = ( 2n + 1 ) /2 теңдіктерін пайдаланып, қалған шешімдерін табуға болады.
б) x 2 + y 2 = z 2 теңдеуінің шешімін табу үшін мынадай түрлендіруді орындаймыз :
( х + у ) 2 = х 2 + 2ху + у 2 формуласын пайдаланып, х 2 + у 2 = z 2 теңдеуін былай жазуға болады:
( х +у ) 2 - 2ху = z 2 . Бұл теңдеудегі x, y, z орнына (7) теңдіктегі мәндерін қойғанда:
4n 2 + 4n( 1 - n ) +(1 - n) 2 = ( 1 + n ) 2 теңдігін алуға болады. Осыдан мынадай формула
x 2 = 4n 2 , y 2 = 4n( 1 - n ) + (1 - n) 2 , z 2 = ( 1 + n ) 2 ( 8 ) келіп шығады.
Демек x 2 + y 2 = z 2 теңдеуінің шешімдері
x = 2n, y =
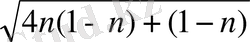 2
, z = 1 + n (8) болады.
2
, z = 1 + n (8) болады.
в) x 3 + y 3 = z 3 теңдеудің шешімдерін табайық, ол үшін
2n + ( 1 - n ) = n + 1 теңдігін пайдаланайық . Осы теңдікті куб дәрежеге шығарғанда,
( 2n ) 3 + 3*( 2n ) 2 *( 1 - n ) + 3*2n*( 1 - n ) 2 + ( 1 - n ) 3 = ( n + 1 ) 3 болады
Бұл теңдіктен x 3 = 8n 3
y 3 = 6n*( 1 - n 2 ) + ( 1 - n ) 3
z 3 = ( n + 1 ) 3 формулаларды табуға болады.
Олай болса, кез келген n > 2 үшін x n + y n = z n теңдеудің шешімдерін табуға болады.
г) x n + y n = z n
теңдеудің шешімдерін табу немесе Пьер Ферманның үлкен теоремасына ерекше жасалған жол .
Диофант Александрскийдің «Арифметика» кітабына жазылған Пьер Ферманның сонау «Мен мұны дәлелдеуді білемін, бірақ бос жай жетпегендіктен дәлелді келтірмедім» деген сөзіне әлі күнге дейін толық жауап берілмегені математиктерге белгілі жай .
Сол анықталмаған Ферма теңдеуін
x n + y n = z n n > 2 болғандағы шешудің жалпы жолын қарастырамыз.
x n = ( 2m ) k+1 , y n = 2m( k + 1 ) *( 1 - m k ) + ( 1 - m ) k+1 , z n = ( 1 + m) k+1 (10)
Мұндағы m
 ( -
( -
 ,
,
 ), n= 1, 2, 3, … k = 0, 1, 2, …
), n= 1, 2, 3, … k = 0, 1, 2, …
4-тарау. n-ші дәрежелі анықталған теңдеулерді теңдеулер
жүйесіне ауыстыру әдісі және оның ерекше жолдары.
a n x n + a n-1 x n-1 + … + a 1 x + a 0 = 0 ( 18 ) теңдеуді теңдеулер жүйесіне алмастыру мүмкін бе?
a n , a n-1 , …, a 0 коэффиценттері мен n - ші теңдеулер жүйесіне келтіру мәселесін қарастырайық. Элементар теңдеулерді шешуден бастайық.
Бәрімізге белгілі мына формулаларды басқаша шешумен салыстырайық.
ах + в = с ах 2 + вх + с = 0
х =
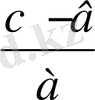 х
1, 2
=
х
1, 2
=
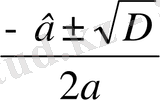
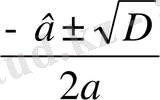
D = в 2 - 4ас т. с. с.
Мысалы :
- х2- 5х + 6 = 0
Виет формуласы бойынша х 1 = 3, х 2 = 2 шешімі табылады.
- х2- 5х + 6 = 0
Теңдеуді - Виет теоремасы бойынша, теңдеулер жүйесіне айналдыруға болады.
х 1 + х 2 = 5
х 1 ∙ х 2 = 6
Осы жүйенің коэфиценттерін алайық :
1 1 5
1 1 6
сандары пайда болады.
5 санын екі санның қосындысы түрінде былай жазуға болады .
5 = 1 + 4
5 = 2 + 3
6 санын екі санның көбейтіндісі түрінде былай жазуға болады :
6 = 1*6
6 = 2*3 Осы екеуінен жауаптың 2 және 3 болатындығын табуға болады.
3) x 2 - 5x + 6 = 0 теңдеуін анықтауыш әдісімен шешейік:
∆x 1 = 5 + 1 = 6
∆x 2 = 5 - 1 = 4
∆ = 2 * 1 = 2
x 1 = ∆x 1 ¦ ∆ = 6 ¦ 2 = 3
x 2 = ∆x 2 ¦ ∆ = 4 ¦ 2 = 2
Осы әдісті жалпылауға көшейік :
Математикалық рекурсия әдісін қолданайық:
а) ax 2 + bx + c = 0 болса, a = 1, b = -5, c = 6 болғанда,
x 1 = ∆x 1 ¦ ∆
∆x 1 = - b + 1
∆x 2 = - b - 1 x 2 = ∆x 2 ¦ ∆ болады екен
∆ = 2a
б) x 2 + px + q = 0 болғанда
∆x 1 = - p + 1
∆x 2 = - p - 1 x 1 = ∆x 1 ¦ ∆
∆ = 2 x 2 = ∆x 2 ¦ ∆
в) Виет теремасы бойынша
ах 2 + вх + с = 0
х
2
+
 x +
x +
 = 0, p =
= 0, p =
 Equation. 3,
Equation. 3,
 q =
q =
 Equation. 3
Equation. 3
x
1
+ x
2
= -
 Equation. 3
Equation. 3
x
1
∙ x
2
=
 Equation. 3 ( 19 )
Equation. 3 ( 19 )
г) ах 2 + вх + с = 0 теңдеуден мыналарды жазуға болады:
2
а ∆х 1 / ∆ + b ∆х 1 / ∆ + с = 0
2
а ∆х 2 / ∆ + в ∆х 2 / ∆ + с = 0 (20)
теңдеулер жүйесінен мына теңдікті табуға болады :
а( ∆х 1 ) 2 + в∙∆х 1 ∙∆ + с∆ 2
а( ∆х 2 ) 2 + в∙∆х 2 ∙∆ + с∆ 2 = 0 осы теңдіктерді қосатын болсақ:
а[( ∆х 1 ) 2 + ( ∆х 2 ) 2 ] + в∆( ∆х 1 +∆х 2 ) + 2с∆ 2 = 0
а( ∆х 1 + ∆х 2 ) 2 - 2а∆х 1 ∆х 2 + в∆( ∆х 1 + ∆х 2 ) + 2с∆ 2 = 0 ( 21 ) болады.
Егер азайтатын болсақ, онда:
а( ∆х 1 - ∆х 2 ) 2 + в∆( ∆х 1 +∆х 2 ) = 0 ( 22 ) болады.
( 19 ) теңдеулер жүйесінен :
х 1 ∙х 2 = ∆х 1 / ∆ * ∆х 2 / ∆ = ∆х 1 ∙∆х 2 / ∆ 2 =

а∙∆х 1 ∙∆х 2 = с∆ 2 ( 23 )
∆х 1 + ∆х 2 = -
∙∆ ( 24 ) теңдеулерді табуға болады.
Яғни (22) теңдіктен:
a( ∆x 1 - ∆x 2 ) + b∆( ∆x 1 - ∆x 2 ) = 0
( ∆x
1
- ∆x
2
)
 a( ∆x
1
- ∆x
2
) + b∆
a( ∆x
1
- ∆x
2
) + b∆
 = 0
= 0
∆x 1 - ∆x 2 = 0
a( ∆x 1 - ∆x 2 ) + b∆ = 0
∆ = ( ∆x 2 - ∆x 1 ) a / b (25) болады.
- берілген теңдеулер жүйесінің бірінші теңдеуінен :
a( ∆x 1 ) 2 + b( ∆x 1 ) * ( ∆x 2 - ∆x 1 ) a / b + c
( ∆x 2 - ∆x 1 ) a / b
2 = 0
a( ∆x 1 ) 2 + ∆x 1 ∆x 2 a - a( ∆x 1 ) 2 +
( ∆x 2 ) 2 - 2∆x 2 ∆x 1 + ( ∆x 1 ) 2
ca 2 / b 2 = 0
a∆x 1 ∆x 2 + ca 2 / b 2
( ∆x 2 ) 2 + 2∆x 2 ∆x 1 + ( ∆x 1 ) 2
= 0
a∆x 1 ∆x 2 + ca 2 / b 2 ( ∆x 1 + ∆x 2 ) 2 = 0, осыдан
∆x 1 ∆x 2 = - (∆x 1 + ∆x 2 ) 2 ca / b 2 (26)
(20) теңдеуінің екінші теңдігінен :
(26) теңдікті пайдаланып мыналарды табайық:
а∙( ∆х 2 ) 2 + в∙∆х 2 + с∆ 2 =0
а∙( ∆х 2 ) 2 + в∙∆х 2 ∙ а( ∆х 2 -∆х 1 ) / в + с∙ а 2 ( ∆х 2 -∆х 1 ) 2 / в 2 = 0
а∙( ∆х 2 ) 2 + а∆х 2 ( ∆х 2 - ∆х 1 ) +
( ∆х 2 - ∆х 1 ) 2 = 0
а∙ ∆х 2 2 + а∙ ∆х 2 2 - а∙∆х 1 ∙∆х 2 +
∆х 2 2 - 2
∆х 2 - ∆х 1 +
∆х 1 2 = 0
( 2а +
) ∆х 2 2 - ( а - 2
) ∆х 1 ∆х 2 +
∆х 1 2 = 0 ( 27 )
( 2а +
) ∆х 2 2 + (
- 2с 2 а 3 /в 4 ) ( ∆х 1 + ∆х 2 ) 2 +
( ∆х 1 ) 2 = 0 (27')
Міне осылай, (26) және ( 27 / ) теңдеулерден құралған теңдеулер жүйесін құрастыруға болады екен.
Яғни, ах 2 +вх+с=0 квадрат теңдеуі орнына мына теңдеулер жүйесін
шешуге болатындығын көреміз.
∆x 1 ∆x 2 = - ( ∆x 1 + ∆x 2 ) 2 ca / b 2 (26) (28)
( 2а +
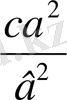 ) ∆х
2
2
- ( а - 2
) ∆х
2
2
- ( а - 2
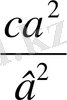 ) ∆х
1
∆х
2
+
) ∆х
1
∆х
2
+
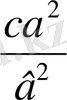 ∆х
1
2
= 0 (27)
∆х
1
2
= 0 (27)
Қорытынды :
Кез келген n- ші дәрежелі анықталған теңдеулерді шешуді, теңдеулер жүйесін шешуге келтіруге болады екен.
Мысалдар қарастырайық:
x 2 - 8x + 15 = 0 теңдеуін анықтауыш әдісімен шешейік. Теңдеулер жүйесіне айналдырсақ, ол былай болады:
x 1 + x 2 = 8
3x 1 - 4x 2 =3 Виет теоремасы мен іріктеу әдістері арқылы осы жүйені шығаруды жалғастырамыз.
Бұл системаны анықтауыш әдісімен шешейік:
1 1
∆ = = - 4 - 3 = - 7 ∆ = - 7
3 - 4
8 1
∆x 1 = = - 32 - 3 = - 35, ∆x 1 = - 35
3 - 4
1 8
∆x 2 = = 3 - 24 = - 21 ∆x 2 = - 21
3 3
x 1 = ∆x 1 / ∆ = - 35 / - 7 = 5 x 1 = 5
x 2 = ∆x 2 / ∆ = -21 / - 7 = 3 x 2 = 3
Жауабы: x 1 = 5, x 2 = 3
5-тарау. Анықталмаған теңдеулерді анықтауыш әдісімен шешу және мысалдар арқылы дәлелдеу
4-тарауда анықталған теңдеулерді теңдеулер жүйесіне келтіру мүмкіндігі туралы қорытынды шығарылды. 1-тарауда теңдеулер жүйесін анықталмаған теңдеулерге келтіру туралы айтылған болатын. Міне, осы тұжырымдардан кез-келген анықталмаған теңдеуді шешудің анықтауыш әдісін келтіріп шығаруға болады.
Осылардан пайдаланып, кейбір есептеудің дербес және жалпы түбірлерін табуға мысалдар келтірейік:
ax + by = c
мұндағы а, в, с - тұрақты
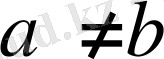 сандар.
сандар.
Осы теңдеуді анықтауыш әдісімен шешейік.
∆ = а - в болғанда,
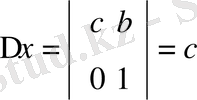 , ал
, ал
 болады. Сөйтіп теңдеудің дербес шешімі
болады. Сөйтіп теңдеудің дербес шешімі
x 0 = c / (a - b)
y 0 = - c / (a - b) болады.
Олай болса, оның жалпы шешімі
x = c / (a - b) + bt y= - c / (a - b) - at болатындығын табамыз.
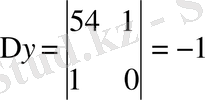
Мысал 1: 54x+37y=1
∆ = a - b = 54 - 37 = 17 ∆ = 17
∆
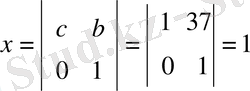 , ∆y =
, ∆y =
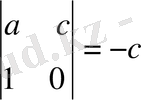 ,
,
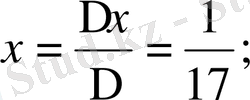 Equation. 3
Equation. 3
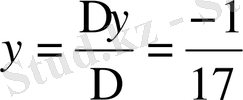 Equation. 3
Equation. 3
Тексеру:
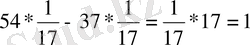
Жауабы: x = 1/17, y = - 1/17
Мысал 2: 27x-40y=1
∆ = 27 + 40 = 67
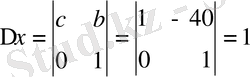 Equation. 3,
Equation. 3,
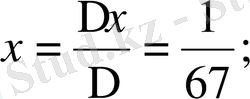 Equation. 3
Equation. 3
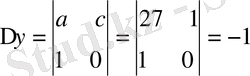 Equation. 3,
Equation. 3,
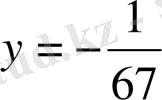 Equation. 3
Equation. 3
Тексеру:
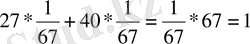
Жауабы: x = 1 / 67, y = - 1 / 67
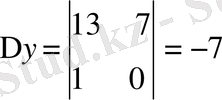
Мысал 3: 13x-15y=7
∆ = 13 - (-15) = 28
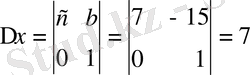 Equation. 3,
Equation. 3,
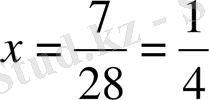 Equation. 3,
Equation. 3,
 Equation. 3,
Equation. 3,
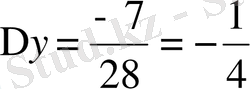 Equation. 3 .
Equation. 3 .
Тексеру:
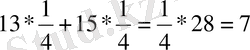 Equation. 3
Equation. 3
Жауабы: x = 1 / 4, y = - 1 / 4
Мысал 4: 253x-449y=3
∆ = 253 + 449 = 702
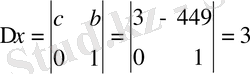 Equation. 3,
Equation. 3,
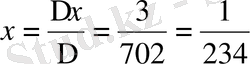 Equation. 3,
Equation. 3,
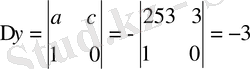 Equation. 3,
Equation. 3,
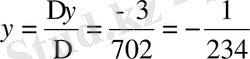 Equation. 3,
Equation. 3,
Тексеру:
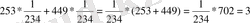 Equation. 3
Equation. 3
Жауабы: x = 1 / 234, y = - 1 / 234
6-тарау. Анықталмаған теңдеулер жүйесін анықтауыш
әдісімен шешу
1-әдіс:
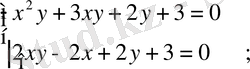
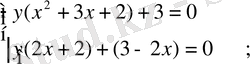
f(x) =
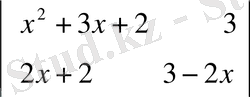 = 0,
= 0,
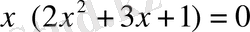 ,
,
x = 0 болғанда, y = -1. 5 ( 0; -1. 5 ), x = -0. 5 болғанда, y = - 4 ( -0. 5; -4 )
Жауабы: ( 0; -1. 5 ), ( -0. 5; -4 )
2-әдіс:
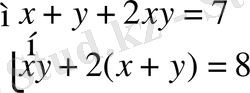 ,
,
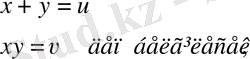
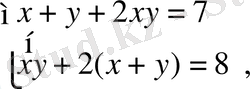
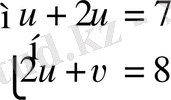 ∆ =
∆ =
 =
=
 = 1- 4 = - 3, ∆ = - 3.
= 1- 4 = - 3, ∆ = - 3.
∆u =
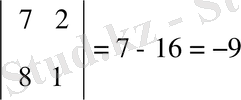 , ∆
, ∆
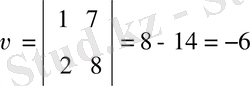 , u
, u
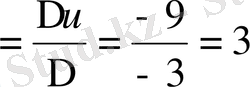 .
.
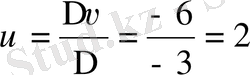
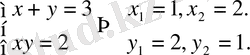 Жауабы: (1; 2), (2; 1)
Жауабы: (1; 2), (2; 1)
7-тарау. Анықталған теңдеуді (квадрат теңдеуді) анықтауыш әдісімен шешу
a 0 x 2 + a 1 x + a 2 = 0 теңдеуін a 0 = 1 болған жағдайдағы шешуді қарастырайық:
Мысал 1: x 2 - 8x + 15 = 0 болғанда,
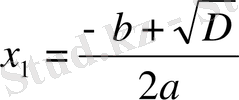 ,
,
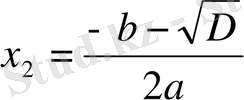 ,
,
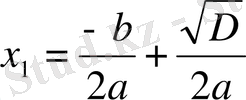
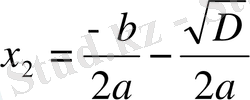 .
.
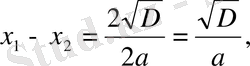
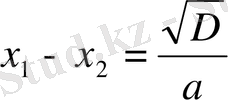 болатындығын табамыз.
болатындығын табамыз.
D=64 - 60=4
болғандықтан, Виет теоремасыменен
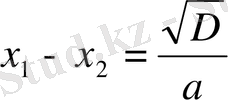 теңдігі бойынша,
теңдігі бойынша,
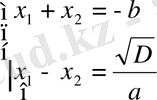 болады,
болады,
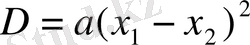
Сонда
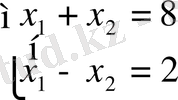 болғанда
болғанда
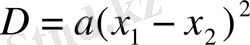
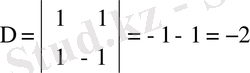
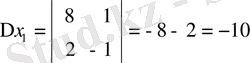
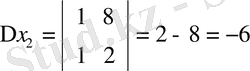
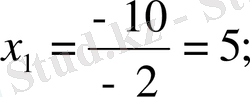
 ,
,
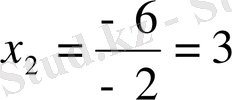 ;
;
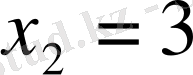 болады.
болады.
Жауабы:
 ,
,
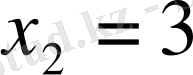
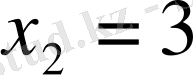
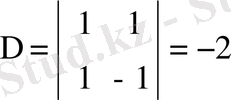
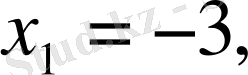
Мысал 2: x 2 + 12x + 27 = 0
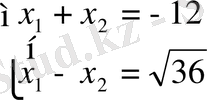 Equation. 3
D=144-108=36,
Equation. 3
D=144-108=36,
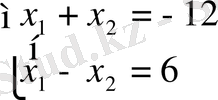 Equation. 3 ;
Equation. 3 ;
 Equation. 3,
Equation. 3,
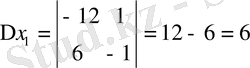 Equation. 3,
Equation. 3,
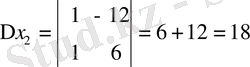 Equation. 3 .
Equation. 3 .
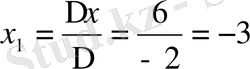 Equation. 3,
Equation. 3,
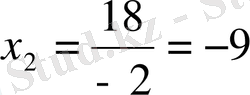 Equation. 3,
Equation. 3,
 Equation. 3
Equation. 3
Жауабы:
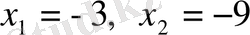
a
0
 1 болғандағы, a
0
x
2
+ a
1
x + a
2
= 0 (а) квадрат теңдеуді шешудің анықтауыш әдісін жалпылау арқылы келтіреміз.
1 болғандағы, a
0
x
2
+ a
1
x + a
2
= 0 (а) квадрат теңдеуді шешудің анықтауыш әдісін жалпылау арқылы келтіреміз.
Виет теоремасы бойынша:
x 1 + x 2 = -a 1 /a 0 (б)
x 1 x 2 = a 2 /a 0 Ал дискриманттың мынадай жаңа түрін таптық
D = a 0 2 (x 2 - x 1 ) (с) . (б) және (с) лардан:
x 2 - x 1 = D / a 0 2 a 0 2 x 2 - a 0 2 x 1 = D
Мұнан,
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz