Иррационал сандар: Дедекиндше қима, қасиеттері және иррационал теңдеулерді шешу әдістері


ИРРАЦИОНАЛ САН ҰҒЫМЫ
Иррационал сан де қандай санды айтады? Міне, осы санның анықтамасын берейік. Иррационал санды анықтауда үш түрлі көзқарас бар; бұлардың барлығына бірдей тоқтамай, біреуін ғана қарастырамыз. Ол - иррационал санның Дедекиндше анықтамасы.
Барлық рационал сандар жиынын екі класка бөлейік, біреуі А болсын, мұны төменгі немесе сол жақтағы класс дейміз; екінішсі В болсын, мұны жоғарғы немесе оқ жақтағы класс дейміз. Бұл А мен В кластары төмендегі шарттарды қанағаттандыруы қажет:
1) әрбір рационал сав А мен В-нің біреуіне ғана жатуы керек: не А -ға, не В -ге;
2) А класына жататын әрбір рационал сан В класына жататын әрбір рационал саннан кем болуы керек. Барлық рационал сандар жиынын осылай етіп екі класқа белуді рационал сандар жиынындағы қима деп атайды.
Бұлай етіп екі класқа бөлу - рационал сандар жиынында тіпті мүмкін нәрсе. Шынында, айталық
 кезкелген рационал сан болсын.
А
класына
кезкелген рационал сан болсын.
А
класына
 -ден кіші барлық рационал сандарды, ал
В
класына
-ден кіші барлық рационал сандарды, ал
В
класына
 -ден үлкен барлық рационал сандарды жатқызайык. Сонда
-ден үлкен барлық рационал сандарды жатқызайык. Сонда
 бүкіл рационал сандардың жиынын, жоғарыда көрсетілген екі шартты толығы мен қанағаттандыратын екі классқа бөледі.
бүкіл рационал сандардың жиынын, жоғарыда көрсетілген екі шартты толығы мен қанағаттандыратын екі классқа бөледі.
 санын өзін не
А
класына, не
В
класыка жаткызуға болады. Егер
санын өзін не
А
класына, не
В
класыка жаткызуға болады. Егер
 -ді
А
-класына жатқызсақ, онда ол
А
класының ішіндегі рационал сандардың ең үлкені болып табылады. Егер
-ді
А
-класына жатқызсақ, онда ол
А
класының ішіндегі рационал сандардың ең үлкені болып табылады. Егер
 -ді
В
класына жатқызайық, онда ол
В
класын құратын рационал сандардың ішіндегі ең кішісі болып табылады.
-ді
В
класына жатқызайық, онда ол
В
класын құратын рационал сандардың ішіндегі ең кішісі болып табылады.
Барлық рационал сандар жиынын осылай етіп екі класка бөлгенде, төменгі
А
класын құрушы сандардың ішінде ең үлкені бар, ол
 ,
онда
В
класын кұратын сандардын ішінде ең кішісі жоқ немесе
В
класын құрушы сандардың ішінде ең кіші сан бар, ол
,
онда
В
класын кұратын сандардын ішінде ең кішісі жоқ немесе
В
класын құрушы сандардың ішінде ең кіші сан бар, ол
 ,
бірақ онда
А
класында ең үлкен сан жоқ.
,
бірақ онда
А
класында ең үлкен сан жоқ.
Тағы да бүкіл рационал сандар жиынын екі класка бөлейік: біреуі А, екіншісі В болсын. Бұрынғыша А- төменгі класс, В - жоғарғы класс. А класына барлық теріс сандарды, нольді және квадратты екіден кем оң рационал сандарды жатқызалық та, В класына квадраты екіден артық он рационал сандарды жатқызалық.
Мысалы, 1, 1 саны А класына жатады, өйткені (1, 1) 2 = = 1, 21<2, ал 1, 6 саны В класына жатады, себебі (1, 6) 2 = = 2, 56>2.
Осылай етіп бүкіл рационал сандар жиыным екі класка бөлуді ол жиындағы екінші типті қима дейді.
Осы қима жөнінде келесі теореманы дәлелдейік.
Теорема. Бұл жолы А жиынын құратын рационал сандардың ішінде ең үлкені жоқ, В жиынын құратын рационал сандардың ішінде ең кішісі жоқ.
А класын құратын рациоиал сандардың ішінде ең үлкен сан бар деп кері ұйғарайық және ол сан а болсын. Архимед аксиомасы бойынша
п (2
-
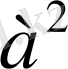 )
> 2
а +
1
)
> 2
а +
1
теңсіздікті қанағаттандыратын үлкен п натурал саны әрқашан да табылады. Бұл теңсіздіктен

теңсіздіті шығады.
Егер кейінгі теңсіздік орындалатын болса, онда мына теңсіздік

сөзсіз орындалады. Бұл арадан
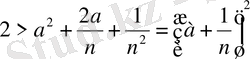
немесе
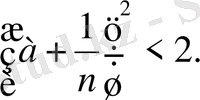
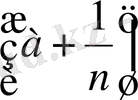 санының квадраты 2-ден аз болғандықтан, бұл сан
А
класына жатады және
а
санынан артық. Олай болса,
А
класын құратын рационал сандардық ішінде ен үлкен сан бар, ол
а
деп теоремаға қарсы ұйғарғанымыз дұрыс болып шықпады. Міне осы қайшылық теоремалық дұрыстығын дәлелдейді.
санының квадраты 2-ден аз болғандықтан, бұл сан
А
класына жатады және
а
санынан артық. Олай болса,
А
класын құратын рационал сандардық ішінде ен үлкен сан бар, ол
а
деп теоремаға қарсы ұйғарғанымыз дұрыс болып шықпады. Міне осы қайшылық теоремалық дұрыстығын дәлелдейді.
Енді теореманың
«В
класын құратын рационал сандардың ішінде ең кішісі жоқ» деген бөлімін дәлелдейік. Ол үшін алғашқыдай кері ұйғарайық:
В
класында ең кіші сан бар және ол
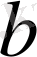 болсын. Тағы да Архимед аксиомасы бойынша
болсын. Тағы да Архимед аксиомасы бойынша
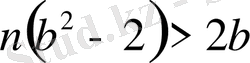 ,
,
немесе
 , олай болса,
, олай болса,
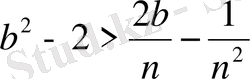
бұл арадан:
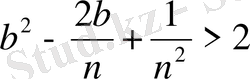 немесе
немесе
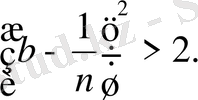
Осы, кейінгі, теңсіздіктен біз мынаны байқаймыз:
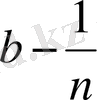 санының квадраты 2-ден артык, ендеше бұл сан
В
класына жатады. Ал
санының квадраты 2-ден артык, ендеше бұл сан
В
класына жатады. Ал
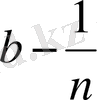 саны
саны
 -ден кем, сондықтак
-ден кем, сондықтак
 саны
В
класында ең кіші сан бола алмайды. Бұл да біздін ұйғаруышыздың дұрыс емес екендігін, теоремалық дұрыстығын көрсетеді.
саны
В
класында ең кіші сан бола алмайды. Бұл да біздін ұйғаруышыздың дұрыс емес екендігін, теоремалық дұрыстығын көрсетеді.
Жоғарыдағы айтылғаңдардан мынадай қортындыға келуге болады.
Егер барлық рационал сандар жиынындағы қиманы алсақ, яғни бүкіл рационал сандарды екі класқа - төменгі класс А -ға және жоғарғы класс В -ге-бөлсек, төменгі кластық әрбір саны жоғарғы кластын, әрбір санынан кем болып келсе, онда мынадай үш жағдай болуға мүмкін:
1) не төменгі
А
класында ең үлкен сан
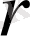 бар, онда жоғарғы класта ең кіші сан болмайды;
бар, онда жоғарғы класта ең кіші сан болмайды;
2) не жоғарғы
В
хлаоында ек ікіші сан
 бар, онда теменгі класта үлкен сан болмайды;
бар, онда теменгі класта үлкен сан болмайды;
3) төменті А класында ек үлікен сан, жоғарғы В класында ең кіші сан болмайды.
Егер 1 және 2-жағдайлар орындалса, онда рационал сандар жиынындағы қима
(А, В)
рационал
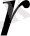 санын анықтайды, яғни бүкіл рационал сандар жиынын жоғарыдағыдай екі класка бөлуші рационал
санын анықтайды, яғни бүкіл рационал сандар жиынын жоғарыдағыдай екі класка бөлуші рационал
 саны болды.
саны болды.
Егер 3-жағдай орындалса, онда қима
(А, В)
бір ғана иррационал санды анықтайды дейміз, яғни бүкіл рационал сандар жиынын жоғарыдағы көрсетілген екі класқа бөлуші рационал-сан болмайды, иррационал сан болады, Біздің мысалга келтірген қима
(А, В)
мына
 символға сәйкес келетін иррационал санды анықтайды. Сонымен, иррационал сан деп қандай санды айтады деген сұрақда былай жауап беруге болады:
иррационал сан деп бүкіл рационал сандар жиынындағы екінші типті қиманы анықтайтын санды айтады.
символға сәйкес келетін иррационал санды анықтайды. Сонымен, иррационал сан деп қандай санды айтады деген сұрақда былай жауап беруге болады:
иррационал сан деп бүкіл рационал сандар жиынындағы екінші типті қиманы анықтайтын санды айтады.
Сонымен, рационал сандардағы олқылықты иррационал сандар енгізіп толтырамыз.
Иррационал сандарды өзара былайша салыстырамыз.
 Егерде рационал сандар жиынындығы екі
(А, В)
және (
Егерде рационал сандар жиынындығы екі
(А, В)
және (
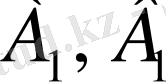 ) қималарының төменгі кластары ортақ сандардан құралса, яғни
А
класының әрбір саны
) қималарының төменгі кластары ортақ сандардан құралса, яғни
А
класының әрбір саны
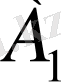 класында жатса және
класында жатса және
 класының әрбір саны
А
класында жатса, бұл екі қиманы бірдей дейміз. Бұл жағдайда осы қималардың анықтайтын сандары
а
мен
класының әрбір саны
А
класында жатса, бұл екі қиманы бірдей дейміз. Бұл жағдайда осы қималардың анықтайтын сандары
а
мен
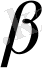 болса, оларды өзара тең (1-чертёж) дейміз де, былай жазамыз:
а
=
болса, оларды өзара тең (1-чертёж) дейміз де, былай жазамыз:
а
=
 .
.
Егер
А
класынын, ішінде
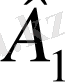 класының сандары да болса,
а
-ны
класының сандары да болса,
а
-ны
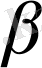 -ден үлкен дейміз де,
а
>
-ден үлкен дейміз де,
а
>
 деп жазамыз.
деп жазамыз.
Егерде а - санын анықтаушы қиманың төменгі класында оң сандар болса, а -ны оң таңбалы сан дейді де, жоғарғы класында теріс сандар болса, а -ні теріс таңбалы сан деп атайды.
Иррационал теңдеулер
Айнымалысы түбір тақбасынын, астында тұратын теңдеу
иррационал теңдеу
деп аталады. Мысалы, мына теңдеу:

1-м ы с а л.
 теңдеуді шешейік.
теңдеуді шешейік.
Бұл теңдеудің екі жақ бөлігін де квадрат дәрежеге шығарамыз, сонда
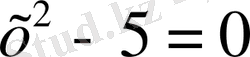 шығады, бұдан
х
2
= 9, яғни
х =
3 не
х =
-3 табылады.
шығады, бұдан
х
2
= 9, яғни
х =
3 не
х =
-3 табылады.
Енді осы табылған сандар теңдеудің шешімдері бола ма, соны тексерейік. Шынында да оларды осы теңдеуге қойсақ, тура теңдіктер шығады:
 және
және
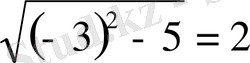
Олай болса,
х-
3 және
 берілген теңдеудің шешімдері.
берілген теңдеудің шешімдері.
2-м ы с а л.
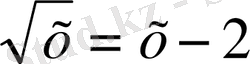 теңдеуін шешейік. Теңдеудің екі жағын да квадрат дәрежеге шығарайық:
теңдеуін шешейік. Теңдеудің екі жағын да квадрат дәрежеге шығарайық:
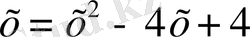 . Ықшамдағаннан кейін мынадай квадрат теңдеу шығады:
. Ықшамдағаннан кейін мынадай квадрат теңдеу шығады:
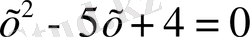 ,
мұның түбірлері:
,
мұның түбірлері:
 және
және
 . Осы табылған сандар берілген теңдеудің шешімдері бола ма, соны тексерейік. 4 санын теңдеуге қойғанда
. Осы табылған сандар берілген теңдеудің шешімдері бола ма, соны тексерейік. 4 санын теңдеуге қойғанда
 тура теңдік шығады, яғни 4 саны - берілген теңдеудің шешімі. Ал 1 санын қойсақ, онда оң жағында-1 саны шығады. Демек, 1 саны теңдеудің шешімі бола алмайды; оны
бөгде түбір
дейді (теңдеуді осы тәсілмен шешу нәтижесінде пайда болған) . Ж а у а б ы:
тура теңдік шығады, яғни 4 саны - берілген теңдеудің шешімі. Ал 1 санын қойсақ, онда оң жағында-1 саны шығады. Демек, 1 саны теңдеудің шешімі бола алмайды; оны
бөгде түбір
дейді (теңдеуді осы тәсілмен шешу нәтижесінде пайда болған) . Ж а у а б ы:
 .
.
Біз иррационал теңдеуді шешкенде табылған шешімдерді тексеру қажет болатынын көріп отырмыз, сондықтан да, мысалы, тура емес теңдікті квадрат дәрежеге шығарғанда тура теңдік шығуы мүмкін. Шынында да, тура емес
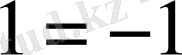 теңдеуін квадрат дәрежеге шығарғанда тура теңдік
теңдеуін квадрат дәрежеге шығарғанда тура теңдік
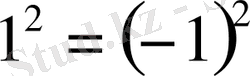 шығады.
шығады.
3-м ы с а л.
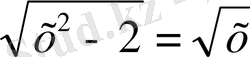 теңдеуін шешейік.
теңдеуін шешейік.
Бұл теңдеудің екі жағын да квадрат дәрежеге шығарайық:
 бұдан мынадай квадрат теңдеу шығады:
бұдан мынадай квадрат теңдеу шығады:
 мұның түбірлері:
мұның түбірлері:
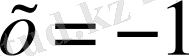 және
х = 2.
Сонда -1 саны бұл теңдеудің түбірі бола алмайтыны бірден-ақ байқалады, өйткені
және
х = 2.
Сонда -1 саны бұл теңдеудің түбірі бола алмайтыны бірден-ақ байқалады, өйткені
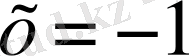 болғанда бұл теңдеудің екі жағы да анықталмайды. Теңдеуге 2 санын қойғанда мынадай тура теңдік шығады:
болғанда бұл теңдеудің екі жағы да анықталмайды. Теңдеуге 2 санын қойғанда мынадай тура теңдік шығады:
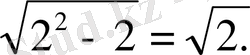 Демек, берілген теңдеудің шешімі тек 2 саны ғана болады.
Демек, берілген теңдеудің шешімі тек 2 саны ғана болады.
4-мысал.
 теңдеуін шешейік. Бұл теңдеудің екі жағын да квадрат дәрежеге шығарып, мынаны табамыз:
теңдеуін шешейік. Бұл теңдеудің екі жағын да квадрат дәрежеге шығарып, мынаны табамыз:
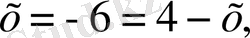
 және
х = 5.
Орнына қоя отырып, 5 саны теңдеудің түбірі бола алмайтынына көз жеткіземіз. Сондықтан теңдеудің шешімдері болмайды.
және
х = 5.
Орнына қоя отырып, 5 саны теңдеудің түбірі бола алмайтынына көз жеткіземіз. Сондықтан теңдеудің шешімдері болмайды.
Кейде иррационал теңдеулерді мәндес ауыстыруларды қолданып шешкен ыңғайлы:
5-м ы с а л.
 теңдеуін шешейік.
теңдеуін шешейік.
Анықтама бойынша
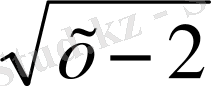 деген - квадраты түбір астындағы ернекке тең болатын теріс емес сан. Басқаша айтқанда,
деген - квадраты түбір астындағы ернекке тең болатын теріс емес сан. Басқаша айтқанда,
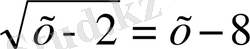 теңдеуі мына жүйемен мәндес
теңдеуі мына жүйемен мәндес

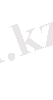
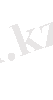

Жүйенің бірінші теңдеуін шешеміз, ол болса,
х
2
- 17х+66= 0
теңдеуімен мәндес, сонда табылатын түбірлер 11 мен 6, алайда мына шарт
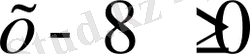 тек
тек
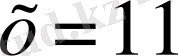 мәнінде ғана орындалады. Сондықтан берілген теңдеудің тек бір ғана түбірі бар:
х=
11.
мәнінде ғана орындалады. Сондықтан берілген теңдеудің тек бір ғана түбірі бар:
х=
11.
6-м ы с а л.
 теңдеуін шешейік.
теңдеуін шешейік.
Алдыңғы шығарылған мысалдардан мұның өзгешелігі сол, бұл иррационал теңдеуге квадрат түбір емес, үшінші дәрежелі түбір енген. Сондықтан радикалдан арылу үшін теңдеудін, екі белігін да екінші дәрежеге емес, үшінші дәрежеге шығару керек:
( х - 1) 3 = х 2 - х- 1 . Түрлендіргеннен кейін табылатыны:
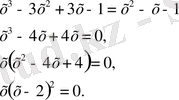
Сонымен,

7-м ы с а л. Мынадай теңдеулер жүйесін шешейік:

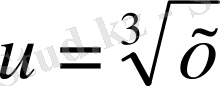 және
және
 деп алып, келесі жүйеге келеміз:
деп алып, келесі жүйеге келеміз:
Екінші теңдеудің сол жақ бөлігін көбейткіштерге жіктейік:
 содан кейін бүған бірінші теңдеуден
содан кейін бүған бірінші теңдеуден
 мәнін қоямыз. Сонда екіншімен мәндес мына жүйе шығады:
мәнін қоямыз. Сонда екіншімен мәндес мына жүйе шығады:

Бірінші теңдеуден табылған
 мәнін
мәнін
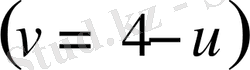 екінші теңдеуге қойып, мынадай теңдеуге келеміз:
екінші теңдеуге қойып, мынадай теңдеуге келеміз:
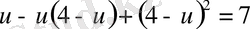 , яғни
, яғни
 .
.
Осы табылған квадрат теңдеудің екі түбірі бар:
 және
және
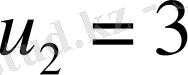 .
.
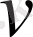 -нің сәйкес мәндері мынадай:
-нің сәйкес мәндері мынадай:
 және
және
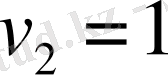 . Енді
х
пен
у
айнылалыларына ауыссақ, мынаны табамыз:
. Енді
х
пен
у
айнылалыларына ауыссақ, мынаны табамыз:
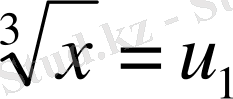 яғни
яғни
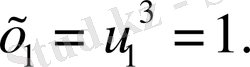
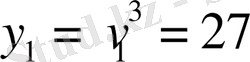 ,
,
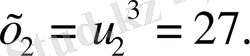
 Жауабы: (. 1; 27), (27; 1) .
Жауабы: (. 1; 27), (27; 1) .
ИРРАЦИОНАЛ ТЕҢДЕУЛЕР
Иррационал теңдеулерді шешкенде иррационалдықтардан құтылу әдістері қолданылады. Сондықтан тапқан түбірлерді тексеру қажет. Әдетте бөтен түбірлер берілген тендеудің екі жағын жұп дәрежеге шығарғанда немесе "көбейтінді нөлге тең болу үшін ең болмағанда бір көбейткіш нөлге тең болу керек" - деген ережені мұқият қолданбағанда пайда болады. Негізгі типтік есептерді шығару мысалдарын қарастыралық.
1. Тендеуді шешіңдер:

Ш е ш у і. Иррационалдықтан құтылу үшін екі жағын квадраттаймыз:
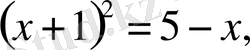

 ,
,

- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz