Гравитациялаушы және кедергілі ортадағы массасы, өлшемі және пішіні айнымалы бейстационар үш ості эллипсоид өрісіндегі материялық нүктенің қозғалысы


ӘОЖ 521. 1 қолжазба құқығында
БАЙДОЛДА ФАРИДА
Гравитациялаушы және кедергілі ортадағы бейстационар үш ості эллипсоид тартылыс өрісіндегі материялық нүктенің қозғалысы
01. 03. 01 - астрометрия және аспан механикасы
мамандығы бойынша физика-математика ғылымдарының кандидаты
ғылыми дәрежесін алу үшін ұсынылған диссертациясының
Авторефераты
Қазақстан Республикасы
Алматы, 2010
Жұмыс «Ұлттық Ғарыштық Зерттеулер мен Технологиялар Орталығы» акционерлік қоғамының «В. Г. Фесенков атындағы Астрофизикалық институты» еншілес жаупкершілігі шектеулі серіктестігінде орындалды
Ғылыми жетекшісі: физика-математика ғылымдарының
докторы М. Ж. МИНГЛИБАЕВ
Ресми оппоненттер: физика-математика ғылымдарының докторы Қ. А. Омарқұлов
физика-математика ғылымдарының
кандидаты Қ. С. Жилисбаева
Жетекші ұйым: Абай атындағы Қазақ Ұлттық
Педагогикалық Университеті
Қорғау 2010 жылы « 25 »-ші қазан сағат 15 00 - де « Ұлттық Ғарыштық Зерттеулер мен Технологиялар Орталығы » акционерлік қоғамы жанындағы БД 53. 03. 01 Біріккен диссертациялық кеңесінің мәжілісінде өтеді.
Мекен-жайы: 050010, Алматы қ., Шевченко к-сі, 15, Кіші конференц залы.
Диссертациямен «В. Г. Фесенков атындағы Астрофизикалық институты» ЕЖШС кітапханасында немесе www. spaceres. kz сайтынан танысуға болады.
Мекен-жайы: 050020, Алматы қ., Каменское плато, Обсерватория, 23, телефон: (727) 260-75-90, Е-mail: nkit@spaceres. kz
Автореферат 2010 жылы «» қыркүйекте таратылды
Диссертациялық кеңестің ғылыми
хатшысы, физика-математика
ғылымдарының докторы, профессор Э. Я. Вильковиский
КІРІСПЕ
Жұмыстың жалпы сипаттамасы . Гравитациялаушы дененің массасы мен өлшемінің өзгеру салдары бейстационар нақты ғарыштық жүйе динамикалық эволюциясының негізгі факторларының бірі болып табылады. Осы жұмыста массасы, өлшемі және пішіні айнымалы еркін екі дене мәселесі шектелген қойылымда қарастырылып, оның интегралданатын жағдайлары табылған және оларға талдау жасалған.
Бейстационар гравитациялаушы аспан денелерінің қозғалысын зерттеуде алынған бірқатар маңызды нәтижелер Қазақстан Республикасы Ұлттық Ғылыми Академиясының академигі Т. Б. Омаровтың және оның ғылыми мектебінің түлектері Т. С. Кожановтың, А. А. Бековтың, Қ. С. Омарқұловтың, Е. А. Малковтың және М. Ж. Минглибаевтің докторлық диссертацияларында келтірілген. Бейстационар эллипсоид өрісіндегі дене қозғалысының әртүрлі динамикалық моделін құрып, оларды ауқымды түрде зерттеген Romain G., Pierre B. және А. А. Бековтың жұмыстарын ерекше атап өтуге болады.
Зерттеу жұмысының өзектілігі. Қазіргі кездегі астрономиялық бақылаулар ғарыштық объектілердің массалары, өлшемдері және пішіндері уақытқа тәуелді айнымалы болатындығын көрсетіп отыр. Аталған айнымалы параметрлердің динамикалық салдарын зерттеу бейстационар гравитациялаушы жүйелердің ерекше эволюциялық сипаттамаларын ашып береді. Бейстационар құрылымды гравитациялық жүйе эволюциясын зерттеу ғаламдағы ірі өлшемді құрылымдар мен құбылыстардың динамикалық табиғатын түсінуге мүмкіндік береді. Сондықтан да сәйкес моделдер негізінде әр түрлі тәсілдерді пайдаланып бейстационар аспан денелерінің қозғалысын аналитикалық зерттеу - бүгінгі күндегі аспан механикасының өзекті мәселелердің бірі болып табылады.
Жұмыстың мақсаты. Диссертациялық жұмыста гравитациялаушы және кедергілі ортадағы массасы, пішіні мен өлшемі айнымалы, дербес жағдайда өлшемі тербелмелі, үш ості дененің тартылыс өрісіндегі материялық нүктенің қозғалысын қарастырып оның динамикалық эволюциясын зерттеу негізгі мақсат болып табылады.
Зерттелетін мәселелер. Гравитациялаушы және кедергілі ортадағы екі және үш ості дененің үш сипаты - массасы, пішіні мен өлшемі айнымалы болғандағы оның ньютондық өрісіндегі нүкте қозғалысын зерттеуде туындайтын мәселелер.
Зерттеу нысаны. Гравитациялаушы және кедергілі ортадағы массасы, өлшемі және пішіні айнымалы екі және үш ості эллипсоид өрісіндегі материялық нүкте қозғалысы.
Зерттеу әдістері . Квазиконустық қима бойынша апериодтық қозғалыс негізіндегі ұйытқу теориясы кеңінен пайдаланылады. Қозғалыс теңдеуі әртүрлі жүйедегі ұйытқыған лездік элементтер арқылы қарастырылады. Осы жұмыста канондық ұйытқу теориясы, динамикалық жүйенің фазалық кеңістіктегі зерттеу тәсілдері және эллиптикалық функциялар теориясы пайдаланылған. Сонымен қатар Maple, Mathlab және тағы басқа математикалық программалардың аясында графиктерді алу тәсілдері қолданылған.
Жұмыстың ғылыми жаңалығы. Диссертациядағы мына нәтижелер жұмыстың ғылыми жаңалығы болып табылады :
- гравитациялаушы және кедергілі ортадағы бейстационар -айнымалы екі өлшемді эллипсоид өрісіндегі нүктенің әртүрлі ұйытқыған дифференциалдық қозғалыс теңдеулер жүйесінің жеті интегралданатын жағдайы анықталды;
- гравитациялаушы және кедергілі ортадағыайнымалы екі өлшемді эллипсоид өрісіндегі материялық нүктенің канондық қозғалыс теңдеуінің екі жағдайы үшін шешімі алынды;
- гравитациялаушы және кедергілі ортадағыайнымалы үш өлшемді эллипсоид өрісіндегі материялық нүктенің әртүрлі дифференциалдық қозғалыс теңдеулерінің екі интегралданатын жағдайы және орбита жазықтығының фазалық портреті анықталып, орнықтылық аймағы көрсетілді;
- эллипсоидтың , тербелмелі өлшемі мен оның өрісіндегі нүкте қозғалысының арасындағы резонанс жағдайындағы дифференциалдық теңдеулер алынып, табылған теңдеулер жүйесінің интегралданатын жағдайы анықталды.
Қорғауға шығарылатын тұжырымдар. Диссертациядағы зерттеулердің нәтижелері ретінде қорғауға мына тұжырымдар ұсынылады:
- массасы мен өлшемі кез келген заңдылықпен өзгеретін, ал пішінінің сипаты ретінде- екінші зоналдық гармоникасы айнымалы деп қарастырылып, осы жағдайда әртүрлі дифференциалдық қозғалыс теңдеулер жүйесіндегі жаңа жеті қатаң дербес және бір жуық жалпы шешімі және оларды талдау;
- массалары мен өлшемі әртүрлі қалыпта айнымалы, ал орталық дененің пішіні ретіндеайнымалы деп қарастырып, материялық нүктенің канондық қозғалыс теңдеуінің интегралданатын екі жағдайының қатаң дербес шешімі анықталып талданады;
- массасы мен өлшемі кез келген заңдылықпен өзгеретін, ал пішінінің сипаты ретіндеайнымалы деп қарастырып дифференциалдық қозғалыс теңдеулерінің екі интегралданатын жуық жалпы жағдайы табылып талданды;
- массасы мен өлшемі айнымалы, ал пішініайнымалы дененің орнықтылық және орнықсыздық аймағыныңжазықтығында фазалық портретінің құрылуы, қозғалыс сипатының тек дененің бас инерция моменттеріне тәуелді болатындығы көрсетілген;
- гравитациялаушы және кедергілі бейстационар екі өсті эллипсоидтың өрісіндегі нүкте қозғалысының резонанстық жағдайында Делоне аномалиясы енгізіліп алынған қозғалыс теңдеуі және оның жуық жалпы шешімідері.
Зерттеу нәтижелерінің дұрыстығы. Диссертацияда қарастырылған мәселелерді зерттеуде ұйытқыған қозғалыстың әртүрлі теңдеулері және ұйытқу теориясының белгілі тәсілдері пайдаланылған. Сонымен қатар, канондық ұйытқу теориясының математикалық аппараты кеңінен сәтті қолданылған. Динамикалық жүйенің фазалық кеңістіктегі қасиеттерін зерттеудегі белгілі тәсілдері пайдаланылған. Диссертацияда алынған теңдеулердің шешімдері массасы, өлшемі және пішіні тұрақты жағдайларда басқа авторлардың нәтижелерімен дәл сәйкес келеді. Жоғарыда айтылғандар зерттеу нәтижелерінің дұрыстығын көрсетеді.
Жұмыс нәтижелерінің теориялық және іс жүзіндегі маңыздылығы. Диссертацияда табылған жаңа шешімдерді аспан механикасында кездесетін күрделі мәселелерді зерттеуде алғашқы жуық қозғалыс ретінде қабылдауға болады. Алынған нәтижелер ғарыштанудағы бейстационар жүйелерді зерттеудің кезектегі сатысы болып, әрі қарай ғаламдағы күрделі бейстационар құбылыстарды зерттеуге жаңа мәселелердің қойылымын нақтылайды. Ал, ғылыми іс жүзіндегі маңызы - табылған жаңа шешімдерді аспан денелерінің жасанды және табиғи серігінің динамикалық эволюциясының моделін құрып есептеуде пайдалануға болады.
Жұмыстың басқа ғылыми - зерттеу жұмыстарымен байланысы.
Диссертациядағы ғылыми - зерттеу жұмыстары сәйкес жоспарымен Қазақстан Республикасының білім және ғылым министерлігінің мынадай іргелі зерттеулерінің бағдарламалары бойынша жүргізілді:
- «Зерттеулердің ғылыми-әдістемелік негізін дамыту және ғарыштық кеңістікті пайдалану, Жерді ғарыштан зерттеуді Қазақстан Республикасының әлеуметтік-экономикалық және технологиялық мақсаттарында дамыту» - іргелі зерттеулер бағдарламасы, шифр Ф. 0351, «Ғаламдық жүйелердегі астрономиялық зерттеулер, жұлдыз және планета» - түп бағдарламасы бойынша, шифр Ф. 0351 - 1. Іске асыру мерзімі 2006 - 2008 жж. «Ғарыштық күшті өрістердегі табиғи және жасанды аспан денелерінің динамикасын зерттеу» - жобасы. Мемлекеттік тіркеу № 0106РК00081;
- «Ғаламдық жүйелердегі астрономиялық зерттеулер, жұлдыз және планета» - іргелі зерттеулердің бағдарламасы, шифр Ф. 0487. Іске асыру мерзімі 2009-2010 жж. «Әлемді гравитациялаушы жүйелердің динамикасы мен құрылымын зерттеу» - жобасы бойынша, мемлекеттік тіркеу № 0109РК00284.
Жұмыстың аппробациясы. Жұмыстың негізгі нәтижелері мына конференцияларда баяндалды: Екінші Фесенковтық оқулар - «Қазіргі астрофизика: дәстүрлері мен болашағы» атты халықаралық ғылыми конференциясы (Алматы, 2007) ; Халықаралық жас ғалымлар, магистранттар мен студенттердің «Ғылым әлемі» конгресі (Алматы, 2007) ; «Қазіргі Қазақстанға инновациялық даму мен ғылымның қажеттігі» -Республикалық ғылыми-практикалық конференциясы (Алматы, 2007) ; «Қазіргі уақыттағы физика жетістіктері мен іргелі физикалық білім» - Бесінші халықаралық ғылыми конференциясы (Алматы, 2007) ; «Қазіргі уақыттағы физика жетістіктері мен іргелі физикалық білім» - Алтыншы халықаралық ғылыми конференциясы (Алматы, 2009) ; «Математика, информатика, механика және басқару теориясының өзекті мәселелері» атты халықаралық ғылыми-практикалық конференциясы (Алматы, 2009) ; «Механика және траспорттық қондырғы құрылысы» атты халықаралық ғылыми - практикалық конференциясы (Алматы, 2010) .
Автордың қосқан үлесі. Зерттеу нәтижелері 9 жұмыста жарияланған. Оның ішінде 2, 4 - 5, 7 - 9 жұмыстарда негізгі идея бойынша мәселенің қойылуы ғылыми жетекші де, ал жұмысты орындағын диссертант. Ал, 1, 3, 6 жұмыстарды диссертант өз бетінше орындады. Ал талдау ғылыми жетекшімен бірге орындалды.
Жұмыстың жариялануы. Диссертациялық жұмыс бойынша 9 ғылыми жұмыс, соның ішінде, ҚР БҒМ білім және ғылым саласындағы бақылау Комитеті ұсынған әр түрлі басылымдарда 3 ғылыми мақала жарияланған.
Диссертацияның көлемі және құрылымы. Диссертация мазмұны, кіріспе, үш тараудан тұратын негізгі бөлім, қорытынды, 140 атауы бар қолданылған әдебиеттер тізімі және қосымшадан тұрады. Оның толық көлемі 100 бет, оның ішінде 4 кесте, 30 сурет және 3 қосымша бар.
Автор жұмысты орындау мен жазу барысында үнемі көңіл бөлгені және құнды кеңестер бергені үшін ғылыми жетекшісі физика-математика ғылымдарының докторы М. Ж. Минглибаевқа үлкен алғысын білдіреді. Сонымен қатар автор В. Г. Фесенков атындағы Астрофизикалық институтының ұжымына ғылыми жұмысқа бейімдегені үшін, соның ішінде институттың аға ғылыми қызметкері Б. И. Демченкоға эллиптикалық функциялар теориясы бойынша пайдалы кеңестері мен сынпікірлері үшін алғысын білдіреді.
НЕГІЗГІ БӨЛІМ
Кіріспеде зерттеліп отырған тақырыптың көкейтестілігі негізделеді, жұмыстың мақсаты, ғылыми жаңалығы, оның іс жүзіндегі маңыздылығы және қорғауға шығарылатын нәтижелер тұжырымдалды. Жұмыста қарастырылатын мәселелерге арналған әдебиетке қысқаша шолу жасалды.
Бірінші бөлімде аспан денелерінің тартылыс өрісіндегі нүктенің қозғалысын зерттеудегі ыңғайлы модель - ол денені үш ості эллипсоид (біртекті, не біртекті емес) деп қарастырылған.
- -ші пунктте массасы, өлшемі және пішіні айнымалы дененің инерция эллипсоиды сипаттамалары, бас инерция моменттерінің қасиеттері қарастырылып, қажетті мәліметтер келтірілген.
- -ші пунктте массасы мен өлшемі айнымалы үш ості дененің гравитациялық өрісі қарастырылып, орталық дененің бас инерция моменттері мен өлшемінің сипаты ретінде алынатын гармоникалар қарастырылып, зерттелетін мәселелерге қойылатын шарттар анықталынған.
Диссертацияда қарастырылған мәселелерде орталық дене потенциалы келесі жуық өрнекпен сипатталады
 (1)
(1)
Центрлік дене бейстационар, сондықтанда, бұл жағдайда дене пішіні мен құрылымының беріліуіне байланысты төмендегі үш түрлі жуықтауда мәселелер жеке зерттелінген
(2)
(3)
(4)
- -ші пунктте мәселенің қойылуы мен декарттық координаталар жүйесіндегі қозғалыс теңдеуі қарастырылған. Гравитациялаушы және қарсыласатын ортадағы, массасы мен өлшемі айнымалыдененің гравитация өрісіндегі нүкте қозғалысын қарастырылған. тік бұрышты координаталар жүйесінің бас нүктесіндененің барицентіріне орналастырамыз, ал координата остерін дененің центрлік бас инерциялық остері бойынша бағыттаймыз. Сонымен қатар дененің инерция остерінің бағытын қарастырылған координаталар жүйесінде тұрақты деп аламыз. Сонда материялық нүктенің қозғалыс теңдеуі келесі түрде болады


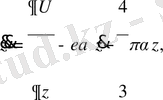 (5)
(5)
мұндағы
 - дененің потенциалы,
- дененің потенциалы,
 - біртекті орта тығыздығы,
- біртекті орта тығыздығы,
 - пропорционалдық коэффициент,
- пропорционалдық коэффициент,
 .
.
- -ші пунктте квазиконустық қима бойынша апериодикалық қозғалыс негізіндегі ұйтқу теориясынан әрі қарай пайдаланылатын қажетті қозғалыс теңдеулері келтірілген.
- -ші пунктте диссертацияда қарастырылған мәселенің дербес жағдайы, центрдегі дене сфера (бір өлшемді эллипсоид) немесе материялық нүкте болған жағдайдағы, лездік элементтердегі қозғалыс теңдеуі анықталған және олардың бірінші ретті толық ғасырлық шешімі табылған.
Екінші бөлімде гравитациялаушы және кедергілі ортадағы бейстационар сфералы емес екі өлшемді дене өрісіндегі нүктенің қозғалысы қарастырылған, оның 6 қатаң дербес және бір жуық жалпы аналитикалық шешімі табылған.
- -ші пунктте бөлімде массасы, өлшеміжәне пішінінің сипаты ретіндеайнымалы зональдық гармониканы ескере гравитациялаушы және кедергілі ортадағы дененің тартылыс өрісіндегі материялық нүктенің қозғалысы зертелген. Материялық нүктенің қозғалысын сипаттайтын бейавтономдық канондық теңдеулер жүйесінің төмендегі қатаң дербес шешімдері табылған
 (6)
(6)
мұндағы
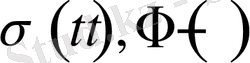 бейстационар дененің сипаттамалары,
бейстационар дененің сипаттамалары,
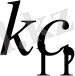 -интегралдау тұрақтысылары.
-интегралдау тұрақтысылары.
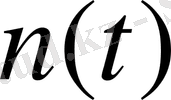 -
-
 осін айнала қозғалатын орбиталдық қозғалыстың бұрыштық жылдамдығы
осін айнала қозғалатын орбиталдық қозғалыстың бұрыштық жылдамдығы
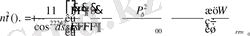
Ал (6) - ші теңдеулердегі
 келесі эллиптикалық квадратурамен анықталады
келесі эллиптикалық квадратурамен анықталады
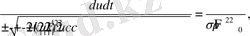
- -ші пунктте эллиптикалық квадратураның дененің бастапқы параметрлеріне байланысты 6 аналитикалық түрі есептелінген. Эллиптикалық интегралды келесі түрде жазамыз
(7)
мұндағы
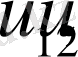 - сәйкес теңдеудің түбірлері. Мәселенің қойылуы бойынша орталық эллипсоидты сығылған
- сәйкес теңдеудің түбірлері. Мәселенің қойылуы бойынша орталық эллипсоидты сығылған
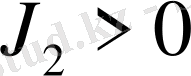 және созылған
және созылған
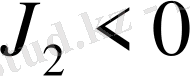 деп қарастырып, (7) - эллиптикалық биквадрат теңдеуді екі жағдай үшін шешеміз. Төмендегі кестеде (7) - ші интегралдың
деп қарастырып, (7) - эллиптикалық биквадрат теңдеуді екі жағдай үшін шешеміз. Төмендегі кестеде (7) - ші интегралдың
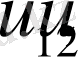 - мәндеріне яғни дененің бастапқы параметрлеріне байланысты бірінші жағдайда төрт шешім, екінше жағдайда екі шешім табылған. Мысалы 1-ші кестеде келтірілген шешімдердің 1/1 - ші жағдайы үшін (6) - ші теңдеулер жүйесіндегі
- мәндеріне яғни дененің бастапқы параметрлеріне байланысты бірінші жағдайда төрт шешім, екінше жағдайда екі шешім табылған. Мысалы 1-ші кестеде келтірілген шешімдердің 1/1 - ші жағдайы үшін (6) - ші теңдеулер жүйесіндегі
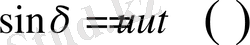 мына өрнекпен анықталады
мына өрнекпен анықталады
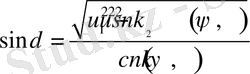 (8)
(8)
Алынған аналитикалық шешімдерді пайдаланып тік бұрышты координаталар жүйесіндегі қозғалыс графикалық түрде төмендегі суреттерде көрсетілген

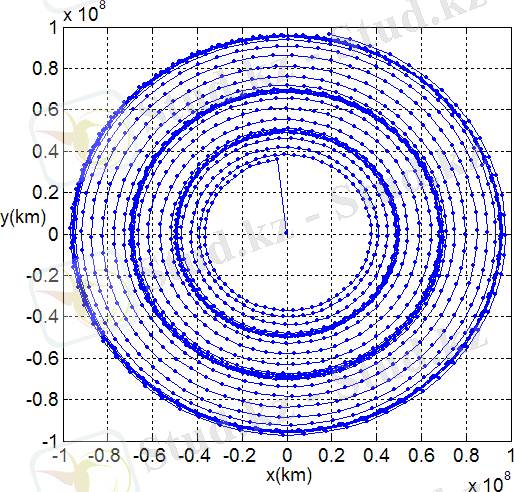
Сурет 1 - Жер сияқты масса центріне қатысты дененің өрісіндегі материялық нүктенің кеңістіктік траекториясы
1-ші кесте
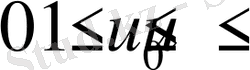
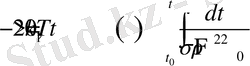

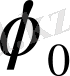
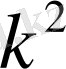
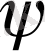

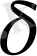
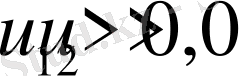
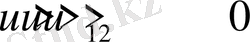
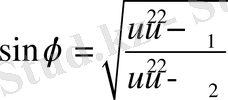
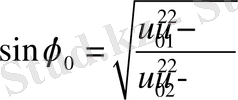
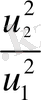
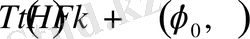
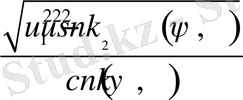
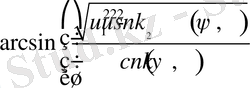
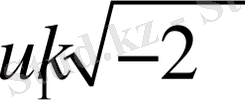
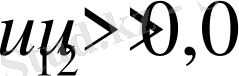
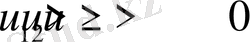
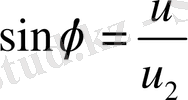
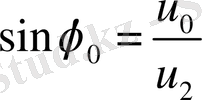
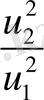
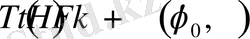
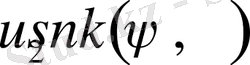
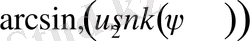
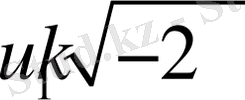

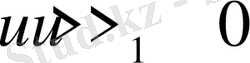
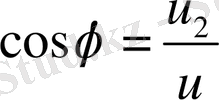
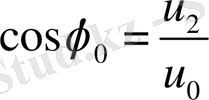
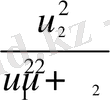
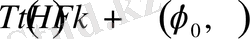
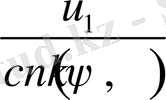
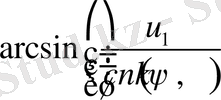
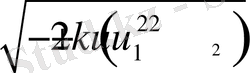
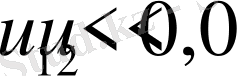
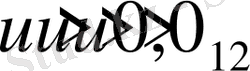
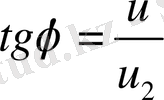
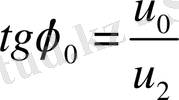
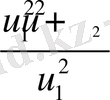
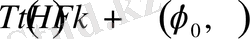
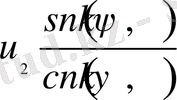
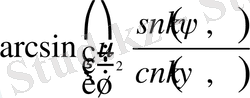
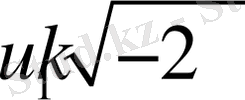
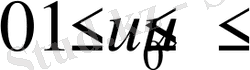
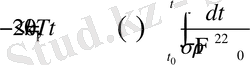

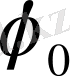
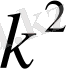
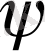

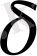
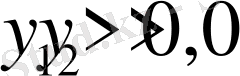
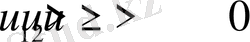
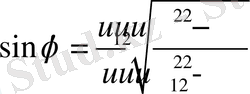
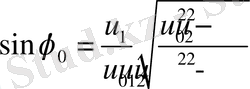
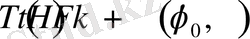
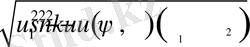
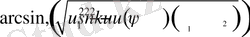
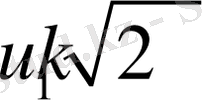
2.

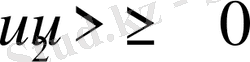
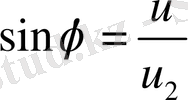
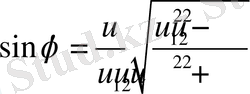
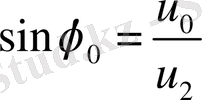
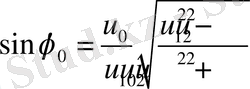
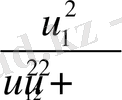
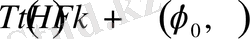
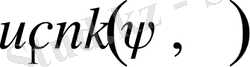
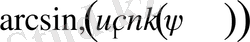
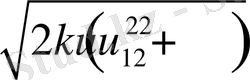
Материялық нүкте көрсетілген суретке сәйкес дененің симметрия осі -
 осі бойымен жоғары көтерілетін ішке қарай жинақталатын спираль бойымен қозғалады. Әрі қарай белгілі бір биіктікке көтерілгеннен кейін керісінше төмен қарай ішке жинақталатын спираль бойымен центрдегі денеге құлайды.
осі бойымен жоғары көтерілетін ішке қарай жинақталатын спираль бойымен қозғалады. Әрі қарай белгілі бір биіктікке көтерілгеннен кейін керісінше төмен қарай ішке жинақталатын спираль бойымен центрдегі денеге құлайды.
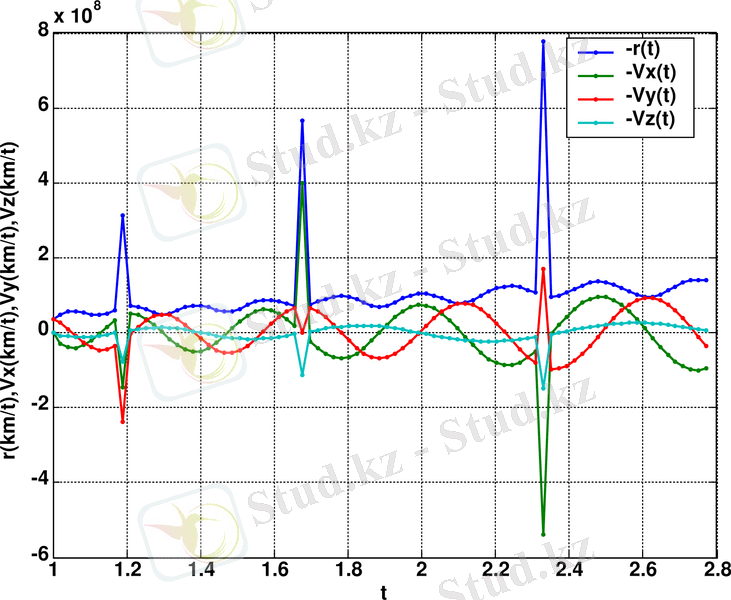
Сурет 2 - Материялық нүкте радиус-вектор модулі мен жылдамдығының проекциялары (
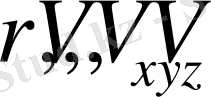 )
)
- -ші пунктте қозғалыс теңдеуінің жуық жалпы шешімі табылған. Тікбұрышты координатажүйесіндегі материялық нүктенің (5) - шi ұйтқыған қозғалыс теңдеуін қарастырамыз
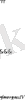 (9)
(9)
 , (10)
, (10)
 . (11)
. (11)
Ұйтқыған ғасырлық қозғалыстың Лагранж теңдеулері келесі түрге келеді
 (12)
(12)
 . (13)
. (13)
Соңғы теңдеулер жүйесінің бірінші ретті толық ғасырлық ұйтқуы табылған.
Сонымен қарастырылған мәселенің табылған қатаң дербес шешімі (8) - ші теңдеу сияқты өрнектермен, ал жуық жалпы шешімдері - бірінші ретті ғасырлық ұйтқу (13) - ші жүйеден анықталады.
- -ші пунктте гравитациялаушы және кедергілі ортадағы массасы, өлшемі жәнезональдық гармоникалары айнымалы бейстационар сфералы емес екі өлшемді эллипсоид өрісіндегі нүктенің канондық дифференциялдық теңдеуінің шешімі алынған
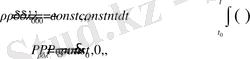 (14)
(14)
мұндағы
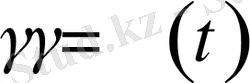 - (11) -ші теңдеумен анықталады,
- (11) -ші теңдеумен анықталады,
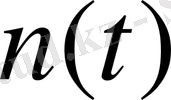 - орбиталдық қозғалыстың бұрыштық жылдамдығы келесі түрде өрнектеледі
- орбиталдық қозғалыстың бұрыштық жылдамдығы келесі түрде өрнектеледі
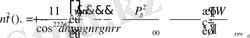
(15)
мұндағы
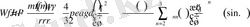
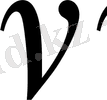 төмендегі квадрат теңдеудің түбірі ретінде анықталады
төмендегі квадрат теңдеудің түбірі ретінде анықталады
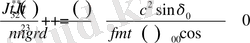 ,
,
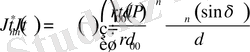 (16)
(16)
- -ші пунктте гравитациялаушы және кедергілі ортадағы нүктенің үш ості массасы, өлшемі және сәйкесгармоникалары айнымалы бейстационар эллипсоид өрісіндегі қозғалысы төмендегіше жазылады



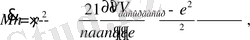 (17)
(17)
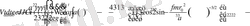 (18)
(18)
Денені сипаттайтын бейстационар эллипсоидтың параметрлеріне қатысты екі жағдайда (17) - ші теңдеулер жүйесі интегралданады. Бірінші жағдайда мына
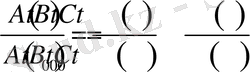 (19)
(19)
шарттар орындалсын немесе
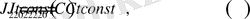 , мұндағы
, мұндағы
 бейстационар эллипсоидтың екінші ретті инерция моменттері. Екінші жағдайда
бейстационар эллипсоидтың екінші ретті инерция моменттері. Екінші жағдайда
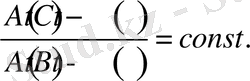 (20)
(20)
(19) -ші немесе (20) -ші шарттары орындалғанда (17) -ші теңдеу жүйесінен мына интеграл табылған
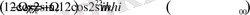
 (21)
(21)
Эллипсоид сығылған дене (Жер сияқты) деп қарастырамыз. Бұл жағдайда
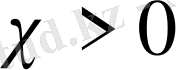 .
.
Келтірілген (17) - ші теңдеулер жүйесінен (21) - ші интегралды ескере мына теңдеуді аламыз
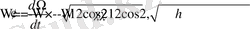 ,
,
 (22)
(22)
(22) - ші теңдеуден
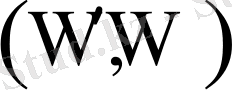 фазалық жазықтығында қозғалыс сипатын анықтайық. Бұл жағдайда мысал ретінде центрдегі дене Жер сияқты деп
фазалық жазықтығында қозғалыс сипатын анықтайық. Бұл жағдайда мысал ретінде центрдегі дене Жер сияқты деп
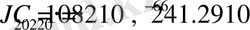 мәндерін қабылдаймыз. Ал материялық нүкте үшін
мәндерін қабылдаймыз. Ал материялық нүкте үшін
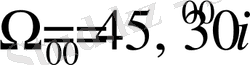 деп қабылдаймыз (Айдың орбиталдық элементтері сияқты) . Төменде
деп қабылдаймыз (Айдың орбиталдық элементтері сияқты) . Төменде
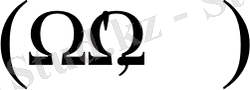 - фазалық жазықтығындағы қозғалыс суреті көрсетілген.
- фазалық жазықтығындағы қозғалыс суреті көрсетілген.
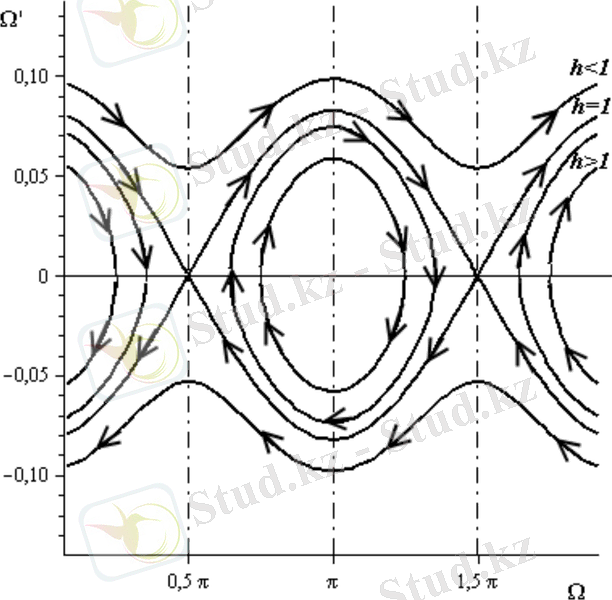
Сурерт 3 -
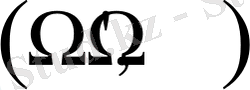 - фазалық жазықтығындағы қозғалыс
- фазалық жазықтығындағы қозғалыс
(22) - ші эллиптикалық интегралды келесі түрде жазайық
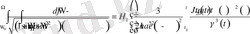 , (23)
, (23)
мұндағы
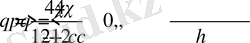
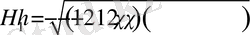 .
.
Алынған (23) - ші интегралды мына түрде жазамыз
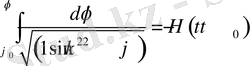 ,
,
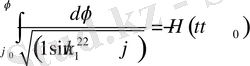 (24)
(24)
мұндағы
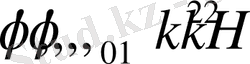 - шамалары
- шамалары
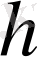 мәніне байланысты төмендегі 2 - ші кестеден анықталады:
мәніне байланысты төмендегі 2 - ші кестеден анықталады:
2 - ші кесте

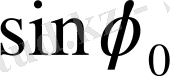
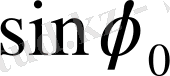
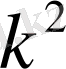
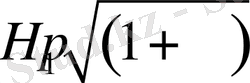
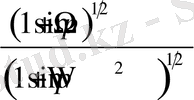
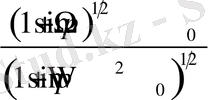
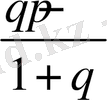

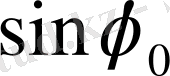
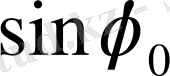
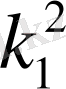
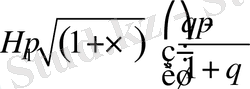
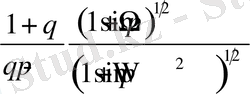
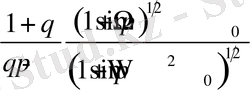
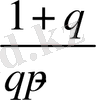
Келтірілген кестедегі түрлендірулердің әр жағдайында интеграл есептелінген.
- . Қозғалыс- шамасы бойынша периодты болады. Сонымен қатаршектеусіз өсе береді.
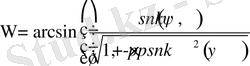 ,
,
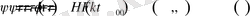 (25)
(25)
- немесе. Қозғалыс- шамасы бойынша ротациялы, сондықтанда қозғалыс шектеулі болады.
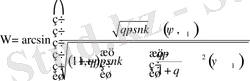 ,
,
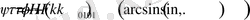 (26)
(26)
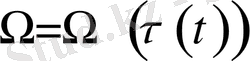 табылғыннан соң,
табылғыннан соң,
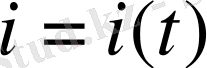 - (21) - ші интегралдан табылады, ал
- (21) - ші интегралдан табылады, ал
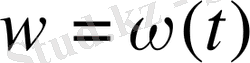 және
және
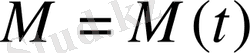 төмендегі өрнектермен анықталады
төмендегі өрнектермен анықталады
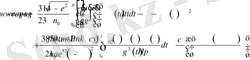 (27)
(27)
мұндағы
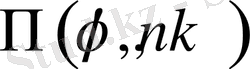 - үшінші текті эллиптикалық интеграл,
- үшінші текті эллиптикалық интеграл,
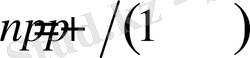 - үшінші текті эллиптикалық интегралдың параметрі,
- үшінші текті эллиптикалық интегралдың параметрі,
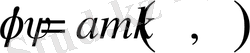 .
.
 (28)
(28)
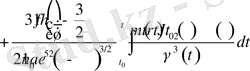
- -ші пунктте (21) - ші интеграл мына түрде жазылған және фазалық кеңістікте оның сапалық сипаттамалары көрсетілген
 (29)
(29)
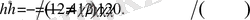 (30)
(30)
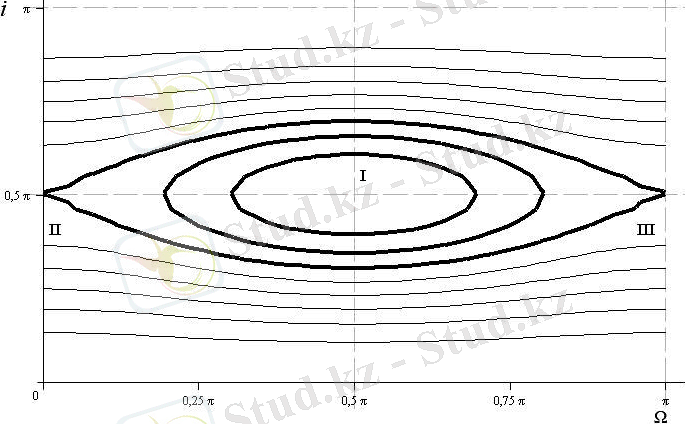
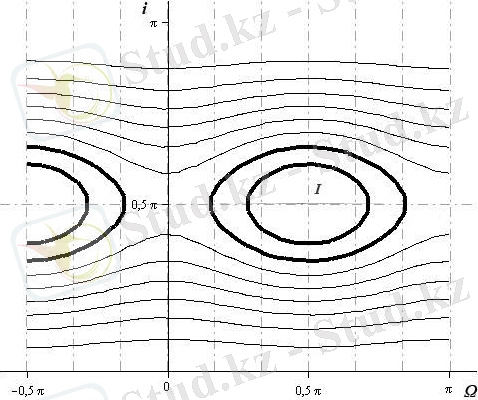
Сурет 5 - Орбита жазықтығының
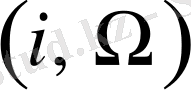 ғасырлық эволюциясы
ғасырлық эволюциясы
Үшінші бөлімде
массасы мен пішіні айнымалы, өлшемі тербелмелі бейстационар эллипсоидтың өрісіндегі нүкте қозғалысының резонанстық жағдайы зерттелген. Есептің қойылу барысы бойынша мұнда резонанс құбылысына сәйкес
 - Делоне аномалиясын келесі түрде енгіземіз:
- Делоне аномалиясын келесі түрде енгіземіз:
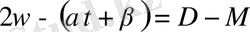 . (31)
. (31)
(31) - ші теңдікті ескере ұйтқушы функцияны келесі түрде жазамыз
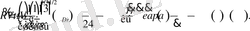 ,
,
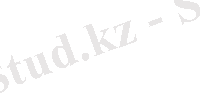 (32)
(32)
ұйтқыушы функцияның
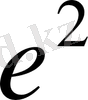 дәлдігімен алынған толық ғасырлық бөлігі келесі теңдеумен анықталады
дәлдігімен алынған толық ғасырлық бөлігі келесі теңдеумен анықталады
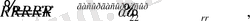 (33)
(33)
мұндағы
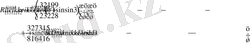
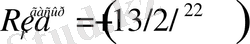 ,
,
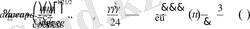
Делоне аномалиясы енгізілген лездік элементтеріндегі табылған қозғалыс теңдеуі келесі түрде жазылады
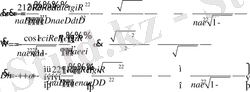 (34)
(34)
Ғасырлық қозғалыс теңдеулерінің интегралданатын жағдайлары.
Ұйтқыған (34) - ші теңдеулерден мына интегралдарды аламыз:
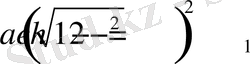 ,
,
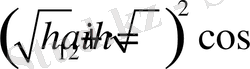 (35)
(35)
Әрі қарай
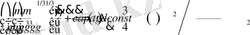
деп қабылдасақ (34) - ші теңдеулер жүйесінен төмендегі интегралды аламыз
 . (36)
. (36)
Аталмыш (35) - ші және (36) - ші интегралдарын пайдаланып, (34) - ші теңдеулер жүйесінің шешімі квадратураға келтіріледі.
Қорытынды
Жасалған зерттеулердің негізгі нәтижелерін келесі түрде тұжырымдауға болады:
- гравитациялаушы және кедергілі ортадағы массасы мен өлшемі кез келген заңдылықпен өзгеретін, ал пішінінің сипаты ретінде екінші зоналдық гармоникасы айнымалы бейстационар екі өлшемді дененің тартылыс өрісіндегі материялық нүктенің ғасырлық қозғалысын қарастырып, әртүрлі дифференциалдық қозғалыс теңдеулер жүйесіндегі алты қатаң дербес және бір жуық жалпы шешімі табылған;
- гравитациялаушы және кедергілі ортадағы массалары мен өлшемі әртүрлі қалыпта айнымалы, ал пішіні ретіндегармоникалары айнымалы бейстационар орталық дененің тартылыс өрісіндегі материялық нүктенің канондық қозғалыс теңдеулер жүйесінің интегралданатын екі жағдайының қатаң дербес шешімдері анықталып талданады;
- массасы мен өлшемі кез келген заңдылықпен өзгеретін, ал пішінінің сипаты ретіндегармоникалары белгілі шарттарға сәйкес өзгеретін бейстационар эллипсоидтың өрісіндегі материялық нүктенің ғасырлық дифференциалдық қозғалыс теңдеулерінің екі интегралданатын жағдайлары есептелінді;
- бейстационар эллипсоидтың тартылыс өрісіндегі материялық нүктенің фазалық сипаттамасы құрылып, қозғалыстың орнықтылық және орнықсыздық аймақтары табылып, олардың тек дененің бас инерция моменттерінің бастапқы мәндеріне тәуелді болатындығы анықталды;
- массасы мензоналдық гармоникасы айнымалы, ал өлшемі тербелмелі гравитациялаушы және кедергілі ортадағы эллипсоидтың тартылыс өрісіндегі материялық нүктенің Делоне аномалиясы арқылы жазылған жаңа қозғалыс теңдеуі алынып оның жуық жалпы шешімі табылған;
- табылған шешімдердің жазықтықта және кеңістіктегі графиктері көрсетілген
Дененің бастапқы шарттарына тәуелді алынған шешімдердің құрылымы және аналитикалық өрнектердің анық түрі шектелген екі дене мәселесіндегі аспан денелерінің жасанды және табиғи серігінің динамикалық эволюциясын зерттеуге мүмкіндік беретіндігі жұмыстың қолданбалы құндылығы болып табылады. Диссертациялық зерттеулерде табылған нәтижелер әртүрлі аспан механикасында кездесетін күрделі мәселелерді зерттеуде алғашқы жуық қозғалыс ретінде қабылдап, теориялық зерттеулерде қолданылуы мүмкін.
ДИССЕРТАЦИЯ ТАҚЫРЫБЫ БОЙЫНША ЖАРИЯЛАНҒАН ЖҰМЫСТАРДЫҢ ТІЗІМІ
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz