Идеал газдың кинетикалық теориясының негіздері: қысым, температура және күй теңдеуі


ИДЕАЛ ГАЗДЫҢ КИНЕТИКАЛЫҚ ТЕОРИЯСЫ
Көптеген жағдайларда біз нақты бір жүйелерді қарастыратын боламыз: бұл қайсы-бір дене немесе қайсы-бір денелер жүйесі болып табылады: осы жүйенің төңірегіндегІ қалған барлық денелер қоршаған орта деп аталады. Нақты жүйенің күйін (немесе жүйенің болу шартын) сипаттау үшін, мысалға ыдыстағы газ болсын, макроскопиялық немесе микроскопиялық көзқарастарды пайдаланамыз . Микроскопиялық сипаттау дегенімІз жүйені түзетін барлық молекулалар мен атомдардың қозғалыстарын жан-жақты қарастыру, бұл аса күрделі болып кетуі мүмкін. Бұл кинетикалық теорияның (жөне статистикалық механиканың) үлесІ болып табылады. Макроскопиялық сипаттау кезінде біз сипаттауды тікелей өлшеуге болатын шамалар арқылы береміз: оларға көлем, масса, қысым жөне температура жатады. Жүйенің күйін кез келген уақыт мезетінде анықтау үшін қажет болатын макроскопиялық айнымалылардың саны жүйенің түріне тәуелді болады. Мысалы, ыдыстағы газдың күйін сипаттау үшін үш айнымалы жеткілікті, оларға көлемді, қысымды жөне температураны алуға болады. Жүйенің күйін анықтау үшін қажет болатын осыған ұқсас шамалар күй параметрлері деп аталады.
1. 1 Идеал газ
Кезкелген зат қабылдай алатын үш агрегаттық күйлердің ең қарапайымы газ күйі болып табылады, себебі бүл кезде молекулалар арасында әсер ететін күштер өте әлсІз, белгілі жағдайларда оларды ескермей кетуге болады. Сондықтан молекулалық физиканы газдардың қасиеттерін қарастырудан бастаған ыңғайлы. Бүл жерде біз, еуелі газдағы молекула аралық күштер аз ғана емес, оларды тіптен жоқ деп санаймыз. Сонымен қатар қарапайым шарт үшін молекулалардың өлшемдерін де ескермейміз, яғни оларды материалдық нүктелер деп есептейтін боламыз. Осындай кезде газ молекулаларын еркін, өзара әрекетгеспейтін мелшерсіз бөлшектер жүйесі деп қара-стыруға болады. Молекулалар енді түзу сызықты жөне бірқалыпты қозғалатын болады. Әрбір молекула өзін ыдыста өзінен басқа молекула жоқ секілдІ сезінетін болады. Кейін, реал (нақты) газдарды қарастырған кезде бүл айтылғандардан бас тартуға тура келеді.
Өзара әрекеттеспейтін материалдық нүктелердің жиынтығының қасиеттеріндей қасиеттері бар газды идеал газ деп атайды. БіздІң бастапқы мақсатымыз осы идеал газ кинетикалық теориясын қарастыру болып табылады.
1. 2. Газдың қысымы
Ыдыста түрған газды қарастырайық. Бей-берекет қозғалыстағы газ молекулалары өзІ тұрған ыдыстың қабырғасына да, өзара да өте жақын қашықтыққа жақындайды. Осы кезде газ молекулаларының арасында немесе газ молекулалары мен ыдыстың затының молекулаларының арасында қашықтаған сайын өте тез қүлдырайтын өзара әрекеттесу күші пайда болады. Осы күштердің әсерінен газ молекулалары өздерінің бағытын өзгертеді. Бүл процесс соқтығысулар деп аталады.
Соқтығысулар газдың сипаттамаларында үлкен рөл атқарады. Оған толығырақ кейінірек тоқталамыз. Қазір біз назарымызды молекулалардың ыдыстың қабырғасымен немесе газ жанасып түрған кезкелген бетпен соқтығысуларына аударамыз. Міне, газ молекулаларының және қабырғаның осы өзара әрекеттесуі газ тарапынан қабырғаға эсер ететш және оған теңбе-тең, бағы-ты жағынан қарама-қарсы, қабырға тарапынан газға эсер етілетін күшті анықтайды. Қабырғаға газ тарапынан эсер ететін күштің мөні қабырғаның ауда-ны неғүрлым үлкен болса, ол да солғүрлым үлкен болады. Міне, қабырғаның осы ауданы тәрізді кездейсоқ шамаға төуелді болмас үшін газдың қабырғаға әсерін күш арқылы емес, қысым аркылы, яғни ыдыстың бетінің бірлік ауданына перпендикуляр түсірілген ғ күштің шамасымен сипатгау қабылданған:
Газдың өзі түрған ыдыстың қабырғасына қысым түсіруі газдың негізгі қасиеттерінің бірі. Газдың бар-жоғын көбіне оның осы қысымы арқылы ғана анықтауға болады. Сондықтан да қысым газдың ең басты сипаттамапарының бірі болып табылады.
Газдың ыдыстың қабырғасына түсіретін қысымы газ молекулаларының ыдыс қабырғасымен сансыз-көп соқтығысуларының нәтижесі болып табылады. Молекулалардың осындай соқтығысуларының нәтижесінде ыдыс қабырғасының материалының бөлшектері ығысады, яғни деформцияланады. Деформацияланған қабырға, әрбір нүктеде қабырғаға перпендикуляр бағытталған серпімді күшпен газға эсер етеді. Бүл күш шама жағынан газдың кабырғаға түсіретін күшіне тең де, ал бағыты жағынан оған қарама-қарсы болады.
ӘрбІр жеке молекуланын қабырға молекулаларымен әрекетгесу күшінің шамасы белгісіз болса да, механика заңдарына сүйене отырып, газдың барлық молкеулалардың қозғалысынан туған орташа күшті, яғни қысымды табуға болады екен.
Газ параллелипед түріндегі ыдыста болсын, әрі газ тепе-тендік күйде делік. Бүл берілген уакытта газ ыдыс қабырғаларына катысты тұтастай алғанда тынышгыкта деген сөз: қайсы-бір алынған бағытга қозғалатын
молекулалар саны орташа есеппен жылдамдықтары карама-карсы жақка бағытталған молекулалар санына тең.
Газдың ыдыстың бір қабырғасына, мысалға, оң жақ abcd бүйір қабырғасына түсіретін қысымын есептеп шығарайық, x координат осін параллелепипедтің abcd қа-бырғасына перпендикуля рқырының бойымен бағыттайық (1. 1-сурет) . V жылдамдықтар қалай бағытталса да, бізге керегі тек молекулалар жылдамдығынын х өстегі V х
қүраушылары ғана abcd қабырғаға қарай молекулалар тек V х жылдамдыкпен ғана қозғалады.
Қарастырылмақ қабырғаға жанай жатқан қалындығы Δ х газ қабатын ойша бөліп алайық. Оған деформацияланған қабырға тарапынан серпімді күш Ғәсер етеді. Абсолют шамасы жағынан дәл осындай күшпен газ да қабрғаға әсер етеді. Ньютонның екінші заңы бойынша күш импульсы ҒΔt (мұндағы t - қайсы-бір уақыт аралығы) біздің қабаттағы газ импульсының өзгерісіне тең болады. Газ тепе-тендік күйде, сондықтан газ күш импульсы бағытында (х өсінің оң бағытына қарсы бағытта) ешқандай импульс өсімшесін қабылдамайды.
Газ молекулаларының ретсіз қозғалысы кезінде уақыттың ішіңде біздің қабатқа солдан оңға қарай молекулалардың қайсы бір
саны кіріп, молекулалар-дың сонша саны одан кері бағытта, оңнан солға қарай, шығады. Кіретін молекулалар өздерімен бірге белгілі импульс мөлшерін ала кіреді. Шығатын молекулалар өздерімен бірге карсы таңбалы дәл осындай импульс мөлшерін ала кетеді де, қабаттың алған импульсы қабатка кіретін және одан шығатын молекулалардың импульстерінің алгебралық қосындысына тең болады.
Біздің қабатқа
уақыттың ішінде сол жақтан келіп кіретін молекулалар санын есептеп шығарайық.
Осы уақыттың ішінде
шекаралыққа сол жақтан оданшама-
сынан аспайтын қашықтықта орналасқан молекулалар келіп жете алады. Олардың барлығы да табанының ауданы
және үзындығы
5олатын параллелепипедтің көлемінде, яғни
көлемде орналасқан.
Егер көлем бірлігінде п молекулалар болатын болса, онда көрсетілген көлемде nS V х Δt молекулалар болады. Бірақ олардың тек жартысы ғана солдан оңға қарай қозғалып, біздің қабатқа келіп түседі, олардың екінші жартысы одан кері қозға-лып, қабатқа келіп кірмейді. Демек, Δt уақытта қабатқа солдан оңға қарай
молеулалар келіп кіреді. Бүл молекулалардың әрбіреуінің тV х
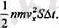
импульсы болады (m - молекуланың массасы), ал олардың қабатқа алып келетін жалпы импульсы:
Осы уақыттың ішінде оңнан солға карай қозғала отырып, қабатты кері таңбалы жалпы импульсі дәл сондай болатын молекулалардың дөл сондай саны тастап кетеді. Сөйтіп, қабатқа оң импульсты молекулалардың келіп
жоне одан терІс импульсты молекулалардың кетуіне байланысты қабаттағы импульстың жалпы өзгерісі мынандай болады:
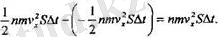
Бүл ҒΔt ( күш импульсының өсерінен болуға тиісті өзгерісті көрсетеді сондықтан былай деп жаза аламыз:
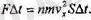
Осы тендіктің екі жағын да шамасына SΔt бөлсек, онда
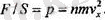 (1. 1)
(1. 1)
Осы кезге дейін біз газдың барлық молекулаларының жылдамдығынын у х проекциясы бірдей деп келдік. Шын менісінде олай емес екендігі анық. Молекулалардың V жылдамдықтары да, олардың осіндегі проекциялары да түрліше молекулаларда түрліше болатындығы анық. Молекулалардың жыл-дамдықтарының жөне олардың координаттар осіндегі болатындығын ескеріп, (1. 1) өрнекке кіретін
шамасын оның
орташа мэнімен алмастырамыз, сөйтіп (1. 1) өрнекті мына түрге келтіреміз:
(1. 2)
Әрбір молекуланың V жылдамдығы үшін былай деп жазуға болады:
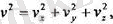
сондықтан
(1. 3)
(соңғы тендІк орталау амалы мен қосу амалының орындарын алмастыруға болады дегенді білдіреді) . Молекулалық қозғалыстың толық ретсіздігінен жылдамдықтардың үш координат өстеріне проекцияларының квадратгары-ның орташа мөндері бір-біріне тең деп алуға болады, яғни,
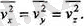
Ал бүл дегеніміз (1. 2) өрнекті еске алсақ, онда
= V 2 /3 дегенді білдіреді. Мүны апарып (1. 2) өрнекке қойсақ, онда мынаған келеміз:
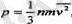
немесе теңдіктің оң жағын екіге бөліп жөне көбейтсек, онда
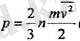 (1. 4)
(1. 4)
Осы келтірілген қарапайым болжау ыдыстың кез-келген қабырғасы үшін және газ ішінде орналастыруға болатын кез-келген ауданша үшін орындалады. Бірақ басқа жағдайларда да біз (1. 4) өрнекте көрсетілген мөнге келеміз, (1. 4) ернектегі шама газдың бір молеуласыныц орташа кинетика
лық энергиясы /иу 2 /2 болып табылады, демек, газдың қысымы бірлік көлем-дегі молекулалардың орташа кинетикалық энергиясының үштен екісіне тең болады екен.
Бүл идеал газдың кинетикалық теориясының аса маңызды қортындыла-рының бірі болып табылады. (1. 4) өрнек молекулалық, яғни бір молекулаға қатысты шамалар мен газды тұтастай сипаттайтын тәжірибеде тікелей олше-уге болатын макроскопиялық болып табылатын қысым шамасы арасындағы байланысты тағайындайды. (1. 4) орнегін идеал газдардың кинетикалық теориясының негізгі теңдеуі деп атайды.
Газдың қысымының оның молекулаларының орташа кинетикалыц энергиясымен анықталатынына ерекше назар аудару керек, Бүл дегеніміз газдың қысымы газдың молекулалардың орасан зор санынан түратындығымен байланыстылығын көрсетеді. Бір немесе бірнеше молекуланың тудыратын қысымы жайлы айтудың ешбір мағынасы жоқ. Көп бөлшектерден тұратын системалар үшін ғана мағынасы болатын шамалар жайлы айтқанда, олар статистикалық сипатта дейді.
Қысымның ХЖ дегі өлшем бірлігі ньютон/м 2 болып табылады. Бүл бірлік паскаль деп аталады (Па) .
1. 3 Температура
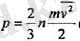 (1. 4)
(1. 4)
теңдеуден идеал газ қысымының оның тығыздығына (газдың тығыздығы бІрлік көлемдегі молекулалардың п санымен анықталады) жөне молекулалардың ілгерілемелі қозғалысының орташа кинетикалық энергиясаелелді болатындығы шығады. Түрақты п, демек, түрақты V кезінде (п = N/V, мүндағы N- ыдыстағы молекулалардың саны) газдың қысымы молекулалардың тек орташа кинетикалық энергиясына ғана төуелді болады.
Тәжірибеден білетініміздей, түрақты қысым кезінде газдың қысымын тек бір ғана жолмен, оны қыздыру немесе суыту арқылы ғана озгертуге болады: газды қыздырған кезде оның қысымы артады, ал суытқан кезде қысымы ке-миді. қыздырылған немесе суытылған газ өзінің температурасымен сипатта-лады. Демек, орташа кинетикалық энергия мен қысымның арасында (1. 4) түрінде байланыс бар.
Температура дегеніміз денелердің жылулық тепе-тендік күйін сипаттайтын физикалық шама: жылулық тепе-тендіктегі денелердің температура-лары бірдей болады. Керісінше, температуралары бірдей денелер бір-бірле-рімен жылулық тепе-тендікте болады. Егер қандай да бір, екі дене үшінші денемен жылулық тепе-тендікте болатын болса, онда бүл екі денелер де өзара жылулық тепе-тендікте болады. Бүл аса маңызды тоқтам табиғаттың негізгі зандарының бірі болып табылады. Температураны өлшеу мүмкіншілігі міне осыған негізделген.
Температураны өлшеу үшін дененің температурасын өзгерткенде оның қасиеттерінің озгеретіндігін пайдаланады. Демек, осы қасиеттерді сипаттайтын шамалар да өзгереді. Сондықтан температураны олшейтін аспапты, яғни термометрді жасаған кезде қайсы-бір затты (термометрлік затты) және зат-тың қасиетін сипаттайтын белгілі бір шаманы (термометрлік шаманы) таң-дап алады. Түрмыста пайдаланып жүрген термометрлерде термометрлік зат сынап та, ал термометрлік шама - сынап бағанының үзындығы.
Температураның шамасына сандық мәндерді сәйкестеу үшін термометрлік шаманың температураның шамасына тәуелділігін тағайындау керек. Түрмы-стық сынап термометрлерінде бүл - сынап бағанының үзындығының темпе-ратураға сызықтық төуелділігі.
Енді температураның бірлігі - градусты тағайындау керек. Градустың шамасы былайшатағайындалады. Екі температураны тандап алады (реперлік нүктелер деп аталады) - кобіне бүл атмосфералық қысым кезінде мұздың еру температурасы және судыц қайнау температурасы жөне осы температура интервалын тең бөліктерге - градустарға бөледі. Осы температуралар-дың біреуіне белгілі сандық мөн береді. Сойтіп, екінші температураның мөні және кезкелген аралық температуралардың мәндері тағайындалады. Осылай-ша температуралық шкалаға келеді.
Осы заманғы термометрия газ термометрінің комегімен тағайындалатын идеал газ шкаласыиа негізделген. Газ термометрі деп отырғанымыз идеал газбен толтырылған және газдың қысымын олшеуге арналған манометрмен
жабдықталған жабық ыдыс болып табылады. Мүндай термометрде термометрлік зат дегеніміз идеал газ да, ал температурага тәуелділігін сызықтық деп алады. ОсындаЙ кезде судың қайнау температурасы кезіндегі қысым (р қ ) мен мүздың еру температурасы кезіндегі қысымның (р0 қатынасы осы тем-пературалардың өздерінің қатьшасына тең болады:
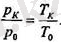
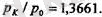
Демек, температуралардың қатынасы да осылай болады:
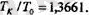
Градустың шамасын тағайындаған кезде айырымын 100- ге бөледі:
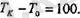
қатынасын тәжірибеден жеңіл анықтауға болады. Ол мынаны береді:
Соңғы екі теңдіктен қабылданған шкалада мүздың еру температурасы дегенІміз 273, 15 градус болып шығады, ал судың қайнау температурасы болса, ол 373, 15 градус екен. Газ термометрдің көмегімен қайсы-бір дененің температурасын өлшеу үшін денені газ термометрмен жанастыру керек, сосын тепе-тендікке жеткеннен кейін термометрдегі газдың р қысымын өлшейді. Сонда дененің Т температурасы
Техникада және өмірде мұздың еру температурасын нөл деп алатын Цельсий шкаласы пайдаланылады. Бұл шкала бойынша анықталған { температура абсолюттік Т температурамен мынандай байланыста болады:
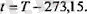
Бүдан әрі біз Кельвин шкаласын пайдаланатын боламыз.
Сонымен, температура дегеніміз денелердің жылулық тепе-тендігін сипаттайды екен: тепе-тендік күйге еткен кезде денелердің температуралары теңеседі де, тепе-тендік күйде түрған дененің немесе денелер системасының барлық бөліктерінің температуралары бірдей болады. Температураны өлшеу процедурасының езі осымен байланысты.
Жылулық тепе-тендік орнау процесі энергия алмасу арқылы өтеді. Бірақ энергетикалық тепе-тендік бүкіл газ үшін орнамайды, тек бір молекулаға қаты-сты алынған орташа кинетикалық энергия үшін ғана орындалады. Молекула-ның ілгерілемелі қозғалысының мІне, осы орташа кинетикалық энергиясы өзін температура төрізді үстайды.
Бүл екі шаманың арасындағы тағы бір үқсастық - кинетикалық энергия да температура тәрізді аддитивтік шама емес, ол да барлык газ үшін жөне оның бөлІктері үшін (жеткілікті молекулалар саны болатын) бірдей болады. Түгел газдың энергиясын алатын болсақ, ол - аддитивтік шама, ол газдың бөліктерінің энергияларының қосындысынан түрады.
Осы айтылғандардан температура деген шама молекулалардың ілгеріле-мелі қозғалысының орташа кинетикалық энергиясы деген тоқтамға келуге болады. Сонымен, егер
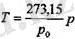
өрнекпен анықталады, мүндағы р 0 - еріп жатқан мүзға қойылғаи термометр-дегі газдың қысымы.
Практикада газ термометрін сирек қолданады. Оның ролі басқа да - оның көмегімен пайдаланылып жүрген барлық термометрлер градуирленеді.
Біздің шкаламыз бойынша нөлге тең болатын температураның идеал газ-дың қысымы нөлге тең болатын температура екендігінде сөз жоқ. Егер тем-пературалык шкаланың нолі кезінде термометрлік шама нөлге айналатыи болеа, онда мүндай шкала абсолютгік шкала деп аталады, ал осындай шкала бойынша саяалған температура абсолюттік температура деп аталады. Осы жерде сипатталған газ термометрінің шкаласы абсолюттік деп аталады. Оны кебіне Кельвин шкаласы деп те атайды, бүл шкала бойынша температура бірлігі кельвин деп аталады жене К деп белгіленеді.
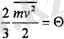
деп жазатын болсақ, онда (1. 4) ернек ықшам жазылатын болады:
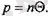
Температураны үйреншікті бірліктермен өлшей беру үшін градустарды энергияның олшемділігімен байланыстыра алатын қажетті коэффициент енгізу керек. Ол коэффициентті
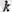 арқылы белгілейді. Сонда градустармен алы-нған
арқылы белгілейді. Сонда градустармен алы-нған
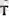 температура мен орташа кинетикалық энергия арасында мынандай байланыс болады:
температура мен орташа кинетикалық энергия арасында мынандай байланыс болады:
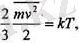
осыдан:
(1. 5)
Энергия бірлігі мен температура бірлігі кельвин арасындағы қатынасты анықтайтын к коэффициент Больцман тұракгысы деп аталады. СИ-дегі оның мөні
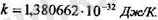
Температура молекулалардың ілгерлемелі қозғалысының орташа энерги-ясы болып анықталатындықтан, ол да қысым төрізді статистикалық шама болып табылады.
1. 4. Идеал газ күйінің тещдеуі
Молекулалык-кинетикалық көзқарастар және солардың негізінде алын ған теңдеулер газ кұйін анықтайтын шамаларды өзара байланыстыратын қаты-настарды табуға мүмкіндік береді. Бүл шамаларға газдың р қысымы, оның
Т температурасы және газдың белгілі массасын алатын V колем жатады. Оларды күй параметрлері деп атайды.
Бұл аталған үш шама өзара төуелсіз емес. Олардың өрбіреуі қалған еке-уінің функциясы болып табылады. Осы үш шамаларды - газдың белгілі мас-сасы үшін оның қысымын, көлемін және температурасын байланыстырып түратын тендеуді күй теңдеуі деп атайды және оны жалпы түрде
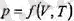
деп жазады.
Идеал газдар үшін күй тендеуін кинетикалық теорияның негізгі (1. 4) және (1. 5) тендеулерінен жеп-жеңіл алуға болады. Егер (1. 4) тендеуге молекула-лардың орташа кинетикалық энергиясының орнына оның (1. 5) тендеудегі мәнін қоятын болсақ, онда:
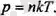

Егер V көлемде болшектер саны N болатын болса, ондаоны
апарып (1. 6) өрнекке койсақ, мынаған келеміз:
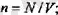
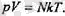
Ьүл тендеуге барлық үш күй параметрлері де кіреді, сондықтан да ол идеал газ күйінің тендеуі болып табылады.
Мүндағы тікелей елшеуге келмейтін
болшектер санының орнына жеңіл
өлшеуге болатын газ массасын енгізген тиімдірек болады. Бүл үшін моль түсінігін пандаланатын боламыз. Моль деп көміртегініц изотопының 0, 012 кг массасы қанша қүрама элменттерден түратын болса, сонша қүрама элементтерден (атомдардан немесе молекулалардан) тұратын кезкелген заттың мөлшерін атайды. Сонымен кезкелген заттың бір молінде молекула (атомдардың) бірдей саны болады екен. Егерде қайсы-бір екі заттың салыстырмалык; массаларын
және
деп, ал осы заттардың молекулаларының массаларын
жөне
деп белгілеп,
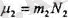
(1. 8)
деп жаза аламыз, мүндағы
жөне
-осы заттардың моліндегі бөлшек-тер саны. Салыстырмалық массалардың анықтамасынан
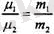
екендігі шығады, сондықтан (1. 8) өрнектегі бірінші тендікті екінші теңдікке бөлетін болсақ, онда
екендігіне келеміз, яғни кезкелген зат-
тың молінде молекулалардың бірдей саны болады екен.
Барлық заттар үшін бІрдей болатын бір молдегі болшектер саны Авогад ро саны деп аталады. Оны
деп белгілейтін боламыз. Егер берілген зат-тың массасы
молекулалардан түратын болса, онда заттың берілген массасында оның қанша молі бар екендігін білу үшін
деп алсақ болтаны;
бүл қатынас бізге заттың молдерінің
санын береді:
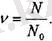
Егер осы қатынастың алымын да, бөлімін де молекуланың
массасына
көбейтіп,
- берілген заттың массасы да, ал
- заттың
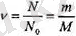
болатындығын көреміз. Осыдан
деп алып, оны (1. 7) теңдікке қойсақ, онда:
бір молінің массасы екендігін ескерсек, онда
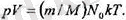
Бүл теңдікке екі универсаль түракты кіреді; Л^ Авогадро саны жөне к Больцман түрақтысы. Осы екі универсаль түрақтылардың көбейтіндісінR деп белгілейді және ол универсал газ түрақтысы болып табылады. Оның XЖ дегі мәні R - 8, 31 Дж/моль. К. Енді идеал газ күйінің теңдеуІн былай деп жаза аламыз:
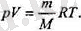 ` (1. 9)
` (1. 9)
Газдың бір молі үшін бұл теңдеу былай жазылады.
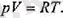 (1. 10)
(1. 10)
... жалғасы1. 5. Идеал газ заңдары
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz