Жиындар және негізгі амалдары: Эйлер-Венн диаграммалары, декарттық көбейтінді және қосынды мен көбейтінді ережелері


М А З М Ұ Н Ы
КІРІСПЕ . . . 3
І ТАРАУ
1 Жиындар және оларға қолданылатын амалдар
1. 1 Жиындар . . . 5
1. 2 Жиындардың берілу тәсілдері. Ішкі жиындар. Тең жиындар. Эйлер -Венн диаграмммалары . . . 6
ІІ ТАРАУ
2. 1 Жиындардың қиылысуы. Жиындардың бірігуі . . . 9
2. 3 Ішкі жиынға толықтауыш жиын. Жиындардың айырмасы. Екі жиынның декарттық көбейтіндісі . . . 12
ІІІ ТАРАУ
3. 1 Қосынды және Көбейтінді ережелері . . . 16
3. 2 Қайталанатын орналастырулар. Алмастырулар. Орналастырулар . . . 17
3. 4 Терулер. Терулер санының кейбір қасиеттері . . . 20
Пайдаланылған әдебиеттер тізімі . . . 23
Кіріспе
Математикада XIX ғасырдың екінші жартысында жиын ұғымы пайда болды. Жиын ұғымының математикаға енуі жиын теориясын қалыптастырды. Жиын теориясының негізін қалаушы неміс математигі Георг Кантор (1845-1918) болды.
Белгілі бір ортақ қасиеттерге ие болып, белгілі бір заңдылықпен біріккен нәрселер, объектілер жиын құрайды. Мысалы: аспандағы жұлдыздар жиыны, кітап бетіндегі әріптер жиыны, бөлімі 6 саны болатын дұрыс бөлшектер жиыны т. с. с.
Жиындар элементтерден құралады. Жиындардың элементтері аталып беріледі немесе сол жиын элементтеріне ғана тән қасиет (белгі) көрсетіледі. Жиынды латынның бас әрпімен белгілеп, оның элементтерін фигуралық жақшаның ішіне алып жазу келісілген. Мысалы, “планета” сөзіндегі әріптер жиынын P әрпімен белгілесек, P={а, п, н, л, е, т} немесе P={т, п, н, л, е, а} элементтер ретін әр-түрлі жазуға болады.
Жиындар шектеулі жиын, шектеусіз жиын болып бөлінеді. Мысалы, цифрлар жиыны A - шектеулі жиын, оған 10 элемент енеді. A={0, 1, 2, 3, 4, 5, 6, 7, 8, 9} жиынының элементтер санын көрсетіп жазсақ: n(A) =10. Ал натурал сандар жиыны N - шектеусіз жиын.
Егер a элементі B жиынына тиісті болса, оның жазылуы: a Є B. Оқылуы: “a B жиынының элементі” немесе “a B жиынына тиісті”.
Мысалы, 7 саны натурал сандар жиынына тиісті: 7 Є N.
Егер c элементі A жиынына тиісті болмаса, оның жазылуы: c ¢ A. Оқылуы:”c A жиынына тиісті емес”. Мысалы, 0 саны натурал сандар жиынына тиісті емес: 0 ¢ N.
Егер жиында бірде-бір элемент болмаса, оны бос жиын деп атайды. Бос жиынның белгіленуі: Ø . Мысалы, 74 және 79 сандарының арасындағы жай сандар жиыны - бос жиын. Әріптер жазылмаған дәптер бетіндегі әріптер жиыны - бос жиын.
Егер B жиынының әрбір элементі A жиынына тиісті болса, онда B жиыны A жиынының ішкі жиыны деп аталады. Мысалы, A={1, 2, 3, 4, 5, 6, 7} жиынындағы жұп сандар жиыны - B={2, 4, 6}. B жиынының әрбір элементі A жиынына тиісті. Белгіленуі: B Є A. Оқылуы: B жиыны - A жиынының ішкі жиыны. Жиындардың байланыстары мен арақатынастары Эйлер-Венн дөңгелектері арқылы кескінделеді.
Суретте B жиыны A жиынының
ішкі жиыны екені Эйлер-Венн
дөңгелектері арқылы кескінделген. Бос жиын кез келген жиынның ішкі жиыны болады. Белгіленуі: Ø Є A. Мұндағы A - қандай да бір жиын.
І ТАРАУ. ЖАЛПЫ ҰҒЫМДАР
1. Жиындар және оларға қолданылатын амалдар
1. 1 ЖИЫНДАР
Жиын ұғымы - анықтауға болмайтын алғашқы ұғымдардың бірі. Жиын ұғымының орнына күнделікті өмірде «жиынтық», «коллекция», «табын», «отар» т. с. с. сөздерді де қолдана береді. Жиын деп ортақ қасиеттері, белгілері бойынша біртұтас етіп біріктірілген объектілерді (нәрселерді) айтуға болады. Жиынды құрайтын объектілерді жиынның элементтері дейді. Жиындарды латынның бас әріптерімен, оның элементтерін кіші әріптерімен белгілейді.
Жиын мен оның элементтерінің арасындағы қатысты «тиісті», немесе «жатады» деген сөздермен беруге болады да, былай белгілейді Î. Мысалы, « а объектісі А жиынына тиісті» деген сөйлемді былай жазып көрсетеді: а Î А . Бұл сөйлемді былай да оқуға болады: « а элементі А жиынына жатады», « в элементі А жиынына тиісті емес» деген сөйлемді былай жазып көрсетеді: b А, кейде b Ï А .
Мысалы, егер А - жұп натурал сандар жиыны болса, онда
4 Î
А,
7 Ï
А,
16 Î
А,
27 Ï
А,
105 Ï
А,
1
 Ï
А
Ï
А
Жиындар шекті, шексіз, бос жиын болуы да мүмкін.
Элементтерінің саны белгілі бір саннан артық болмаса, онда ондай жиындар шекті болғаны. Мысалы, күн жүйесіндегі планеталар жиыны, қазақ алфавитіндегі әріптер жиыны, бір кесек бордағы молекулалардың жиыны, мұхиттардағы балықтар жиыны т. с. с. шекті жиындар.
Түзудің бойындағы нүктелер жиыны, әлемдегі жұлдыздар жиыны, натурал сандар жиыны т. с. с. шексіз жиындар.
x² + 1 = 0 теңдеуінің нақты түбірлерінің жиыны, айды мекендейтін адамдар жиыны т. с. с. бос жиындар. Сонымен бірде-бір элементі болмайтын жиынды бос жиын деп атайды да былай белгілейді: Ø.
Кейбір сандық жиындардың арнаулы таңбалары бар. Барлық натурал сандар жиыны
Ν =
{1, 2, 3, . . . ,
п, . . .
}; барлық теріс емес бүтін сандар жиыны
Ζ
0
= {0, 1, 2, 3, . . . ,
п. .
. }; барлық бүтін сандар жиыны
Ζ
= { . . . , -3, -2, -1, 0, 1, 2, 3 . . . }; барлық рационал сандар жиыны
Q
, әрбір рационал санды қысқартылмайтын бөлшек түрінде
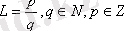 жазуға болады; барлық иррационал сандар жиыны
I
; барлық нақты сандар жиыны
R
әріптерімен белгіленеді. Аталған сандық жиындардың бәрі шексіз жиындар.
жазуға болады; барлық иррационал сандар жиыны
I
; барлық нақты сандар жиыны
R
әріптерімен белгіленеді. Аталған сандық жиындардың бәрі шексіз жиындар.
Кейде жиынның элементінің өзі де жиын болады. Мысалы мектептегі сыныптар жиыны. Бұл жиынның элементі - сынып, ал сыныптың өзі оқушылардың жиыны. Жалғыз элементтен тұратын да жиын болады. Мысалы 2 x = 10 теңдеуінің түбірлерінің жиыны 5.
1. 2 ЖИЫНДАРДЫҢ БЕРІЛУ ТӘСІЛДЕРІ. ІШКІ ЖИЫНДАР. ТЕҢ ЖИЫНДАР. ЭЙЛЕР-ВЕНН ДИАГРАММАЛАРЫ
Егер кез келген объектінің жиынға жататыны не жатпайтыны туралы айта алсақ, онда жиын берілді дейміз. Жиынды оның элементтерін атап шығу арқылы беруге болады. Мысалы жиын 1, 2, 3, 4, 5 сандарынан тұрса, ол жиынды былайша жазып көрсетеді А = {1, 2, 3, 4, 5}.
Осы жиынды басқаша да тәсілмен беруге болады А = { x / x Î N , x < 6}. Мұнда жиынның элементтерінің сипаттамалық қасиеті көрсетілген, яғни 6-дан кем барлық натурал сандар жиыны берілген. Бұл жиын екінші тәсілмен беріліп тұр, атап айтқандк жиынның элементтері натурал сандар және 6-дан кіші болу қасиеттері көрсетілген. Жиынды осы тәсілмен бергенде фигуралы жақшада оның элементі көрсетіліп, тік сызықтан кейін жиынның элементтерінің сипаттамалық қасиеті жазылады.
Элементтерінің саны аса көп болмаған жағдайда шекті жиындарды бірінші тәсілмен беруге болады. Ал, екінші тәсілмен шекті және шексіз жиындарды да беруге болады. Мысалы, М = { x / x Î R , 3 < x < 12} жиынын бірінші тәсілмен бере алмаймыз, өйткені ол шексіз жиын.
А
- қазақ алфавитіндегі дауысты дыбыстар жиыны болсын, яғни
А
={
а, ә, е, э, е, о, ө, ұ, ү, ы, і, у, и
}.
В
- жуан дыбыстар жиыны болсын, яғни
В
={
а, о, ы, ұ, у, и
}. Сонда
В
жиыны
А
жиынының ішкі жиыны болады да,
В
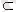 А
символымен жазылады.
А
символымен жазылады.
Анықтама. Егер В жиынының кез келген элементі А жиынының да элементі болса, онда В жиыны А жиынының ішкі жиыны деп аталады.
Бос жиын кез келген жиынның ішкі жиыны болады. Сол сияқты жиынның өзі де өзіне ішкі жиын болады, яғни Ø
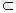 А
;
А
А
;
А
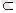 А.
А.
А -ның өзі және Ø жиын меншіксіз ішкі жиындар деп аталады. Ал, А жиынының басқа ішкі жиындары, егер олар бар болса, меншікті ішкі жиындар деп аталады.
Мысалы А={a, b, c} жиынының алты меншікті ішкі жиындары {a}, {b}, {c}, {a, b}, {a, c}, {b, c} және екі меншіксіз ішкі жиындары Ø {a, b, c} бар.
Анықтама. Егер А мен В біріне-бірі ішкі жиын болса, онда олар өзара тең жиындар деп аталады, яғни А
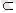 В және В
В және В
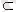 А болса, онда А=В.
А болса, онда А=В.
Жиын және ішкі жиын ұғымдарын көптеген математика ұғымдарын анықтағанда қолданады. Мысалы геометриялық фигура деп кез келген нүктелер жиынын айтады. Бұдан, бір элементі жиын да болатындықтан жеке алынған нүкте де геометриялық фигура екенін көреміз. Егер F1 фигурасы F2 фигурасының меншікті ішкі жиыны болса, онда F1 фигурасы F2 фигурасының бөлігі деп аталады. Мысалы, АВ кесіндісі АВ түзуінің бөлігі.
Жиындарының арасындағы қатынастарды Эйлер-Венн диаграммасы (дөңгелегі) * арқылы кескіндеп көрсетуге болады. Егер А мен В жиындарының ортақ элементтері болып, бірақ бірі екіншісінің ішкі жиыны болмаса, онда оларды 1-суреттегідей кескіндейді. Ешқандай ортақ элементтері жоқ А және В жиындарын 2-суреттегідей кескіндейді. Егер В жиыны А жиынының ішкі жиыны болса, онда 3-суреттегідей кескіндейді. Тең жиындарды 4-суреттегідей кескіндейді.
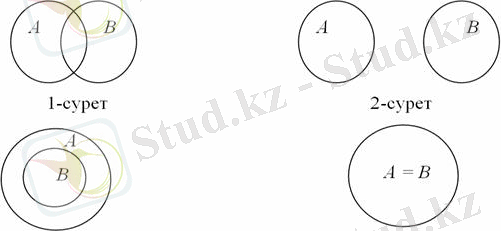
3-сурет 4-сурет
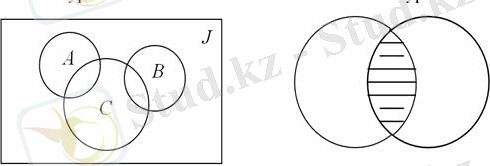
5-сурет 6-сурет
Кейде бір J жиынының ішкі жиындарын қарастыруға туру келеді. Мұндай J жиынын универсал жиын деп атайды. Мысалы - A - Шығыс Қазақстан мемлекеттік университетінің бірінші курс студенттерінің жиыны, B - осы университеттің екінші курс студенттерінің жиыны, C - осы университеттің спортпен шұғылданатын студенттерінің жиыны болсын, сонда J жиыны осы университеттің барлық студенттерінен тұрады, өйткені A
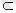 J, B
J, B
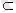 J, C
J, C
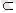 J (5-сурет) .
J (5-сурет) .
Эйлер-Венн диаграммасында универсал J жиынын тік төртбұрыш арқылы, оның ішкі жиындарын дөңгелектер арқылы кескіндейді.
ІІ ТАРАУ
2. 1 Жиындардың қиылысуы. Жиындардың бірігуі
A= { a; b; c; d } және B = { c; d; e } жиындары берілсін. Осы жиындардың екеуіне де ортақ болатын элементтерден тұратын C = { c; d } жиынын құрайық. Сонда осы С жиыны А мен В жиындарының қиылысуы болады.
Анықтама. А мен В жиындарының қиылысуы деп А жиынында да, В жиынында да жататын элементтерден және тек солардан ғана тұратын жиынды айтады. А мен В жиындарының қиылысуы А Ç В өрнегімен белгіленеді, Ç таңбасы жиындардың қиылысу белгісі.
А Ç В жиынында жататын кез-келген х элементі А мен В жиындарында да жататын болғандықтан, анықтаманы былай жазып көрсетуге болады: А Ç В ={ х/х Î А , х Î В }.
Егер А және В жиындарының ортақ элементтері болмаса, онда олар қиылыспайды, яғни А Ç В = Æ түрінде жазады. Мысалы, бір таңбалы натурал сандар мен екі таңбалы натурал сандар жиындары қиылыспайды.
Егер А және В жиындарының кемінде бір ортақ элементі болса, онда олар қиылысады дейді, яғни А Ç В ¹ Æ түрінде жазады.
6-суретте А Ç В жиыны штрихталған аудан арқылы көрсетілген.
Қиылысу амалының қасиеттеріне тоқталайық.
1. Кез келген А және В жиындары үшін қиылысу амалының коммутативтік (орын ауыстырымдылық) заңы орындалады, яғни А Ç В = В Ç А .
Бұл теңдіктің дұрыстығы тікелей анықтамадан туындайды.
2. Кез келген А, В және С жиындары үшін қиылысу амалының ассоциативтік (терімділік) заңы орындалады, яғни (( А Ç В ) Ç С = А Ç ( В Ç С ) ) .
а) ( А Ç В ) Ç С жиынының х кез келген элементі болсын дейік. Сонда, жиындардың қиылысуының анықтамасынан, х Î А Ç В және х Î С бұдан х Î А, х Î В, х Î С, яғни х Î А және х Î В Ç С, бұдан х Î А Ç ( В Ç С ) . Сонымен, ( А Ç В ) Ç С жиынының кез келген х элементі А Ç ( В Ç С ) жиынында да жатады, яғни ( А Ç В ) Ç С Ì А Ç ( В Ç С ) .
б) Енді А Ç ( В Ç С ) жиынында жататын кез келген у элементін алайық. у Î А Ç ( В Ç С ), бұдан у Î А, у Î В Ç С қиылысудың анықтамасынан у Î А, у Î В, у Î С, яғни у Î ( А Ç В ) Ç С . Сонымен, А Ç ( В Ç С ) жиынында жататын кез келген у элементі ( А Ç В ) Ç С жиынында да жататын болды. Демек, А Ç ( В Ç С ) Ì ( А Ç В ) Ç С .
Тең жиындардың анықтамасы бойынша, А Ç ( В Ç С ) = ( А Ç В ) Ç С деген қорытындыны жасаймыз.
3. Егер В Ì А, онда А Ç В = В .
Шындығында, егер В жиыны А жиынының ішкі жиыны болса, онда бұл жиындар 3-суреттегідей кескінделеді, яғни В және А жиындарының ортақ элементтері В жиынының элементтерінен тұрады, демек А Ç В = В .
Кез келген А жиыны үшін мына қатынастар орынды болады: А Ç А = А , А Ç Æ = Æ, А Ç I = А .
A = { m; n; p; k; l } және B = { p; r; s; n } жиындары берілсін. Кемінде осы жиындардың біріне жататын элементтерден тұратын жиын құрайық, яғни С = { m; n; p; k; l; r; s }. Міне, осы жиынды екі А және В жиындарының бірігуі дейді.
Анықтама. А мен В жиындарының бірігуі деп кемінде біреуінде жататын элементтерден және тек солардан ғана тұратын жиынды айтады. Жиындардың бірігуі А В өрнегімен белгіленеді.
А және В жиындарының бірігуін қысқаша мынадай теңдікпен беруге болады: А В = { x / x А немесе x В }. 7-суретте А В жиыны штрихталған ауданмен кескінделген.

7-сурет
Жиындардың бірігуі амалының қасиеттеріне тоқталайық.
1. Жиындардың бірігуі коммутативті, яғни А В = В А.
2. Кез келген А, В және С жиындары үшін бірігудің ассоциативтік заңы орындалады ( А В ) С = А ( В С ) .
Екінші қасиетін дәлелдейік.
1. ( А В ) С жиынында жататын кез келген х элементін алайық, яғни х ( А В ) С , бұдан бірігудің анықтамасы бойынша х А В немесе х С.
а) х А В болсын, бұдан х А немесе, х В . Егер х А, онда бірігудің анықтамасы бойынша х А ( В С ) . Егер х В, онда х В С, бұдан х А ( В С ) . Сонымен, х А В шартынан х А ( В С ) екенін көрдік.
б) Енді х С , бұдан х В С сондықтан х А ( В С ) .
Сонымен, ( А В ) С жиынының кез келген х элементі А ( В С ) жиынында да жататын болды, демек ( А В ) С А ( В С ) .
2. Енді А ( В С ) жиынында жататын кез келген у элементін алайық, яғни у А ( В С ) . Сонда бірігудің анықтамасынан, у А немесе у В С .
а) у А, анықтама бойынша, у А В, бұдан у ( А В ) С .
б) у В С болсын, онда бірігудің анықтамасынан, у В немесе у С . Егер у В, онда у А В, яғни у ( А В ) С . Егер у С, онда у ( А В ) С . у В немесе у С шартынан у ( А В ) С екендігі шығады.
Сонымен біз А ( В С ) жиынының кез келген элементі ( А В ) С жиынында да жататынына көз жеткіздік, демек А ( В С ) ( А В ) С .
Тең жиындардың анықтамасына сүйеніп, ( А В ) С = А ( В С ) екенін көреміз.
3. Егер В А, онда А В = А.
Кез келген А жиыны үшін мына қатынастар орынды болады:
А А = А; А = А; А J = J.
Жиындардың қиылысуы мен бірігуі амалдарының байланысын дистрибутивтік (үлестірімділік) заңы арқылы көрсетуге болады.
4. Кез келген А, В және С жиындары үшін мына теңдіктер орынды болады:
а) А ( В С ) = ( А В ) ( А С ) ;
ә) А ( В С ) = ( А В ) ( А С ) .
Дистрибутивтік қасиеттерді Эйлер-Венн диаграммалары арқылы түсіндіруге болады. Мысалы 4 ә) теңдігінің дұрыстығына көз жеткізейік.
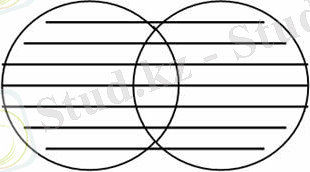
8-суретте а) диаграммасында тік сызықтармен А жиыны белгіленген. Барлық штрихталған аудан арқылы А ( В С ) жиыны кескінделген. ә) диаграммасында тік сызықтармен А В жиыны, горизонталь сызықтармен А С жиыны белгіленген. Екі рет штрихталған аудан арқылы ( А В ) ( А С ) жиыны кескінделген. Осы кескінделген аудандарды салыстырып, А ( В С ) және ( А В ) ( А С ) жиындарының тең екендігін көреміз.
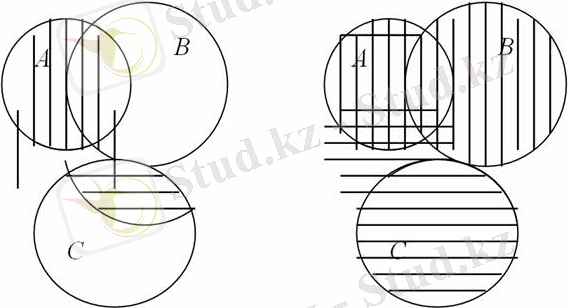
а) ә)
8-сурет
2. 3 ІШКІ ЖИЫНҒА ТОЛЫҚТАУЫШ ЖИЫН. ЖИЫНДАРДЫҢ
АЙЫРМАСЫ. ЕКІ ЖИЫННЫҢ ДЕКАРТТЫҚ КӨБЕЙТІНДІСІ
В
жиыны
А
жиынының ішкі жиыны болсын, яғни
В
А
.
В
жиынында жатпайтын
А
жиынының барлық элементтерінің жиынын
В
-нің толықтауыш жиыны деп атайды.
В
жиынына толықтауыш жиынды
В
 таңбасымен белгілейді. Мысалы
А
1, 2, 3, 4, 5, 6, 7,
В
1, 3, 5, 7 берілсін. Мұндағы
В
А
. Сонда,
В
таңбасымен белгілейді. Мысалы
А
1, 2, 3, 4, 5, 6, 7,
В
1, 3, 5, 7 берілсін. Мұндағы
В
А
. Сонда,
В
 2, 4, 6. Эйлер-Венн диаграммасында
В
2, 4, 6. Эйлер-Венн диаграммасында
В
 жиынына
В
жиынында жатпайтын
А
жиынының барлық нүктелері жатады. 9-сурет.
жиынына
В
жиынында жатпайтын
А
жиынының барлық нүктелері жатады. 9-сурет.
Универсал J жиынының ішкі B жиынының толықтауышы B 1 деп белгіленеді. Мысалы, J - барлық үшбұрыштар жиыны болса, ал B - тік бұрышты үшбұрыштар жиыны болса, онда B 1 - тік бұрышты үшбұрыштардан басқа барлық үшбұрыштар жиыны болады.
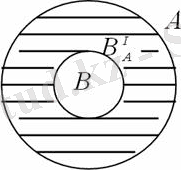
9-сурет
Универсал J жиынының кез-келген A және B ішкі жиындары үшін мына теңдіктер орынды болады:
1) ( А В ) 1 = А 1 В 1 ;
2) ( А В ) 1 = А 1 В 1 .
Бірінші теңдіктің дұрыстығына көз жеткізейік.
х ( А В ) 1 х ( А В ) х А немесе х В х А 1 немесе х В 1 бұдан х ( А 1 В 1 ) . Демек, ( А В ) 1 және А 1 В 1 жиындары бірдей элементтерден тұрады, яғни тең жиындар. Дәл осындай, екінші теңдіктің дұрыстығына да көз жеткізуге болады.
Анықтама. А жиыны мен В жиынының айырмасы деп А жиынының В жиынында жатпайтын элементтерінен тұратын жиынды айтады. А және В жиындарының айырмасы А \ В таңбасымен белгіленеді. Мысалы, A = { a; b; c; d; e }, ал B = { b; c; e; k; m; n }, сонда А \ В = { a; d }, яғни А \ В = А \ ( А В ) . J \ А = А 1 екенін байқаймыз.
Айырманың анықтамасын қысқаша былай жазып көрсетейік: А \ В = { x / x А және х В }.
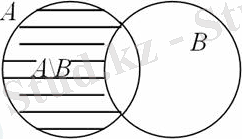
10-сурет
10-суретте А \ В жиыны штрихталған аудан арқылы кескінделген.
Кез келген А , В және С жиындары үшін мына теңдіктер орынды болады:
а) А \ ( В С ) = ( А \ В ) ( А \ С ) ;
ә) А \ ( В С ) = ( А \ В ) ( А \ С ) = ( А \ В ) \ С .
Кортеж ұғымына сүйеніп, екі жиынның декарттық көбейтіндісін анықтауға болады. Ол үшін, шекті екі жиын A = { a; b; c } және В = {3, 5} берілсін. Енді осы жиындардың элементтерінен бірінші компоненті А жиынында, екінші компоненті В жиынында жататын элементтерден тұратын барлық парлардың, яғни ұзындығы 2-ге тең кортеждердің жиынын құрайық. Олар {( а ; 3), ( а ; 5), ( b ; 3), ( b ; 5), ( с ; 3), ( с ; 5) }.
Анықтама. X жиыны мен Y жиынының декарттық көбейтіндісі деп, бірінші компоненті X -ке, екінші компоненті Y -ке жататын элементтерден тұратын барлық парлар жиынын айтады.
Екі жиынның декарттық көбейтіндісін X Y өрнегімен белгілейді. Сонымен X Y = {( x ; у ) / x X, у Y }.
Егер X және Y жиындары тең болса, яғни X = Y , онда X X декарттық көбейтіндісі компоненттері тек X жиынында жататын элементтерден тұратын, x X, у Y, ( х; у ) парлардың жиыны болады. Мысалы, егер X = m; п; p , онда
X X = {( m; m ), ( m; n ), ( m; р ), ( п; m ), ( п; п ), ( п; р ), ( р; m ), ( р; п ), ( р; р ) }.
Сол сияқты, кез-келген X жиыны үшін X = X =.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz