Бигармоникалық функциялар класындағы Риман-Лиувил, Капуто және Адамар-Маршо бөлшек ретті операторларының дифференциалдану қасиеттері


Бигармоникалық функция класындағы бөлшек ретті операторлардың дифференциалдануының кейбір қасиеттері.
1. Кіріспе
Бұл жұмыста бигармониялық функциялар класында анықталған кейбір бөлшек ретті интегро-дифференциалдық операторлардың қасиеттері зерттелінеді.
Айталық,
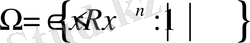 ,
,
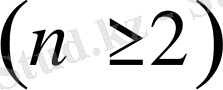 -бірлік шар, ал
-бірлік шар, ал
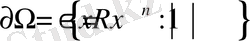 -бірлік сфера. Егер,
-бірлік сфера. Егер,
 шарында
шарында
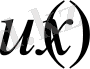 -бигармоникалық функция яғни
-бигармоникалық функция яғни
 және
және
 обласында келесі теңдеу орынды
обласында келесі теңдеу орынды
 ,
,
 .
.
Белгілеу енгіземіз
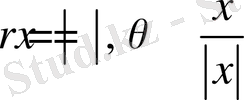 және
және
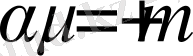 ,
,
 .
.
Келесі операторларды қарастырамыз
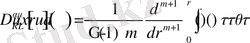 ,
,
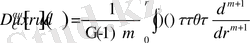 ,
,
мұнда
 -гамма Эйлер функциясы. Мұнда
-гамма Эйлер функциясы. Мұнда
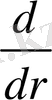 оператор үстінде келесі түрдегі оператор түсініледі
оператор үстінде келесі түрдегі оператор түсініледі
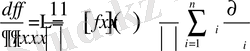 .
.
 -опеераторы Риман-Лиувили мағынасында
-опеераторы Риман-Лиувили мағынасында
 ретті дифференциалдық оператор деп аталады, ал
ретті дифференциалдық оператор деп аталады, ал
 -Капуто мағынасында
-Капуто мағынасында
 ретті дифференциалдық оператор (см.
ретті дифференциалдық оператор (см.
 ) .
) .
Егер
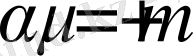 ,
,
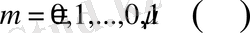 болсын. Қосымша белгілеулер енгіземіз.
болсын. Қосымша белгілеулер енгіземіз.
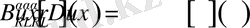 ,
,
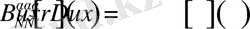 .
.
Бұл оператормен бірге тағы бір түрдегі бөлшек ретті дифференциалдық операторды қарастырамыз, ал егер
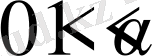
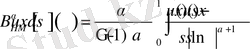 ,
,
Ал егер
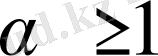 , болса
, болса
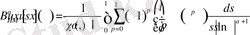 .
.
Мұнда
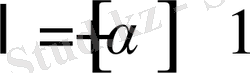 ,
,
 -бүтін бөлігі
-бүтін бөлігі
 ,
,
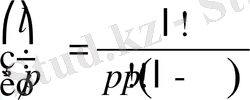 .
.
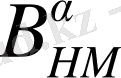 -операторы Адамар-Маршо мағынасында
-операторы Адамар-Маршо мағынасында
 ретті дифференциалдық оператор деп аталады. (см.
ретті дифференциалдық оператор деп аталады. (см.
 )
)
2. Риман-Лиувил және Капуто мағынасындағы бөлшек ретті дифференциалдық оператор қасиеттері.
1-Лемма.
Егер
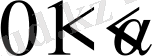 және
және
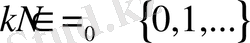 дәрежелі
дәрежелі
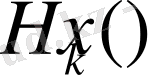 -біртекті гармоникалық полином болсын.
-біртекті гармоникалық полином болсын.
Онда теңдік дұрыс
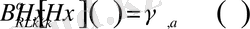 (1)
(1)
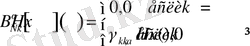 (2)
(2)
мұнда
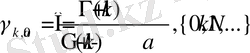 .
.
Бұл лемманың дәлелдеуі
 жұмыста көрсетілген. Дәл сондай келесі лемма дәлелденеді.
жұмыста көрсетілген. Дәл сондай келесі лемма дәлелденеді.
2-Лемма.
Егер
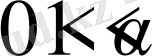 және
және
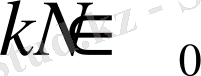 дәрежелі
дәрежелі
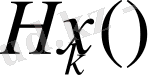 -біртекті гармоникалық полином болсын, онда келесі теңдік дұрыс
-біртекті гармоникалық полином болсын, онда келесі теңдік дұрыс
 (3)
(3)
3-Лемма.
Егер
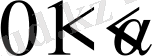 ,
,
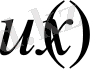 функция
функция
 шарында бигармоникалық болсын, онда кез-келген
шарында бигармоникалық болсын, онда кез-келген
 үшін келесі теңдік орынды
үшін келесі теңдік орынды
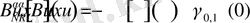 (4)
(4)
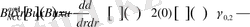 (5)
(5)
Дәлелдеу.
Белгілеу бойынша
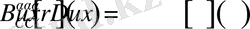 тең.
тең.
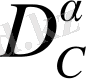 оператор анықтамасын қолданып келесіні аламыз
оператор анықтамасын қолданып келесіні аламыз

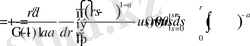


(4) теңдік дәлелденді.
Енді екінші лемма теңдігіне өтеміз. Анықтама бойынша
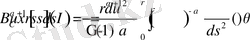
Ең сонғы интегралды келесі түрде болады
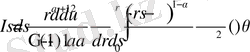
және бөліктеп интегралдап келесіні аламыз
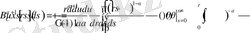

Сонғы интегралды зерттеп
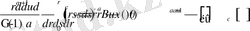

Сондықтан
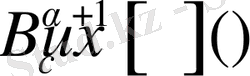 үшін (5) теңдік дұрыс. Лемма дәлелденді.
үшін (5) теңдік дұрыс. Лемма дәлелденді.
(4) және (5) теңдіктен келесіні аламыз.
1-Салдар.
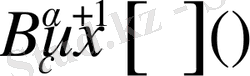 үшін келесі теңдік орынды
үшін келесі теңдік орынды
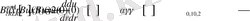 (6)
(6)
1-Теорема.
Егер
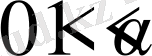 ,
,
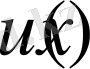 функция
функция
 обласында бигармоникалық болса, онда
обласында бигармоникалық болса, онда
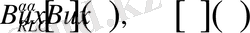 функцияларыда
функцияларыда
 обласында бигармоникалық функция болады және
обласында бигармоникалық функция болады және
 теңдікке тең.
теңдікке тең.
Дәлелдеу.
Егер
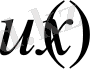 функция
функция
 обласында бигармоникалық болса, онда Альманси теоремасыдан
обласында бигармоникалық болса, онда Альманси теоремасыдан
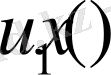 және
және
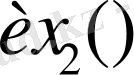 функциялары
функциялары
 обласында гармоникалық болады, сондықтан
обласында гармоникалық болады, сондықтан
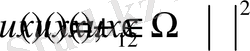
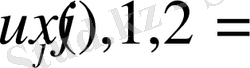 гармоникалық функцияларды қатар түрінде көрсетеміз
гармоникалық функцияларды қатар түрінде көрсетеміз
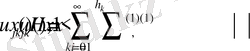 , (7)
, (7)
ал
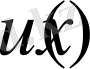 үшін
үшін
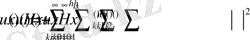 (8)
(8)
Мұнда
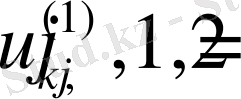 (8) есептің жіктелу коэффийенттері, ал
(8) есептің жіктелу коэффийенттері, ал
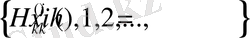 k дәрежелі біртекті гармоникалық полиномдардың толық системасы.
k дәрежелі біртекті гармоникалық полиномдардың толық системасы.
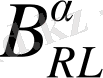 операторыны (8) - қатарға қолданып
операторыны (8) - қатарға қолданып
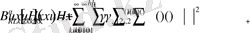 (9)
(9)
аламыз
(9) теңдіктің оң жағынан алынған қатар обсалютті жинақы және
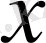 боыйынша
боыйынша
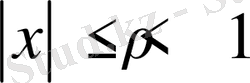 бір қалыпты жинақы және олардың қосындысы гармоникалық функцияларды көрсетеді. Ол функцияларды
бір қалыпты жинақы және олардың қосындысы гармоникалық функцияларды көрсетеді. Ол функцияларды
 және
және
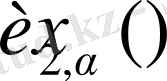 арқылы белгілейміз. Онда
арқылы белгілейміз. Онда
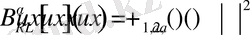 .
.
Бұл теңдеуден Альманси теоремасы бойынша
 обласында
обласында
 бигармоникалық функция.
бигармоникалық функция.
 функция (4) формула бойынша
функция (4) формула бойынша
 функциясы арқылы белгілейміз, сондықтан онда
функциясы арқылы белгілейміз, сондықтан онда
 обласында бигармоникалық болады.
обласында бигармоникалық болады.
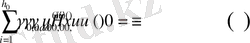 , (4) теңдіктен
, (4) теңдіктен
 .
.
Теорема дәлелденді.
4-Лемма.
Егер k дәрежелі
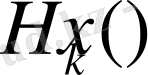 -біртекті гармоникалық полином болса,
-біртекті гармоникалық полином болса,
Онда келесі теңдік орынды
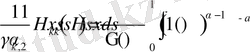 , (10)
, (10)
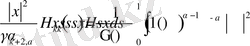 (11)
(11)
Дәлелдеу.
Егер k дәрежелі
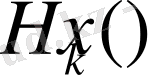 -біртекті гармоникалық полином болса, онда
-біртекті гармоникалық полином болса, онда
 біртектілікті қолданып
біртектілікті қолданып

сәйкесінше,
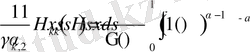 .
.
(10) -теңдік дәлелденді.
және (11) -дәлелдеуден

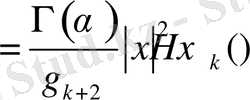
Мұнда
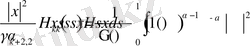
(11) -теңдік және лемма дәлелденді.
2-Теорема.
Егер
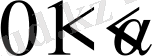 және
және
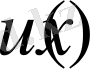 функция
функция
 обласында бигармоникалық болса, онда кез келген
обласында бигармоникалық болса, онда кез келген
 үшін келесі теңдік дұрыс
үшін келесі теңдік дұрыс
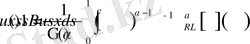 (12)
(12)
Дәлелдеу.
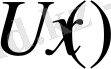 бигармоникалық функция қатар түрінде аламыз
бигармоникалық функция қатар түрінде аламыз
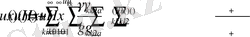
(10) және (11) теңдіктері және қатардың бір қалыпты жинақтылығынан келесі теңдік орынды
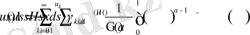
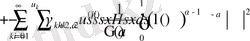

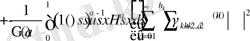 .
.
Ең сонғы өрнекте келесі түрлендіру жасаймыз
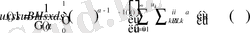
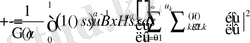

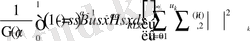

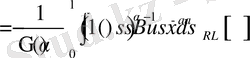 .
.
Сондықтан,
 .
.
Теорема дәлелденді.
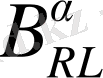 және
және
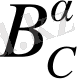 операторлардың байланысыдан келесі тұжырым шығады.
операторлардың байланысыдан келесі тұжырым шығады.
3-Теорема.
Егер
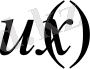 функция
функция
 обласында бигармоникалық болса, онда кез келген
обласында бигармоникалық болса, онда кез келген
 үшін келесі теңдік дұрыс
үшін келесі теңдік дұрыс
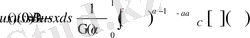 (13)
(13)
Дәлелдеу.
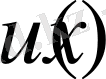 функция үшін 2-Теоремадағы тұжырымдың көмегімен (12) теңдік дұрыс. (4) теңдікті қолданып
функция үшін 2-Теоремадағы тұжырымдың көмегімен (12) теңдік дұрыс. (4) теңдікті қолданып

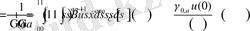

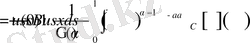 .
.
Теорема дәлелденді.
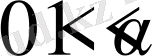 бигармоникалық функция класында болған (12) көмегімен келесі операторды анықтауға болады
бигармоникалық функция класында болған (12) көмегімен келесі операторды анықтауға болады
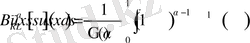 ,
,
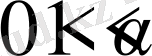 .
.
4-Теорема.
Егер
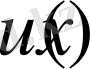 функция
функция
 обласында бигармоникалық болса онда
обласында бигармоникалық болса онда
 функциясыда
функциясыда
 обласында бигармоникалық болады.
обласында бигармоникалық болады.
Дәлелдеу.
 шарында теңдік дұрыс екенін табамыз
шарында теңдік дұрыс екенін табамыз
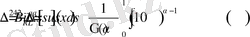
Теорема дәлелденді.
5-Теорема.
Егер
 функция
функция
 обласында бигармоникалық болса, онда келесі теңдік дұрыс
обласында бигармоникалық болса, онда келесі теңдік дұрыс
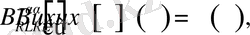
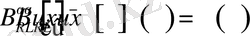 (14)
(14)
Дәлелдеу.
(14) тің бірінші теңдігін дәлелдейміз.
 функциясын
функциясын
 оперторды қолданамыз.
оперторды қолданамыз.
 опертор анықтамасы бойынша және
опертор анықтамасы бойынша және
2-Теоремаға байланысты келесіні аламыз
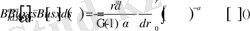

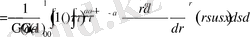 .
.
Келесі теңдік дұрыс екеніне көз жеткізуге болады

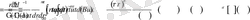
Мұнда
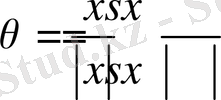 және (12) теңдікті қолданып келесіні аламыз
және (12) теңдікті қолданып келесіні аламыз
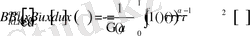
Теорема дәлелденді.
2-Салдар.
Егер
 функция
функция
 обласында бигармоникалық болса, онда келесі теңдік дұрыс
обласында бигармоникалық болса, онда келесі теңдік дұрыс
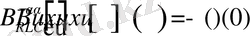
Дәлелдеу. (4) теңдікті қолданып
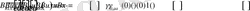
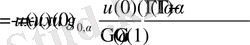
Салдар дәлелденді.
3. Адамар-Маршо дифференциалдық опереторының қасиеттері.
Ендеше
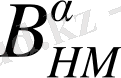 операторымен бірге келесі оператор қарастырамыз
операторымен бірге келесі оператор қарастырамыз
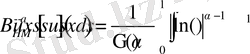
5-Лемма.
Егер
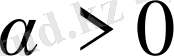 және
және
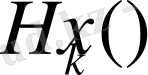 біртекті
біртекті
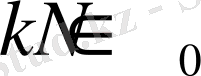 дәрежелі гармоникалық полином болсын. Онда келесі теңдік дұрыс екеніне көз жеткізуге болады
дәрежелі гармоникалық полином болсын. Онда келесі теңдік дұрыс екеніне көз жеткізуге болады
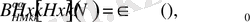 , (15)
, (15)
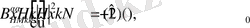 , (16)
, (16)
Дәлелдеу. Теңдіктер бірдей дәлелденетін болғандықтан лемманың екінші теңдігінің дәлелдеуін көрсетеміз
Егер
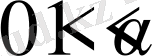 болса, онда
болса, онда
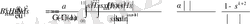

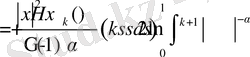 .
.
Сонғы интегралды шешеміз. Айнымалылардың орын алмастырудан
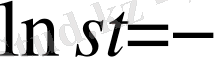 интегралы келесі түрде болады
интегралы келесі түрде болады

сондықтан
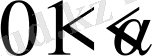 болғанда
болғанда
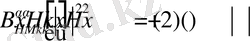 .
.
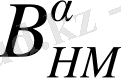 оператор әсері
оператор әсері
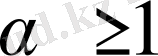 болғанда
болғанда
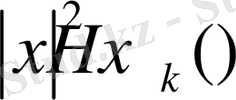 функциясы үшін дәл сондай тексеріледі. Лемма дәлелденді.
функциясы үшін дәл сондай тексеріледі. Лемма дәлелденді.
6-
Лемма.
Егер
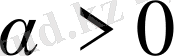 және
және
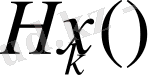 -біртекті k дәрежелі гармоникалық полином болсын, онда теңдік дұрыс
-біртекті k дәрежелі гармоникалық полином болсын, онда теңдік дұрыс
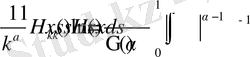 , (17)
, (17)
 . (18)
. (18)
Дәлелдеу.
Егер
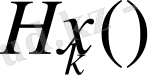 -біртекті
-біртекті
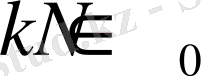 дәрежелі гармоникалық полином болса, онда
дәрежелі гармоникалық полином болса, онда
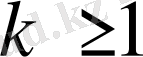 болғанда
болғанда

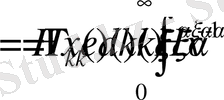
Дәл сондай келесі интеграл шешеміз

яғни
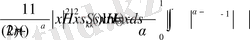
Лемма дәлелденді.
6-Теорема. Егер
және
функция
обласында бигармоникалық болса, онда
функциясыда
обласында бигармоникалық болады және
 .
.
Дәлелдеу.
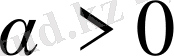 және
және
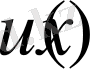 функциясы
функциясы
 обласында бигармоникалық функция болсын.
обласында бигармоникалық функция болсын.
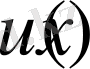 ті (8) теңдік түрінде көрсетіп және оған
ті (8) теңдік түрінде көрсетіп және оған
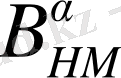 операторды қолданамыз, (15) және (16) теңдіктерін қолданып
операторды қолданамыз, (15) және (16) теңдіктерін қолданып
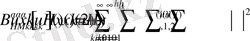 (19)
(19)
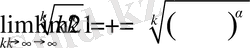 болса, онда сонғы қатар абсалютты жинақты және x бойынша бір қалыпты
болса, онда сонғы қатар абсалютты жинақты және x бойынша бір қалыпты
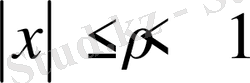 және оның қосынды
және оның қосынды
 обласында бигармоникалық функция болады.
обласында бигармоникалық функция болады.
(19) теңдікте бос мүше жоқ және сондықтан
 тең. Теорема дәлелденді.
тең. Теорема дәлелденді.
7-Теорема. Егер
және
функция
обласында бигармоникалық болса, онда
обласының кез келген
нүктесінде
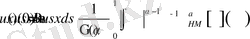 (13)
(13)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz