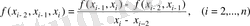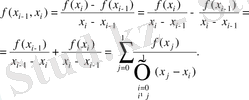Сандық талдаудың негіздері: абсолюттік және салыстырмалы қателер, интерполяция және сызықтық теңдеу жүйелерін шешу әдістері


Абсолюттік және салыстырмалы қателер
Есептеу кезінде қолданылатын
 санынан аз ғана айрмашылығы бар
санынан аз ғана айрмашылығы бар
 санын жуық сан дейміз. Егер
санын жуық сан дейміз. Егер
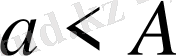 болса,
болса,
 санын кемітіліп алынған, ал
санын кемітіліп алынған, ал
 болса, онда артығымен алынған
болса, онда артығымен алынған
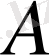 санының мәні дейді.
санының мәні дейді.
Жуықтап алынған а санының қатесі деп
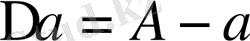 өрнегін айтамыз. Егер
өрнегін айтамыз. Егер
 болса, онда
болса, онда
 ал
ал
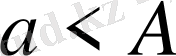 болса, онда
болса, онда
 Көп жағдайда
Көп жағдайда
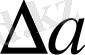 ның таңбасы белгісіз болады. Сондықтан көбінесе
ның таңбасы белгісіз болады. Сондықтан көбінесе
 -
-
 абсолюттік қате қолданылады. Яғни
абсолюттік қате қолданылады. Яғни
. (1. 1)
Егер
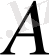 саны бізге белгісіз болса, онда (1. 1) формула арқылы абсолюттік қатені анықтау мүмкін емес. Мұндай жағдайда
саны бізге белгісіз болса, онда (1. 1) формула арқылы абсолюттік қатені анықтау мүмкін емес. Мұндай жағдайда
 ның жоғарғы шегі-
ның жоғарғы шегі-
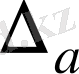 ны анықтайды.
ны анықтайды.
. (1. 2)
 -ны шектік абсолюттік қате деп атайды. (1. 2) формуладан мына формуланы аламыз.
-ны шектік абсолюттік қате деп атайды. (1. 2) формуладан мына формуланы аламыз.
(1. 3)
 санын
санын
 санының кемітілген жуық мәні, ал
санының кемітілген жуық мәні, ал
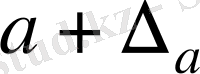 санын арттырылған жуық мәні дейді. Мұндайда
санын арттырылған жуық мәні дейді. Мұндайда
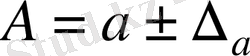 жазуын қолданады.
жазуын қолданады.
Абсолюттік қате, көп жағдайларда есептеу кезінде немесе өлшеу кезінде жіберілген қатені дәл сипаттай алмайды.
Өлшеудің сапасын анықтау үшін салыстырмалы қатені қолданады. Ол былайша табылады:
. (1. 4)
Ал
 болса, онда
болса, онда
 шектік салыстырмалы қате делінеді. Шектік салыстырмалы қате ретінде
шектік салыстырмалы қате делінеді. Шектік салыстырмалы қате ретінде
(1. 5)
санын алуға болады. Егер
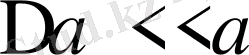 және
және
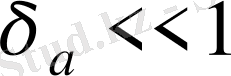 болса, онда абсолюттік қате мен салыстырмалы қатені былайша жуықтап алуға болады:
болса, онда абсолюттік қате мен салыстырмалы қатені былайша жуықтап алуға болады:
(1. 6)
(1. 7)
Лекция 2. Арифметикалық амалдарды қолданған кездегі қателер.
Жуықтап алынған сандарға қосу, азайту, көбейту, бөлу амалдарын пайдаланғанда түпкілікті қателер қалайша өзгеретінін қарастырайық.
1. Қосу және азайту.
- санының дәл мәндерінің қосындысы болсын, ал
- сандардың жуық мәндерінің қосындысы делік. Сонда
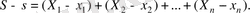
Осыдан
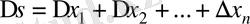 немеcе
немеcе
. (2. 1)
(2. 1) теңсіздігі жуық сандардың қосындысының абсолюттік қатесі қосылғыштардың абсолюттік қателерінің қосындысынан үлкен болмайтынын көрсетеді.
сандары ретімен
сандарының шектік абсолюттік қатесі болсын. Сонда
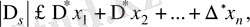
немесе
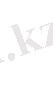
(2. 2)
Сандардың айырымдары үшін де (2. 2) формула дұрыс.
Әртүрлі абсолюттік дәлдіктегі сандарды қосқанда есептеуді былай жүргізген жөн:
- Ең үлкен абсолюттік қатесі бар санды бөліп аламыз.
- Дәлірек сандардың бөліп алған санға қарағанда бір цифрлік мәнін артық қалдырып қалғанын дөңгелектейміз.
- Қосу амалын қолданғанда санның барлық цифрлік мәндерін сақтаймыз.
- Қосындының соңғы цифрлік мәнін дөңгелектейміз.
Енді сандардың қосындысының шектік салыстырмалы қатесін қарастырайық.
Бізге
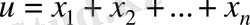 берілсін және
берілсін және
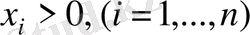 болсын.
болсын.
 дің дәл мәні дейік, ал
дің дәл мәні дейік, ал

Сонда шектік салыстырмалы қатені былайша алуға болады.
(2. 3)
Немесе
, (2. 4)
себебі
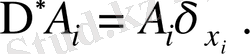
 салыстырмалы қателер-
салыстырмалы қателер-
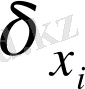 дің ең үлкен мәні болсын дейік
дің ең үлкен мәні болсын дейік
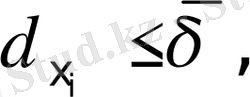 сонда
сонда
демек
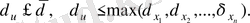
Егер
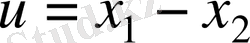 болса, онда
болса, онда
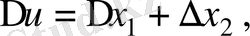 . (2. 5)
. (2. 5)
Сондықтан
(2. 6)
мұнда
 мен
мен
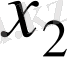 нің айрымының абсолюттік дәл мәні.
нің айрымының абсолюттік дәл мәні.
(2. 6) формуладан өте жақын сандарды бір-бірінен алғанда дәлдікті жоғалтып алу қаупі бар екенін көреміз. Сондықтан, мұндай жағдайда оларды түрлендіру арқылы есептеген дұрыс.
Мысалы:
а
мен
b
саны бір-біріне өте жақын болған жағдайда
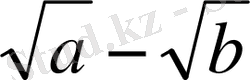 өрнегін есептегеннен
өрнегін есептегеннен
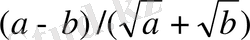 өрнегін есептеген дәлірек.
өрнегін есептеген дәлірек.
2. Көбейту.
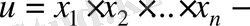 жуықтап алынған сандардың көбейтіндісі және
жуықтап алынған сандардың көбейтіндісі және
 болсын.
болсын.
Сонда
(2. 7)
 формуласын пайдалана отырып (2. 7) теңдіктен
формуласын пайдалана отырып (2. 7) теңдіктен
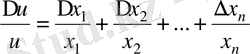 теңдікті аламыз.
теңдікті аламыз.
Соңғы өрнектен төмендегідей теңсіздікті аламыз,
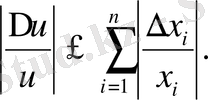
Егер
 санының дәл мәні және
санының дәл мәні және
 болса, онда
болса, онда
және
,
мұнда
 санының салыстырмалы қатесі, ал
санының салыстырмалы қатесі, ал
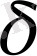 - көбейтіндінің салыстырмалы қатесі.
- көбейтіндінің салыстырмалы қатесі.
Сондықтан
. (2. 8)
(2. 8) формуласы
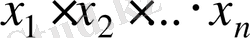 сандарының таңбалары әртүрлі болған жағдайда да орындалатыны айқын. Ал
сандарының таңбалары әртүрлі болған жағдайда да орындалатыны айқын. Ал
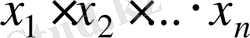 сандарының көбейтіндісінің шектік салыстырмалы қатесі -
сандарының көбейтіндісінің шектік салыстырмалы қатесі -
(2. 9)
ал шектік абсолюттік қате -
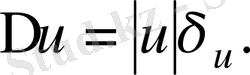
3. Бөлу. Егер
 болса, онда
болса, онда
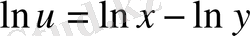 және
және
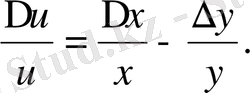
Осыдан
. (2. 10)
Сонымен бөлу амалын қолданғанда жіберілген қателер мен көбейту амалдарында жіберілген қателер (2. 8), (2. 10) формулалары арқылы аңықталатындығын көреміз.
4. Дәрежелеу.
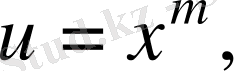 (m-натурал сан) болсын, онда
(m-натурал сан) болсын, онда
, сондықтан

Осыдан
. (2. 11)
Түбір табу.
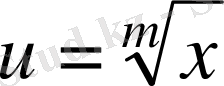 болсын, сонда
болсын, сонда
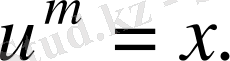 Осыдан
Осыдан
(2. 12)
Дәрежелеу мен түбір тапқанда
 функциясы жіберетін қатені жалпы былай жазуға болады:
функциясы жіберетін қатені жалпы былай жазуға болады:
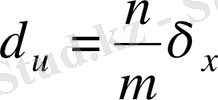 . (2. 13)
. (2. 13)
Лекция 3. Интерполяциялау есебінің қойылуы .
Техникада, физикада, экономикада т. с. жаратылыс тану ғылымдарында функцияның мәні таблица түрінде беріледі. Мысалы
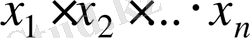 нүктелерінде функцияның мәндері-
нүктелерінде функцияның мәндері-
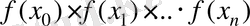 беріледі. Таблица арқылы берілген функцияның кемшілігі- оның кез-келген, таблицада көрсетілмеген, нүктедегі мәнінің белгісіздігі.
беріледі. Таблица арқылы берілген функцияның кемшілігі- оның кез-келген, таблицада көрсетілмеген, нүктедегі мәнінің белгісіздігі.
Көп жағдайда аналитикалық жолмен берілген
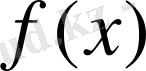 функциясының мәнін есептеу өте күрделі, немесе таблица арқылы берілген функцияның мәндері өте қымбатқа түсетін эксперименттер арқылы алынған болса, онда
функциясының мәнін есептеу өте күрделі, немесе таблица арқылы берілген функцияның мәндері өте қымбатқа түсетін эксперименттер арқылы алынған болса, онда
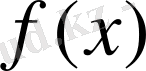 функциясын, мәні оңай есептелінетін, қарапайым
функциясын, мәні оңай есептелінетін, қарапайым
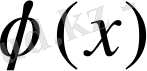 функциясымен алмастырған тиімдірек болады. Қысқаша айтқанда функцияның аргументінің кез-келген мәнінде, белгілі бір мағынада,
функциясымен алмастырған тиімдірек болады. Қысқаша айтқанда функцияның аргументінің кез-келген мәнінде, белгілі бір мағынада,
 болуы керек. Осы
болуы керек. Осы
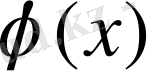 функциясын табудың мәселелерін- интерполяциялау теориясы дейміз.
функциясын табудың мәселелерін- интерполяциялау теориясы дейміз.
Енді осы интерполяциялау теориясының ең қарапайым түрін қарастырайық.
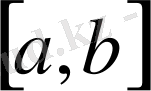 кесіндісінде жататын
кесіндісінде жататын
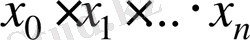 нүктелері және осы нүктелердегі
нүктелері және осы нүктелердегі
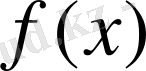 функциясының мәндері-
функциясының мәндері-
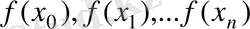 берілген.
берілген.
 болатындай
болатындай
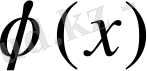 функциясын (интерполяциялаушы функция) табу керек.
функциясын (интерполяциялаушы функция) табу керек.
Мұның геометриялық мағынасы:
нүктелерінен өтетін
сызығын табу керек деген сөз.

1-сурет
Есептің бұл қойылымында көптеген шешулер болуы, немесе болмауы да мүмкін. Алайда кез-келген
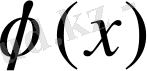 функцияның орнына дәрежесі n-нен үлкен емес,
P
n
(x
і
) =f(x
і
) (і=0, . . . , n)
теңдігін қанағаттандыратын
P
n
(x)
алгебралық көпмүшелігін алатын болсақ, онда есептің шешуі біреу ғана болады.
P
n
(x)
көпмүшелігін-интерполяциялық көпмүше дейді.
функцияның орнына дәрежесі n-нен үлкен емес,
P
n
(x
і
) =f(x
і
) (і=0, . . . , n)
теңдігін қанағаттандыратын
P
n
(x)
алгебралық көпмүшелігін алатын болсақ, онда есептің шешуі біреу ғана болады.
P
n
(x)
көпмүшелігін-интерполяциялық көпмүше дейді.
Егер
x
0
<x
1
< . . . <x
n
, ал
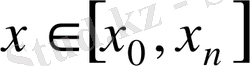 болса, онда
болса, онда
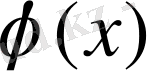 функциясының мәні, тар мағанада интерполяциялау,
функциясының мәні, тар мағанада интерполяциялау,
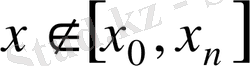 болса, экстрополяциялау арқылы табылады дейді. Алдағы уақытта жалпы
болса, экстрополяциялау арқылы табылады дейді. Алдағы уақытта жалпы
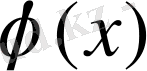 функциясын табуды- интерполяциялау дейміз.
функциясын табуды- интерполяциялау дейміз.
Лагранждың интерполяциялау формуласы .
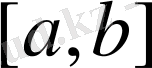 кесіндісінде жататын
кесіндісінде жататын
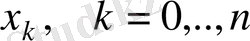 нүктелері және осы нүктелерде
нүктелері және осы нүктелерде
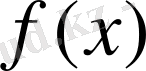 функциясының мәндері-
функциясының мәндері-
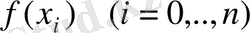 берілген. Осы функцияны интерполяциялау үшін n дәрежелі алгебралық көпмүшені
берілген. Осы функцияны интерполяциялау үшін n дәрежелі алгебралық көпмүшені
(2. 1)
қолданамыз. Мұндағы
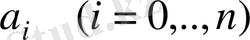 коэффициенттерін
коэффициенттерін
болатындай етіп табу керек.
Кез-келген үзіліссіз
 функциясы үшін бұл есептің шешімі біреу ғана болады. Себебі
функциясы үшін бұл есептің шешімі біреу ғана болады. Себебі
(2. 2)
теңдеулер жүйесінің аңықтауышы нольден айырықша (Вандермонд аңықтауышы) .
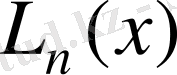 көпмүшесін,
көпмүшесін,
 нүктелері бойынша тұрғызылған,
нүктелері бойынша тұрғызылған,
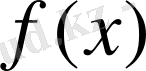 функциясын интерполяциялаушы көпмүше дейміз.
функциясын интерполяциялаушы көпмүше дейміз.
(2. 2) теңдеулер жүйесінің шешімдерін әртүрлі жолмен табуға болады. Оның көп қолданатын түрлері Лагранж бен Ньютонның интерполяциялық көпмүшеліктері.
Лагранждың интерполяциялық көпмүшелігін
(2. 3)
түрінде қарастырамыз. (2. 2) шартын ескере отырып,
(2. 4)
теңдігін аламыз. Егер
(2. 5)
болса, онда (2. 4) шарты орындалады.
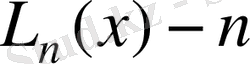 дәрежелі көпмүше болғандықтан
дәрежелі көпмүше болғандықтан
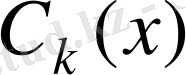 коэффициентін де n дәрежелі көпмүше ретінде іздеген дұрыс. Атап айтқанда
коэффициентін де n дәрежелі көпмүше ретінде іздеген дұрыс. Атап айтқанда
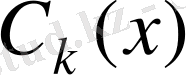 көпмүшесін
көпмүшесін
(2. 6)
түрінде іздейміз.
 шартың ескере отырып, (2. 6) формуладан
шартың ескере отырып, (2. 6) формуладан
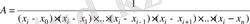
және
(2. 7)
формуласын табамыз. Сонымен Лагранж көпмүшесі толық былайша жазылады.
. (2. 8)
Егер
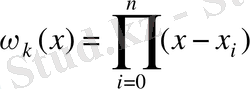 десек, онда
десек, онда

ал
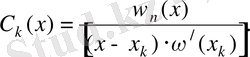
Сондықтан Лагранж көпмүшесін былайша ықшамдап жазуға болады:
(2. 9)
Енді интерполяциялық Лагранж көпмүшесінің жіберетін қатесін қарастырайық.
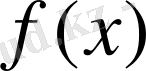 функциясын
функциясын
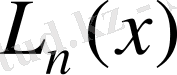 көпмүшесімен алмастырғанда жіберетін қатеміз
көпмүшесімен алмастырғанда жіберетін қатеміз
(2. 10)
Кейде
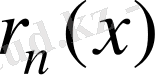 функциясын Лагранж көпмүшесінің қалдығы деп те атайды.
функциясын Лагранж көпмүшесінің қалдығы деп те атайды.
Кез-келген
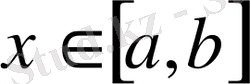 нүктесіндегі қалдықты табу үшін мына көмекші функцияны қарастырамыз:
нүктесіндегі қалдықты табу үшін мына көмекші функцияны қарастырамыз:
, (2. 11)
мұнда
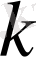 -тұрақты сан.
-тұрақты сан.
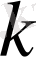 санын
санын
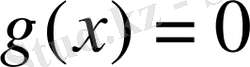 болатындай, яғни
болатындай, яғни
(2. 12)
деп алсақ, онда
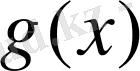 ең болмағанда
ең болмағанда
 нүктеде нольге тең болады.
нүктеде нольге тең болады.
Енді
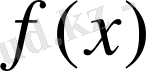 функциясының
функциясының
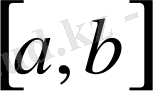 кесіндісінде үзіліссіз
кесіндісінде үзіліссіз
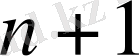 ретті туындысы бар болсын. Сонда
ретті туындысы бар болсын. Сонда
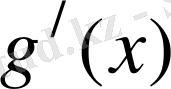 , Роль теоремасы бойынша,
, Роль теоремасы бойынша,
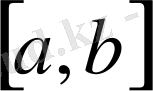 кесіндісінде ең болмағанда n+1 нүктеде нөлге тең, ал
кесіндісінде ең болмағанда n+1 нүктеде нөлге тең, ал
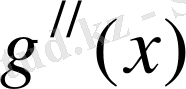 -ењ, болмағанда n нүктеде нөлге тең, т. с.
-ењ, болмағанда n нүктеде нөлге тең, т. с.
 ең болмағанда бір нүктеде нөлге тең болады. Сонымен
ең болмағанда бір нүктеде нөлге тең болады. Сонымен
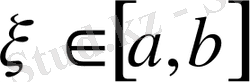 табылады да
табылады да
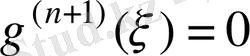 болады.
болады.
Ал
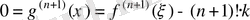 болғандықтан
болғандықтан
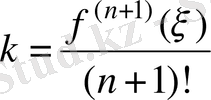 . (2. 13)
. (2. 13)
(2. 12) және (2. 13) формулаларды ескере отырып,
(2. 14)
формуласын аламыз.
Осыдан
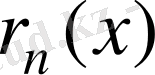 функциясын жоғарыдан бағалау арқылы
функциясын жоғарыдан бағалау арқылы
. (2. 15)
теңсіздігін аламыз, мұндағы
 .
.
Егер
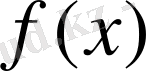 дәрежесі n-нен үлкен емес көпмүше болса, онда
дәрежесі n-нен үлкен емес көпмүше болса, онда
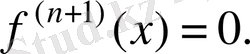
Сондықтан
.
Лекция 4. Бөлінген айырымдар және Ньютон формуласы .
Бізге
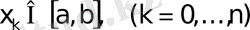 нүктелерінде
нүктелерінде
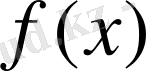 функциясының мәндері берілген және
функциясының мәндері берілген және
 деп ұйғрасақ. Нольдік ретті бөлінген айырымдар деп
деп ұйғрасақ. Нольдік ретті бөлінген айырымдар деп
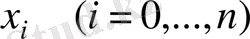 нүктелеріндегі
нүктелеріндегі
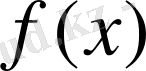 функциясының мәні-
функциясының мәні-
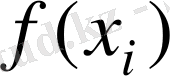 -ді айтамыз. Бір ретті бөлінген айырым деп
-ді айтамыз. Бір ретті бөлінген айырым деп
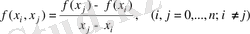
өрнектерін айтамыз. Бір ретті бөлінген айырымдар арқылы екі ретті бөлінген айырымдарды алуға болады:
Егер k-ретті бөлінген айырымдар
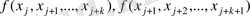 белгілі болса, онда
k+1
- ретті бөлінген айырым былайша табылады:
белгілі болса, онда
k+1
- ретті бөлінген айырым былайша табылады:
.
k -ретті бөлінген айырымды былайда табуға болады:
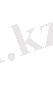
 . (3. 1)
. (3. 1)
(3. 1) формуласының дұрыстығын математикалық индукция арқылы дәлелдеуге болады.
Егер
k=0
болса, онда
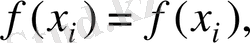 ал
k=1
болса, онда
ал
k=1
болса, онда
Енді (3. 1) формуласы
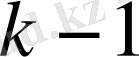 ретті бөлінген айырымдар үшін дұрыс деп алып,
ретті бөлінген айырымдар үшін дұрыс деп алып,
 ретті бөлінген айырымдар үшін де дұрыс екенін көрсетейік:
ретті бөлінген айырымдар үшін де дұрыс екенін көрсетейік:
(3. 2)
Бұл өрнекте
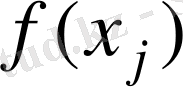 және
және
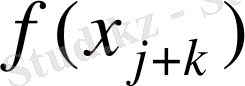 бірден ғана кездеседі, ал қалған
бірден ғана кездеседі, ал қалған
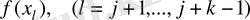 квадрат жақшаның ішіндегі қосындылардың екеуінде де кездеседі. Оларды бір-біріне қосу арқылы (3. 1) формуласын аламыз. Бізге бұл формуланың, алдағы уақытта, дербес түрі
квадрат жақшаның ішіндегі қосындылардың екеуінде де кездеседі. Оларды бір-біріне қосу арқылы (3. 1) формуласын аламыз. Бізге бұл формуланың, алдағы уақытта, дербес түрі
(3. 3)
керек болады.
Енді Лагранж көпмүшелігі-
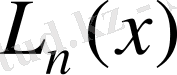 функциясын былайша жазайық.
функциясын былайша жазайық.
(3. 4)
Интерполяцияның (2. 4) шарты бойынша
Сондықтан
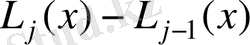 j-дәрежелі,
j-дәрежелі,
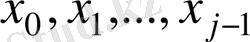 нүктелерінде нөлге тең, алгебралық көпмүшелік болады, яғни
нүктелерінде нөлге тең, алгебралық көпмүшелік болады, яғни
(3. 5)
мұндағы
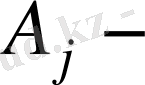 сандық коэффициент.
сандық коэффициент.
Бұл коэффициент мына теңдіктен табылады:
. (3. 6)
Осыдан
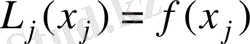 екенін ескере отырып,
екенін ескере отырып,
(3. 7)
формуласын аламыз.
Енді
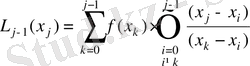
екенін ескерсек, онда
 (3. 8)
(3. 8)
(3. 8) формуласын (3. 3) формуласымен салыстыра отырып,
(3. 9)
екенін көреміз.
Осыдан (3. 4), (3. 5), (3. 9) формулаларын ескере отырып,
(3. 10)
формуласын аламыз. (3. 10) түрінде жазылған Лагранж көпмүшесін Ньютон интерполяциялық формуласы дейміз. Алдағы уақытта оны
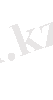
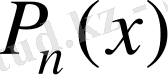 деп белгілейміз. Біз Ньютон формуласының қалдығы Лагранж формуласының қалдығымен бірдей екенін білеміз. Енді Ньютон формуласының қалдығын басқа түрде жазайық.
деп белгілейміз. Біз Ньютон формуласының қалдығы Лагранж формуласының қалдығымен бірдей екенін білеміз. Енді Ньютон формуласының қалдығын басқа түрде жазайық.
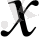 нүктесі
нүктесі
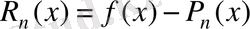 қалдығының шамасын қарастыратын нүкте болсын.
қалдығының шамасын қарастыратын нүкте болсын.
Онда

теңдігінен
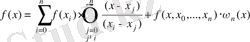
формуласын аламыз.
Осыдан
(3. 11)
(2. 14), (3. 11) формулаларын салыстыра отырып,
нүктесі табылып, және сол нүктеде
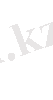

(3. 12)
теңдігі орындалатынын көреміз.
(3. 12) формуласы функцияның
ретті туныдысы мен
ретті бөлінген айырымының арақатынасын көрсетеді.
Лекция 5 -Лекция 6. Сызықтық теңдеулер жүйесін шешу әдістері
Теңдеулер жүйелерін шешу жолдары әдетте, дәл және итерациялық әдістер болып екі топқа бөлінеді.
Дәл әдістер орындалатын арифметикалық амалдар саны санаулы болатын өрнектерден тұрады. Теңдеулер жүйесін шешу үшін қолданылатын Крамер, Гаусс, қуалау әдістері осы топқа жатады. Жүйені анықтайтын деректер дәл берілгенде және есептеулер дәл орындалғанда, олар жүйенің дәл шешімін беруі тиіс.
Итерациялық әдістер бір немесе бірнеше параметрлері үнемі өзгеріп тұратын алгебралық біртекті өрнектерден құралады. Олар жүйенің жуық шешімін векторлар тізбегінің шегі ретінде анықтайды. Тізбектелген алгебралық өрнектерді итерациялық әдістің есептеу алгоритмі деп атайды.
Енді жоғарыда аталған мәселелерге жеке-жеке тоқталайық.
1. Векторлар мен матрицалардың нормалары және олардың негізгі қасиеттері.
Векторлардың нормалары. R n векторлық кеңістікте
векторы берілсін. Мұндағы х і -вектордың і-координаты.
Анықтама. Х векторының нормасы-X деп мна шарттарды қанағаттандыратын теріс емес санды айтамыз:
- X >0егерболса жәнеX=0егерХ=0болса;
- cX=c X, с-кез-келген сан;
3) X+У < X+У (үшбұрыш теңсіздігі) .
Соңғы екі шарттан мына теңсіздікті алуға болады
X-У > X-У .
Шынында да X =X+У-У < X-У+У.
Осыдан X - У <X-У .
Сызықтық алгебрада вектордың төмендегі үш нормасы жиі қолданылады:
1)
(кубтық норма) ; (1. 1)
2)
(октаэдрлік норма) ; (1. 2)
3)
(сфералық норма) ; (1. 3)
Соңгы норманы вектордың ұзындығы дейді. Бұл үш нормада анықтаманың үш шартын да қанағаттандырады. Бірінші және екінші шарттардың орындалуы айқын болғандықтан, бұлар үшінші шартты да қанағаттандыратының көрсетейік.
Бірінші және екінші нормалар үшін мына теңсіздіктер орындалады:
;
;
Ал үшінші норма үшін Коши-Буняковский теңсіздігін пайдалансақ:
Осыдан
.
Егер
,
оң нақты сандары үшін векторлардың нормалары
,
мына шартты қанғаттандырса
, онда оларды эквивалентті нормалар дейді. Жоғарыда көрсетілген нормалар өзара эквивалентті. өйткені олар мына теңсіздіктерді қанағаттандырады.
(1. 4)
(1. 5)
(1. 6)
(1. 4), (1. 5) теңсіздіктері мен (1. 6) теңсіздігінің оң жағы айқын болғандықтан, біз (1. 6) теңсіздігінің сол жағын дәлелдесек болғаны. Шынында да
.
Осыдан
.
Х (к) -векторлар тізбегінің Х векторына жинақталуы үшін
шартының орындалуы қажетті және жеткілікті. Бұл шарт кубтық норма үшін айқын, ал қалған екі норма үшін бұл шарттың орындалуы (1. 4), (1. 5) теңсіздіктерінен шығады. Сондықтан итерациялық әдістердің жинақталуын зерттегенде, векторлардың кез-келген, жоғарыда көрсетілген нормаларын пайдалануға болады.
1. 2. Матрицалардың нормалары.
Анықтама. Берілген А квадрат матрицаның нормасы-
деп теріс емес және келесі төрт шартты қанағаттандыратын санды айтамыз:
- , егержәне=0, егер А=0;
- ;
- ;
- .
Матрицаның нормасын әртүрлі жолдармен алуға болады. Мысалы көп қолданылатын нормаларға мына нормаларды жатқызуға болады:
,
.
Бұл нормалар бірінші үш шартты қанағаттандыратыны айқын болғандықтан 4-ші шарттың орындалуын дәлелдейік:
Айталық, А=(а іj ), B=(b іj ) болсын. Онда
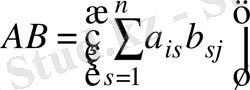
Сондықтан
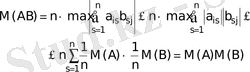
Дәл сол сияқты
.
Коши-Буняковский теңсіздігі бойынша
.
Осыдан
.
Яғни
.
3. Келісілген нормалар. Көптеген есептерде матрица мен вектордың нормалры қатар қолданылатындықтан, олар бір-бірімен келісілген болуы тиіс.
Анықтама . Егер А матрицасы мен Х векторы үшін
шарты орындалса, онда А матрицасы мен Х векторының нормалары келісілген дейміз.
Матрицаның М(А) нормасы вектордың кубтық, октаэдрлік, сфералық нормаларымен келісілген, ал N(A) тек сфералық нормамен келісілген.
Енді Х векторының нормасымен келісілген А матрицасының, шамасы жағынан ең кіші, нормасын табуды қарастырайық.
А матрицасының нормасы ретінде X =1 болған жағдайдағы АХ векторының ең үлкен нормасын алсақ, яғни
(1. 7)
болса, онда бұл шама норманың анықтамасының барлық төрт шартын қанағаттандырумен қатар келісілгендіктің де шартын қанағаттандырады:
1-шарт . Айталық,
. Онда X =1 вектор табылып,
болады. Сондықтан
болғандықтан
>0. Егер А =0 болса, онда
.
2-шарт . Екінші шарттың орындалуы мына теңдіктерден шығады:
.
Келісілгендік шарт.
Егер кез-келген вектор
болса, онда
векторының нормасы Х =1. Сондықтан
.
3-шарт. А+В матрицасы үшін A+B = (A+B) X 0 теңдігі орындалатындай нормасы бірге тең (( X 0 =1) Х 0 векторын табамыз. Сонда
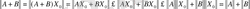
4-шарт. АВ матрицасы үшін X 0 =1 және ABХ 0 = AB теңдігін қанағаттандыратын Х 0 векторын табамыз. Сонда
.
Сонымен біз (1. 7) нормасы норманың анықтамасының барлық шарттарын және келісілгендік шартын көрдік. А матрицасының (1. 7) түріндегі нормасын берілген вектордың нормасына бағынған норма дейміз.
Енді бағынған норманың мәні басқа келісілген нормалардың мәнінен үлкен еместігін көрсетейік. Шынында да, матрицаның L(A) -вектордың нормасымен келісілген нормасы, ал
-вектордың нормасына бағынған нормасы болсын.
Онда нормасы бірге тең Х 0 векторы табылып A = AХ 0 теңдігі орындалады. Ал
екенін ескерсек, онда
екенін көреміз.
Енді жоғарыда көрсетілген вектордың нормаларына бағынған матрицаның нормасын қарастырайық:
- .
Бұл нормаға бағынған матрицаның нормасы
. (1. 8)
Шынында да, Х 1 =1 болсын. Сонда
, яғни
. Енді
шынында да
өрнегіне тең екенің дәлелдейік.
Ол үшін X 0 =1 және
болатын Х 0
векторын тұрғызайық. Айталық,
өзінің ең үлкен мәнін і=j болғанда қабылдасын. Ал Х 0 векторының координатасын

деп алсақ, онда X 0 = 1. Сонымен қоса
және
,
болғандықтан
.
Осыдан
.
Сонымен

.
2.
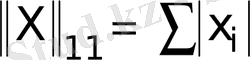
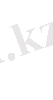
Бұл нормаға бағынған матрицаның нормасы-
. (1. 9)
Шынында да
болса, онда

Енді Х 0 векторын былайша алайық:
өрнегі өзінің ең үлкен мәнін k=j болғанда алатын, ал k≠j болғанда Х k (0) = 0және Х j (0) = 1 болсын. Сонда
.
Сонымен
.
3.
.
Бұл нормаға бағынған матрицаның нормасы-

мұнда л- А * А матрицасының ең үлкен меншікті саны. Шынында да,
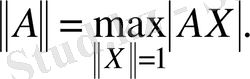
Бірақ AX 2 = АХ, АХ = Х, А * АХ , ал А * А -эрмиттік (симметриялы оң анықталған) матрица. Айталық, л 1 ең үлкен меншікті сан болсын, онда X =1 болғанда мах( Х, А * АХ ) = л 1 .
Сондықтан (1. 10) формуласы арқылы табылған матрицаның нормасын - спектрлік норма дейді. Осы формуланы пайдаланып А -1 кері матрицасының спектрлік нормасын анықтауға болады:
, мұнда л k (А'A) - A'A матрицасының меншікті сандары.
Матрицалар мен векторлар тізбегінің жинақталуы.
Сызықтық алгебрадағы шектер туралы түсініктер көбіне итерациялық әдістерді қарастырған кезде пайдаланылады. Сондықтан біз матрица мен векторлар тізбектерінің жинақталуы туралы ұғымды және матрица мен векторлар тізбегінің жинақталу шаттарын қарастырамыз.
Матрицалар мен векторлар тізбегінің шегі туралы түсінік.
Айталық, берілген
векторлар тізбегінің координаталары
х 1 (1) , …, х n (к) , …; … ; х 1 (k) , … х n (k) болсын.
Егер { X (к) } тізбегі Х= ( x 1 , x 2 , …, x n ) векторына жинақталатын болса, онда оны былайша жазады:
, немесе Х (к)
Х .
Бұл жағдай
(і=1, …, n) болғанда орындалады.
Ал
жинақталатын қатар дейміз, егер
бар болса және мұны қатардың қосындысы дейміз.
Енді А (1) , А (2) , …, А (к) , … матрицалар тізбегі берілсін және әрбір А (к) ={ a іj ( k ) } болсын. Егер барлық і, j үшін
шарты орындалса, онда { А ( k ) } тізбегі А ={ a іj } матрицасына жинақталады дейміз және оны былай жазады:
, немесе A ( к )
A .
Егер квадрат матрицалар тізбегі { А ( k ) } ерекше емес А матрицасына жинақталатын болса, онда жеткілікті үлкен к үшін А ( k ) матрицасының кері матрицасы бар болады және
.
Шынында да, егер A (к)
A болса, онда A (к) матрицасына сыбайлас матрица - В (к) , А матрицасына сыбайлас В матрицасына жинақталады. Себебі В (к) мен В -ның элементтері тиісінше А (к) мен А -ның элементтерінең тұратын полином.
Сол себебті
және к -ның белгілі бір мәнінен бастап
. Осыдан ( A (к) ) -1
A -1 , себебі
.
Теорема. Егер А матрицасы {А (k) } тізбегінің, ал F-{F (k) } тізбегінің шегі болса, онда А (k) Х (k) = F (k) жүйесінің шешімі
АХ=F жүйесінің шешіміне жинақталады.
Егер матрицаның элементтері t параметрі бойынша дифференциалданатын болса, онда
.
Егер A (t) ={ a іj ( t ) } 1 n болса, онда A '( t ) ={ a ' іj ( t ) } 1 n және мына дифференциялдау ережелері орындалады:
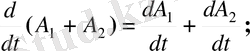
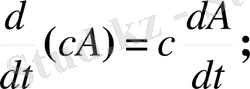
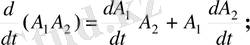
Жинақтылық теоремалары.
2. 1-Теорема. А m
0 болуы үшін, А матрицасының барлық меншікті санының модулі бірден кіші болуы қажетті және жеткілікті.
2. 2-Теорема.
болуы үшін А матрицасының ең болмағанда бір нормасы A<1 болуы жеткілікті.
2. 3-Теорема. Матрицаның кез-келген нормасының мәнінен меншікті санының модулінің мәні үлкен болмайды.
2. 4-Теорема.
қатары (Е-А) -1 матрицасына жинақталуы үшін
болуы қажетті және жеткілікті.
2. 5-Теорема. Егер A<1 болса, онда
.
2. 6-Теорема. Егер A< 1 болса, онда (Е-А) -1 бар болады және
.
Лекция 7. Гаусс әдісі .
Бізге
АХ=F (4. 1)
Теңдеулер жүйесі берілсін және
А
 0 дейік. Онда бұл жүйенің шешуін
0 дейік. Онда бұл жүйенің шешуін
Х=A -1 F түрінде жазуға болады. Осыдан (4. 1) теңдеулер жүйесін шешу үшін А -1 -ді табу керек. Бірақ А -1 -ді табу көптеген жағдайда тиімді болмағандықтан, оны таппай-ақ жүйенің шешуін іздестіретін жолдарды қарастыруға тура келеді. Сондай жолдардын кең тараған түрі Гаусс әдісі болып табылады. Онын әртүрлі есептеу алгоритмдері бар болғандықтан, біз тек бір ғана қарапайым түрін қарастырамыз.
Гаусс әдісінің есептеу алгоритмі.
Айталық,
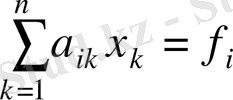 (
і
=1, …,
n
) (4. 2)
(
і
=1, …,
n
) (4. 2)
теңдеулер жүйесін шешу керек болсын.
Егер (4. 2) жүйесінің матрицасының элементтері і>k болғанда a іk =0 болса, онда (4. 2) жүйенің шешуі былайша табылады :
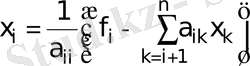 (
і
=1, …,
n
) . (4. 3)
(
і
=1, …,
n
) . (4. 3)
Сондықтан Гаусс әдісі берілген жүйенің матрицасын үшбұрышты матрица түріне түрлендіруге негізделген.
Бұл түрлендіру былайша жүргізіледі.
Айталық, (4. 2) жүйесінде
а
11
 0 болсын. (ал
а
11
=0 болса, онда жүйеден
а
kl
0 болсын. (ал
а
11
=0 болса, онда жүйеден
а
kl
 0 коэффициенті бар теңдеуді бірінші теңдеумен алмастырамыз) Бірінші теңдеуді
а
11
-ге бөлу арқылы
0 коэффициенті бар теңдеуді бірінші теңдеумен алмастырамыз) Бірінші теңдеуді
а
11
-ге бөлу арқылы
х 1 + С 12 х 2 + . . . + С 1 n x n =y 1 (4. 5)
теңдеуін аламыз. Мұнда
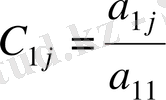 , (j=2, …,
n
) ,
, (j=2, …,
n
) ,
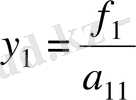 .
.
Енді қалған
a і 1 x 1 + a і 2 x 2 +…+ a іn x n =f і ( і =2, …, n ) (4. 6)
теңдеулер жүйесінен (4. 5) теңдеуін a і 1 -ге көбейтіп алып тастасақ, онда мынандай теңдеулер жүйесін аламыз.
x 1 + С 12 х 2 + . . . + C 1 j x j + . . . + C 1 n x n = y 1
a 22 (1) x 2 + . . . + a 2j (1) x j + . . . +a 2 n (1) x n = f 2 (1) (4. 7)
- - - - - - - - - -
a n 2 (1) x 2 + . . . + a nj (1) x j + . . . +a nn (1) x n =f n (1)
Мұнда a іj (!) = a іj - C 1 j a і 1,
f і (1) = f і -y 1 a і 1 ( і, j =2, 3, …, n ) (4. 8)
(4. 7) теңдеулер жүйесінде х 1 белгісізі тек бірінші теңдеуде болғандықтан, егер
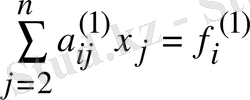 (
і
=2, …,
n
) (4. 9)
(
і
=2, …,
n
) (4. 9)
теңдеулер жүйесін қарастырамыз. Егер
а
22
(1)
 0 болса, онда жоғарыдағы тәсілді қолдану арқылы мына теңдеулер жүйесіне келеміз:
0 болса, онда жоғарыдағы тәсілді қолдану арқылы мына теңдеулер жүйесіне келеміз:
x 1 + C 12 x 2 + . . . + C 1 n x n =y 1
x 2 + C 23 x 3 +…+ C 2 n x n =y 2
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz