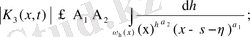Ерекшелігі әлсіз ядролы интегралдық теңдеулер: Фредгольм мен Вольтерра теңдеулерін регуляризациялау және симметриялық ядролардың қасиеттері


- Ерекшелігі әлсіз ядролы интегралдық теңдеулер
1. Фредгольм теңдеуі. Ақырлы
 облысында көп аргументті теңдеу қарастырайық.
облысында көп аргументті теңдеу қарастырайық.
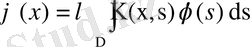 , (38)
, (38)
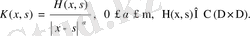 (39)
(39)
(38) түріндегі теңдеуді ерекшелігі әлсіз ядролы интегралдық теңдеу, ал (39) түріндегі ядроны ерекшелігі әлсіз немесе полярлық ядро деп атайды. Егер
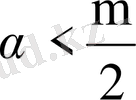 болса, онда
болса, онда
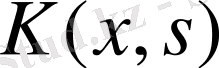 Фредгольм ядросы деп аталады. Расында,
Фредгольм ядросы деп аталады. Расында,
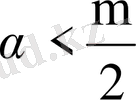 болған жағдайда:
болған жағдайда:
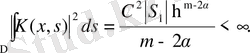
Мұндағы
 кеңістігіндегі радиусы бірге тең сфера бетінің ауданы, ал h - D облысының диаметрі.
кеңістігіндегі радиусы бірге тең сфера бетінің ауданы, ал h - D облысының диаметрі.
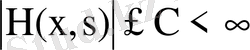 болғандықтан,
болғандықтан,
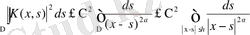
орынды. Бұл соңғы интегралда центрі х нүктесінде болатын сфералық координаталарға көшсек және
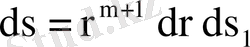 екенін ескерсек
екенін ескерсек

 болсын. Ол кезде
болсын. Ол кезде
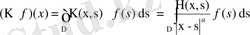
D облысында үзіліссіз функция болады.
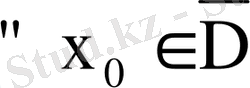 нүктесін бекітіп және
нүктесін бекітіп және
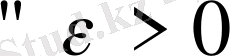 деп алайық. Сонда
деп алайық. Сонда
 .
.
Бұл өрнектің оң жағындағы 1- интеграл (40) теңсіздігіне байланысты
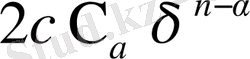 шамасынан үлкен бола алмайды, ендеше
шамасынан үлкен бола алмайды, ендеше
 - ны жеткілікті дәрежеде кішірейтіп бірінші интегралды
- ны жеткілікті дәрежеде кішірейтіп бірінші интегралды
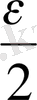 - ден кіші етуге болады. Ал екінші интеграл астындағы өрнектер
- ден кіші етуге болады. Ал екінші интеграл астындағы өрнектер
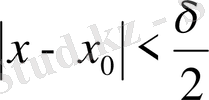 мен
мен
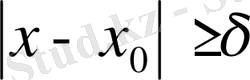 облыстарында
облыстарында
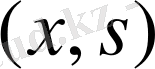 аргументтері бойынша бірқалыпты үзіліссіз, сондықтан барлық,
аргументтері бойынша бірқалыпты үзіліссіз, сондықтан барлық,
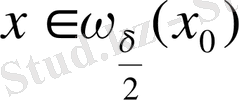 үшін ол интегралды әрқашан
үшін ол интегралды әрқашан
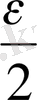 - ден кіші етуге болады. Демек, барлық
- ден кіші етуге болады. Демек, барлық
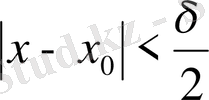 үшін
үшін
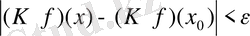 . Бұл
. Бұл
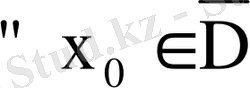 нүктесінде
нүктесінде
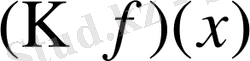 - тің үзіліссіз екенін көрсетеді, яғни
- тің үзіліссіз екенін көрсетеді, яғни
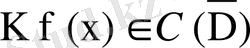 . Олай болса,
. Олай болса,

теңсіздігі орынды.
Енді
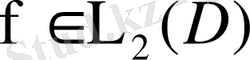 болсын. Коши- Буняковский теңсіздігін пайдалансақ,
болсын. Коши- Буняковский теңсіздігін пайдалансақ,

Бұл K операторының
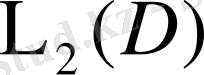 кеңістігін
кеңістігін
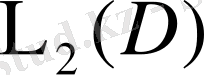 - ға бейнелейтінін көрсетеді.
- ға бейнелейтінін көрсетеді.
Осы дәлелденген лемманы және өткен параграфтағы тұжырымдарды пайдалансақ, ерекшелігі әлсіз ядролы (38) интегралдық теңдеуінің шектелген
 облысында
облысында
 және
және
 болғанда Нейман қатары түріндегі жалғыз шешімі бар болады, ол қатар
болғанда Нейман қатары түріндегі жалғыз шешімі бар болады, ол қатар
 облысында бірқалыпты жинақты. Сонымен бірге жоғарыдағы ерекшелігі әлсіз (39) ядролы (38) интегралдық теңдеуін ядросы шектелген эквивалентті интегралдық теңдеумен ауыстырып шешуге болады.
облысында бірқалыпты жинақты. Сонымен бірге жоғарыдағы ерекшелігі әлсіз (39) ядролы (38) интегралдық теңдеуін ядросы шектелген эквивалентті интегралдық теңдеумен ауыстырып шешуге болады.
Алдымен мына лемманы дәлелдейік.
1-лемма. Егер
 болып және
болып және
 шектелген облыс болса, онда
шектелген облыс болса, онда
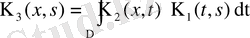 (41)
(41)
полярлық ядро, оның үстіне
(42)
болады.
Дәлелдеуі. Егер
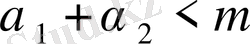 болса,
болса,
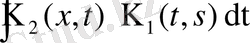 интегралының
интегралының
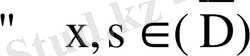 үшін бірқалыпты жинақты екені түсінікті, сондықтан
үшін бірқалыпты жинақты екені түсінікті, сондықтан
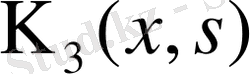 ядросы
ядросы
 облысында үзіліссіз. Лемманы толық дәлелдеу үшін
облысында үзіліссіз. Лемманы толық дәлелдеу үшін
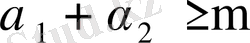 болғанда (42) теңсіздігін дәлелдейік. (41) ядросын бағалау нәтижесінде
болғанда (42) теңсіздігін дәлелдейік. (41) ядросын бағалау нәтижесінде
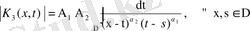
екенін аламыз. Бұл теңсіздікке
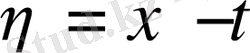 ауыстыруын негізіп, D облысын диаметрі h болған
ауыстыруын негізіп, D облысын диаметрі h болған
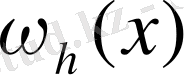 шарына ауыстырсақ,
шарына ауыстырсақ,
енді
 белгілеулерін енгізіп және интегралдағы айнымалыларды
белгілеулерін енгізіп және интегралдағы айнымалыларды
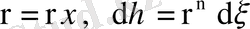 етіп ауыстырсақ,
етіп ауыстырсақ,

Бұл теңсіздіктің оң жағындағы бірінші интеграл
 болғандықтан шектелген шама, яғни
болғандықтан шектелген шама, яғни
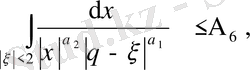
ал
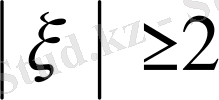 болған кезде
болған кезде
 екенін ескеріп, екінші интегралды бағаласақ,
екенін ескеріп, екінші интегралды бағаласақ,

міне осы соңғы теңсіздіктерден (42) өрнегінің орынды екені шығады.
Салдар. Егер ядро әлсіз ерекшелікті болса, оның қайталанған ядролары қайсыбір номерінен бастап шектелген болады.
Расында,
 ядросының n қайталанушы ядросы, 2- лемма бойынша
ядросының n қайталанушы ядросы, 2- лемма бойынша
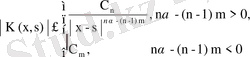
түрінде бағаланады, бұндағы C
n
шектелген тұрақты шама. Әрине, бұл өрнек шектелген (егер
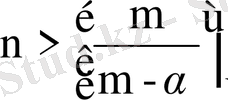 ) болса. Барлық уақытта жоғарыдағы (39) түріндегі ерекшелігі әлсіз ядролы (38) интегралдық теңдеуін ядросы қайталанған
) болса. Барлық уақытта жоғарыдағы (39) түріндегі ерекшелігі әлсіз ядролы (38) интегралдық теңдеуін ядросы қайталанған
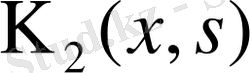 немесе
немесе
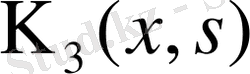 ,
,
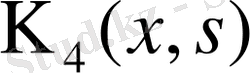 , . . . ядролармен ауысқан сол типтегі теңдеулерге келтіруге болады. Ол үшін (38) теңдеуіндегі х- ті s- пен, ал s- ті t- мен ауыстырып, онда кейін теңдеуді
, . . . ядролармен ауысқан сол типтегі теңдеулерге келтіруге болады. Ол үшін (38) теңдеуіндегі х- ті s- пен, ал s- ті t- мен ауыстырып, онда кейін теңдеуді
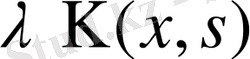 - ке көбейтіп, пайда болған өрнекті s бойынша интегралдап,
- ке көбейтіп, пайда болған өрнекті s бойынша интегралдап,

теңдеуін аламыз. Бұл теңдіктен және (38) теңдігінен
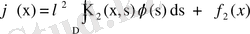
екені шығады, мұндағы
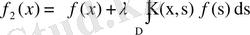 .
.
Дәл осылай
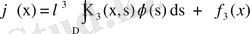 ,
,
ал мұнда
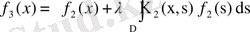 міне осылай жалғаса береді.
міне осылай жалғаса береді.
Бұл процесті шектелген санақты түрде қайталап ядросы
 шектелген, үзіліссіз болған Фредгольмнің 2- текті интегралдық теңдеуін аламыз. Демек ерекшелігі әлсіз ядролы интегралдық теңдеуді регулялы ядролы интегралдық теңдеуге келтірдік.
шектелген, үзіліссіз болған Фредгольмнің 2- текті интегралдық теңдеуін аламыз. Демек ерекшелігі әлсіз ядролы интегралдық теңдеуді регулялы ядролы интегралдық теңдеуге келтірдік.
2. Вольтерра теңдеуі. Ерекшелігі әлсіз ядролы

теңдеуге келтіруге болады. Мұнда
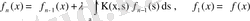 .
.
- лемма. Егер (43) теңдеуінің ядросы
түрінде болса, онда ол теңдеудің ядросы қайталанушы
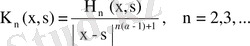
түрінде болады, бұнда
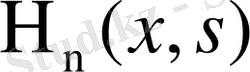 кез келген шектелген функция.
кез келген шектелген функция.
Дәлелдеуі. Алдымен
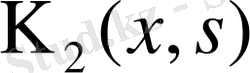 жағдайын қарастырайық:
жағдайын қарастырайық:
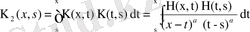 ,
,
бұған
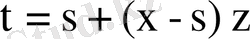 деп жаңа айнымалы енгізсек,
деп жаңа айнымалы енгізсек,
 ,
,
бұнда
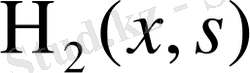 шектелген үзіліссіз функция, себебі бұл соңғы өрнектегі интеграл
шектелген үзіліссіз функция, себебі бұл соңғы өрнектегі интеграл
 болғанда жинақты. Осы процесті қайталап,
болғанда жинақты. Осы процесті қайталап,
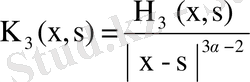 , . . . ,
, . . . ,
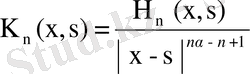 , . . . (43)
, . . . (43)
қатыстарын аламыз. Ал осы өрнектерден белгілі бір n номерінен бастап
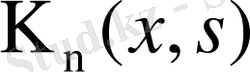 ядросы шектелген, демек осындай ерекшелігі әлсіз (43) интегралдық теңдеуі Вольтерраның шектелген ядролы теңдеуіне келеді. Сонымен ерекше ядролы Вольтерраның интегралдық теңдеуін ядросы шенелген интегралдық теңдеуге ауыстырдық. Соңғы теңдеуді біртіндеп жуықтау әдісімен шешеді, ол шешім
ядросы шектелген, демек осындай ерекшелігі әлсіз (43) интегралдық теңдеуі Вольтерраның шектелген ядролы теңдеуіне келеді. Сонымен ерекше ядролы Вольтерраның интегралдық теңдеуін ядросы шенелген интегралдық теңдеуге ауыстырдық. Соңғы теңдеуді біртіндеп жуықтау әдісімен шешеді, ол шешім
 - ның кез келген мәні үшін табыдады.
- ның кез келген мәні үшін табыдады.
- Симметриялық ядролар және олардың кейбір қасиеттері
кеңістігінде
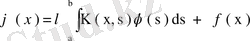
интегралдық теңдеуін қарастырайық. Егер нақты ядро
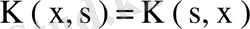 шартын қанағаттандырса, оны симметриялық ядро деп атайды. Мысалы,
шартын қанағаттандырса, оны симметриялық ядро деп атайды. Мысалы,

симметриялық ядролар. Комплекстік
 ядросы
ядросы
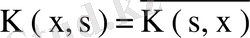 шартын қанағаттандырса, оны симметриялық эрмиттік ядро деп атайды. Ядросы симметриялық ядро болатын интегралдық теңдеуді симметриялық интегралдық теңдеу деп айтады.
шартын қанағаттандырса, оны симметриялық эрмиттік ядро деп атайды. Ядросы симметриялық ядро болатын интегралдық теңдеуді симметриялық интегралдық теңдеу деп айтады.
Егер
 симметриялық (эрмиттік) ядро болса, онда бұл ядроның қайталанған ядролары симметриялық болады. Расында, қайталанған ядро анықтамасы бойынша
симметриялық (эрмиттік) ядро болса, онда бұл ядроның қайталанған ядролары симметриялық болады. Расында, қайталанған ядро анықтамасы бойынша

Дәл осылай жалпы жағдай үшін де бұл қасиеттің орынды екенін оңай көруге болады.
Егер
 симметриялық эрмиттік ядро болса, онда Фредгольм орераторы
симметриялық эрмиттік ядро болса, онда Фредгольм орераторы
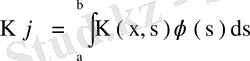
өзіне түйіндес, яғни
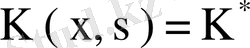 болады. Расында
болады. Расында
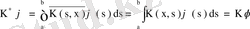 .
.
Біз бұдан былай нақты аргументті симметриялық ядроларды қарастырамыз.
- Фредгольмнің жалпы интегралдық теңдеуін ерекшеленген ядролы теңдеуге келтіру.
Фредгольмнің ерекшеленген ядролы интегралдық теңдеуін шешу мәселесін екі интегралдық теңдеуді шешуге келтіреміз: ол теңдеулердің біреуі біртіндеп жуықтау әдісімен, яғни резольвента арқылы шешіледі, ал екіншісі ерекшеленген ядролы теңдеу. Бұл жағдайда
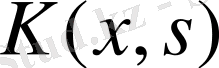 ядросы өзіне жуық ерекшеленген ядромен аппроксимацияланады. Мұндай аппроксимациялауды бірнеше жолмен орындауға болады. Мәселен, егер
ядросы өзіне жуық ерекшеленген ядромен аппроксимацияланады. Мұндай аппроксимациялауды бірнеше жолмен орындауға болады. Мәселен, егер
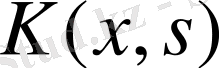 ядросы
ядросы
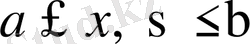 облысында бірқалыпты жинақты дәрежелік немесе қос тригонометрикалық қатарға жіктелсе, онда
облысында бірқалыпты жинақты дәрежелік немесе қос тригонометрикалық қатарға жіктелсе, онда
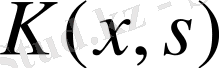 ядросына дәрежелік немесе тригонометриялық қатардың
ядросына дәрежелік немесе тригонометриялық қатардың
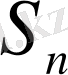 дербес қосындысы мен жуықтауға болады, ал
дербес қосындысы мен жуықтауға болады, ал
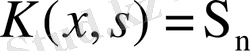 айырымы жинақталатын қатардың қалдығы болғандықтан ақырсыз аз шама.
айырымы жинақталатын қатардың қалдығы болғандықтан ақырсыз аз шама.
Фредгольмнің 2- текті
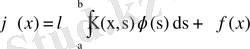 (49)
(49)
теңдеуін қарастырайық. Бұл теңдеудегі ядро
 , яғни
, яғни
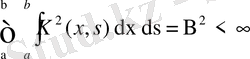
болсын.
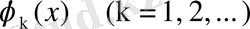 функциялары
функциялары
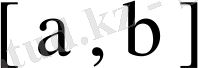 аралығында ортонормаланған және ол система толық болсын. Белгілі
аралығында ортонормаланған және ол система толық болсын. Белгілі
 ядросын
ядросын
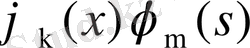 функцияларымен Фурье қатарына
функцияларымен Фурье қатарына
 (50)
(50)
жіктеуге болады. Бұл қатар
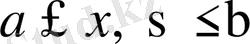 болғанда орташа мағынада жинақты.
болғанда орташа мағынада жинақты.
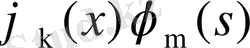 функциялары системасы
функциялары системасы
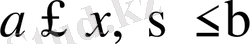 облысында толық болғандықтан, Парсевальдың тұйықтық шарты
облысында толық болғандықтан, Парсевальдың тұйықтық шарты
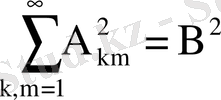 (51) орынды. Егер (50) қатарының дербес қосындысын
(51) орынды. Егер (50) қатарының дербес қосындысын

деп белгілесек, ол ерекшеленген ядро болады.
Енді
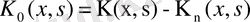 деп белгілейік. Сонда
деп белгілейік. Сонда
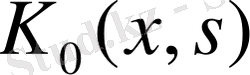 функциясы (50) - Фурье қатарының қалдығы болады:
функциясы (50) - Фурье қатарының қалдығы болады:
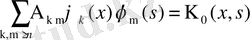
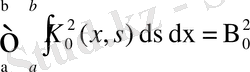
деп белгілейік. . осы қатарға тұйықтық шартын пайдалансақ:
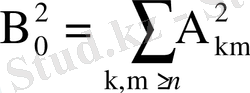
өрнегін аламыз. Алынған қатар жинақталатын (51) қатарының қалдығы, сондықтан соңғы қатар қосындысы n жеткілікті дәрежедегі аз шама. Сондықтан n- ның үлкен мәндерінде
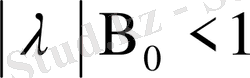 теңсіздігі орындалады, бұл шартты қанағаттандыратын
теңсіздігі орындалады, бұл шартты қанағаттандыратын
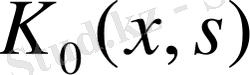 - ті кішкентай ядро деп айтамыз.
- ті кішкентай ядро деп айтамыз.
Сонымен
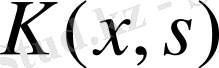 ядросы
ядросы
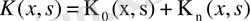 түріндегі (
түріндегі (
 - ерекшеленген, ал
- ерекшеленген, ал
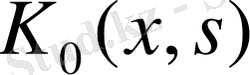 кішкентай ) ядроларға жіктеледі. Енді (49) теңдеуі ядросын соңғы теңдіктегі қосындымен ауыстырып
кішкентай ) ядроларға жіктеледі. Енді (49) теңдеуі ядросын соңғы теңдіктегі қосындымен ауыстырып
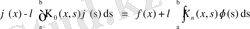
өрнегін аламыз. Осы теңдіктің оң жағындағы өрнекті
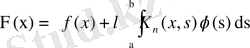
деп белгілесек, онда

теңдеуін аламыз. Бұрынғы дәлелдеулер бойынша
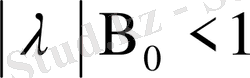 шарты орындалғанда бұл теңдеудің жалғыз шешімі бар болады, ол шешім
шарты орындалғанда бұл теңдеудің жалғыз шешімі бар болады, ол шешім
 ядросының резольвентасы
ядросының резольвентасы
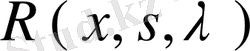 арқылы өрнектеледі:
арқылы өрнектеледі:
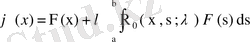 .
.
Ал F (x) функциясын оның мәнімен ауыстырсақ,
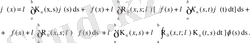
Енді
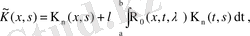
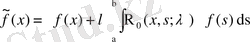
деп белгілесек, теңдеуді
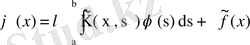
түріне келтіреміз. Әрине, бұндағы
 - ерекшеленген ядро, себебі,
- ерекшеленген ядро, себебі,
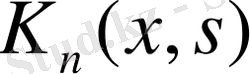 ядросы тозғындалған:
ядросы тозғындалған:
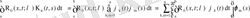 .
.
Сонымен, (49) түріндегі кез келген интегралдық теңдеуді ерекшеленген ядролы теңдеуге келтіруге болады. Міне осы жағдайды пайдаланып ерекшеленген ядролы интегралды теңдеу үшін Фредгольм теоремасы үзіліссіз ядролы немесе ядросы
 - де болатын кез келген Фредгольмнің 2- текті интегралдық теңдеуі үшін орынды деп айта аламыз.
- де болатын кез келген Фредгольмнің 2- текті интегралдық теңдеуі үшін орынды деп айта аламыз.
Ескерту. Қолданбалы есептерде бұл теорияны пайдаланғанда
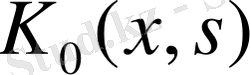 ядросын қажетті дәрежеде аз етіп алып, оны ескермей, бірден белгісіз функциясы
ядросын қажетті дәрежеде аз етіп алып, оны ескермей, бірден белгісіз функциясы
 , оң жағы
, оң жағы
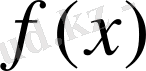 болған ерекшеленген ядролы интегралдық теңдеуді шешеді. Бұл жағдайда ядросы
болған ерекшеленген ядролы интегралдық теңдеуді шешеді. Бұл жағдайда ядросы
 ерекшеленген интегралдық теңдеудің шешімі ерекшеленбеген теңдеудің шешімінен өте аз шамада ғана айырмашылықта болатынын көрсету оңай
ерекшеленген интегралдық теңдеудің шешімі ерекшеленбеген теңдеудің шешімінен өте аз шамада ғана айырмашылықта болатынын көрсету оңай
29. Ядроны қатарға жіктеу
Симметриялық
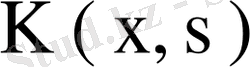 ядросын қарастырайық. Оның меншікті мәндері
ядросын қарастырайық. Оның меншікті мәндері
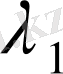 ,
,
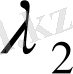 , . . . ,
, . . . ,
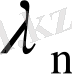 , . . . , ал меншікті функциялары
, . . . , ал меншікті функциялары
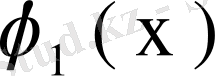 ,
,
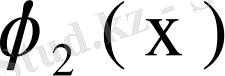 , . . . ,
, . . . ,
 , . . . болсын. Меншікті функциялар ортонормаланған, ал меншікті мәндер абсолют шамаларының өсу ретімен орналасқан болсын. Жаңадан
, . . . болсын. Меншікті функциялар ортонормаланған, ал меншікті мәндер абсолют шамаларының өсу ретімен орналасқан болсын. Жаңадан
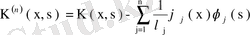 (76)
(76)
симметриялық ядросын құрайық.
4- лемма.
 ,
,
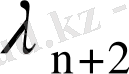 , . . . ,
, . . . ,
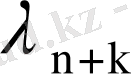 , . . . ;
, . . . ;
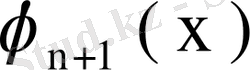 ,
,
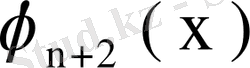 , . . . ,
, . . . ,
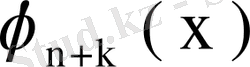 , . . . тізбектері симметриялық
, . . . тізбектері симметриялық
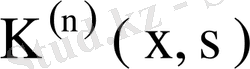 ядросының меншікті мәндері мен оларға сәйкес меншікті функциялары болады.
ядросының меншікті мәндері мен оларға сәйкес меншікті функциялары болады.
Дәлелдеуі.
 болсын. Бірінші тізбектен
болсын. Бірінші тізбектен
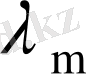 - ді, ал екінші тізбектен оған сәйкес келуші
- ді, ал екінші тізбектен оған сәйкес келуші
 функциясын алып,
функциясын алып,

өрнегін құрайық. Енді
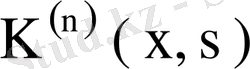 ядросын (76) өрнегімен ауыстырып мынадай теңдік аламыз:
ядросын (76) өрнегімен ауыстырып мынадай теңдік аламыз:
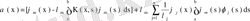 .
.
Бұндағы
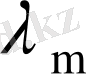 мен
мен

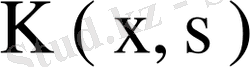 ядросының меншікті мәні мен меншікті функциясы болғандықтан, квадрат жақшадағы өрнек нольге тең және
ядросының меншікті мәні мен меншікті функциясы болғандықтан, квадрат жақшадағы өрнек нольге тең және
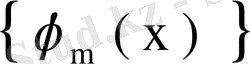 функциялары системасы ортонормаланғандықтан,
функциялары системасы ортонормаланғандықтан,
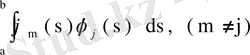
Демек,
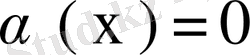 , яғни
, яғни
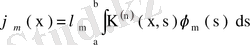 , олай болса,
, олай болса,
 жағдайында
жағдайында
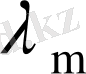 мен
мен
 -
-
 ядросының меншікті мәні мен меншікті функциясы.
ядросының меншікті мәні мен меншікті функциясы.
Керісінше, егер
 ядросы үшін
ядросы үшін
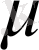 саны мен
саны мен
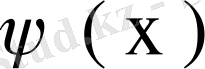 функциясы меншікті мән мен меншікті функция болса, онда олар
функциясы меншікті мән мен меншікті функция болса, онда олар
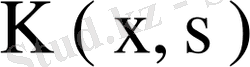 ядросының меншікті мәндері мен меншікті функцияларының жиындарынан табылады. Ұйғарым бойынша
ядросының меншікті мәндері мен меншікті функцияларының жиындарынан табылады. Ұйғарым бойынша
 мен
мен
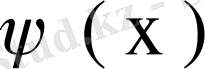

теңдеуін қанағаттандырады. Бұл теңдіктегі
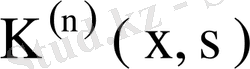 ядросын (76) өрнегі бойынша ауыстырсақ,
ядросын (76) өрнегі бойынша ауыстырсақ,
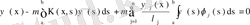 (77)
(77)
Бұл теңдеудің екі жағын да
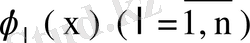 функциясына скаляр көбейтіп,
функциясына скаляр көбейтіп,
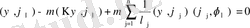
теңдеуіне келеміз.
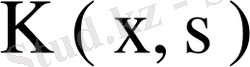 ядросының симметриялық және
ядросының симметриялық және
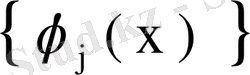 функцияларының ортонормаланған қасиетін ескерсек,
функцияларының ортонормаланған қасиетін ескерсек,

өрнектерін аламыз. Бұл жағдайда алдыңғы теңдеуден
 ортогоналдық шарты шығады. . онда (77) теңдеуі:
ортогоналдық шарты шығады. . онда (77) теңдеуі:

түрінде жазылады. Бұл теңдеуден
 мен
мен
 -
-
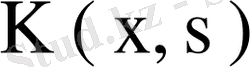 ядросының меншікті мәні мен меншікті функциясы екенін, ал
ядросының меншікті мәні мен меншікті функциясы екенін, ал
 - тің
- тің
 функцияларымен ортогональ болғандықтан
функцияларымен ортогональ болғандықтан
 ретті меншікті функциялардың біреуімен сай келетінін көреміз.
ретті меншікті функциялардың біреуімен сай келетінін көреміз.
Салдар. Егер
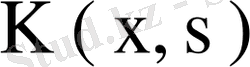 ядросының n- нен көп меншікті мәні бар болса, онда
ядросының n- нен көп меншікті мәні бар болса, онда
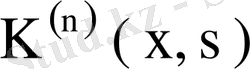 ядросының меншікті мәндерінің модулі бойынша ең кішісі
ядросының меншікті мәндерінің модулі бойынша ең кішісі
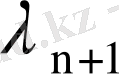 болады. Берілген ядроның меншікті мәндері
болады. Берілген ядроның меншікті мәндері
 ,
,
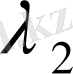 , . . . ,
, . . . ,
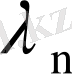 ақырлы санды болған жеке жағдайды қарастырайық. Онда
ақырлы санды болған жеке жағдайды қарастырайық. Онда
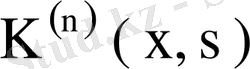 ядросының бірде- бір меншікті мәні болмайды. Бұндай жағдайда бұрын дәлелденген теорема бойынша
ядросының бірде- бір меншікті мәні болмайды. Бұндай жағдайда бұрын дәлелденген теорема бойынша
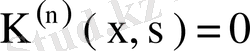 немесе
немесе
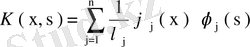 .
.
Осы формуладан
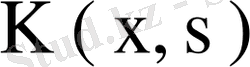 ядросының ерекшеленген ядро екенін көреміз. Кез келген ерекшеленген ядроның ақырлы санды меншікті мәндері бар болғандықтан және жоғарыдағы талдаулардан мына теорема орынды.
ядросының ерекшеленген ядро екенін көреміз. Кез келген ерекшеленген ядроның ақырлы санды меншікті мәндері бар болғандықтан және жоғарыдағы талдаулардан мына теорема орынды.
Дини теоремасы. Квадратымен интегралданатын симметриялық ядроның меншікті мәндері мен меншікті функциялары ақырлы санды болуы үшін оның ерекшеленген ядро болуы қажетті де жеткілікті.
Салдар. Кез келген квадратымен интегралданатын
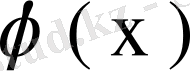 функциясы үшін
функциясы үшін
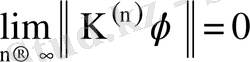 теңдігі орынды.
теңдігі орынды.
Дәлелдеуі. Егер
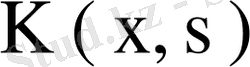 ерекшеленбеген ядро болса, соңғы теңдіктің орындалуы ап-айқын. Бірінші салдар бойынша
ерекшеленбеген ядро болса, соңғы теңдіктің орындалуы ап-айқын. Бірінші салдар бойынша
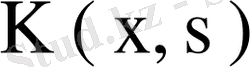 ядросы ерекшеленбеген болса, онда
ядросы ерекшеленбеген болса, онда
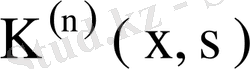 ядросының модулі бойынша ең кіші меншікті мәні
ядросының модулі бойынша ең кіші меншікті мәні
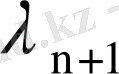 болады.
болады.
Жоғарыдағы (73) теңсіздігі бойынша
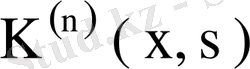 ядросы, оның меншікті мәні мен меншікті функциясы үшін
ядросы, оның меншікті мәні мен меншікті функциясы үшін
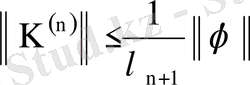
теңсіздік орынды және
 жағдайда
жағдайда
 болғандықтан соңғы өрнектен
болғандықтан соңғы өрнектен
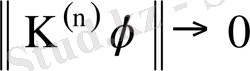 .
.
Тұрақты болған х үшін
 олай болса, ол ядро ортонормаланған
олай болса, ол ядро ортонормаланған
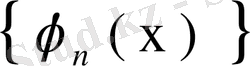 системасы бойынша
системасы бойынша

Фурье қатарына жіктеледі де, ал Фурье коэффициенттері
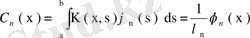
теңдігімен анықталады. Сонымен,
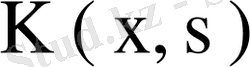 ядросына оның меншікті функциялар системасы
ядросына оның меншікті функциялар системасы
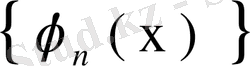 бойынша
бойынша
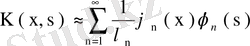
түріндегі бисызықты деп аталатын Фурье қатары сәйкес келеді екен. Бессель теңсіздігі бойынша
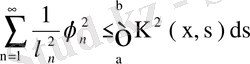 . (78)
. (78)
Бұл теңсіздіктегі қатар мүшелері оң және оларды мүшелеп х бойынша a- дан b- ға дейін интегралдап
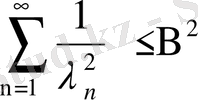 теңсіздігін аламыз, яғни
теңсіздігін аламыз, яғни
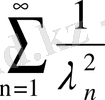 қатары жинақты. Енді
қатары жинақты. Енді
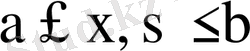 квадратында
квадратында
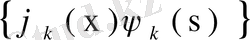 системасының ортонормаланғандығын және Рисс- Фишер теоремасын ескерсек, мынадай қорытындыға келеміз.
системасының ортонормаланғандығын және Рисс- Фишер теоремасын ескерсек, мынадай қорытындыға келеміз.
Теорема. Бисызықты қатар
 облысында орташа мағынада жинақты және ол қатардың қосындысы сол ядроға тең.
облысында орташа мағынада жинақты және ол қатардың қосындысы сол ядроға тең.
Енді қайталанған ядроларды жіктейік. Егер
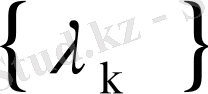 сандары мен
сандары мен
 функциялары
функциялары
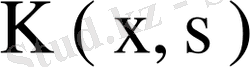 симметриялық ядросының меншікті мәндері мен меншікті функциялары болса, онда
симметриялық ядросының меншікті мәндері мен меншікті функциялары болса, онда
 қайталанатын ядросының меншікті мәндері
қайталанатын ядросының меншікті мәндері
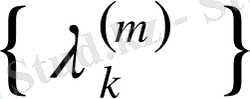 , ал меншікті функциялары
, ал меншікті функциялары
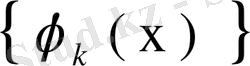 екені белгілі, яғни
екені белгілі, яғни
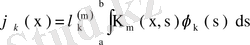 (79)
(79)
теңдігі орындалады.
 ядросын х аргументін тұрақтылап, ортонормаланған
ядросын х аргументін тұрақтылап, ортонормаланған
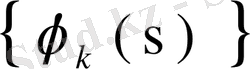 системасы бойынша Фурье қатарына жіктесек,
системасы бойынша Фурье қатарына жіктесек,
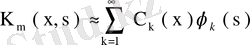 ,
,
мұндағы Фурье коэффициенттері
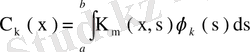
өрнегімен анықталады. Бұдан және (79) теңдігінен
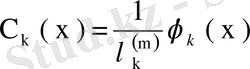 .
.
Сонымен
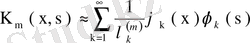 . (80)
. (80)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz