Евклид кеңістігінде дифференциалдық формалар мен сыртқы дифференциал

ІІ Дифференциалдық формалар

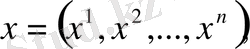
§1 . символымен п- өлшемді Евклид кеңістігіне тиісті болған ашық жиын болсын. облысының нүктелерін 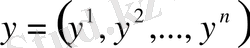символдарымен белгілейміз.

1-анықтама . облысында анықталған р- дәрежелі дифференциалдық форма деп әрбір фиксірленген -те 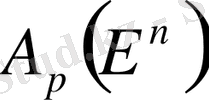кеңістігіне тиісті болған 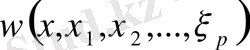функцияға айтамыз.

Демек, 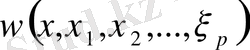дифференциалдық форма үшін 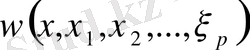ауыспа таңбалы р- форма.

облысында анықталған дифференциалдық р- формалар жиынын 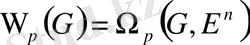символымен белгілейміз.

Біз мұнда фиксирленген үшін - р форма облысында шексіз дифференциалданатын функция деп есептейміз.

І-тараудың нәтижелері бойынша кез-келген - р форманы

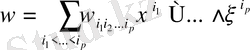(1)

теңдігімен анықтауға болады.

Төменде жазатын формулаларда 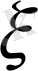векторын 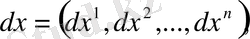ал 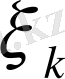векторларын 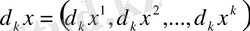символдарымен белгілейміз.

кеңістігінің базисі мысал ретінде 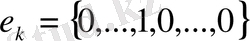(мұнда 1 - к -ші орында) векторларын аламыз.

базиске түйіндес базис 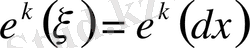болады. Бұл жерде

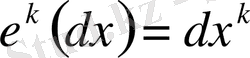
Осы белгілеулерден кейін (1) формула

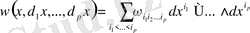
көрініске келеді.

1-мысал . Дифференциалдық 0-форма - облысында анықталған кез-келген шексіз дифференциалданушы функция.

2-мысал . Дифференциалдық 1-форма

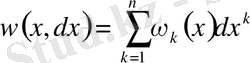
теңдікпен анықталады.

Егер n =1 болса 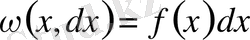болады.

1-дәрежелі дифференциалдық форманы кейде сызықтық дифференциалдық форма деп те атайды.

3-мысал . Дифференциалдық 2-форма түрі

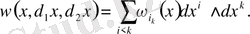
Анықтама бойынша

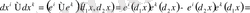
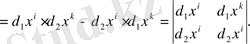
n= 2 болған дербес жағдайда

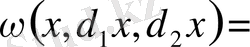
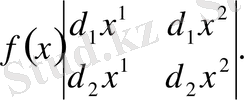
Егер n= 3 болса белгілерін енгізсек, онда

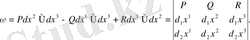
4-мысал . 3 өлшемді кеңістікте дифференциалдық 3-форма

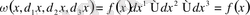
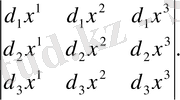
теңдігімен анықталады. Бұл теңдіктегі анықтауыш 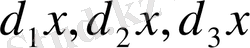векторларына сәйкес келетін элементтің көлеміне тең.

§2. Сыртқы дифференциал .

Анықтама . 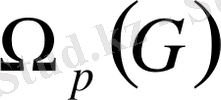жиынына тиісті болған 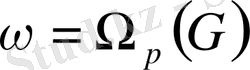р- сызықтық дифференциалдық форманың сыртқы дифференциалы деп 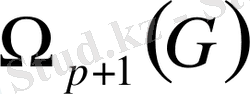жиынына тиісті

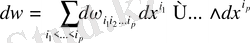
өрнегімен анықталатын 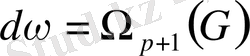формаға айтамыз.

Мұндағы

.

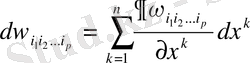Демек, егер де

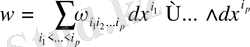
болса, онда

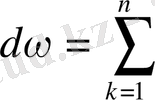
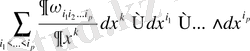
1-мысал. 0-дәрежелі дифференциалдық форма (яғни 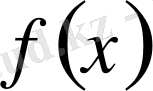функциясы)

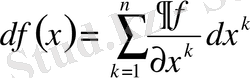
теңдігімен анықталады.

2-мысал . (*) сызықтық форманың дифференциалын есептейік

.

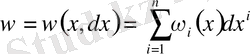Анықтама бойынша

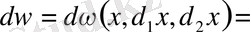
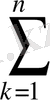
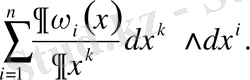
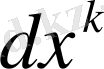және 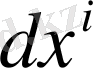векторлар үшін

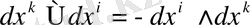және .

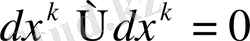Олай болса

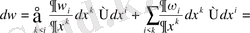
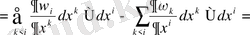
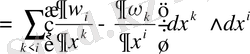
Егер n= 2 болса, онда 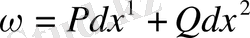үшін

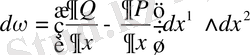
теңдігі келіп шығады.

§3. Сыртқы дифференциалдың қасиеттері .

Сыртқы дифференциалдың анықтамасынан мына қасиеттері келіп шығады:

1. егерболса, онда

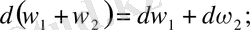
2. егержәне-нақты сан болса. Онда

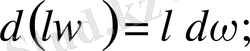
3. егерболса, онда

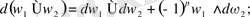
3) қасиетті дәлелдейік. Айталық

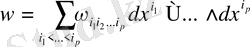
болсын.

Осы формаға сәйкес

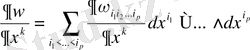
белгісін енгізейік.

Онда -ні

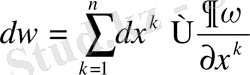
көріністе жазып алуға болады.

Егер 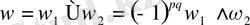болатынын және

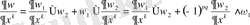
теңдігін есепке алсақ, онда

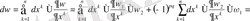
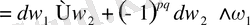
болады.

Бұған қосымша 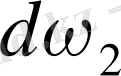форманың 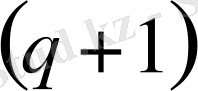- форма екенін есепке алсақ, онда

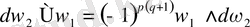
Нәтижеде

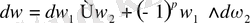
Мына теоремада сыртқы көбейтіндінің негізгі қасиетін баяндаймыз.

Теорема .

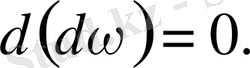
Дәлелдеуі. Алдымен -ні 0-форма деп есептейік, яғни 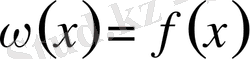болсын. Онда

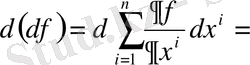
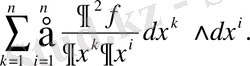
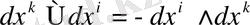теңдігін есепке алсақ, -ті

өрнектеуге болады. Бұдан 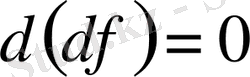болады.

Егер

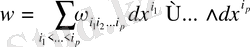
болса, онда

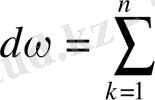
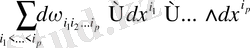
Бұл қосындының әрбір мүшесі 0-дәрежелі дифференциалдық форма болады, атап айтқанда олар

.

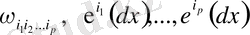Енді осы қосындыға сыртқы көбейтіндінің 3) -қасиетін қолданатын болсақ, онда 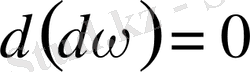болады.

Теорема дәлелденді.

---

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс