Гиперболалық параболоид

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 16 бет
Таңдаулыға:

Х ₁ lq + у ₁ тр-рqn = 0.

х - x ₁ l у - Уі т

Енді = =

z - z ₁ п z - z ₁ п

қатынастарын пайдаланып, іздеген теңдеуді табамыз:

х - x ₁ у - у ₁

q+у ₁ q ― рq = 0,

z - z ₁ z - z ₁

qхх ₁ - qх ₁ ² + руу ₁ - ру ₁ ² - рqz +рqz ₁ =0,

хх ₁ уу ₁ х ₁ ² у ₁ ²

+ = z - z ₁ + + ,

р q р q

хх ₁ уу ₁ х ₁ ² у ₁ ²

+ = z + z ₁ + + 2 z.

р q р q

Осыдан

хх ₁ уу ₁

+ = z + z ₁

р q

х ² у ²

Берілген + = z эллипстік параболоидтың дөңгелегіндегі

4 2

нүктелерді табайық.

Ш е ш у і. Бұл эллипстік параболоидтың дөңгелегіндегі нүктелерді табу үшін у + z = k жазықтыктарын жүргіземіз. Жанама жазықтыктар осы жазықтықгарға параллель болу керек. Жанама жазықтықтың теңдеуі

х ² у ²

+ = z + z ₁ ,

4 2

немесе

хх ₁ + 2уу ₁ - 2 z - 2 z ₁ = 0.

Бұл жазықтық мына у + z = k жазықтықтарына параллель. Сондықтан хх ₁ = 0, 2уу ₁ - 2 z - 2 z ₁ = 0. Осыдан х ₁ =0, уу ₁ - z - z ₁ = 0.

Мына у + z = k теңдеулеріндегі k коэффициентін табу үшін р және q параметрлері мен бұл коэффициенттің байланысын жазамыз: k р = q,

k ∙2=1, k = 1 . Осы k -ның мәнін бёрілген жазықтықтардың теңдеуіне

қойып, екі жазыктықтың теңдеуін жазайық:

у + z = 1 . Жанама жазықтық пен бұл жазықтықтар параллель.

Екі жазықтықтың параллельдік шарты бойынша іздеген нүктелердің координаталарын табайық:

уу ₁ - z - z ₁ = 0,

у + z - 1 = 0.

А ₁ В ₁ С ₁ у ₁ 1

= = , = - ,

A ₂ B ₂ C ₂ 1 1

у ₁ = - 1, х ₁ = 0, z = 1

;

уу ₁ - z - z = 0,

у - z - 1 = 0.

^___

Гиперболалық параболоид.

Тік бүрышты координаталар системасында

х ² у ²

― = 2 ₁

р q

теңдеуімен кескінделетін екінші ретті бетті гиперболалық параболоид деп атаймыз. Мұнда р > 0, q > 0 . Берілген тендеудегі х, у ағымдық координаталық екінші дәрежелі болғандықтан, бұл екінші ретті бет у z,

хz жазыктықтарына және О z апликата осіне қарағанда симметриялы болады. Екінші ретті беттің ху жазықтығымен қиылысатын сызығын анықтау үшін z-ті нольге тең деп алайык. Енді теңдеу былайша түрленеді:

х ² у ² х у х у

― = 0, + ― = 0,

2р 2q V2р V2 q V2р V2 q

х у

+ = 0,

V2р V2 q

х у

+ = 0.

V2р V2 q

Бұл теңдеулер ху жазықтығындағы екі түзуді кескіндейді, Бұл түзулер координаталардың бас нүкгесінен өтеді және Ох, Оу осьтеріне симметриялы болады. Гиперболалык параболопдка z = Һ жазықтығын жүргізсек, онда оның ху жазыктығындағы параллель қимасы гипербола болады:

х ² у ² х ² у ²

― = h, ― = 1.

2 р 2 q 2 рh 2h

Гиперболаның жарты осьтері а ₁ =V2рh, b ₁ = V 2qh. Гипербола төбелерінің арасы 2а = 2~\/2рһ. һ өскен сайын гипербола осі өсіп отырады. Бұл жағдайда гиперболалык параболокд ху жазыктығының үстінде, Ох осінің бағытымен шексізге дейін кетеді. h азапған сайын қима жазықтығы төмендей береді. z = Һ = 0 болғанда кима жазықтығы ху жазықтығымен беттеседі.

Егер екінші ретті бетті z =- Һ жазықтығымен қисақ, онда оның кимасындағы сызық тағы да гипербола болады:

х ² у ²

― = - h

2 р 2 q

немесе

х ² у ²

― = 1.

2 q h 2р h

Бұл гиперболадағы нақты жарты ось b ₁ = V 2qh, жорымал жарты ось b ₁ = V 2рh.

Екінші (II) теңдеу мен үшінші (III) теңдеудің айырмасы, олардың осьтерінін алмасатындығында.

h ескен сайын z =-h жазыктығы төмендейді. хг жазықтығы гиперболалық параболоидты х- = 2р z параболаның бойымен қияды,

яғнн егер у = 0 болса. онда у ² = 2р z болады. Егер х = 0 болса, онда у ² = - 2 q z болады.

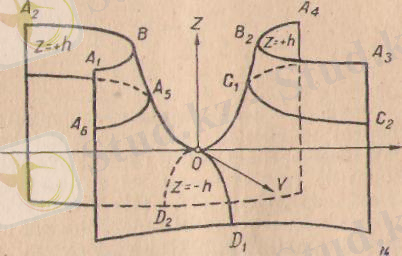
Осы шыккан корытындыларды пайдаланып гиперболалық параболсидтың графигін салуға болады 179-сызбада z =+h гипепбола

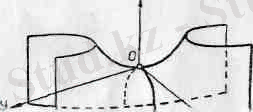
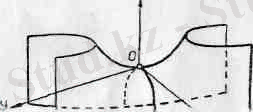
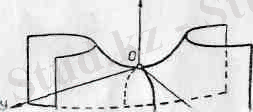
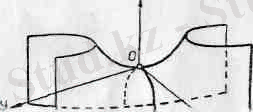
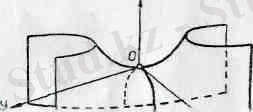
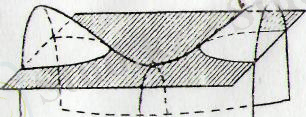
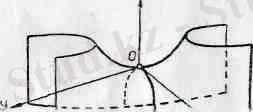
лык кисықтар. 180. а-сызбада пшерболалык параболоидка жүргізілген жазыктыктын кпмалары. ал 180, б-сызбада гиперболалық параболоидтың сырткы пішіні көрсетілген. 179-сызбадағы қималар: гиперболалар - . А ₂ В ₁ -А _1, . А ₁ . А ₅ . А ₆ . А ₄ В ₂ А ₃ , А ₃ С ₁ С ₂ ; параболалар - В ₁ ОВ ₂ , D ₁ ОD ₂ .

Гиперболалық параболоидтың түзу сызықты жасаушылары. Гиперболалық параболоидтың түзу сызықты жасаушыларының теңдеулерін шығару үшін, гиперболалық параболоидтың теңдеуін түрлендірейік:

х ² у ²

― = z ,

2р 2q

х у х у

+ ― = z.

V2р V2 q V2р V2 q

Осыдан екі теңдеулер системасын құрайық:

х у

+ = k ₁

V2р V2 q

х у 1

+ = z

V2р V2 q k ₁

х у

+ = k ₂

V2р V2 q

х у х

+ = z.

V2р V2 q k ₂

мұндағы k ₁ k ₂ ― еркінше алынған сандар ― параметірлер.

Осы теңдеулердің әрқайсысы жазықтықты кескіндейді, екі (I), (II) теңдеудің жиындылары екі түзуді береді. Бұл түзулер гиперболалық параболоидтың түзу сызықты жасаушылары деп аталады (181 және 182-сызбалар) . Осы (I), (II) теңдеулеріндегі х, у, z ағымдық координаталардың мәндері гиперболалық параболоидтың теңдеуін қанағаттандырады. Сондықтан түзу сызықты жасаушылар гиперболалық параболоидтың бетінде жатады. Бір қуысты гиперболоид сияқты гиперболалық параболоидтың әрбір нүктесінен екі

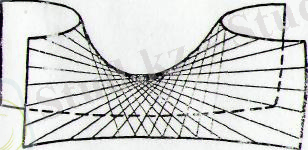
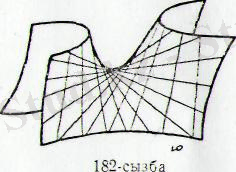
түзу сызықты жасаушылар өтеді, оның біреуі әрқашанда бірінші системадан болса, ал екіншісі әрқашанда екінші системадан болады (181 және 182-сызбалар) . Бір системаның түзулері өз ара қиылыспайды. Сейтіп, мұнда екі түрлі түзулер үйірімі болады. Бұл түзулердің біреуі бірінші системамен (I), екіншісі екінші (II) системамен кескінделеді. k ₁ және k ₂ параметрлерінің мәндеріне байланысты түзулер үйірімінің осыларға сәйкес теңдеулері шығады. Берілген есептің шарты бойынша k ₁ және k ₂ параметрлердің мәндерін табуға болады. Табылған теңдеулері арқылы гиперболалық параболоидтың түзу сызықты жасаушыларының тік бұрышты координаталар системасында қандай болып өтетінін карастыру киын емес.

Мына Зх - 2у - 4 z = 0 жазықтығында параллель болатын

х ² у ²

- - = 2 гиперболалык параболоидтың түзу сызықты

8 2

жасаушыларын табайық.

Ш е ш у і.

х ² у ² х ² у ²

― = 2 z, ― = z,

8 2 16 4

х ² у ² х ² у ²

+ ― = z.

4 2 16 4

Осыдан

х у

+ = k

4 2

х у z

- =

4 2 k

Бұл екі теңдеуді қолайлы түрге келтіру үшін әуелі оларды косайық, сонан кейін бірінен-бірін алайық. Сонда

х z х-2 k z

= k + , = ,

4 k 2 k

у у z z

+ = k - , у - k = - ,

2 2 k k

z х-2k k-у z

k - у= , = = .

k 2 1 k

Есептің шарты бойынша бұл түзу берілген Зх - 2у -4г = 0 жа-зыктығына параллель. Сондықтан

3 • 2 - 2 • 1-4• k = 0, 6-2-4 k = 0, k =1.

Гиперболалық параболоидтың түзу сызықты жасауілыларыньщ біреуінің тендеуі

Х -2 у -1 z

= = .

2 -1 k

Енді екінші теңдеуін табайық:

Осы екі теңдеуді әуелі қосайык, сонан кейін бір-бірінен алып тас-тайык. Сонда

х z х-2 l z

= L + , = ,

2 k 2 l

z z

- у= l- , y+l= ^,

l l

x-2l у+ l z

= = ,

2 1 l

Түзу мен жазықтықтың параллельдік шарты бойынша параметрін тауып, іздеген екінші жасаушы түзудің теңдеуін жазанық:

6-2-4 l = 0, l =1;

x - 2 у+ 1 z

= = .

2 1 1

Екінші ретті беттің дөңгелектік қималары.

Егер екінші ретті бетке жазықтық жүргізгенде оның қимасы шеңбер болса, онда мүндай қиманы екінші ретті беттің дөңгелектік қимасы дейміз. Екінші ретті беттің нүктелерінде жанама жазықтықтар дөңгелектік қималарға параллель болса, онда мүндай нүктелерді дөңгелену нүктелері дейміз. Ең алдымен екінші ретті беттің дөңгелектік қима-ларының теңдеулерін қорытып шығарайық. Сонан кейін дөңгелену . нүктелерінің координаталарын табатын формулаларды келтірейік.

1) Әуелі эллипсоидтың теңдеуін алайық:

x ² у ² z ²

⁺ + - 1= 0

а ² b ² с ²

Енді координаталардың бас нүктесінен ететін шардың

x ² у ² z ²

⁺ + - 1= 0

R ² R ² R ²

теңдеуін эллипсоидтың теңдеуінен алсақ, онда мынадай теңдеу шығады:

1 1 1 1 1 1

- x ² + - у ² + - z ² = 0

а ² R ² b ² R ² c ² R ²

Бұл теңдеу эллипсоид пен шардың қиылысатын сызығынан өтетін екінші ретті бетті сипаттайды. Дәлірек айтқанда, бұл теңдеу төбесі координаталардың бас нүктесінде болатын конустық бетті сипаттайды. Егер (26) теңдеудің коэффициенттерінің біреуі нольге тең болса, онда ол екі жазықтықтың теңдеулерін береді. Мысалы, а>b>с болғанда, мына коэффициент ноль болсын:

1 1

- - = 0

c ² R ²

Қойылған шарт бойынша а>b>с. Сондықтан эллипсоидтың бұл қималары жорымал болады.

1 1

- - = 0

b ² R ²

Бұл (30) жазықтықтар - эллипсоидтың ценгрінен ететін (28') жазықтыктарына параллель болатын жазықтықтар. Мұндағы u ₁ және u ₂ кез келген параметрлерді көрсетеді.

Сонымен, корыта келгенде эллипсондтың центрінен ететін дөнгелектік жазықтықтарға параллель болатын кез келген жазықтықтар эллипсоидтың деңгелектік қималары болады.

Осы жазықтықтарға параллель жазықтықтар эллипстік параболоидты шеңбердің бойымен қияды, яғни бұл теңдеулер параболоидтың дөңгелектік екі қимасын сипаттайды.

2) Дөңгелену нүктелерінің координаталарын анықтайтын формулаларды шығарайық. Эллипсойтың жанасу нүктесінің координаталары х ₁ у ₁ z ₁ болсын Онда.

хх ₁ уу ₁ z z ₁

+ + - 1= 0

а ² b ² с ²

жанама жазықтығы (28') тендеудің екі жазықтығына параллель болғандықтан, мына

x ₁ y ₁ z

: V a ² - b ² = : 0 = : ± V b ² - c ²

а b c

шарттар орындалады, яғни бұл - екі жазықтықтың параллельдік шарттары. Енді эллипсоидтың теңдеуі мен бұл теңдеулерді біріктіріп шығарайық:

х ² ₁ у ₁ ² z ² ₁

+ + - 1= 0

а ² b ² с ²

х ₁ у ₁ z ₁

- 1= 0,

а b с

V a ² - b ² 0 ± V b ² - c ²

y ₁ = 0, сонда

немесе

у ² + г ² -к ² х ² = 0,

лен айналдыратын

мұндағы к = і§ а, а - конустың жасаушысы осьтің арасындағы бұрыш (183-сызба) .

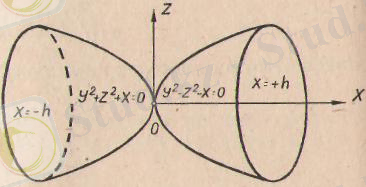
183-сызбадағы х=±һ - қиюшы жазықтар. Олар уОг жазықты-ғына параллель. Бұл конустың теңдеуі у ² + г ² - к ² х ² = 0. Ол Ох осіне және координаталардың бас нүктесіне симметриялы болады. АВ түзуін абсцисса осінен айналдырдық (183-сызба) . г і

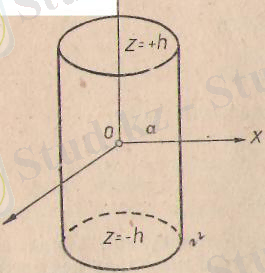
2-м ы с а л. Апликата осіне параллель у = а түзуін сол апликата осінен айналдырсақ, онда цилиндрлік бет шығады. Оның тендеуі

+ Уу ² + х ² = а, у ² + х ² = а ² ,

186-сызба 187-сызба

мұндағы а - цилиндрдің-дөңгелек қимасының радиусы (184-сызба) .

3-м ы с а л. Мына у ² = х параболаны Ох осінен айналдырсақ,

онда айналмалы параболоид шығады (185-сызба) . Оның теңдеуі:

(± У у ² + г ² ) ² = х, у ² + г ² -х = 0. Егер у ² =-х болса, онда у ² + г ² + х = 0 айналмалы параболоид шы-ғады (185-сызбаға қараңдар) .

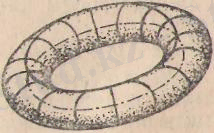
4-м ы с а л. Центрі (а, 0), радиусы і?-ге тең (х-а) ² + у ² = Я ² шең-берін Оу осінен айналдырғаннан шығатын геометриялық денені тор деп атайды (186-сызба) . Оның теңдеуі

(± Үх ² + г ² -а) ² + у ² = К. ² , х ² + у ² + г ² -Қ ² = 2аУ х ² + г ² , мүндағы К>а>0. Тор сақина тәрізді дене (187-сызба) . Бұл тор-дың әрбір қимасы дөңгелек болады (186-сызбада төрт қимасы кер-

сетілген) .

5-мысал. Мынадай х = і%г теңдеуімен берілетін сызықтық Ог

осінен айналғаннан шығатын кеңістіктік дененің теңдеуі:

±У~¥+ф = і%г,

Х ² + у ² - І£ ² 2=0,

мұнда 0 = 2<90° (188-сызба) . Жаттығулар

Мына а) х2+у2=А, ә) х2-і/2=9, б) х2++{/2+г2=1,, в) х2+у2=0теңдеулері кеқістікте қандай геометриялық бейнелерді кескіндейді?
Теңдеулер системасы берілген: