Қолданбалы математика

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 67 бет
Таңдаулыға:

Кіріспе

Болашақ информатиктер үшін қолданбалы математиканың ең маңызды саласының бірі - экономикалық есептерді компьютерде модельдеу және шешу әдістеріне арналған. Бұл пәнді оқыту студентке қарапайым экономика есептерінің математикалық модельдерін құрастыруда алғашқы қадам жасауға, олардың математикалық қойылуы мен шешу әдістерін үйренуге мүмкіншілік береді.

Бұл пән жоғары математика курсынан кейін оқылуға тиіс; бұл жерде сызықтық алгебра мен шектелген өлшемді кеңістіктегі дөңес жиындар теориясының рөлі аса маңызды. Математикалық бағдарламалауды оқу кезінде алған білімін студент мамандығы бойынша экономика саласының есептерінің экономика-математикалық модельдерін құрастыру, осыдан аланатын математикалық есептерді қою, оның алгоритмін құрастыру және есептеу техникасын пайдаланып, шешімдерін табу үшін қолданады.

Қойылу шарттарына байланысты экономикалық есептері екі түрге бөлінеді: сызықтық бағдарламалау есептері және сызықтық емес бағдарламалау есептері.

Олардың ішінде сызықтық бағдарламалау есептері жақсырақ зерттелген; олар үшін қуатты шешу тәсілдері мен ЭЕМ үшін құрастырылған қолданбалы бағдарламалар пакеттері бар. Осыған байланысты көпшілік жағдайда сызықтық есептер қарастырылып, экономика есептерінің математикалық модельдерін сызықтық бағдарламалау есебіне келтіруге тырысады. Сызықтық емес бағдарламалау есептерін шешу тәсілдері де бар; бірақ олардың өзіне тән қиыншылықтары болғандықтан оған сәйкес модельдер әзірше азырақ қолданылуда.

Экономикалық математикалық модельдеу ғылым саласы және оқу пәні ретінде кейінірек пайда болған; күрделі экономика есептерін шешу қажеттілігі, үйлесімді шешімдер жиынынан ең тиімдісін (оптималь) таңдау және басқалар математика мен есептеу техникасын экономика саласына енгізуге себепші болды. Бұл операциялық зерттеудің пайда болуына әкелді.

Қазіргі кезде көптеген оқулықтар, оқу құралдары және басқа да әдебиеттер жарық көруде. Бірақ олардың ішінде қарапайым есеп жинақтары өте аз және республика кітапханаларында жоқтың қасы деуге болады. Бұл пәннің есептерін шешуге арналған қазақ тілінде оқу құралдары мүлдем жоқ.

Осыған байланысты осы оқу құралы ұсынылып отыр. Ол экономика және информатика мамандықтарында оқитын студеттер мен жоғарыда аталған мәселелер туралы білім алғысы және практикалық есептерді шешуге машықтанғысы келетіндерге арналған.

2. Векторлар, матрицалар және анықтауыштар

Реттелген n нақты сандар жүйесін n өлшемді вектор деп атайды; ол былайша белгіленеді:

Х=(x _1, x _{2, . . .} x _n ),

Мұндағы x ₁ x _{2 . . .} x _n вектордың компоненттері немесе құрастырушылары деп аталады. Векторлар бас әріптермен, ал компоненттері кіші әріптермен белгіленеді.

Екі вектор Х және Ү бір-біріне тең деп есептелінеді, егер олардың сәйкес компоненттері бірдей болса, немесе x1=y1, і=1, 2, . . . , n
Х және Ү векторларының қосындысы деп Ζ векторын атаймыз, егер оның компоненттері былайша анықталса :

z _i =x _i +y _i , і=1, 2, …. ., n

4. Қос Х және Ү векторларының айырмасы деп келесі Ζ векторын айтамыз:

Ζ=Х-Ү=(x ₁ -y ₁ , x ₂ -y ₂ , …, x _n -y _n )

5. Барлық компоненттері нөлге тең векторды нөлдік вектор деп

атайды:

o=(o, o, …. o)

Х векторының а нақты санына көбейтіндісі деп келесі векторды атайды:

a∙Х=(ax _1, ax ₂ , …, ax _n )

Қосу, алу және санға көбейту тәртібі енгізілген n өлшемді барлық векторлардың жиынын n өлшемді векторлық кеңістік деп атайды.
Егер n = 3 болса, онда векторлық кеңістік қарапайым үш өлшемді кеңістік болып табылады.
Х және Ү екі векторының скалярлық көбейтіндісі деп келесі санды атайды:

S=(Х, Ү) =
\[\sum_{i=1}^{t}\tilde{O}_{i}\tilde{O}_{j}\tilde{O}_{j}\]

Екі Х және Ү векторлары ортогональды деп аталады:

(Х, Ү) =0

Х векторының ұзындығы(нормасы) деп келесі санды атайды:

\[\left|\widetilde O\right|\ --\sqrt{{\chi_{1}^{2}}+{{{\chi_{2}^{2}}}+........+{{\chi_{n}^{2}}}}}\]

Скалярлық көбейтінді туралы түсінік (немесе метрика) енгізілген n өлшемді векторлық кеңістік Эвклид кеңістігі деп аталып, Еnдеп белгіленеді.
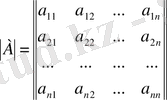
Тіктөртбұрышты сандар кестесі

матрица деп аталады. Ол мұнда n жатық жол мен m тік жолдан тұрады. Матрицаны құрайтын сандар оның элементтері деп аталады. Оның бірінші индексі жатық жол, ал екіншісі тік жол нөмірін көрсетеді.

Кейде матрица былайша белгіленеді:

A=(A ₁ , A ₂ , …, A _m ),

мұндағы A _j -j-ші тік жол немесе вектор - тік жол:

A _j =

Егер n=m болса, онда А матрицасы квадрат матрица деп аталады.

а _іі , і=1, 2, . . . , n, элементтері А матрицасының бас диагоналін құрайды .

А және В матрицаларының қосындысы (айырмасы) деп элементтері келесі формула бойынша анықталатын С матрицасын атайды:

C=A
\[\frac{1}{1-}\]

\[\frac{1}{1-}\]
B, c _ij =a _ij
\[\frac{1}{1-}\]
b _ij , i=1, 2, …, n; j=1, 2, …, m

А матрицасының с санына көбейтіндісі деп келесі В матрицасын атайды:

B=c∙A, b _ij =c∙a _ij , i=
\[\overline{{}}\]
, j=
\[\overline{{1,\partial\theta}}\]

А матрицасының с вектор-тік жолға көбейтіндісі деп компоненттері келесі формуламен анықталатын В векторын атайды:

B=A∙C, b _i =
\[\sum_{j=1}^{m}a_{i j}b_{j},\]
i=
\[\overline{{}}\]

А матрицасының В матрицасына көбейтіндісі келесі формула бойынша анықталатын С матрицасын атайды.

C=A∙B, c _ij =
\[\sum_{k=1}^{l}a_{i k}b_{k j},i=\overline{{{1,i}}}\,,j=\overline{{{1,\partial}}}\,.\]

Көбейту амалын орындау үшін бірінші матрицаның тік жол саны екіншісінің жатық жол санына тең болуы тиіс.

Транспонирленген матрица Атдеп жатық жол ретінде алғашқы А матрицасының оған сәйкес тік жолы болатын матрицаны атайды:

Квадрат А матрицасын қарастырайық. А матрицасына сәйкес n-ші дәрежелі анықтауыш деп келесі тәртіппен құрастырылған n! мүшелердің қосындысын атаймыз: әрбір мүше матрицаның n элементінің көбейтіндісі ретінде, әр жатық жолынан және тік жолынан бір элементтен алынған; ал оның таңбасы индекстерге байланысты егер олар жұп болса, онда оң, ал керісінше жағдайда -теріс болады. Анықтауыш келесі түрде жазылады:

Транспонирлеу кезінде матрица анықтаушы өзгермейді:

\[|{\hat{A}}|=|A^{T}|\]

Егер анықтауыштың бір жолы нөлдерден тұрса, онда ол нөлге тең болады.
Екі жодың орынын ауыстыру кезінде анықтауыштың абсолют мәні өзгермей, таңбасы ғана өзгереді.
Екі жолы бірдей анықтауыш нөлге тең болады.
Егер бір жолдың барлық элементін С деген санға көбейтсек, онда анықтауыштың өзі де сол С санына көбейтіледі .
Егер анықтауыштың бір жолына екінші жолды кез келген санға көбейтіп қосқанда анықтауыштың мәні өзгермейді.
Бір -біріне пропорциональ екі жолы бар анықтауыш нөлге тең болады.
Егер бір жолы басқа жолдардың сызықтық комбинациясы болса, онда ол анықтауыш нөлге тең болады. Анықтауыштың і-ші жолы басқаларының сызықтық комбинациясы болуы үшін барлығы нөлге тең емессандары табылып, келесі шарт орындалуыға тиіс:

a _ij =
\[\sum_{s=1}^{n}k_{s}a_{s j},s\ \ne j^{s}\]

Бүтін санkқарастырылсын: 1≤k≤n-1, және анықтауыштаkтік жол менkжатық жол таңдалынсын. Осы тік және жатық жолдардың қиылысына орналасқан элементтерkдәрежелі матрицаны құрайды. Осы матрица анықтауышы к-ші дәрежелі минор деп аталады .
Берілген А матрицасының аijэлементі орналасқан жатық және тік жол сызып тасталынсын. Қалған элементтерден n-1 -ші дәрежелі матрица құралады; оның анықтауышы Мijдеп белгіленсін. Cонда А матрицасының аijэлементінің алгебралық қосымшасы деп келесі санды атайды:

A _ij =(-1) ^i+j ∙M _ij

Квадрат матрица ерекше деп аталады, егер оның анықтауышы нөлге тең болса, ал керісінше жағдайда ерекше емес деп аталады.
А-1матрицасы А матрицасының кері матрицасы деп аталады,

егер A ^-1 ∙A=E

Мұндағы Е -n-ші дәрежелі бірлік матрица:

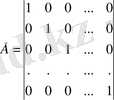
Кері матирца A ^-1 былайша анықталады:

A ^-1 =

мұндағы
\[\left|A\right|\]
анықтауыш, A _ij алгебралық қосымшалар

n - өлшемді А1, А2, . . . , Аsвекторлар берілсін. Онда вектор

k ₁ ∙ A ₁ + k ₂ ∙ A ₂ + … + k _s ∙ A _s

берілген векторлардың сызықтық комбинациясы деп аталады. А ₁ , А _2, . . . , А _s векторлар жүйесі сызықтық байланыста деп есептелінеді, егер нөлдік вектор олардың сызықтық комбинациясы болып және к ₁ , к _2, . . . , к _s коэффициеннетрінің ішінде нөлге тең еместері болса. Керісінше жағдайда бұл векторлар жүйесі сызықтық байланыссыз деп аталады, немесе мына шарт

\[{\frac{\hat{\sum}}{\partial t}}k_{i}A_{i}=0\]

тек келесі жағдайда мүмкін:

k ₁ =k ₂ =…. =k _s =0

Нөлге тең емес минорлардың ең үлкен дәрежесі матрицанын рангысы деп аталады.

2. 1. Сызықтық теңдеулер жүйелері

1. Сызықтық теңдеулер жүйесінің жалпы түрі:

\[\sum_{j=1}^{n}a_{1j}x_{j}=b_{1},i=1,2,...,m;\]
(1. 1)

ол n белгісізі бар m теңдеуден тұрады: оның коэффиценттері жүйенің матрицасын құрайды:

\[A=\left\|a_{1j}\right\|,i=1,m;j=1,n.\]

ал вектор

B=(b _1, b ₂ …, b _n ) ^T

Жүйенің бос мүшелерінің тік жолы деп аталады.

Теңдеулер жүйесін келесі түрлерде де жазуға болады:

\[\sum_{j=1}^{n}A_{1j}X_{\,j}=B\ A^{*\star}X=B,\]

Мұндағы

X=(x _1, x ₂ …, x _n ) ^T

Белгісіздер тік жолы деп аталады.

2. Берілген жүйенің кеңейтілген матрицасы деп келесі матрицаны атаймыз:

\[\overline{{\underline{{A}}}}\]
=(A ₁ , A ₂ …., A _n, B)

3. Егер теңдеулер жүйесін қанағаттандыратын X ₁ (1=1, n) мәндері табылса, онда келесі векторды соның шешуі деп атайды:

\[X=(\overline{{{X}}}_{1},\overline{{{X}}}_{2},...\overline{{{X}}}_{n})\]

Ең болмағанда бір шешімі болатын сызықтық теңдулер жүйесін үйлесімді, ал керісінше жағдайда үйлесімсіз деп атайды.
Сызықтық теңдеулер жүйесі үйлесімді болуы үшін оның матрицасынан рангысы кеңейтілген матрица рангысына тең болуы керек.
Жордан- Гаусс әдісі

Бұл әдісті пайдалану үшін теңдеулер жүйесін келесі түрде жазайық:

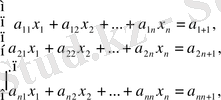
Бұл жүйені шешу процесі n қадамнан тұрады. Кез-келген к-ші қадамда к-ші теңдеудегі х _к белгісізінің коэффиценті нолге тең емес деп, теңдеулер жүйесінің коэффиценттерімен келесі формулалар бойынша өзгертіледі:

\[a_{k j}^{\mathrm{\scriptsize~(k)}}=\frac{{}^{a}k j^{\left(k-1\right)}}{{}^{\left(k-1\right)}},j=1,2,...,n+1;\]

(1. 3)

\[a_{i j}^{(k)}=a_{i j}^{(k-1)}-a_{i k}^{(k-1)}.a_{k j}^{(k)}\]

(1. 4)

\[\begin{array}{c}{{j=1,2,...,n+1;}}\\ {{i=1,2,...,n;(1~~k)}}\\ {{k=1,2,...,n.}}\end{array}\]

Бұл формулалар Жордан-Гаусс формулалары деп аталады және олар кейінірек, Симплекс тәсілінің алгоритмін қарастыру кезінде қолданылады.

2. 2. Дөнес жиындар туралы.

1. Гипержазықтық деп келесі сызықтық теңдеуді қанағаттандыратын n өлшемді кеңістіктіктегі нүктелер жиынын атаймыз:

\[a_{1}x_{1}+a_{2}x_{2}+...+a_{n}x_{n}=b,\]

мұндағы

\[A=\left(Q_{1},a_{2},....,Q_{n}\right)\ \ne\!0\]

2. Гипержазықтық жарты кеңістік деп аталынатын екі жиынды туғызады:

\[{\cal Q}_{1}X_{1}+{\cal Q}_{2}X_{2}\,+\,.....{\cal Q}_{n}X_{n}\,\,\,\,\le\cal D\]

және

\[{\cal Q}_{1}X_{1}+{\cal Q}_{2}X_{2}\,+\,.....{\cal Q}_{n}X_{n}\,\,\geq\bar{\cal D}\]

3. В _n кеңістігіндегі кез-келген түзудің теңдеуі келесі түрде жазылады.

X=A+Bt,

\[<\stackrel{\ V}{\downarrow2}\mathrm{~}\int\mathrm{~}t\mathrm{D}\sim\]

Equation. 3

Мұндағы А және В -векторлар: В -бағыттаушы вектор деп аталады.

Егер t параметрі төменнен немесе жоғарыдан нақты санмен шектелген болса, онда оған сәйкес жиынды бағыттаушы векторы В сәуле деп атайды.

Егер t екі жағынан шектелген болса, онда ол жиын кесінді деп аталады.

4. Кесіндінің кез келген х нүктесін оның ұштарынан А А сызықтық комбинациясы ретінде қарастыруға болады.

\[A\bar{\phi}=A+B\cdot\,a\ ,A\bar{\phi}=A+B\cdot\,\bar{\beta}\]

Шын мәнінде

\[A+B\cdot\ t=m_{1}(A+B\cdot\ a\ )+m_{1}(A+B\cdot\beta)\]

\[m_{1}=\frac{b\,-\,t}{b\,-\,a},m_{2}=\frac{t-a}{b\,-\,a}\]

Ескертетін жай

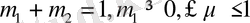
Сонымен, ұштары А және А болатын кесінді келесі түрдегі х нүктелерінің жиыны болады:

5. С жиынынын әрбір х нүктесіне Р(х) нақты санын сәйкес келтіретін Ғ(х) функциясы делік. Онда С жиыны Ғ(х) фукциясының анықталу облысы немесе онын берілу облысы деп аталады.

6. Егер кез келген екі А және В нүктелерн қосатын кесінді толығымен G жиынына жататын болса, онда оны жыйн деп аталады:

\[m4+(1-\ \mu)\cdot B\]

\[0\leq\mu\ \leq1\]

Егер n өлшемді кеіңстікте сызықтық теңсіздіктер жүйесі қарастырылса:

\[a_{i1}x_{1}+a_{i2}x_{2}+....+a_{i n}x_{n}\le b_{i},i=\overline{{{1,m}}}\]

\[a_{i1}x_{1}+a_{i2}x_{2}\ {\le}b_{i},i=\overline{{{1,m}}}\]

Онда ол дөңес көпжақ құрайды, себебі ол теңсіздіктердің әр қайсысы жарты кеіңстікті анықтайды. Ескертетің жәй - ол көпжақ облыс болуы да мүмкін.

Екі өлшемді кеіңістікті немесе жазықтықтағы жағдайды қарастырайық:

Онда ІІІ шартты жазықтықтың қиылысы көпбұрыш құрайтыны көруге болады.

(№ 26 есепті қараңыз) .

3. 1. ҚАРАПАЙЫМ ЭКОНОМИКА ЕСЕПТЕРІНІҢ МАТЕМАТИКАЛЫҚ

МОДЕЛЬДЕРІН ҚҰРАСТЫРУ

Кез келген ғылым саласында есептеу техникасы мен математикалық зерттеу тәсілдерін қолдану үшін (мысалы, эканомикада) алдымен зерттелінетін құбылыстың математикалық моделін құрастыру қажет.

Математикалық модель деп есептің мақсаты мен шарттарына сәйкес құрастырылған оның негізгі параметірлерін байланыстыратын математикалық формулалардың (теңдеулер, теңсіздіктер, интегралдар және т. б. ) жиынын айтамыз. Математикалық модель математикалық есепті құрастыруға мүмкіншілік жасайды.

Есептің математикалық моделі қандай болуы тиіс ? - деген сұрақ тууы мүмкін.

Бұл жерде ол туралы екі түрлі көзқарасты қарастырайық. Кез келген қарапайым есептің өзі көптеген факторларға байланысты болады; ал олардың тек белгілі біреулері ғана есепке алынуы мүмкін. Кейде, барынша көп фактордың құбылысқа тигізетін әсерін анықтауға мүмкіншілік бермейтін есепке келтірілуі мүмкін. Екіншіден, көпшілік факторларды есепке алмау математикалық есепті оңайлатқанмен оның шешімінде ешқандай мағына болмайтын жағдайға келтірілуі мүмкін. Сондықтан кез келген құбылысты зерттеу ісінің табысты болуы оның математикалық моделін сәтті құрастыруға байланысты.

Енді әртүрлі қарпайым экономика есептерінің математикалық моделін қарастырайық.

Төменде қарастырылған есептердің барлығына тән қасиет берілген шартар бойынша теңдеу немесе теңсіздіктер күйінде жазылған шектеулер мен есепті шешудің критерийін (белгісін) анықтайтын мақсат функциясы құрастырылады. Бұл жерде критерийі мақсат фукциясының экстремаль (maximum немесе minimum) мәндерін табуға арналған математикалық бағдармалау есептері қарастырылады; олар вариациялық есептер класына жатады.

№І. (Өндірісті жоспарлау туралы есеп)

белгілі бір кәсіпорын n түрлі бұйым А ₁ , А ₂ . . . А _n шығару үшін m түрлі шикізат В ₁ , В ₂ . . . В _m пайдаланады. Кәсіпорын қоймасындағы шикізат қоры әрбір бұйымға жұмсалынатын шикізат мөлшері мен дайын бұйымнан түсетін пайда келесі кестеде көрсетілген:

Бұйым түрі

Жұмсалатын шикізат мөлшері

Пайда

Жоспар

B ₁

B ₂

B _j

B _m

Бұйым түрі: A ₁

Жұмсалатын шикізат мөлшері: a ₁₁

Пайда: a ₁₂

Жоспар:

a _1j

a _1m

c ₁

x ₁

Бұйым түрі: A ₂

Жұмсалатын шикізат мөлшері: a ₂₁

Пайда: a ₂₂

Жоспар:

a _2j

a _2m

c ₂

x ₂

Бұйым түрі: A ₃

Жұмсалатын шикізат мөлшері: a ₁₁

Пайда: a ₁₂

Жоспар:

a _1j

a _1m

c ₁

X ₁

Бұйым түрі: A _n

Жұмсалатын шикізат мөлшері: a _n1

Пайда: a _n2

Жоспар:

a _nj

a _nm

c _n

x _n

Бұйым түрі: Шикізат қоры

Жұмсалатын шикізат мөлшері: b ₁

Пайда: b ₂

Жоспар:

b _j

b _m

\[F=\sum_{i=1}^{n}C_{i}X_{i}\]

Іске асырылғанда өте көп пайда беретін өндіріс жоспарын жасау керек.

Шешуі: Алдымен әрбір шығарылатын А бұйымның мөлшерін белгілейміз. Онда түсетін жалпы пайда мөлшері келесі формула бойынша анықталады:

F=c ₁ x ₁ + c ₂ x ₂ +…. +c _n x _n (2. 1)

Сонымен бірге жұмсалатын әрбір шикізат оның қоймадағы қорынан аспауға тиіс:

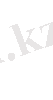
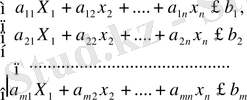(2. 2)

ал бұйым мөлшері теріс мән қабылдай алмайды:

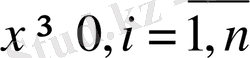(2. 3)

Қарастырылып отырған есептің математикалық модельі (2, 1), (2, 2), (2, 3) формулалары арқылы анықталады. Осыдан келесі математикалық есепті қоюға болады: (2. 2) мен (2. 3) теңсіздіктерін қанағаттандыратын Ғ(х) фук

№2 (Азық құрамы туралы есеп)

Айталық n түрлі азық-түлік А ₁ А _{2 . . .} А _п болсын делік олардың бірліктерінің құны С ₁ С _{2 . . .} С _п белгілі. Әрбір азық-түлікте түрлі В ₁ В ₂ В _т пайдалы заттары (белок, май, көмірсутегі, витаминдер және т. б. ) болатындығын ескеріп, азық құрамын жасау керек: ондағы пайдалы заттардың әрқайсысы В ₁ В ₂ В _n -нен кем мөлшерде болмауға тиіс.

Осындай шарттарды қанағаттандыратын және жалпы құны ең арзан болатын азық құрамын жасау керек.

Пайдалы заттардың әрбір азық-түліктегі мөлшері төмендегі кестеде көрсетілген.

Азық түлік

Пайдалы заттар

Құны

Мөлшері

В ₁

В ₂

. . .

В _j

. . .

В _m

Азық түлік:

A ₁

A ₂

. . .

A ₁

. . .

A _n

Пайдалы заттар:

a ₁₁

a ₂₁

…

a _{і 1}

…

a _n1

Құны:

a ₁₂

a ₂₂

…

a _{і 2}

…

a _{n 2}

Мөлшері:

. . .

a _1j

a _2j

. . .

a _іj

. . .

a _nj

. . .

a _1m

a _2m

…

a _іm

…

a _nm

C ₁

C ₂

…

C _і

…

C _n

X ₁

Х ₂

. . .

Х _і

. . .

Х _n

Азық түлік: Қажетті мөлшер

Пайдалы заттар: b ₁

Құны: b ₂

Мөлшері: …

b _j

…

b _m

F=∑ C ₁ X ₁

¹⁼¹

Шешуі:

Азық құрамына кіретін азық-түлік түрлерінің мөлшерін х _1, 1=1, n деп белгілейік. Сонда жалпы жұмсалынатын қаржы келесі формуламен анықталады:

F=C ₁ X ₁ +C ₂ X ₂ + . . . C _n X _n (2. 4)

Есептің шарты бойынша азық құрамындағы пайдалы заттар көрсетілген мөлшерден кем болмауы тиіс:

a ₁₁ x ₁ + a ₁₂ x ₂ + . . . + a _1n x _n ≥b ₁

a ₂₁ x ₁ + a ₂₂ x ₂ + . . . + a _2n x _n ≥b ₂

. .

a _m1 x ₁ + a _m2 x ₂ + . . . + a _mn x _n ≥b _m (2. 5)

aл азық-түлік мөлшері теріс мән қабылдай алмайды:

х _і ≥0, і =1, n (2. 6)

Сонымен, қарастырылған есептің математикалық моделі (2. 4) -(2. 6) формулаларымен анықталады. Мұнда келесі математикалық есепті қоюға болады:

(2. 5) және (2. 6) теңсіздіктерді қанағаттандыратын әрі (2. 4) функциясының минимумына сәйкес келетін белгісіздер Х ₁ Х ₂ … Х _n -нің мәндерін табу керек.

Мұндағы Р(х) -мақсат фунуциясы ал (2. 5) (2. 6) теңсіздіктері шектемелер деп аталады. Есептің критерийі -оның мақсат функциясының минимумы.

№ 3. (Тапсырманы кәсіпорындарға бөлу туралы есеп)

Өндіріс саласының жоспары бойынша белгілі бір т уақытта А ₁ бұйымынан М ₁ дана (1-1, n) шығарылуғатиіс. Бұл бұйымдар т кәсіпорындарында шығарылады, бірақ бір кәсіпорын бір кезеңде бірнеше түрлі бұйымды қатарынан шығара алмайды. Сонымен бірге a _1j -ші кәсіпорын уақыт бірлігінде шығаратын А ₁ бұйымының саны мен b _1j -осы А ₁ бұйымының біреуінің құны белгілі. Шығарылатын барлық өнімнің құны аз болатындай етіп тапсырманы кәсіпорындарға бөлу жоспарын жасау керек.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.