Жоғары дәрежелі алгебралық теңдеулерді нақты сандар өрісінде шешудің интервалдық-теоремалық әдісі


Ќ. А. Ясауи атындаѓы Халыќаралыќ
Ќазаќ-Т‰рік Университеті
Саттарханова Жанар Нұржанызы
Жаратылыстану факультетініњ 2
 -курс
-курс
ЖМА-711 тобыныњ студенті
Жоғары дәрежелі алгебралық теңдеудің нақты сандар өрісінде шешу әдістерінің бірі
Т‰ркістан -2009 г
Мазмұны
КІРІСПЕ. . 3
§1. Жоғары дәрежелі алгебралық теңдеуді нақты сандар өрісінде шешу 4
§2. Алынған әдісі пайдаланып теңдеулерді шешу. . 11
Қорытынды25
Әдебиеттер. . 26
КІРІСПЕ
Үшінші және төртінші дәрежелері теңдеулерді шешу XVI ғ. алынғаны белгілі. 1629ж Альфер де Жирар келесі ұйғарымды тұжырымдаған болатын: Комплекс коэффициентті n дәрежелері көпмүшеліктің n түбірі бар болады (еселік түбірлерін есептегенде) . Бұл ұйғарым «алгебраның негізгі теоремасы» деген атауға ие болды. Бұл теореманы алғаш дәлелдердің қажеттігін Даласебер айқындап, өз дәлелдеуін ұсынған (1746ж) . Бұл теорема дәлелдеуін Эйлер (1746ж), Фонсене (1759ж) және Лагранж (1771ж) ұсынған болатын. Алгебраның негізгі теоремасын дәлелдеуінің үш нұсқасын Гаусс ұсынды (1799ж., 1815ж., 1816ж. ) . Дәлелдеудің ең соңғы нұсқасын 1845ж ұсынған болатын. Осы кезеңдерде дәрежесі бес және одан жоғары теңдеулерді шешу формулаларын табудың зерттеу жұмыстары жалғасып жатты. Бұл ізденістер XIXғ басына дейін жалғасы деуге болады. Нәтижесінде төмендегідей тамаша нәтиже алынды: Дәрежесі бес немесе одан жоғары, кез-келген n үшін, n -дәрежелі кез-келген теңдеудің түбірлерін, оның коэффициенттері арқылы радикал көмегімен шешетін формуланы көрсетуге болмайды. Дәрежесі n≥5 болатын теңдеудің радикалдар арқылы жазылған жалпы формуласының мүмкін екендігін Абель (1802-1829) өз жұмыстарында көрсетті. Э. Галуа (1811-1832) өз зерттеулерінде, теңдеудің радикалдар арқылы шешілу мүмкіндіктерінің шарттарын көрсетті [1] . Теңдеулер шешімділігін зерттеу жұмыстары Э. Галуаның группалар теориясында қарастырылған. Группа түсінігі және осы негізде жүргізілген зерттеулер теңдеулердің радикалдар арқылы шешімділігі мәселесіне толығымен жақсы береді. Дәрежесі n≥5 болатын теңдеулердің түбірлерін радикалдар арқылы шешудің жалпы формуласының жоқтығы, теңдеулердің шешудің жуықтап шешу әдістерімен толығады. Жуықтап шешу әдістері кейбір жағдайлары ыңғайлы да.
Үшінші дәрежелі теңдеулерді шешудің Кардано формуласы, төртінші дәрежелі теңдеулерді шешудің Феррарт әдістері бар [2] .
Жоғары дәрежелі теңдеулерді шешуде көптеген дербес әдістер пайдаланылады. Мысалы, Р(х) =0 теңдеуін қарастырсақ, Р(х) көпмүшелігін көбейткіштерге жіктеу арқылы шешу, қайтармалы теңдеулерді шешу әдістері т. б.
Теңдеудің нақты түбірлерін анықтау үшін Штурм теоремалары, Ньютон ережесі, Декарттың таңбалар ережесі т. б қолданылады. Сондай-ақ теңдеуді шешудің жуық әдістері бар: Хорда әдісі, Ньютен әдісі, Итсрация әдісі, Лобачевский әдісі т. б. [3] .
Сондықтан, алгебралық теңдеуді шешудің қандайда бір әдістерін табу, қызығушылық туғызады. Ұсынылып отырған жұмыстағы, алгебралық теңдеудің нақты сандар өрісінде шешімділігін анықтау мәселесі көкейтесті деп есптеуге болады.
Жұмыста кез-келген дәрежелі алгебралық теңдеуді шешудің мүмкін бір әдісі ұсынылып отыр.
Практикалық маңыздылығы жұмыста ұсынылған әдістері математиканы тереңдетіп оқытатын кластарда, сыныптан тыс жұмыстарда, сондай-ақ студенттердің математикалық үйірмелерінде пайдалануға болады.
§1. Алгебралық теңдеудің нақты сандар өрісінде шешу
әдістерінің бірі
Алгебралық теңдеудің алайқ:
 А
0
х
n
+ A
1
х
n-1
+ A
2
х
n-2
+ …+A
n-1
х + A
n
= 0
(1)
А
0
х
n
+ A
1
х
n-1
+ A
2
х
n-2
+ …+A
n-1
х + A
n
= 0
(1)
Бұл теңдеуді А
0
 Equation. 3 0 бөлсек, онда
Equation. 3 0 бөлсек, онда
х n + а 1 х n-1 + а 2 х n-2 + …+а n-1 х+а n = 0 (2)
мунда а i =A i / A 0 i=1, 2, …, n.
Егер m саны (2) теңдеудің түбірі болса, онда
m n + a 1 m n-1 +a 2 m n-2 + …+a n = 0 (3)
Соңғы теңдеуді түрлендірейік:
а n-1 m+ а n =-m 2 (m n-2 + а 1 m n-3 + а 2 m n-4 +…+ а n-2 ) (4)
а
n-1
(m+
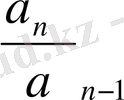 ) =- m
n
(m
n-2
+a
1
m
n-3
+a
2
m-4
+…+a
n-2
)
(5)
) =- m
n
(m
n-2
+a
1
m
n-3
+a
2
m-4
+…+a
n-2
)
(5)
Бұдан
 (6)
(6)
Белгілеу енгізейік:
 p
=
p
=
 ,
q
=
-
,
q
=
-
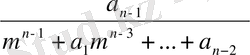 Equation. 3 (7)
Equation. 3 (7)
Біз m саны (2) теңдеудің түбірі деп ұйғарып (6) теңдігі алдық. Керісінше, егер (6) шарт орындалсы, онда m саны (2) теңдеудің түбірі болады. Сондықтан, алынған нәтижені, төменгі теорема түрінде тұжырымдауға болады.
Теорема 1. Егер m саны х n +a 1 x n-2 +…a n =0 теңдеуінің түбірі болса, онда p = q, мунда
p =
, q = -
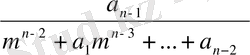
Егер p = q, онда m саны теңдеуінің түбірі.
Бу p мен q -дың мәндерін есептейтін болсақ, мынадай жағдайлар болуы мүмкін:
1)
2)
(8)
Бұл системалардың шешімдерінен
x n +a 1 x n-1 +a 2 x n-2 +…+a n =0
теңдеусінің түбірлері орналасқан интервалдар анықталанады.
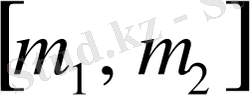 интервалын қарастырайық.
интервалын қарастырайық.
Егер х=m 1 болса, онда
p
=
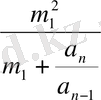 ,
q
=
-
,
q
=
-
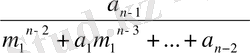 (9)
(9)
Егер х=m 2 болса, онда
p
=
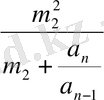 ,
q
=
-
,
q
=
-
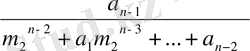
Мынадай функция құрайық:
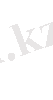
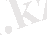
 ƒ(m) =
ƒ(m) =
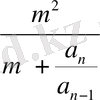 -
-
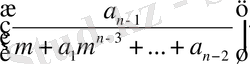 Equation. 3
Equation. 3
Бұл функцияның m 1 және m 2 -дегі мәндерін есептеп, мынадай жағдайы болуы мүмкін.
1) Δ ƒ(m 1 ) >0, Δ ƒ(m 2 ) <0
2) Δ ƒ(m 1 ) >0, Δ ƒ(m 2 ) >0
3) Δ ƒ(m 1 ) <0, Δ ƒ(m 2 ) <0 (10)
4) Δ ƒ(m 1 ) <0, Δ ƒ(m 2 ) >0
Коши теоремасын еске түсірейік. Теорема: Егер ƒ(х) функциясы
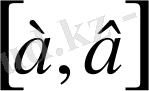 кейіндісінде үздіксіз болып және
ƒ(а) >0,
ƒ(в) <0
(немесе
ƒ(а) <0,
Δ
ƒ(в) >0
) болса, онда
х
0
кейіндісінде үздіксіз болып және
ƒ(а) >0,
ƒ(в) <0
(немесе
ƒ(а) <0,
Δ
ƒ(в) >0
) болса, онда
х
0

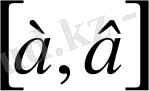 нүктесі табылып,
ƒ(х
0
) =0
болады.
нүктесі табылып,
ƒ(х
0
) =0
болады.
Коши теоремасы бойынша
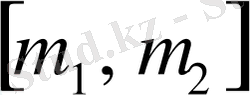 интервалда функция Δ
ƒ(m)
таңбасын ауыстырса, онда функция осы
интервалда функция Δ
ƒ(m)
таңбасын ауыстырса, онда функция осы
 аралығында ноль мәнін қабылдайды
аралығында ноль мәнін қабылдайды
 нәтижелерді төменгі теорема түрінде тұжырымдауға болады:
нәтижелерді төменгі теорема түрінде тұжырымдауға болады:
Теорема 2. Егер m келесі теңсіздіктер системасының бірін қанағаттандырса
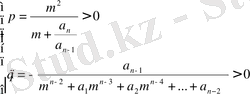 (11)
(11)
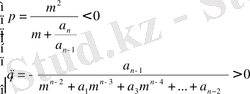 (12)
(12)
мунда
m+
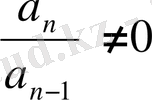 , m
n-2
+a
1
m
n-3
+…+a
n-2
, m
n-2
+a
1
m
n-3
+…+a
n-2
 0
0
және
m
 Equation. 3 [m
1,
m
2
]
интервалында Δ
ƒ(m
1
),
Δ
ƒ(m
1
)
таңбаларын ауыстырса, онда
х
n
+a
1
х
n-1
+a
2
х
n-2
+a
n
=0
тендеуші
[m
1,
m
2
]
интервалда түбірі бар болады.
Equation. 3 [m
1,
m
2
]
интервалында Δ
ƒ(m
1
),
Δ
ƒ(m
1
)
таңбаларын ауыстырса, онда
х
n
+a
1
х
n-1
+a
2
х
n-2
+a
n
=0
тендеуші
[m
1,
m
2
]
интервалда түбірі бар болады.
Элементар түрленділерді қолдана отырып, нәтижелері Теорема 1, Теорема 2 арқылы тұжырымдалған нәтижені кез-келген алгебралық теңдеуді шешуге қолдануға болады. Теорема 1, Теорема 2 қолданып х n +a 1 х n-1 +a 2 х n-2 + a n =0 теңдеуінің түбірлері орналасқан [m 1, m 2 ] интервалын анықтауға және осы аралықта жататын теңдеудің түбірін табуға болады.
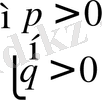 және
және
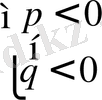 (13)
(13)
Жүйелерін шешу арқылы, өңдеу түбірлері жататын интервалдар анықталынады. Осы интевалда р(m), q(m) әртүрлі таңбалы болса, онда бұл интервалда теңдеу түбірі болмайды. Егер Δ ƒ(m 1 ), Δ ƒ(m 1 ) таңбаларын өзгертсе, осы интервалдар р мен q -дың таңбалары бірдей болса теңдеудің түбірлері бар болады.
Алынған нәтижелерді алгебралық теңдеулерді шешуге қалай қолданылатындығы төменде қарастырылады.
Үшінші дәрежелі алгебралық теңдеуді қарастырайық:
х
3
+a
1
х
2
+ a х+a
3
=0,
мунда
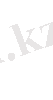 a
2
a
2
 0, a
3
0, a
3
 0,
0,
Бұл теңдеу үшін
p
=
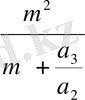 ,
q
=
,
q
=
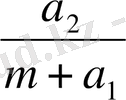 (14)
(14)
Енді түрлендірген төмендегі форманы табайық:
p
1
=
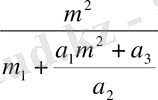 ,
q
=
-
,
q
=
-
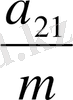 (15)
(15)
х 3 +a 1 х 2 +a 2 х+a 3 =0 теңдеуінің түбірлері орналасқан облыстарды анықтайық.
Төмендегі теңсіздіктер системасын құрасыз.
1)
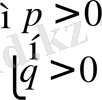 2)
2)
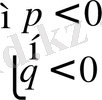 (16)
(16)
3)
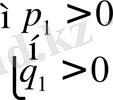 4)
4)
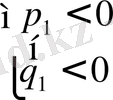 (17)
(17)
Осы теңдеулер жүйесі х 3 +a 1 х 2 +a 2 х+a 3 =0 теңдеуінің түбірлері орналасқан интервалдарды табуға мүмкіндік береді. Одан кейін теорема 2-ні пайдаланып х 3 +a 1 х 2 +a 2 х+a 3 =0 теңдеуінің түбірі анықталынады.
§2. Алынған әдісі пайдаланып теңдеулерді шешу
№1 х 4 +2х 3 -4х 2 -5х-6=0 теңдеуінің түбірлері жататын интервалды анықтау және түбірің табыңыз.
Шешуі: Берілген теңдеуде а 1 =2, а 2 =-4, а 3 =-5, а 4 =-6.
p
=
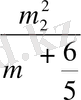 ,
q
=
-
,
q
=
-
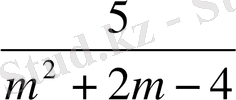 .
.
p мен q үшін
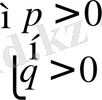
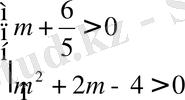
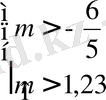
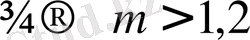


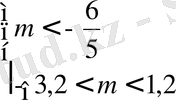
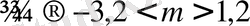
Берілген теңдеу түбірі -3, 2 < m < -1, 2 және m>1, 2 аралықтарында жатады.
Енді теңдеу түбірін табайық. Ол үшін анықталған аралықтардағы p мен q- дың мәндерін есептейміз.
Егер m = -2 болса
p=
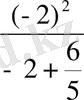 =-5
,
q
=
=-5
,
q
=
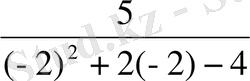 =-1, 25
=-1, 25
Егер m = -2 болса
p=
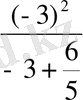 =-5
,
q
=
=-5
,
q
=
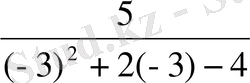 =-5
=-5
Демек, m = -2 теңдеудің түбірі
Енді m >1, 2 аралығын қарастырайық. Егер m = 2 болса
p=
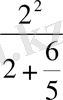 =1, 25
,
q
=
=1, 25
,
q
=
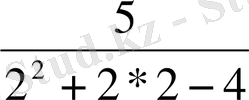 =1, 25
=1, 25
Демек, m = 2 теңдеудің екінші түбірі
Егер m = 3 болса, онда
p=
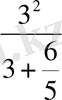 =
=
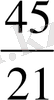 ,
q
=
-
,
q
=
-
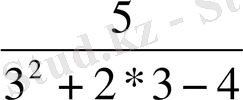 =
=
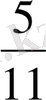
Егер m =4 болса, онда
p=
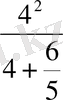 =
=
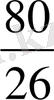 ,
q
=
-
,
q
=
-
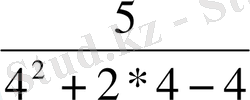 =
=
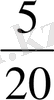
Егер m =5 болса, онда
p=
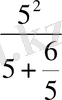 =
=
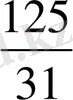 ,
q
=
-
,
q
=
-
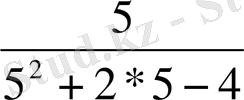 =
=

Тағы сол сияқты жалғастыра беруге болады. Бірақта
m
үлкейген сайын
p=
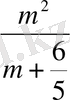 , үлкеюде, ал
q
=
-
, үлкеюде, ал
q
=
-
 азаюда. Сондықтан
m ≥2
жағдайында теңдеудің түбірі болмайды. Себебі, жоғары есептеулерден көрінгендей, олар бір-біріне тең болу мүмкіндігі жоқ.
азаюда. Сондықтан
m ≥2
жағдайында теңдеудің түбірі болмайды. Себебі, жоғары есептеулерден көрінгендей, олар бір-біріне тең болу мүмкіндігі жоқ.
Сонымен х 4 +2х 3 -4х 2 -5х-6=0 теңдеуінің 2 нақты түбірі бар. Олар х 1 =-3, x 2 =2 қалған түбірлері комплекс сандар. Мұндай қорытындының дұрыстығына төмендегіше көз жеткізуге болады. х 4 +2х 3 -4х 2 -5х-6 көпмүшелігін төмендегіше көбейткіштерге діктеуге болады:
х 4 +2х 3 -4х 2 -5х-6=(х+3) (х-2) (х 2 +х+1) =0
Бұл теңдеуден х=-3, х=2 түбіртегі екендігі көрініп тұр.
Ал
х
2
+х+=0
теңдеуіш түбірледі
х
3, 4
=(-1
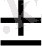 і
і
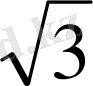 х) /2
х) /2
№2 х3+7х 2 -18х-1444=0 теңдеуінің шешімін табыңыз.
Шешуі: p, q, p 1 , q 1 - ларды есептейік:
p=
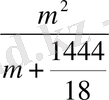 ,
q
=
-
,
q
=
-
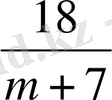 , p
1
=
, p
1
=
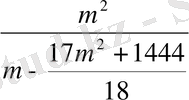 ,
q
1
=
-
,
q
1
=
-
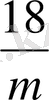
х 3 +7х 2 -18х+1444=0 теңдеуінің түбірлері орналасқан интервалдын анықтайық. Ол үшін (14) -(17) пайдаланасыз.
1)
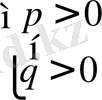
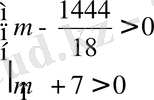
 m>
m>
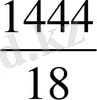
2)

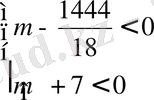
 m<-7
m<-7
Демек, теңдеу түбірлері
m < -7, m>
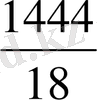 аралықтарында жатады.
аралықтарында жатады.
3)
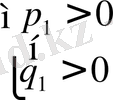
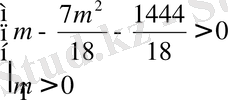 Бұл системаның шешімі жоқ
Бұл системаның шешімі жоқ
4)
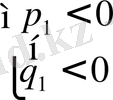
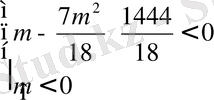
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz