Аксонометриялық проекциялар: теориясы, түрлері және бұрмалану көрсеткіштері


Аксонометриялық проекциялар туралы жалпы мағлұмат
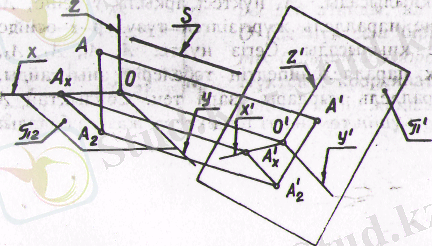
Нәрсенің аксонометриялық проекциясын (қысқаша аксонометриясын) тұрғызу үшін оны қозғалмайтын тік бұрышты координаттар жүйесімен байланыстырады. Одан кейін нәрсені, координаттар жүйесімен бірге жазықтыққа проек-циялайды.
Мысалы, беріл-ген
А
нүктесінің аксонометриясын салуды қарастырайық (1-сурет) . Нүктенің
Oxyz
координаттар жүйесіндегі координаттарын анықтайық.
А
нүктесінен
 жазықтығына түсірілген перпендикуляр оны
жазықтығына түсірілген перпендикуляр оны
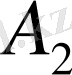 нүктесінде қияды.
нүктесінде қияды.
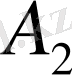 нүктесі арқылы
у
өсіне параллель жүргізілген түзу
х
осін
А
х
нүктесінде қияды.
нүктесі арқылы
у
өсіне параллель жүргізілген түзу
х
осін
А
х
нүктесінде қияды.
- сурет)
Сонда
берілген нүктенің абсциссасын,
- ординатасын және
- аппликатасын анықтайды.
сынық сызығын А нүктесінің натурал координаттық сынық сызығы дейді, ал Oxyz жүйесін натурал координаттар жүйесі дейді.
Қалауымызша орналасқан проекция жазықтығын және проекциялау бағытын 5 тағайындаймыз. Берілген нүктені натурал жүйемен бірге
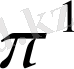 жазықтығына s бағытында проекциялаймыз. Сонда натурал
Oxyz
жүйе аксонометриялық координаттар жүйесі деп аталатын
жазықтығына s бағытында проекциялаймыз. Сонда натурал
Oxyz
жүйе аксонометриялық координаттар жүйесі деп аталатын
 жүйесіне проекцияланады.
жүйесіне проекцияланады.
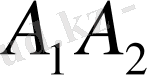 және
және
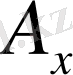 нүктелері
нүктелері
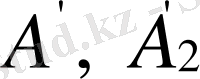 және
А'
х
нүктелеріне проекцияланады. Параллель проекцияның 3-қасиетіне байланысты
А'
х
нүктесі
х'
түзуінде жатады. Параллельдік сақталатындықтан,
және
А'
х
нүктелеріне проекцияланады. Параллель проекцияның 3-қасиетіне байланысты
А'
х
нүктесі
х'
түзуінде жатады. Параллельдік сақталатындықтан,
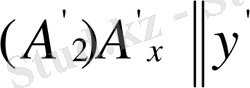 және
және
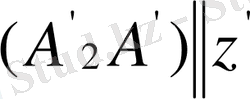 болады.
А'
берілген
А
нүктесінің аксонометриялық проекциясы (қысқаша аксонометриясы),
болады.
А'
берілген
А
нүктесінің аксонометриялық проекциясы (қысқаша аксонометриясы),
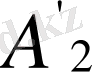 -екінші проекциясы. Керек болған жағдайда екінші проекция үшін
-екінші проекциясы. Керек болған жағдайда екінші проекция үшін
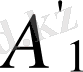 немесе
немесе
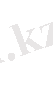
 нүктесін де алуға болады. Абсцисса өсіне параллель кесіндінің проекциясына қатынасының кері шамасын
х осі бойынша бұрмалану көрсеткіші,
ордината өсіне параллель кесіндінің проекциясына қатынасының кері шамасын
у осі бойынша бұрмалану көрсеткіші
және аппликата осіне параллель кесіндінің проекциясына қатынасының кері шамасын
z осі бойынша бұрмалану көрсеткіші
деп атайды. Бұрмалану көрсеткіштерін
и,
v
және
нүктесін де алуға болады. Абсцисса өсіне параллель кесіндінің проекциясына қатынасының кері шамасын
х осі бойынша бұрмалану көрсеткіші,
ордината өсіне параллель кесіндінің проекциясына қатынасының кері шамасын
у осі бойынша бұрмалану көрсеткіші
және аппликата осіне параллель кесіндінің проекциясына қатынасының кері шамасын
z осі бойынша бұрмалану көрсеткіші
деп атайды. Бұрмалану көрсеткіштерін
и,
v
және
 әріптеремен белгілеп, мына қатынастарды аламыз:
әріптеремен белгілеп, мына қатынастарды аламыз:
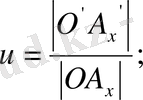
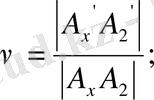
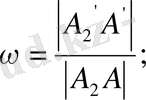
АВ кесіндісінің аксинометриясын оның үщштарының координаттары
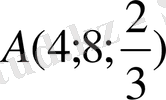 және (В (0; 4; 2) ) бойынша салуды қарастырайық. Аксонометриялық осьтерді қалауымызша 2 - суреттегідей жүргізейік. Бұрмалагну көрсеткіштер
және (В (0; 4; 2) ) бойынша салуды қарастырайық. Аксонометриялық осьтерді қалауымызша 2 - суреттегідей жүргізейік. Бұрмалагну көрсеткіштер
 ,
,
 және
және
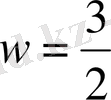 болсын. А нүктесінің абсциссасы 4-ке тең, оны бұрмалану көрсеткішіне көбейтеміз. Сонда
болсын. А нүктесінің абсциссасы 4-ке тең, оны бұрмалану көрсеткішіне көбейтеміз. Сонда
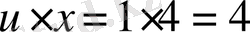 болғандықтан,
О'
нүктесінен бастап езара тең 4 кесінді салып,
болғандықтан,
О'
нүктесінен бастап езара тең 4 кесінді салып,
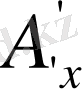 нүктесін аламыз.
нүктесін аламыз.
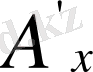 нүктесі арқылы
у
осіне параллсль түзу жүргізіп, оған
нүктесі арқылы
у
осіне параллсль түзу жүргізіп, оған
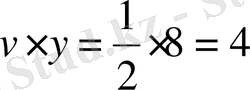 кесінді саламыз. Сонда
кесінді саламыз. Сонда
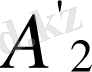 нүктесі алынады.
нүктесі алынады.
 нүктесі арқылы
нүктесі арқылы
 осіне параллель түзу жүргізіп, оның бойынша
осіне параллель түзу жүргізіп, оның бойынша
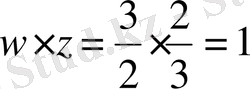 кесінді салып,
кесінді салып,
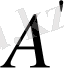 нүктесін аламыз.
В
нүктесінің абсциссасы нөлге тең. Сондықтан
О'
нүктесінен бастап
у'
осіне
нүктесін аламыз.
В
нүктесінің абсциссасы нөлге тең. Сондықтан
О'
нүктесінен бастап
у'
осіне
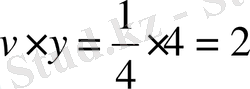 кесінді салып,
кесінді салып,
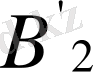 нүктесін аламыз.
В'
г
нүктесі арқылы
нүктесін аламыз.
В'
г
нүктесі арқылы
 осіне параллель түзу жүргізіп, оған
осіне параллель түзу жүргізіп, оған
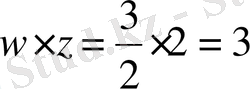 кесінді салып,
В'
нүктесін аламыз.
А'
және
В'
нүктелерін түзу кесіндімен қосу керек. Сонда алынған
А'В'
кесіндісі
АВ
кесіндісінің аксонометриясын береді.
кесінді салып,
В'
нүктесін аламыз.
А'
және
В'
нүктелерін түзу кесіндімен қосу керек. Сонда алынған
А'В'
кесіндісі
АВ
кесіндісінің аксонометриясын береді.
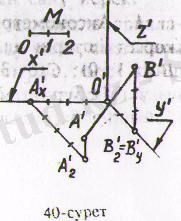
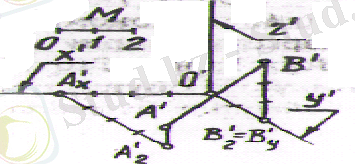
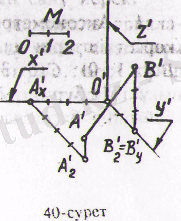
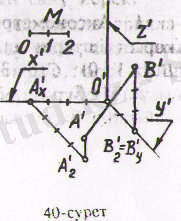
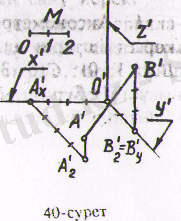
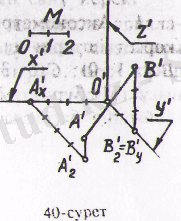
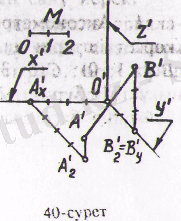
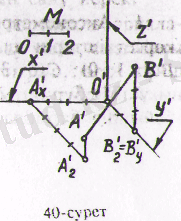
(2-сурет)
Проекциялау бағыты проекция жазықтыгана перпендикуляр болса, аксонометрия тік бұрышты деп аталады. Тік бұрышты аксонометрия үшін
. Егер проекциялау бағыты проекция жазықтығына псрпендикуляр болмаса, аксономстрия қиғаш бұрышты деп аталады. Жалпы жағдайда
болуы мүмкін. Аксонометрияның
болатын жеке түрін изометрия дейді ( «изометрия» грек сөзі, казақшаға аударғанда «бірдей өлшем» деген мағына береді), ал бұрмалану көрсеткіштерінін екеуі өзара тең және олар үшіншісіне тең болмайтын түрін диметрия деп атайды («диметрия» грек сөзі, «екі өлшем» дегенді білдіреді) .
Аксонометриялық проекциялар жағзықтығының натурал жүйеге
қарағандағы орналасуына және проекциялау бағытына байланысты аксонометриялық осьтердің
 және
және
 ) арасындағы бұрыш әр түрлі болуы мүмкін, оларға ешқандай шек қойылмайды. Тік бұрышты аксонометрия үшін
) арасындағы бұрыш әр түрлі болуы мүмкін, оларға ешқандай шек қойылмайды. Тік бұрышты аксонометрия үшін
 болады. Сондықтан бұрмалану көрсеткіштерінің екеуін қалауымызша тағайындауға болады. Осы айтылғандардан аксонометрияның өте көп екенін аңғарамыз. Біз олардың екеуімен ғана танысамыз. Олар -
тік бұрышты изометрия мен қиғаш бұрышты фронталь диметрия.
болады. Сондықтан бұрмалану көрсеткіштерінің екеуін қалауымызша тағайындауға болады. Осы айтылғандардан аксонометрияның өте көп екенін аңғарамыз. Біз олардың екеуімен ғана танысамыз. Олар -
тік бұрышты изометрия мен қиғаш бұрышты фронталь диметрия.
Аксонометриялық проекциялар туралы
түсінік және олардың түрлері
Техникалык сызбаларды орындағанда кейбір жағдайда ортогональ проекцияларымен қоса көркекі кескіндерді де қолдану қажет болады. Көрнекі кесіндерді салудың бірі аксонометриялық -проекциялар (аксонометрия) -пайдаланылады. Аксонометрия, осьтер бойымен өлшеу деген мағына беретін грек сөздерінен шығады (аксон - ось, метрео - өлшеу) .
Аксонометриялық проекциясын алу үшін фигураны кеңістіктегі тік бұрышты координаттар жүйесіне бекітеді. Кеңістіктегі координаттар жүйесі - өзара перпендикуляр абсцисса х, ордината у, аппликата z осьтерінен және осы осьтермен анықталатын xoz, xoy, yoz координат жазықтықтарынан құралады. Содан соң параллель проекциялаушы сәулелер арқылы аксонометриялык про-екция жазықтығына (а) проекциялайды (3-сурет) .
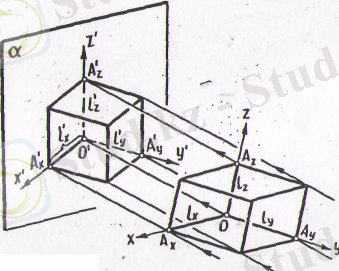
(3 - сурет)
Нәрсе бекітілген координаттар осьтерінің проекциялары аксонометриялық осьтер деп аталады. Қеңістіктегі координат осьтерінің (х, у, z) бойларынан ұзындығы l -ге тең кесінділер алайық. Олардың аксонометриялық проекциялары, яғни
кесінділері аксонометриялық осьтер бойындағы өлшем бірліктері болады немесе асконометриялық бірлік (аксонометриялық масштаб) деп аталады.
Аксонометрияда нәрсенің сызықтық, бұрыштық өлшемдері жалпы жағдайда өзгеріп түседі. Кесінді проекциясы ұзындығының сол кесіндінің нақты ұзындығынақатынасы өзгеру көрсеткіші (коэффициенті) деп аталады:
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz