Туындының физикалық және геометриялық мағынасы. Функцияның графигіне жүргізілген жанама

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 4 бет
Таңдаулыға:

ТУЫНДЫНЫҢ ФИЗИКАЛЫҚ ЖӘНЕ ГЕОМЕТРИЯЛЫҚ МАҒЫНАСЫ. ФУНКЦИЯНЫҢ ГРАФИГІНЕ ЖҮРГІЗІЛГЕН ЖАНАМА

Функция, функцияның және аргументтің өсімшесі, туындының анықтамасы, жанама.

Осы тақырыпты оқу барысында сендер нені үйреңесіңдер?

Бұл тақырыпты игере отырып, туындының физикалық және оларды есеп шығаруда қолдануды үйренесіңдер.

Алдымен туындының физикалық мағынасын қарастырайық.

Түзу сызық бойымен қозғалған физикалық деңенің 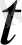уақыт ішінде жүріп өткен жолы 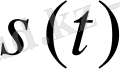функциясымен берілсін. Қозғалыстағы дененің 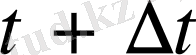уақыт өткеннен кейінгі жолы функциясымен анықталады. Сонда уақыт 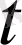-дан 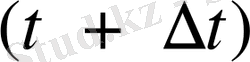дейін өзгергенде, жолдың шамасы

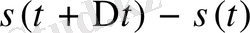
айырымымен анықталады. Енді осы айырымды уақытқа бөлсек,

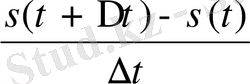
яғни қозғалыстағы дененің орташа жылдамдығы

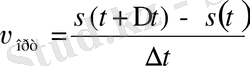
шығады.

Соңғы өрнектен нөлге ұмтылғандағы шекке көшсек,

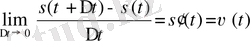
теңдігін аламыз. Мұндағы 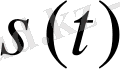- қозғалыстағы дененің 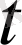уақыт ішіндегі жүрген жолы, ал 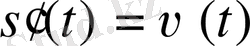- қозғалыстағы дененің 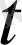уақыт мезетіңдегі лездік жылдамдығы.

Биіктіктен еркін құлаған дененің 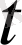уақыт ішіндегі жүрген жолы 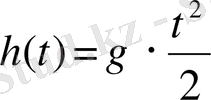функциясымен анықталатыны физика курсынан белгілі. 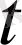уақыт мезетіндегі дененің құлау жылдамдығы 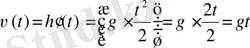, яғни 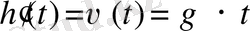, мұндағы 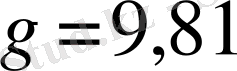м/с ² - еркін құлаған дененің үдеуі.

Демек, 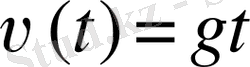өрнегі берілген 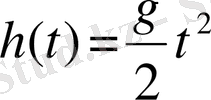теңдеуіне сәйкес қозғалатын дененің (функцияның) лездік жылдамдығын береді.

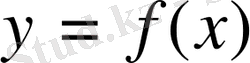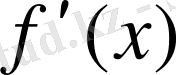Жалпы, функциясының х нүктесіндегі туындысы оның х нүктесіндегі өзгеру жылдамдығын анықтайды. Бұл туындының физикалық мағынасы.

Егер 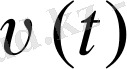жылдамдықтан туынды табатын болсақ, онда 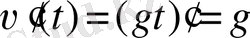шығады. Ал жоғарыдағы айтылған бойынша, - үдеу. Демек, жылдамдықтан алынған туынды үдеуге тең.

1-мысал. Қозғалыстағы дененің жүрген жолв 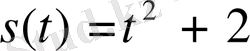формуласымен берілген. Осы дененің с мезетіндегі лездік жылдамдығы мен үдеуін табайық.

Шешуі. Лездік жылдамдық 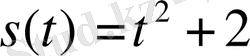функциясының туындысы бойынша анықталады.

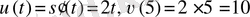. Үдеуді есептеу үшін лездік жылдамдықтан туынды алу керек, сонда

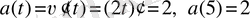
Жауабы: 10 м/с; 2 м/с ² .

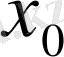функциясының нүктесінде 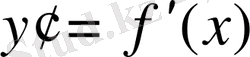туындысы бар деп ұйғарып, оның геометриялық мағынасын анықтайық.

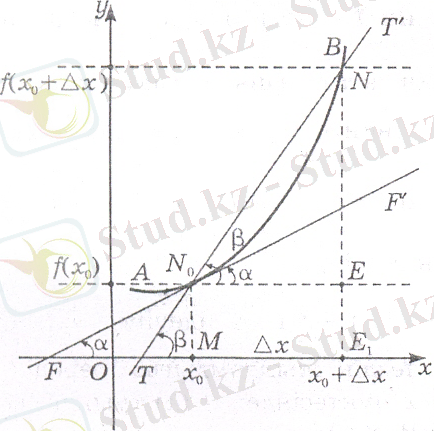
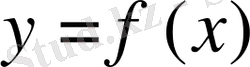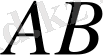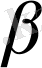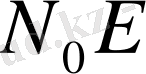51-суреттегі қисығы функциясының графигі болсын. және нүктелері қисығының бойында жатқан нүктелер. Осы екі нүкте арқылы жүргізілген қиюшы түзуі. щсінің оң бағытымен түзуінің арасындағы бұрышты деп белгілейік. осіне параллель түзуін жүргізейік. Онда 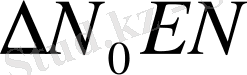- тікбұрышты үшбұрыш шығады. , , 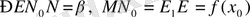себебі 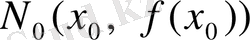және .

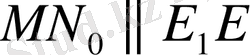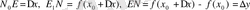
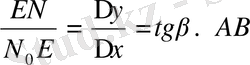қисықтың бойындағы жылжымайтын нүкте болсын, ал нүктесін қисықтың бойымен жылжытып, нүктесімен беттессін деп ұйғарайық.

Сонда өтюшы қисықтын нүктесіндегі жанамасы, яғни түзуіне айналады. Қиюшы мен осінің оң бағытының арасындағы 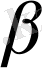бұрышы жанама мен осінің оң бағытының арасындағы бұрышына айналады

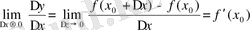
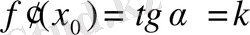(1) (1) формула туындының геометриялық мағынасын береді.

Сонымен, туындының геометриялық мағынасы функцияның графигіне жүргізілген жанаманың бұрыштық коэффициенті.

2-мысал. 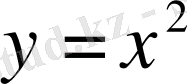параболасына 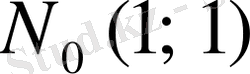нүктесінде жүргізілген жанама мен осінің оң бағытының арасындағы бұрышын табайық.

Шешуі. 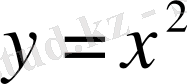функциясының туындысы 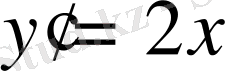. (1) формула бойынша 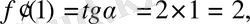ал жанама мен щсінің оң бағытының арасындағы бұрыша .

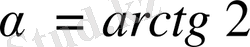Жауабы: arctg 2.

Кез келген қисықтың 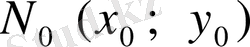нүктесінде жүргізілген жанамасының теңдеуін қорытып шығарайық.

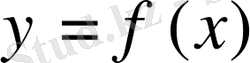функциясы және оның 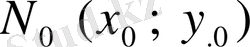нүктесіндегі 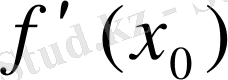туындысы берілсін.

Жанама түзу болғандықтан, жанаманың теңдеуін 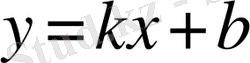сызықтық функция ретінде іздейміз. Мұндағы 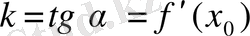, онда 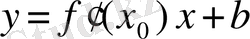болады. Осы теңдеуге 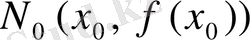нүктесінің координаталарын қоямыз. Сонда 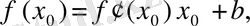осыдан

Соңғы теңдеуді 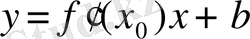теңдеуіне апарып қойсақ, 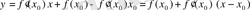. Демек,

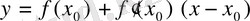(2)

Сонда (2) теңдеу жанаманың теңдеуі болып табылады.

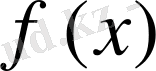функциясының графигіне 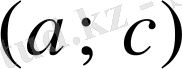интервалынан алынған абсциссасы 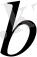-ға тең 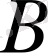нүктесінде жүргізілген 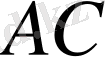жанамасы оның 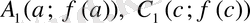нүктелері арқылы өтетінін қиюшысына параллель деген пікірдің дұрыс көрнекті түрде көрсету үшін туындының геометриялық мағынасын пайдаланайық.

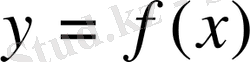
Егер функциясы дифференциалданатын болса, онда аралығында

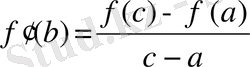(3)

болатындай нүктесі табылады.

(2) формула Лагранж формуласы деп аталады.

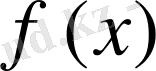функциясының графигіне абсциссасы 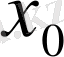болатын нүктеде жүргізілген жанаманың теңдеуін жазудың алгоритмін берейік:

1) 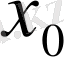-ге сәйкес 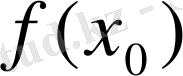-ді есептеу;

2) 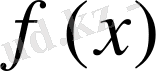функциясының туындысын табу;

3) 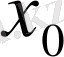-дегі туындының мәнін 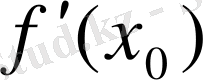анықтау;

4) табылған мәндерді (2) формулаға қойып, жанаманың теңдеуін алу.

3-мысал. 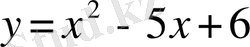функциясының абсциссалары 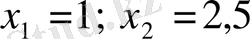және 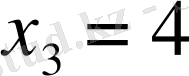болатын нүктелер арқылы өтетін жанамаларының теңдеулерін жазайық. осімен жанамаларының арасындағы бұрыштарды анықтайық.

Шешуі. Абсциссасы 1-ге тең болатын нүкте арқылы өтетін функцияның жанамасының теңдеуін жазайық.

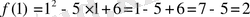. Сонымен, 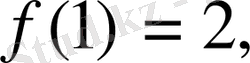жанама 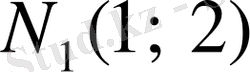нүктесінен өтеді.

Функцияның туындысын табайық 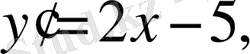сонда .

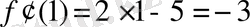Енді (2) формуланы пайдаланып, 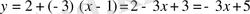аламыз.

Сонымен, 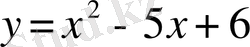параболаның 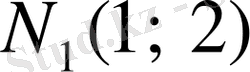нүктесі арқылы өтетін жанамасының теңдеуі .

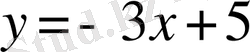Тура осылай абсциссалары 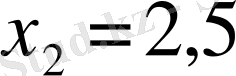және 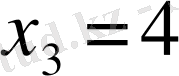нүктелері арқылы өтетін жанамаларның теңдеулерін анықтасақ, сәйкесінше 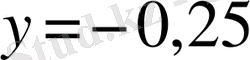және 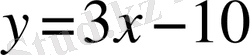болады.

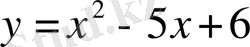
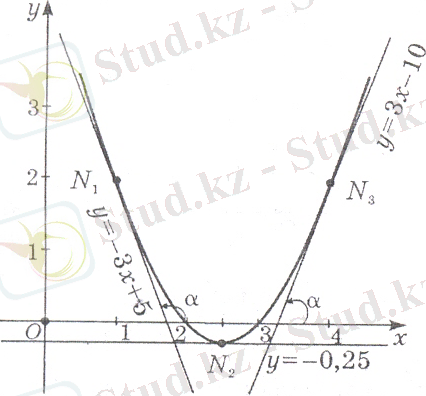
бұрышы 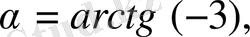себебі

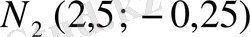нүктесінен өтетін жанаманың осіне жасайтын бұрышы , себебі 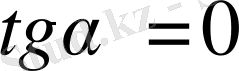(жанама осіне параллель) .

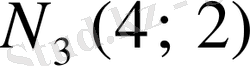нүктесінен өтетін жанама мен осінің оң бағытымен жасаған бұрышы 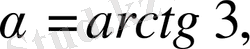себебі .

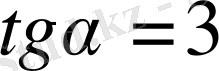Сонымен, қарастырылған мысалдан келесі қорытындыны жасауға болады. Функцияның графигіне берілген нүктеде жүргізілген жанама мен осінің оң бағытының арасындағы бұрыш: