Зарядталған бөлшектердің электромагниттік өрісте қозғалысы

Пән: Физика
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 19 бет
Таңдаулыға:

Мазмұны

Кіріспе . . . 3

І. Негізгі бөлім

1. 1 Зарядталған бөлшектердің электромагниттік өрісте қозғалысы . . . 4

1. 2 Қозғалыстағы зарядталған бөлшектердің электр және магнит өрістері

әсерімен бұрылуы . . . 6

1. 3 Зарядталған бөлшектердің үдеткіштері. Циклотрон . . . 9

1. 4 Резонанстық және резонанстық емес үдеткіштер . . . 10

Қорытынды . . . 18

Пайдаланылған әдебиеттер . . . 19

Кіріспе

Үдеткіштер - электр және магнит өрісінің көмегімен жоғары энергиялы зарядталған бөлшектер (электрондар, протондар, ядролар мен иондар) ағындарын түзетуге арналған қондырғылар. Үдеткіштердің басты көрсеткіштері: бөлшектердің энергиясы мен шоқтың қарқыны, яғни бірлік уақыт ішінде ұшып шығатын бөлшектер саны. Шоқтың қарқының ол түзетін токтың күшімен жиі сипаттайды. Тоқ күші, әрине, уақыт бірлігінде ұшып шығатын бөлшектердің саны мен олардың зарядының көбейтіндісіне тең.

Үдетілген бөлшектер ағынын түзетудің ең қарапайым әдісі-олардың электр өрісін өткізу. Электр өрісінде потенциалдар айырмасы V, бір-бірінен d қашықтықта орналасқан екі электродтан тұрады. Әйтпесе, бөлшектердің ауаның молекулаларымен соқтығысуынан оларды үдету мүмкін емес болады. Үдетілген бөлшектердің электр өрісіне кіруі мен шығуын қамтамасыз ету үшін электродтар тор немесе сақина түрінде жасалады. Ыдыстағы вакуумды сорғыш қамтамасыз етеді.

Үдететін электр өрісінің сипатына қарай, үдеткіштер резонанстық емес және резонанстық болып жіктеледі.

Резонанстық емес үдеткіштерде электр өрісінің бағыты үдету кезінде өзгермейді. Резонанстық үдеткіштерде айнымалы электр өрісі қолданылып, бөлшектер қозғалысы өрістің өзгеруімен резонанста болып, онымен бірге қозғалады.

1. 1 Зарядталған бөлшектердің электромагниттік өрісте қозғалысы

Біртекті магнит өрісіне В векторына перпендикуляр болатын v жылдамдықпен е' заряды ұшып келді делік. Лоренц күшінің әсерімен заряд шамасы жағынан тұрақты болып келген қалыпты үдеуге ие болады:

w _n = $\frac{f}{m}$ = $\frac{е'}{m\ }$ v B (1. 1)

( v мен В арасындағы бұрыш тік болады) .

Егер жылдамдық тек бағыты бойынша өзгеретін болса, шамасы жағынан тұрақты болып келетін қалыпты үдеумен қозғалған қозғалыс радиуысы w _n = v ² /R шартымен анықталатын шеңбер бойындағы бір қалыпты қозғалыс болады. Бұған w _n - ға (1) мәнін қойып, ал осыдан шыққан теңдеуді R- ге қатысты шығарып, мынаны табамыз:

R= $\frac{m}{е'}$ $\frac{v}{B}$ (1. 2)

Сонымен, v векторы В векторына перпендикуляр болған жағдайда зарядталған бөлшек радиусы бөлшектің жылдамдығына, өрістің магнит индукциясына және е' бөлшегі зарядының оның m массасына қатынасына тәуелді (шеңбер бойымен қозғалады) . е'/m қатынасы меншікті заряд деп аталады.

Бөлшектің бір айналымына кететін Т уақытын табайық. Бұл үшін шеңбердің 2 $\pi$ R ұзындығын бөлшектің v жылдамдығына бөлеміз. Осының нәтижесінде мынаны шығарып аламыз:

Т=2 $\pi$ $\frac{m}{е'}$ $\frac{1}{В}$ (1. 3)

Бөлшектің шеңбер бойымен айналу периоды оның жылдамдығына тәуелді болмайды екен, ол период тек бөлшектің меншікті заряды мен өрістің магнит индукциясы бойынша ғана анықталады. 1-суретте меншікті зарядтары бірдей, бірақ v ₁ және v ₂ жылдамдықтары әр түрлі болатын екі бөлшектің біртекті магнит өрісінде қозғалатын траекториясы көрсетілген. Егер бөлшектер бір мезгілде О нүктесінен шықса, онда олар бірдей уақыт ішінде толық айналым жасап, тағы да О нүктесінде кездеседі.

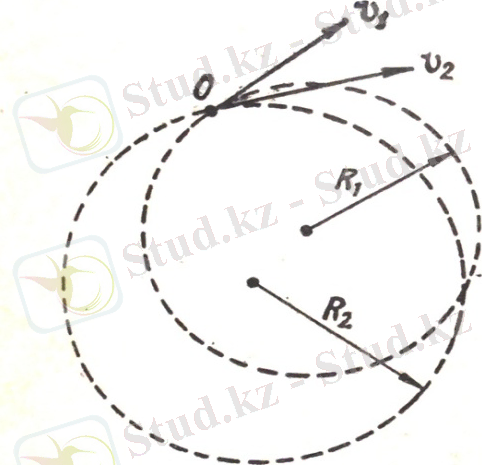$C:\Users\нургелды\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\20140404_222302.jpg$ 1-сурет

Зарядталған бөлшектің жылдамдығы біртекті магнит өрісінің бағытымен, $\pi$ / 2 -ден өзгеше, $\alpha$ бұрышын жасаған жағдайындағы осы бөлшектің қозғалу сипатын анықтайық. v векторын $v_{⟘} -$ В векторына перпендикуляр және v‖ - В векторына параллель екі құраушыға жіктейік (2- сурет) :

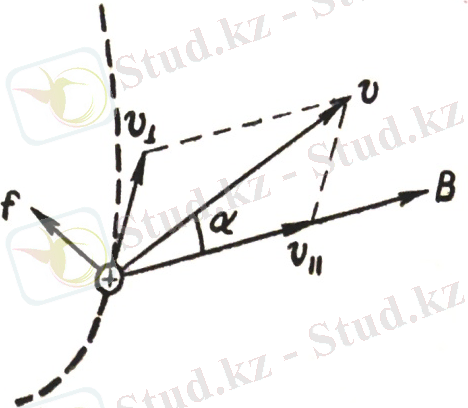$C:\Users\нургелды\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\20140404_222549.jpg$ 2-сурет

$v_{⟘}$ = vsin $\ \alpha$ , $v_{\}$ = vcos $\ \alpha$

екендігін көру қиын емес.

Лоренц күші мынаған тең:

f = е' vB sin $\ \alpha$ = е' $v_{⟘}$ B

және ол В векторына перпендикуляр жазықтықта жатады. Осындай күшпен туатын үдеу ${\ v}_{⟘}$ үшін қалыпты үдеу болады. Лоренц күшінің В векторы бағытындағы құраушысы нольге тең; сондықтан бұл күш $v_{\}$ шамасына әсер ете алмайды. Сөйтіп, бөлшектің қозғалысын екі қозғалыстың : 1) В векторы бағытының бойымен тұрақты $v_{\}$ = vcos $\ \alpha$ жылдамдығымен орын ауыстырудың және 2) В векторына перпендикуляр жазықтықта бір қалыпты айналудың қабаттасуы деп есептеуге болады. Бойымен айналыс өткен шеңбердің радиусы (2) формуласымен анықталады, мұнда v- нің орнына $v_{⟘}$ = vsin $\ \alpha$ алынады. Қозғалыс траекториясы осі В векторы бағытымен дәл келетін (3-сурет) спираль болады.

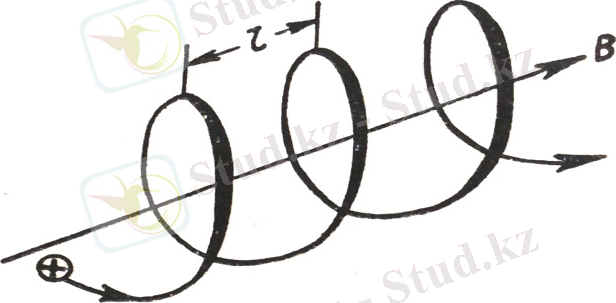$C:\Users\нургелды\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\20140404_222337.jpg$ 3-сурет

Спиральдың l алымын $v_{\}$ - ны айналу Т периоды анықталатын (1. 3) формуласына көбейтіп табуға болады:

l = $v_{\}$ T= 2 $\pi$ $\frac{m}{е'}$ $\frac{1}{В}$ vcos $\ \alpha$ . (1. 4)

Спираль бұрылатын бағыт бөлшек зарядының таңбасына тәуелді болады. Егер заряд оң болса, онда спираль сағат тіліне қарсы бұрылады. Бойымен теріс зарядталған бөлшек қозғалатын спираль сағат тілінің бағытымен бұралады (біз спиральға В векторының бағытымен қарап тұрмыз деп ұйғарылады, сонда бөлшек егер $\propto < \pi$ /2 болса, бізден әрі қарай және егер $\ \propto > \pi$ /2 болса, бізге қарай зымырайды) .

1. 2 Қозғалыстағы зарядталған бөлшектердің электр және магнит өрістері әсерімен бұрылуы

Бірдей зарядталған бөлшектердің (мысалы, электрондардың) жіңішке шоғын қарастырайық, бұл шоқ өзіне перпендикуляр болатын экрандағы О нүктесіне түседі (4-сурет) .

$C:\Users\нургелды\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\20140404_222354.jpg$ 4-сурет

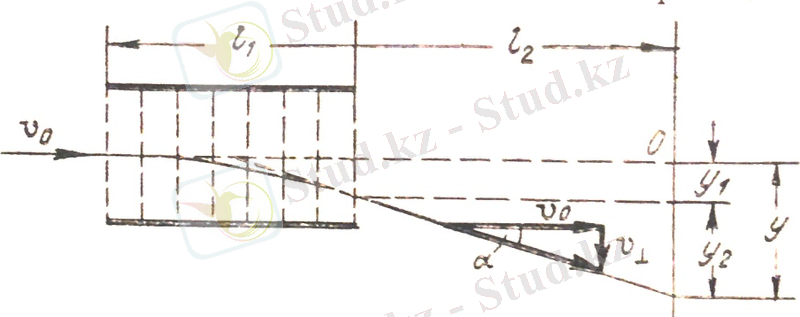
Бөлшек шоғына перпендикуляр болатын біртекті электр өрісінің ұзындығы l ₁ жолда әсер етуінен туатын осы бөлшек ізінің ығысуын анықтайық. Бөлшектің бастапқы жылдамдығы υ ₀ -ге тең болсын. Өріс аймағына енісімен әрбір бөлшек шамасы мен υ ₀ векторына перпендикуляр бағыты жағынан тұрақты $\mathbf{w}_{\mathbf{⟘}} = \frac{e'}{m}\mathbf{E}$ ( $\frac{e'}{m}\$ - бөлшектің меншікті заряды) үдеумен қозғалады. Қозғалыс өріс әсерінен t=l ₁ /υ ₀ уақытқа созылады. Осы уақыт ішінде бөлшек мынадай:

${\ y}_{1} = \frac{1}{2}\omega_{⏊}t^{2} = \frac{1}{2}\frac{e'}{m}\mathbf{E}\frac{l_{1}^{2}}{\upsilon_{\mathbf{0}}^{\mathbf{2}}}$ (2. 1)

қашықтыққа ығысады да, υ ₀ векторына перпендикуляр болатын құраушы жылдамдыққа ие болады:

$\upsilon_{⏊} = \omega_{⏊}t = \frac{e'}{m}\mathbf{E}\frac{l_{1}}{\upsilon_{0}}$

Бұдан былай бөлшек υ ₀ векторымен α бұрышын жасайтын бағытта түзу сызық бойымен ұшады, ал α бұрышы мына шарттан анықталады:

$tg\alpha = \frac{\upsilon_{⏊}}{\upsilon_{0}} = \frac{e'}{m}\mathbf{E}\frac{l_{1}}{\upsilon_{0}^{2}}.$ (2. 2)

Осының нәтижесінде бөлшек шоғы (1) ығысуына қосымша мынадай ығысуға ие болады:

$y_{2} = l_{2}tg\alpha = \frac{e'}{m}\mathbf{E}\frac{l_{1}l_{2}}{\upsilon_{0}^{2}}$ ,

мұндағы l ₂ - өрістің шекарасында экранға дейінгі қашықтық.

Сөйтіп, бөлшек шоғы ізінің О нүктесіне қатысты ығысуы мынаған тең:

$y = y_{1} + y_{2} = \frac{e'}{m}\mathbf{E}\frac{l_{1}}{\upsilon_{0}^{2}}\left( \frac{1}{2}l_{1} + l_{2} \right) .$ (2. 3)

осыдан өрісті тастап шыққан бөлшек (2. 2) формуласымен анықталатын α бұрышымен өріс жасайтын конденсатор центрінен шыққандай болып ұшады деген қорытынды шығады.

Енді ұзындығы l ₁ бөлшек жолына олардың υ ₀ жылдамдығына перпендикуляр болатын біртекті магнит өрісі қосылады деп ұйғарайық (5-сурет; өріс сурет жазықтығына перпендикуляр, ал өріс аймағы пунктир шеңберімен қоршалған) .

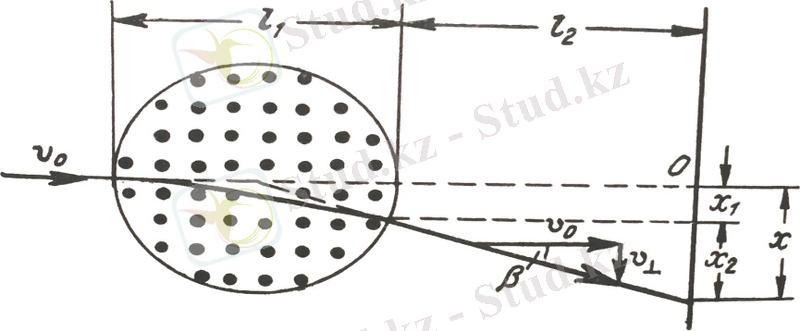
$C:\Users\нургелды\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\20140404_222417.jpg$

5-сурет

Өріс әсерінен әрбір бөлшек шамасы жағынан тұрақты $\omega_{⏊} = \frac{e'}{m}\upsilon_{0}B$ үдеуін алады. Бөлшек шоғының өріс әсерінен бұрылуы шамалы жағдаймен шектеліп, $\omega_{⏊}$ үдеуі де бағыты бойынша тұрақты және υ ₀ векторына перпендикуляр деп санауға болады. Сонда бөлшектің ығысуын есептеп шығару үшін біздің бұрын тапқан формулаларымызды пайдалануға болады, бірақ олардағы $\omega_{⏊} = \frac{e'}{m}\mathbf{E}$ үдеуін $\omega_{⏊} = \frac{e'}{m}\upsilon_{0}B$ мәнімен алмастыру керек. Осының нәтижесінде бөлшектің ығысуы үшін, енді біз оны x әрпімен белгілейміз, мынаны шығарып аламыз:

$x = \frac{e'}{m}\mathbf{B}\frac{l_{1}}{\upsilon_{0}}\left( \frac{1}{2}l_{1} + l_{2} \right) .$ (2. 4)

Бөлшек шоғының магнит өрісі әсерінен бұрылатын бұрышы мына өрнекпен анықталады:

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ tg\beta = \frac{e'}{m}\mathbf{B}\frac{l_{1}}{\upsilon_{0}}.$ (2. 5)

(5) өрнекті ескере отырып, (4) формуланы мынадай етіп жазуға болады:

$x = tg\beta\left( \frac{1}{2}l_{1} + l_{2} \right) .$

Демек, бөлшектер шамалы бұрылғанда магнит өрісін тастап шығып, шамасы (2. 5) өрнегімен анықталатын β бұрышымен осы өріс центрінен шыққандай болып ұшады.

Бөлшектің электр өрісі әсерінен (2. 3) бұрылуы да, магнит өрісі әсерінен (2. 4) бұрылуы да бөлшектің меншікті зарядына және тиісті өрістің кернеулігіне (немесе индукциясына) пропорционал екендігін ескертейік. Бөлшектің екі бұрылуы да υ ₀ -ге тәуелді болады. е'/т және υ ₀ шамалары бірдей бөлшектер өрістің әрқайсысынан бірдей бұрылады, демек, олар экранның бір нүктесіне түседі.

Электрондар шоғының электр немесе магнит өрісінің әсерімен бұрылуы электон-сәулелік трубкада пайдаланылады. Электрлік бұрылу пайда болатын трубканың ішіне (6-сурет) шапшаң электрондардың жіңішке шоғын (электрондық сәуле) жасайтын электрондық пожектор деп аталатыннан басқа, өз ара перпендикуляр екі қос плпастина орналастырылады.

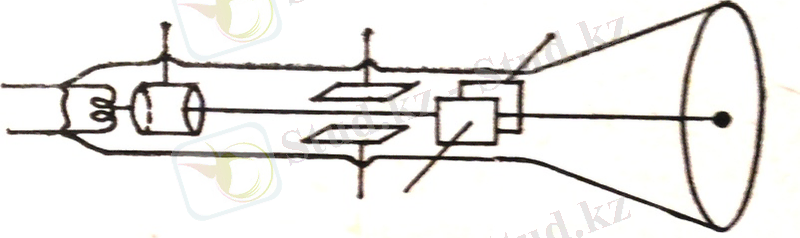
$C:\Users\нургелды\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\20140404_222442.jpg$

6-сурет

Пластинаның кез келген қосағына кернеу беріп, оған попорционал болатын (алынған пластинаға перпендикуляр бағыттағы) электрондық сәуленің ығысуын туғызуға болады. Трубканың экранын флуоресценциялаушы (сәулелендіретін) қоспамен қаптайды. Сондықтан электрондық сәуленің экранға түскен жерінде айқын жарқырайтын дақ пайда болады.

Электрон-сәулелік трубка осциллографтарда, тез өтетін процестерді бақылауға әрі суретке түсіруге мүмкіндік беретін приборларда қолданылады. Бұрылатын пластинаның бір қосағына, уақытқа байланысты сызықтық жолмен өзгеретін кернеу, ал екіншісіне зерттелетін кернеу беріледі. Электрондық сәуле инерциялығының тым аз болуынан оның бұрылу ауытқытатын пластиналар кернеуінің өзгеруі соңынан кешікпей еріп отырады, сонымен қатар электрондық сәуле осциллограф экранында зерттелетін кернеудің уақытқа тәуелділігінің графигін сызады. Көптеген электрлік емес шамалар өздеріне сәйкес келетін құрығының (датчиктің) көмегіменэлектрлік кернеуге (немесе токқа) түрленуі мүмкін. Сондықтан осциллографтар көмегімен табиғаты түрлі-түрлі болатын процестерді зерттейді.

Электрон-сәулелік трубка телевизиялық құрылғының ажырамастай бөлігі болып табылады. Телевидениеде көбінесе электрондық сәулені магнитпен басқаратын трубкалар қолданылады. Осындай трубкаларда сәулені бұрылтатын пластиналардың орнына сыртқы орналастырылған, өз ара перпендикуляр екі катушка жүйесі болады, олардың әрқайсысы электрондық сәулеге перпендикуляр болатын магнит өрісін тудырады. Катушкадағы токты өзгерте отырып, экрандағы электрондық сәуледен пайда болатын жарық дақтың орнын ауыстырамыз.

1. 3 Зарядталған бөлшектердің үдеткіштері. Циклотрон

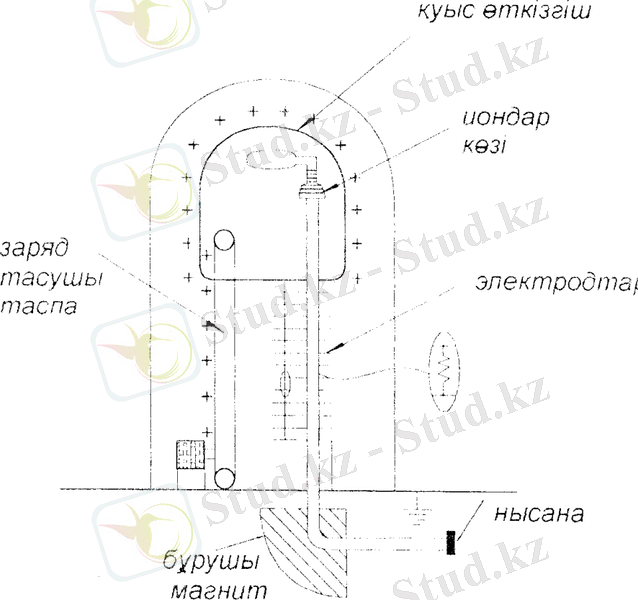
Зарядталған бөлшектердің біртекті магнит өрісінде айналу периодының оның жылдамдығына тәуелсіздігі [(1. 3) формуланы қараңыздар] циклотрон деп аталатын зарядталған бөлшектер үдеткішінің негізі болды. Бұл прибор аласа жарты дөңгелек қорап түрінде жасалған екі электродтан тұрады. (7-сурет) .

$C:\Users\нургелды\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\20140404_222516.jpg$

7-сурет

Мұндай электродтар дуанттар деген атқа ие болған. Ауасы сорып алынған корпусқа алынған дуанттар үлкен электромагнит полюстарының аралығына орналастырылады. Электромагнит туғызатын өріс біртекті, әрі дуанттар жазықтығына перпендикуляр. Дуанттарға жоғары жиілікті генератор полюстарынан алынатын айнымалы кернеу беріледі.

Кернеу ең үлкен шамасына жеткен мезетте дуанттар арасындағы саңылауға оң зарядталған бөлшек енгізейік. Сонда бөлшекті электр өрісі ілестіре отырып теріс электродтың ішіне қарай тартып әкетеді. Дуанттың ішіндегі кеңістік эквипотенциал кеңістік болады, демек, ондағы бөлшек тек магнит өрісінің әсерінде ғана болады. Бұл жағдайда зарядталған бөлшек радиусы бөлшек жылдамдығына пропорционал болатын шеңбер бойымен қозғалады [(1. 2) формуланы қараңыздар] . Дуанттар арасындағы кернеудің өзгеру жиілігін былай таңдап аламыз: бөлшек шеңбердің жартысынан өтіп, дуанттар арасындағы саңылауға келген кезде олардың арасындағы потенциалдар айырмасы таңбасын өзгертіп, амплитудалық мәніне жететіндей мезетті таңдап аламыз. Сонда бөлшек тағы да үдетіледі де, екінші дуантқа оның бірінші дуантта қозғалғандағысынан гөрі екі есе көп энергиямен ұшып кіреді. Үлкен жылдамдыққа ие болған бөлшек екінші дуантта радиусы үлкенірек (R $\sim\upsilon$ ) шеңбер бойымен қозғалатын болады, бірақ бөлшектің шеңбер жартысынан өтетін уақыты бұрынғыдай болып қалады (ол уақыт 𝜐 жылдамдығына тәуелді емес) . Сондықтан дуанттар арасындағы саңылауға бөлшек ұшып енген мезетте олардың арасындағы кернеу тағы да таңбасын өзгертеді де, ең үлкен шамасына жетеді.

Сөйтіп, егер кернеудің өзгеру жиілігін бөлшектің (1. 3) формуласымен анықталатын айналу периодына теңгерсек, онда бөлшек спиральға жақын келетін қисық бойымен қозғалады да, дуанттар арасындағы саңылау арқылы өткен сайын e´U (e´- бөлшек заряды, U-генератор өндіретін кернеу) мәніне тең қосымша энергия үлесін алады. Шамасы азғантай айнымалы кернеу көзіне ( $\sim 10^{5}$ В) сүйене отырып циклотрон көмегімен протонды 25 МэВ ретті энергияға дейін үдетуге болады. Өте жоғары энергия кезінде протон массасының жылдамдыққа тәуелділігі біліне бастайды, яғни бөлшектің айналу периоды артады [(1. 3) формуласы бойынша ол m массасына пропорционал] және бөлшектің қозғалысы мен үдеткіш өрістің өзгеруі арасындағы синхронизм бұзылады.

Синхронизмнің бұзылуынан құтылу үшін әрі бөлшек үлкен энергия алу үшін, не дуанттар қоректенетін кернеу жиілігін не магнит өрісінің индукциясын өзгертетін ету керек. Бөлшектің әрбір порциясын (үлесін) үдету процесінде соған сәйкес келетін үдеткіш кернеудің жиілігін кемітетін прибор фазотрон (немесе синхроциклоирон) деп аталады. Үдеткіш кернеу жиілігі өзгермейтін, ал магнит өрісінің индукциясы m/В қатынасы тұрақты қалатындай болып өзгеретін үдеткішті синхротрон деп атайды (бұл типтегі үдеткіштер тек электрондарды үдету үшін қолданылады) .

Синхрофазотрон деп аталатын үдеткіште үдеткіш кернеудің жиілігі де және магнит өрісі де өзгереді. Үдетілетін бөлшектер синхрофазотрондарда спираль бойымен емес, радиусы тұрақты болатын дөңгелек траекториясының бойымен қозғалады. Бөлшектің жылдамдығы мен массасы артқан сайын магнит өрісінің индукциясы да, (1. 2) формуласы бойынша анықталатын радиус барлық уақытта тұрақты қалатындай болып, артады. Бұл жағдайда айналу периоды бөлшек массасының артуынан да, сондай-ақ В-нің көбею салдарынан да өзгереді. Үдетуші кернеу бөлшек қозғалысымен синхронды болу үшін осы кернеудің жиілігі өзіне сәйкес келетін заң бойынша өзгеріп отыру керек. Синхрофазотронда дуанттар болмайды, сондықтан бөлшек траекторияның жеке учаскелерінде, жиілігі өзгеріп отыратын кернеу генераторынан туатын, электр өрісінің көмегімен үдетіледі.

Қазіргі уақыттағы (1969 ж) ең қуатты элементар бөлшектердің үдеткіші - протондық синхротрон - СССР-де Жоғары знергия физикасы институтында (Москва түбіндегі Серпухов қаласында) 1967 жылы іске қосылды. Ол протонды 76 ГэВ (76∙ $10^{9}$ эВ) энергияға дейін үдетеді. Осындай энергияға ие болған протон жылдамдығының бостықтағы жарық жылдамдығынан 0, 01 % -тен (𝜐=0, 2 с) кемірек айырмашылығы болады.

1. 4 Резонанстық және резонанстық емес үдеткіштер

Резонанстық емес үдеткіштердің қатарына: электростатикалық үдеткіш, жоғары энергиялы трансформаторлық үдеткіш, сатылы үдеткіш, бетатрон, сызықтық индукциялық үдеткіш кіреді.

Бұлардың алғашқы үшеуі жоғары вольттық деп аталады және өзара осы, үдететін аралыққа түсірілетін, жоғары кернеуді алу әдісімен айнытылады. Бөлшектер үдетілетін аралық бір түтік бойына орналасқан шыны немесе фарфор сақиналармен бөлінген металл шайбалардың бірталай санынан тұрады. Электродтарға кернеу резисторлардан тұратын бөлгіш арқылы беріледі. Электродтардың заты, пішіндері олар шоқтарды тиімді қалыптастыратындай етіп таңдалады.

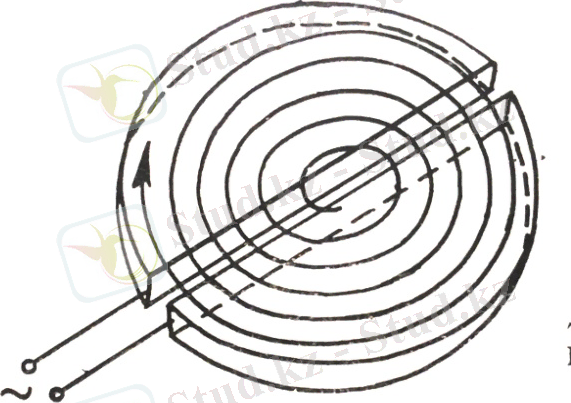
Электростатикалық үдеткіштер (Ван-де-Графф генераторы) тіке үдететін үдеткіштердің ең көп таралған түрі. Бірінші мандай үдеткішті 1931 жылы Ван-де-Графф құрастырды.

Ван-де Графф генераторы (2-сурет) электр аластатқыш бағананың басына орналасқан қуыс металл электродтан (кондуктордан), оның ішіне жоғары шеттері кіріп тұратын, тұйық электр аластатқыш лента мен үдеткіш түтіктен тұрады. Бағананың төменгі жағында лентаға зарядтағыш қондырғы заряд жапсырады. Лентамен жоғары көтерілген заряд разрядтағыш қондырғының көмегімен қырылып кондукторға беріледі. Қуыс өткізгіштің ішінде электр өрісі болмайтындықтан, заряд оның сырт бетіне жайылады. Кондуктормен үдеткіш түтіктің потенциалы ең үлкен электроды жалғанған.

Үдетілген иондар кондуктордың ішінде үдеткіш түтіктің бас жағында орнатылған иондық көзден алынады. Олар түтікте үдетілгеннен кейін, магнит өрісінің көмегімен бұрылып, нысанаға бағытталады.

Электростатикалық үдеткіштер беретін бөлшектердің энергиясының ең үлкен мәні бағана мен қоршаған газдың аластатқыштық қасиетімен анықталады. Дағдылы атмосфералық қысымда жұмыс істейтін үдеткіштер беретін бөлшектердің энергиясын бірнеше МэВ-қа дейін, ал жоғары қысымды инертті (мысалы, азот немесе көмір қышқыл газ) газ атмосферасында орналасқан үдеткіштерде 12 МэВ-қа дейін жеткізуге болады.

$G:\үдеткіштер\Сканировать20001.TIF$

8-сурет

Ең жоғарғы энергияны Ван-де-Грааф генераторының көмегімен екі есе арттыруға болады. Ол кондукторлары біріккен екі үдеткіштен тұрады. Қондырғының бір шетіне орналасқан иондық көзден үдеткіш түтіктердің біреуіне теріс зарядталған иондар енгізіледі. Олар кондукторге дейін үдетіліп, оның ішінде орналасқан қайта зарядтағышта сындырылып, оң зарядталады. Оң зарядталған иондар екінші үдеткіште үдетіліді.

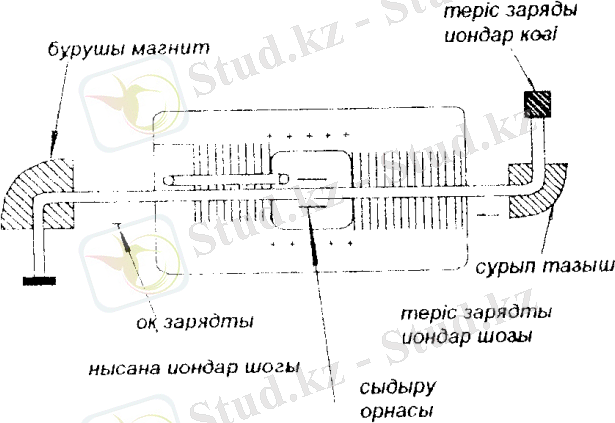
$G:\үдеткіштер\Сканировать20001 - копия.TIF$

9-сурет

Электростатикалық үдеткіштердің шектік тоғын лентаның бетінің зарядының бетінің зарядының шектік тығыздығы $\sigma$ , оның қозғалу жылдамдығы $\upsilon$ мен $l$ ені анықтайды. Оның ең үлкен қол жеткізілген мәні 500мкА. Трансформаторлық үдеткіште кернеу жоғарылатқыш трансформатордың көмегімен көтеріліп, шалаөткізгіш түзеткішпен түзетіледі. 200 кэВ-тан жоғары кернеулер алу үшін трансформатордың екінші реттік орамасын өзара аластатылған жеке бөліктерге бөліп, олардың әрқайсысының кернеуін түзетіп, тізбектей жалғайды. Бұл кезде трансформатордың магнит өзегі де өзара аластатылған бөліктерге бөлініп, әр бөлік оған сәйкес түзеткішке жалғанады.

Каскадтық үдеткіштерде кернеу, түзетілу барысында, каскадтық көбейту тізбектерінің көмегімен жоғарылатылады.

Бетатронның жұмысы электромагниттік индукция құбылысына негізделген. Егер тұйық орам қамтитын магнит ағыны өзгерсе, онда ол орамда

$Е = - \frac{dФ}{dt}$ (2. 6)

электр қозғаушы күш пайда болады. Егер орамның орнына ауасы сорылған, ішінде еркін қозғала алатын зарядталған бөлшектер бар, түтік қойылса, онда тұйық траекторияны өткен зарядталған бөлшектің энергиясы

$\mathrm{\Delta}W = qE = - q\frac{dФ}{dt}$ (2. 7)

өзгереді. Бөлшек радиусы r шеңбер бойымен қозғалу үшін, магнит өрісі

$P = qB$ (2. 8)

шартын қанағаттандыруы керек. Ал, электр өрісіндегі бөлшектің импульсы

$\frac{dP}{dt} = qE$ (2. 9)

формуласымен анықталады. Егер түтік ішіндегі өріс біркелкі болса,

$E = + \oint_{}^{}{Edl = E \bullet 2\pi r = - \frac{dФ}{dt}}$ (2. 10)

(2. 8) -(2. 10) өрнектерінен бөлшек үдетілетін, радиусы R стационар орбита үшін, магнит өрісінің индукциясы

$В_{орб} = \ \frac{Ф(t) }{2\pi R^{2}}$ (2. 11)

болады. Екінші жағынан бұл орбита қамтитын аудан арқылы өтетін магнит ағыны

$Ф(t) = \pi R^{2}B_{орт}$

болатынын ескерсек,

$В_{орб}\ = \ \frac{1}{2}В_{орт}$ (2. 12)

шығады. Мұндағы В _орб -зарядталған бөлшектің орбитасындағы магнит өрісінің индукциясы, $В_{орт}$ - осы орбита қамтитын аудан үшін магнит өрісі индукциясының орташа мәні (2. 12) шартын 2:1 шарты дейді.