Қатпарлы серпімді бет теңдеуінің математикалық моделін жасау технологиясы мен пайдалану әдістемесі


КІРІСПЕ
Зерттеудің көкейкестілігі.
Ғылымның және техниканың дамуы, жаңа құрылыстарды құрушы болашақ мамандар, ғылыми-техникалық прогрессияның жоғарылау деңгейіне жауап беретін, қатпарлы серпімді бет теңдеуінің математикалық моделін жасау технологиясын пайдалану болып табылады.
Нақты қолданбалы есептер және механикадағы деформацияланатын қатты дене зерттелуінің даму заңдылығы жарық көруде. Мұның толық есебі үшін материалдардың физика-механикалық қасиеті, уақыт бойынша олардың деформацияланатын сипаттамасы, температуралы, электрлі және магнитті жолдардың механикалық деформацияланатын жолдарының өзара байланыс эффектілерінің, денелердің геометриялық тұрғызылуының дамуы болып табылады.
Берілетін зерттеудің нәтижесінде стационарлы, стационарлы емес, тербелмелі және толқынды процестердің қарастырылуы, деформацияланатын қатты дененің механикасы, құрылыс механикасы, гидродинамика, геофизика ғылымдарының бөлімдерінде жақсы жетістіктерге алып келеді.
Болашақ еліміздің құрылысшы, сәулетші мамандығын игеруші мамандарға жоба жасау кезінде құрылыстың ұзақ сақталуына, сенімділігін қамтамасыз етуіне және материалдық ресурстарды тиімді пайдалануға аса қажетті болып табылады.
Зерттеудің мақсаты:
Құрылысшы мамандар даярлау негізінде студенттердің таңдау курсы ретінде ұсынылатын «Қатпарлы серпімді бет теңдеуінің математикалық моделін жасау» технологиясы мен пайдалану әдістемесін жасау
Зерттеу нысаны:
Қатпарлы серпімді бет теңдеуінің математикалық моделін жасау технологиясы мен пайдалану әдістемесін жасау
Зерттеудің әдістері:
-математикалық амалдар негізінде шағын деформация теңдеулерін шешу әдістері;
-компьютерлік графиканың қолданылу аймағы, ғылыми графика.
-Mathcad пакетін қолданып инженерлік есептеулерді жүргізу әдістері.
- Maple жүйесінде математикалық графикаларды модельдеу әдістері.
Зерттеудің ғылыми жаңалығы және теориялық мәні:
-қолданбалы есептер және механикадағы деформацияланатын қатты дене зерттелуінің даму заңдылығы анықталды;
-серпінді және байламалы - серпімді динамикасының негізгі есептері түрлендірілді;
-құрылыс конструкцияларындағы қолданылатын материалдардың, серпінді және байламалы - серпімді қасиеттері анықталды.
Зерттеудің практикалық маңыздылығы:
- құрылыс конструкцияларындағы деформацияланатын орта есебін шешудің әдіс-тәсілдері белгіленді;
- құрылыс конструкцияларындағы деформацияланатын орта есебінің тәжірибелік мүмкіндіктері табылды.
Жұмыс құрылымы мен көлемі:
Диссертация кіріспеден, төрт тараудан, қорытындыдан, пайдаланылған әдебиеттер тізімінен тұрады.
НЕГІЗГІ БӨЛІМ
Кіріспе бөлімінде зерттеудің көкейкестілігі, зерттеу мақсаты, зерттеу әдістері, зерттеудің ғылыми жаңалығы, жарық көрген мақалалар сипатталып көрсетіледі.
Бірінші бөлімде ғылым мен техниканың дамуына қарай педагогиканың да мүмкіншіліктері артқандықтан, жаңа технологиялар пайда болуып, қазіргі кезде оқу ақпараттың ауқымды кең тараған формасының бірнеше түрлері негізінде оқу процесін ұйымдастыру жайлы мәселе қозғалып, жоғары оқу орындарында жаңа курстар құру мен дамыту объектісі және оқу құралы ретінде қатысатын түрлі компьютерлік құралдарды қолданумен тығыз байланыстылығы айтылды. Ақпараттандыру құралдарының сапасынан моделдер жасауды оқытудың тиімділігі тәуелді болатынын және жаңа курстарды оқытудың құралы ретінде білім беруде математикалық моделдерді қолданумен жүзеге асырылатын оқыту әдістемесі ерекше рөл атқаратындығы зерттеліп, осы тақырыпқа зерттеу жүргізгенде, модель жасауда жаңа технологиялардың қалыптасу және құрылу тәсілдерін игеру керек екендігі көрсетілді.
Электрондық ресурстарды жасау және қолданудың анықталған тәжірибелері Қазақстанда да жинақталған. Е. Ы. Бидайбеков, К. М. Беркінбаев, С. С. Үсенов жасаған еңбектері бар. Бірақ олардың зерттеулері жаңа ұрпақтың оқу-әдістемелік кешеніне арналған және таңдау компаненті бойынша оқытудың мәселелері қарастырмайды.
ТМД-ның көптеген басқа елдеріндегі сияқты, республикада үздіксіз білім беру жүйелерінің барлық сатыларында жаңа ақпараттық және телекоммуникациялық технологияларды қолдануға арналған құралдарды енгізу мен құруды алдына мақсат етіп қойған коммерциялық кәсіпорындар мен шығармашылық топтар көбейіп келе жатыр. Бірақ жасалған құралдар бір-бірімен байланысты емес, әртүрлі ерекшеліктер мен әдістерге сәйкес құрылып отыр. Педагогикалық бағытта құрылған көптеген компьютерлік құралдар педагогикалық, психологиялық және басқа да талаптарға жауап бере алмайды.
Осыған байланысты, таңдау компаненті негізінде ғылыми-әдістемелік, технологиялық және ұйымдастырушылық қалыптастыру негіздері, сапа мониторингі және практикалық қолданудың мемлекеттік деңгейде жасау өзекті мәселе болып отыр.
Оқытудың бұл түрі педагогикалық қызметтің тиімділігін көтеруде ерекше рөл атқарады. Осыған байланысты, берілген сала бойынша жүзеге асатын ғылыми-әдістемелік және технологиялық өңдеулер мен басылымдар жоғары деңгейлі өзекті және практикалық мәнділікке ие болып отыр. Ғылыми еңбектер және олардың негізінде ғылыми-негізделген ережелер жүйесін қалыптастыру, жасау және мониторинг тәртібін, білім беру электрондық сапасын, зерттеушілер мен оқытушылар қатарын талдайтын жүйе керек. Бұл жүйенің бөліктері жоғары кәсіби білім беру жүйесін дамытуды және қолдауды қамтамасыз ететін құралдарды жасаудың республикалық және аймақтық өзекті жобаларын қалыптастыруда қолданылуы мүмкін.
Екінші бөлімде техникалық жоғары оқу орындарының (ЖОО) профессорлық-оқытушылық орталарында білім үрдісіндегі компьютерлік математиканың біртұтастығы жайлы жиі талқыланып жатқан мәселелер, тек техникалық бағытқа ғана қатысты емес, сонымен қоса гуманитарлық бағытта да қолданылуының маңыздылығы жайлы сөз қозғалады. Себебі компьютерлік математика жүйесін гуманитарлық және жаратылыстану бағытындағы мектеп оқушыларына информатикадан факультатив сабағында оқытудың өзі оқушыларға ғылымға деген қызығушылығын арттырады.
- Компьютерлік математика жүйесін білім үрдісіне енгізудің проблемасы білім берудің осы дәстүрлі жүйесінің жағдайынан туындайтын сұрақтарды қозғайды. Дәл осы период бойынша, отандық білім беру жүйесінде, объективті түрде білім сапасын көтеруге оң және теріс әсер ететін факторлар аталды.
Қолданбалы тапсырмаларды шешу кезінде, бүкіләлемдік мамандар компьютерлік математиканың программалық жүйесінің MathLAB Mathematica, MathCAD, Maple жан-жақты типін кең ауқымда пайдаланады. Бұл жүйелерді білу дәл, нақты нәтиже алуды жеңілдетеді, оны графикалық түрде ұсыну, есеп берулерді көркемдеу және т. б. ЖОО білім процесінде мына жайттарды еске ала отырып туындаған мүмкіндіктерді ұтымды пайдалана білуі тиіс: бітірушінің болашақ кәсіби қызметі, оның дербес компьютерді кең ауқымда қолдана алатындығында, кеңейтілген программалық палитралар мен аппараттық орталарды игеруінде екенін көрсеткен.
Қажеттілігі мен жеткіліктілігінің арқасында компьютерлік математика жүйесі білім үрдісіне толықтай енгендіктен, бірінші ЖОО-да компьютерлік математика жүйесі студенттердің алғашқы курстарында көп көңіл аударылуы керектігі, осыдан кейін ғана компьютерлік математика жүйесін нәтижелерді тексеру үшін қолдануға болатыны атап айтылды.
Барлық жағдайға арналған ыңғайлы құрал ретінде Mathcad жүйесін атап көрсетуге болады. Төменде 1- суретте бұл жүйенің қарапайым құжаты notebook (блокнот) стилінде көрсетілген, онда анықталған интегралдарды есептеудің геометриялық мағынасы келтірілген. Интегралдарды шешудің қарапайымдылығы және нәтижені Mathcad жүйесінің құралдарымен сандық және аналитикалық түрде алуға болады.
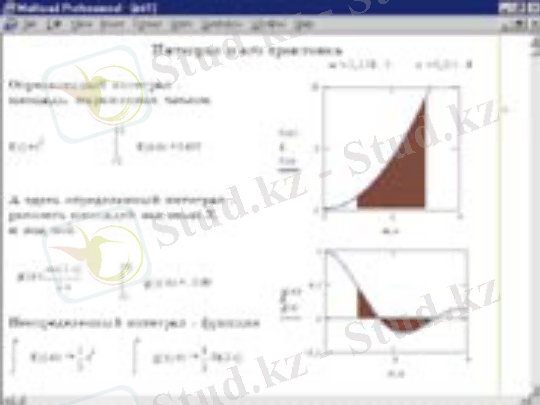
Мысалы, білім беру саласында геометрия сабағында үшөлшемді кеңістікті, әсіресе кескіндердің кеңістікте орналасуын және өзара қиылысуын қабылдау оқушыларға қиынға соғады. Бір кеңістікте бірнеше графикті тұрғызудың өзі көп уақытты алады.
Барлық компьютерлік математика жүйелері екі және үш өлшемді графиктерді тез және оңай тұрғызады. Тек қана кеңістік биіктігін матрицалық тұрғыда беріп, қажетті график салу құралдарын таңдасақ жеткілікті. Мұндай құралдардың ішінде кеңістікті бояу, жарықтық эффектілер, кеңістіктің орналасуын таңдау және т. б. эффектілер кіреді. Көптеген жүйелер (Mathcad немесе Maple) үш өлшемді графикті тышқанның көмегімен айналдыру арқылы фигураны ыңғайлы көруге мүмкіндік алады және қарапайым тұрғызылады.
2-сурет Кеңістікте қиылысатын үш өлшемді графиктерді тұрғызу (Mathcad жүйесі) .

Ұзақ уақыт бойы математикалық программалар (Eureka, Mercury, Mathcad және Matlab программаларының ескі нұсқалары) сандық есептеулер мақсатында дамыды. Бірақ жиырмасыншы ғасырдың тоқсаныншы жылдары символдық математика (компьютерлік алгебра) жүйелері тез дами бастады. Оларға аналитикалық есептеулердің интегралды түрлері, мысалы функцияның шектерін табу және олардың туындылары, анықталған және анықталмаған интегралдарды есептеу, функцияны тізбекке жіктеу, орналастыру және комбинациялау және т. б. операциялар жатады.
Mathcad-та сандық және символдық массивтерді қолдану алдын-ала қаралған. Массивтер бір өлшемді және екі өлшемді болып келеді. Екі өлшемді массивтер (матрицалар) ұзындығы бірдей бір өлшемді массивтердің жиынтығы ретінде қарастырылады. Бір өлшемді массивтер вектор жолдар және вектор-бағаналар болуы мүмкін.
Құжатқа матрица кірістіру үшін вектор және матрица панелін (vector and matriv toolbar) шығарып, содан соң матрица шаблонын (matrix or vector) таңдаймыз. Сондай-ақ Insert (Кірістіру) менюінен Matrix (Матрица) командасын пайдалансақ немесе Ctrl+M батырмасын бассақ жеткілікті.
3- сурет Матрица панелі
Матрица мен векторларды енгізу үшін матрица панелін басу арқылы Insetrt Matrix (матрицаны енгізу)
 терезесін шақырсақ болады. Сол кезде бізге төмендегі терезе ашылады:
терезесін шақырсақ болады. Сол кезде бізге төмендегі терезе ашылады:
4- сурет Матрицалар мен векторларды енгізу шаблоны

Екі өлшемді графикті f(x) функциясы үшін жеңілдетілген түрде тұрғызу үшін оның шаблонын шығарып, вертикаль ось бойынша - функцияны көрсетіп, ал горизанталь ось бойынша - тәуелсіз айнымалыны көрсетеміз. Осы арқылы кез-келген бір суретте бірнеше графикті тұрғызу үшін у осіне үтір арқылы бірнеше функцияларды енгізу қажет. Графиктер әр түрлі типті және түсті сызықтармен көрсетіледі.
Сонымен қатар бірінші функцияны жазып алып, одан кейін (курсорды функциялар облысында қалдырып) графиктердің шаблонын шығаруға болады; функция у вертикаль осінде жазылып қалады және у горизанталь осіне қатысты тәуелсіз айнымалыны көрсету жеткілікті.
5-сурет Декарттық координата жүйесіндегі график.

Қарапайым әдіс бойынша графикті құру тәуелсіз айнымалының -10 нан +10 - ға дейінгі мәндер аралығында тұрғызылады. Бұл диапазонды форматтауға және графиктің басқа да параметрлерін өзгертуге болады. Құрылған графиктің параметрлерін беру үшін оны белгілеп диалогтық терезеден 3 әдістің біреуін таңдайды:
Үшінші бөлімде Maple бағдарламасының көмегімен құрылыс конструкцияларындағы қатпарлы пластинкалардың графиктері сызылып, моделдері құрылады. Maple жүйесінде бірнеше функциялардың графиктерін сызу мүмкіндігі бар. Мұндай жағдайда графиктерді бір-бірінен ажыратып көрсету үшін оларды әр түрлі стилде сызу мүмкін. Бұл мүмкіншіліктен мысалы графиктерді экранға немесе қағазға шығарғанда пайдалануға болады. Егер графикті сызған кезде style параметрін пайдалансақ, онда сызықтың түрлерін style параметрінің төмендегі:
POINT немесе point - график нүктемен шығарылады;
LINE немесе line - график тұтас сызықпен шығарылады.
мәндерімен анықтауға болады
Сolor атты параметр жәрдемінде график сызықтарының әртүрлі түстерін таңдауға болады .
Бір қатпарлы пластинкалардың графигін тұрғызған кезде ол функция plot бұйрығында f тың орнында анық көріністе жазылу керек. Мысалы үшін:
sin(x) /x функция графигін сызу
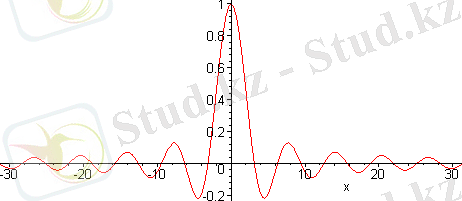
Бұл графикте сызықты басқа түрде шығаратын болсақ, мысал үшін қалын сызықпен онда мынандай жағдай болады
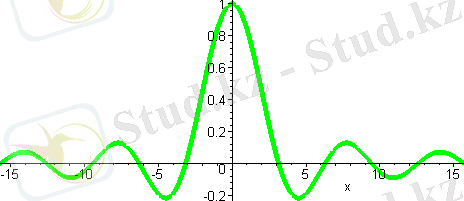
Мұндағы thickness=5 параметр график сызығын 5 рет қалын етіп сызады.
Егер функция графигін х →∞ болғанда сызу керек болса, онда
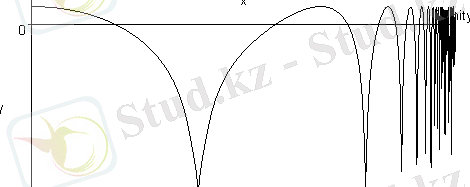
Үзіліске ие функциялардың графигін сызып көрейік. Мысалы үшін tan(x) графигін сызатын болсақ, онда
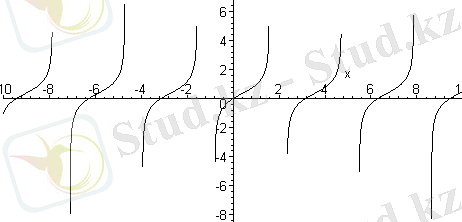
Үзіліске ие функциялардың графигін сызған кезде олардың графигі кейде жақсы сызылмауы мүмкін. Сондай кезде plot бұйрығының discont атты параметрін қолданған жөн. Мысалы:
plot(ln(1+tan(x) ), x=-10. . 10, color=black, discont=true) ;
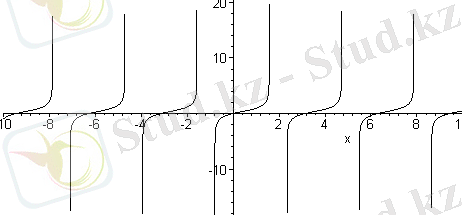
Егер бұл параметрдің мәні false болса, онда кәдімгі жәй графиктер сызылады.
Бірнеше қатпарлы пластинкалардың графигін бір жерде шығару мысалын қарастырайық. Мұндай графиктерді сызу үшін бұл функциялардың аттары жазылып, олардың аргументтерінің өзгеру интервалы көрсетіледі. Мысалы үшін
plot([10*sin(x), x^2, cos(x) ], x=-10. . 10, y=-10. . 10) ;
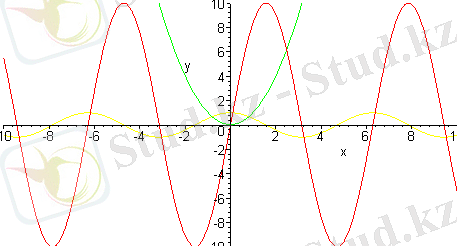 Әдетте графиктер әртүрлі түсте боялады. Бірақ бұл пайдаланушыға әрдайым дұрыс келмейді. Сол себептен color (сызық түсі) және style (сызық стили) параметрлерінен пайдалана отырып, сызықтардың көрінісін жақсыласа болады.
Әдетте графиктер әртүрлі түсте боялады. Бірақ бұл пайдаланушыға әрдайым дұрыс келмейді. Сол себептен color (сызық түсі) және style (сызық стили) параметрлерінен пайдалана отырып, сызықтардың көрінісін жақсыласа болады.
Негізі бірнеше функциялардың графиктерін бір жерден шығарудың өте қажетті жерлеріде бар: Мысалы функцияны полиномдармен апрокцимацияласақ онда функция графигін және полином графигін бір жерде көре отырып, біз жуықтаудың қателік дәрежелерін үйренуімізге болады.
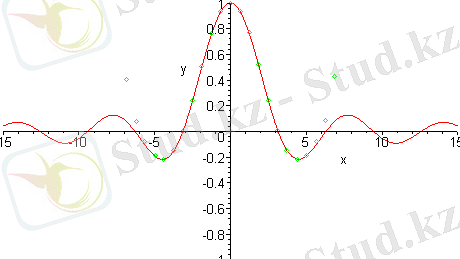
Бұл графиктен sin(x) /х функцияны жуықтаушы полином 0 нукте төңірегінде сол функциямен бірдей екендігі көрініп тұр.
Кейінгі мысалда элементар функциялардың комбинацияларынан құрылған функциялардың графиктері қарастырылған.
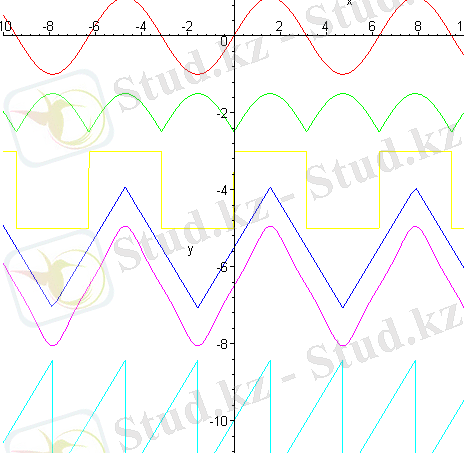
Бұл сияқты элементар функциялардың қосындысы сигналдарды моделдеуші периодты функциялар графиктерін құруға мүмкіншілік береді.
Жоғарыда қарастырылған полином графигі нүкте белгілерімен сызылған еді. Бұл полиномның сол нүктелерде ғана анықталғанын білдірмейді. Бұл жерде сызықтың стилі жақсы таңдалған. Көп жағдайда функциялардың мәндері кейбір нүктелермен ғана берілуі мүмкін, олардың графигін сызу жағдайын қарастырайық. Мұндай жағдай функцияның мәндері эксперименттерде анықталып, олар дискрет мәндер болуы мүмкін.
Төменде осы сияқты функция графигі сызылған .
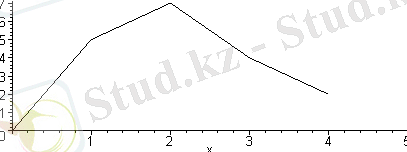
Немесе
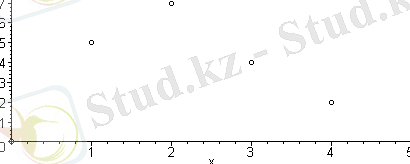
Maple жүйесінің тағыда бір ғажайып мүмкіндігі - функция өзінің функционал атымен ғана берілгенде графигін сызу. Мұнда функцияның аргументтері түралы мәлімет берілмейді. Осы мүмкіндікті бірнеше функцияның графигін бір суретте сызып корсетейік.
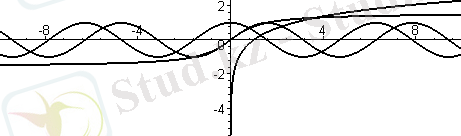
Бұл мысалдан көрініп тұргандай графикті сызған кезде plot бұйрығында диапазондарды көрсетудің қажеті жоқ екен. Мұнда горизонталь осьтың диапазоны -10. . 10, ал вертикаль осьтың диапазоны функцияның өзгерісіне қарап, автоматты түрде қабылданады екен.
Егер де функция вектор түрінде берілген болса онда графикті сызу мысалы төмендегідей болады.
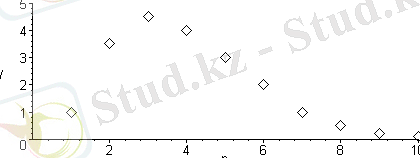
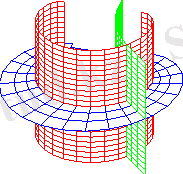
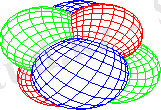
coordplot3d(rectangular)
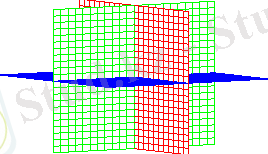
coordplot3d(paraboloidal, labelling=true)
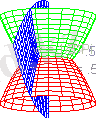
infolevel[coordplot3d] :=2:
coordplot3d(rosecylindrical)
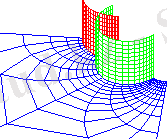
coordplot3d(sixsphere)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz