Жылуөткізгіштік теориясы және айырым схемалар: теңдеулер, бастапқы-шекаралық шарттар және сандық әдістер


Мазмұны
Кіріспе
Жылу өткізгіштік теориясының негіздері . . . 3
Негізгі бөлім
а) Жылуөткізгіштік теңдеуі . . . 8
ә) Айырым схемалары теориясының негізгі ұғымдары . . . 16
б) Айырым схемасының ұқсастығы, аппроксимациясы
және орнықтылығы . . . 28
с) Айқын және айқын емес айырым схемалары . . . 32
Қорытынды . . . 34
Қолданылған әдебиеттер тізімі . . . 35
Кіріспе
Жылу алмасу процестерінің теориясы
Заманауи технология мен техниканың көптеген процестерін шешуге байланысты жылу тасымалы процессі заманауи физиканың түсініктеріне сәйкес екі көзқарас тұрғысынан зерттеледі және сипаталады. Олар феноменологиялық және статистикалық зерттеу тәсілдері. Феноменологиялық және статистикалық тәсіл қарастырылатын физикалық құбылысты тұтасымен анықтайтын параматрлердің арасындағы кейбір жалпы қатынастарды анықтауға негізделеді. Бұл зерттеу тәсілінде негізгі мәселе

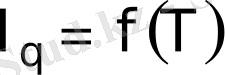
түріндегі байланысын құруға келіп тіреледі. Мұндағы U-потенциал, I-ағын. Бұл байланыстың жалпы сипаты жылу тасымалданудың үш мүмкін түрінің бірімен анықталады.
Оларды біріншісі - жылуөткізгіштік жылу энергиясын физикалық жүйенің микроскопиялық элементерімен (молекулалар, иондар, электрондар) тасымалдануға қатысты. Газдардағы жылуөткізгіштік энергияны молекулалар соқтығысу арқылы, қатты денеде зат торының тербелген иондарымен және “электрондық газбен”, сұйықта - көрсетілген барлық механизмдермен іске асырылады.
Микроскопиялық көлемінің қозғалысы есебінен іске асатын жылу берілу конвекция деп аталады. Конвекцияның екі түрі бар --массаның элементтері жүйе көлемінің тығыздықтарының әртүрлі болуынан ауырлық күші өрісінде орын ауыстырғандағы еркін конвекция, және массасының орын ауыстыруы сыртқы күштердің есебінен іске асырылатын мәжбүр конвекция деп аталады.
Жылу алмасудың үшінші түрі - сәулелену денелердің электромагниттік өрістің энергиясын жұтуына, шағылуына, өткізуіне және сәулелендіруіне негізделген.
Феноменологиялық заңдар жалпы сипатта, ол нақты физикалық ортаның ролі пропорционалдық коэффициентері - сонымен бірге эксперименталді анықталатын коэффициенттермен бірге ескеріледі.
Жылу тасымалдану процесстері жылуөткізгіштікпен іске астын физикалық жүйені қарастырайық. Феноменологиялық термодинамиканың жалпы процедуралалына сәйкес мұндай жүйені зертеуді біз энтропия көзі үшін өрнек жазудан бастаймыз. Энтропия көзінің интенсивтілігі үшін жалпы өрнекпен, келесіні аламыз:
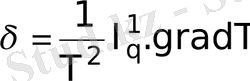 (1)
(1)
жүйеде жылу өткізгіштік құбылыстар жүрмейтіндіктен, диффузия процестері жоқ, I q және I q 1 жылу ағындары сәйкес келеді. (1) теңдеуге негіздеп, жылуөткізгіштік құбылысы үшін термодинамикалық күштер мен ағындарды енгізуге болады. Бұл жағдайда бұлай болу айқын:
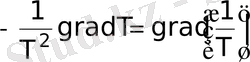 термодинамикалық күш;
термодинамикалық күш;
I q - термодинамикалық ағын.
Феноменологиялық термодинамика бұдан ары енгізілген термодинамикалық күштер мен ағындардың арасында қандайда бір сызықтық қатынас болуы керек деп тұжырымдайды (феноменологиялық заң) :
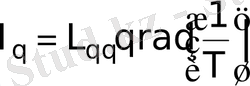 (2)
(2)
Бұл феноменологиялық заң келесідей түрде жазылуы мүмкін:
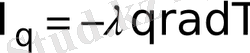 (3)
(3)
мұндағы
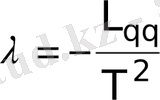 (4)
(4)
(4) қатынасты 1822ж эксперимент жүзінде тұжырымдарды және Фурье заңы деп аталады.
(4) өрнектегі тасымалданудың феноменологиялық коэффициентінің бірі болатын пропорционалдық коэффиенциент жылу өткізгіштік коэффициенті деп аталады. Бұл коэффициент қарастырылатын жүйенің физикалық қасиеттерін ондағы өтіп жатқан жылуөткізгіштік процессі тұрғысынан қарастырылады. Құбылысты
феноменологиялық сипаттағанда жүйенің барлық физикалық қасиеттері, басқаша айтқанда физикалық жүйелердің бір-бірінен ерекшелігі тек тасымалдау коэффициентері арқылы көрсетіледі. Көптеген сипаттау экспериментпен жоғары дәлдікпен келеді.
Екі жағдайларды қарастырамыз (1-сурет) . Оның біріншісінде (изотопты орта, 11-сурет),
 жылуөткізгіштік коэффициентінің шамасы бағытқа тәуелді емес. I
q
жылу ағыны Фурье заңына сәйкес, нормальға қарама-қарсы изотермаларға (температура градиенті) бағыталған, екінші жағдайда - анизотропты орта (1б сурет) - құбылысы күрделірек. I
q
- жылу ағынының бағыты жылуөткізгіштік тензорымен анықталады, бұл жағдайда
жылуөткізгіштік коэффициентінің шамасы бағытқа тәуелді емес. I
q
жылу ағыны Фурье заңына сәйкес, нормальға қарама-қарсы изотермаларға (температура градиенті) бағыталған, екінші жағдайда - анизотропты орта (1б сурет) - құбылысы күрделірек. I
q
- жылу ағынының бағыты жылуөткізгіштік тензорымен анықталады, бұл жағдайда
 коэффициенті анықталады, бұл жағдайда
коэффициенті анықталады, бұл жағдайда
 коэффициенті, оған сай I
q
ағын ең үлкен және ең кіші мәндерге ие болатын бағыттар бар.
коэффициенті, оған сай I
q
ағын ең үлкен және ең кіші мәндерге ие болатын бағыттар бар.
Жылуөткізгіштік тензоры - екінші ранглі тендор - келесідей жазылады
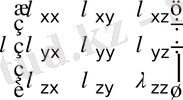 (5)
(5)
(3) өрнекпен берілген Фурье заңы тензорлық түрде координаталар остеріне проекцияланып скаляр түрде келесідей жазылады:
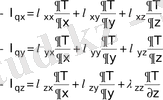 (6)
(6)
(6) қатынасты координата остеріндегі түйіндес әсерлермен байланысққан жылу ағындарының проекцияларын байланыстаратын қатынас ретінде қарастыруға болады, яғни анизатропты денеде х осі бойынша жылу ағыны у және х осьтері бойынша температураның түсуіне, немесе керісінше у осіндегі температураның кемуі қалған х және у осьтері бойынша температураның кемуіне әкеледі.
Бұл көзқарас тұрғысынан жүйенің (6) теңдеудекгі коэффициентері феноменологиялық термодинамика тұжырымдағандай Онзагердің қатынастарына бағынуы керек. Яғни сәйкес түйіндес коэффициентер тең болуы керек
 және т. с. с.
және т. с. с.
(7) қатынас
 тензорының симметриялық шарты болып табылды. Осылайша Онзагер қатынасынан жылуөткізгіштік тензорының - симметриялық тензор екендігі шығады. Жылуөткізгіштің бұл тензорын экспримент жүзінде Соре и файгт тетрагокальді класстың кристалдарының жылуөткізгіштіігін зерттегенде, тексерді.
тензорының симметриялық шарты болып табылды. Осылайша Онзагер қатынасынан жылуөткізгіштік тензорының - симметриялық тензор екендігі шығады. Жылуөткізгіштің бұл тензорын экспримент жүзінде Соре и файгт тетрагокальді класстың кристалдарының жылуөткізгіштіігін зерттегенде, тексерді.
Осылайша, жылу ағыны мен арасындағы жалпы феноменологиялық қатынасты қарастыра отырып, анизотропты орта жағдайында ағын және векторлар бірдей бағыт алмайтындығын; олардың арасындағы байланыс (6) қатынаспен анықталатындығы жөнінде тұжырым жасауға болады. Тек изотропты жүйе жағдайында жылуөткізгіштік тензоры скалярға келіп және жылу ағыны мен
 бағыты сәйкес келеді. Жылуөткізгіштік процессін жалпы сипатағанда, ортаның анизотроптылығын ескеру математикалық қиындықтар туғызады. Техникалық маңызды материалдардың көпшілігін бірінші жуықтауда изотропты деп, ал олардың жылуөткізгіштік коэффициентерін скаляр деп санауға болады.
бағыты сәйкес келеді. Жылуөткізгіштік процессін жалпы сипатағанда, ортаның анизотроптылығын ескеру математикалық қиындықтар туғызады. Техникалық маңызды материалдардың көпшілігін бірінші жуықтауда изотропты деп, ал олардың жылуөткізгіштік коэффициентерін скаляр деп санауға болады.
а) ЖЫЛУӨТКІЗГІШТІК ТЕҢДЕУІ
Біз мұнда жылуөткізгіштік теңдеуін “классикалық” қорытамыз. Сақталу заңдарының бірінің теңдеуін (энергияның сақталу заңы) және Фурье заңын қолданамыз. Жылуөткізгіштік теңдеуін энергияның сақталу заңының теңдеуімен Фурье теңдеуінен тұратын жүйенің математикалық эквиваленті ретінде қарастырамыз.

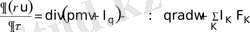 (7)
(7)
Энергияның сақталу заңының теңдеуін қолданамыз. Бұл жағдайда жүйенің массалар центрінің өзгерісі жоқ деп, яғни w=0 деп қарастырамыз. Бұл жағдайда (7) теңдеу ықшамдалады, келесі түрге келеді:
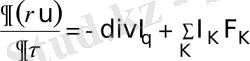 (8)
(8)
Тек жылуөткізгіштік процесін қарастырғанда оң жақтағы соңғы мүшесін терең қарастырамыз, тек қандай да бір энергияның (немесе жылудың) бөлінуі маңызды.
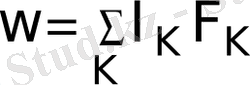 (9) белгілейміз.
(9) белгілейміз.
Жүйенің ішкі энергиясы u тек оның температурасына тәуелді деп есептейміз. Идеал осылайша, жылусыйымдылық деп сол сыртқы параметрлерде жүйенің ие болатын жылу сыйымдылығын аламыз. Осылайша,
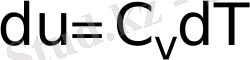 (10)
(10)
Мұндағы
 -сыртқы параметрлердің белгілі бір мәніндегі жылусыйымдылық.
-сыртқы параметрлердің белгілі бір мәніндегі жылусыйымдылық.
Егер (8) теңдеудегі жылу ағынын (3) теңдеуге сәйкес өрнектесек және (9, 1) теңдеулерді қолдансақ, келесіні аламыз:
 (11)
(11)
(11) теңдеу жылуөткізгіштік теңдеуінің неғұрлым жалпы математикалық жазбасы.
Жалпы жағдайда
 жылуөткізгіштік коэффициенті тензор, және осылайша оң жақтағы бірінші мүше тензорды векторға көбейту ережесіне сәйкес келесідей жазылады.
жылуөткізгіштік коэффициенті тензор, және осылайша оң жақтағы бірінші мүше тензорды векторға көбейту ережесіне сәйкес келесідей жазылады.

(12) өрнек келесідей жеке жағдайлар ықшамдалады:
1. Қарастырылатын жүйе изотропты, және осылайша
 жылуөткізгіштік тензоры скаляр. Онда
жылуөткізгіштік тензоры скаляр. Онда
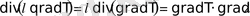 (11) өрнек келесідей түрге келеді:
(11) өрнек келесідей түрге келеді:
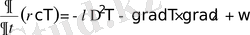 (12)
(12)
мұндағы
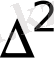 - Лаплас операторы, ал
- Лаплас операторы, ал
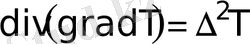 (13)
(13)
Жылуөткізгіштік коэффициенті координаталарға, ал тығыздық пен жылусыйымдылық уақытқа тәуелсіз десек, жылуөткізгіштік теңдеуі келесі түрге келеді:
 (14)
(14)
мұндағы
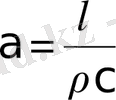 - Максвелл бойынша жылуөткізгіштік коэффициенті немесе Кельвин бойынша жылу диффузиясының коэффициенті:
- Максвелл бойынша жылуөткізгіштік коэффициенті немесе Кельвин бойынша жылу диффузиясының коэффициенті:
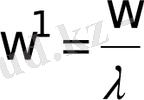 .
.
Стационар процестер үшін жылуөткізгіштік теңдеуі Пуассонның әдеттегі теңдеуіне келеді:
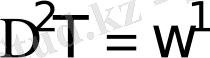 .
.
Ішкі жылу көздері болмаса, (14) теңдеу Лаплас теңдеулеріне келеді:
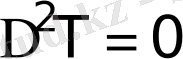
2. Жылуөткізгіштік тензорының компонентері координаталарға тәуелсіз. Магнит өрісі жоқ. Бұл жағдайда (12) өрнек келесідей түрленеді: (15)
 Екінші ретті дифференциал теңдеулердің теориясында көрсетілгендей, өрнектің оң жағына координаталарды ауыстыру арқылы аралас туындыларды жойып, келесі түрге келтіруге болады:
Екінші ретті дифференциал теңдеулердің теориясында көрсетілгендей, өрнектің оң жағына координаталарды ауыстыру арқылы аралас туындыларды жойып, келесі түрге келтіруге болады:
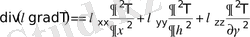
мұндағы
 - жаңа төртбұрышты координаталар. Алынған жағдай үшін жылуөткізгіштік теңдеуі келесідей жазылады:
- жаңа төртбұрышты координаталар. Алынған жағдай үшін жылуөткізгіштік теңдеуі келесідей жазылады:
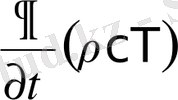
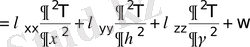 (17)
(17)
енгізілген жаңа координаталар (
 ) жүйесін
бас жүйе
, ал оның остерін жылуөткізгіштіктің
негізгі остері
деп атаймыз. (17) теңдеуді тағы да ықшамдаймыз, ол үшін координатаны тағы да түрлендіреміз:
) жүйесін
бас жүйе
, ал оның остерін жылуөткізгіштіктің
негізгі остері
деп атаймыз. (17) теңдеуді тағы да ықшамдаймыз, ол үшін координатаны тағы да түрлендіреміз:
 (18)
(18)
Мұнда
 шамалары кездейсоқ таңдалып алынды. Жаңа координаталарда (17) теңдеу келесідей жазылады:
шамалары кездейсоқ таңдалып алынды. Жаңа координаталарда (17) теңдеу келесідей жазылады:
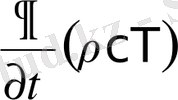
 (19)
(19)
ә) БАСТАПҚЫ ЖӘНЕ ШЕКАРАЛЫҚ ШАРТТАР
Жылуөткізгіштің дифференциалдық теңдеудің жалпы жағдайда көп шешімдері болады. Бұл жиының ішінен нақты қарастырылған процессті бірмәнді сипаттайтын жауапты алу үшін негізгі теңдеуге қосымша шарттарды қосу керек. Бұл шарттар тікелей экспериментпен анықталады, немесе эксперимент мәліметтерін жалпылау арқылы табылады.
Дифференциал теңдеудің шешімі деп, теңдеуді тепе-теңдікке жалпылайтын және осы қосымша шарттарды қанағаттандыратын
 функциясын аламыз. Шешімнің графигі төртөлшемді кеңістіктегі қандайда бір бет болып табылады (интегралдық бет) . Мұндай интеграциялауда қарапайым шекаралық шарттар
функциясын аламыз. Шешімнің графигі төртөлшемді кеңістіктегі қандайда бір бет болып табылады (интегралдық бет) . Мұндай интеграциялауда қарапайым шекаралық шарттар
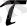 уақыт жазықтығы мен x, y, z координаталық беттермен жазықтықтың қиылысқандығы
уақыт жазықтығы мен x, y, z координаталық беттермен жазықтықтың қиылысқандығы
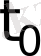 функциясын беру болып табылады. Соңғылары, бастапқы шарттар, алғашқылары шекаралық шарттар деп аталады. Себебі олар бастапқы
функциясын беру болып табылады. Соңғылары, бастапқы шарттар, алғашқылары шекаралық шарттар деп аталады. Себебі олар бастапқы
 уақыт мезетінде жүйенің күйін көрсетеді. 2 - суретте
уақыт мезетінде жүйенің күйін көрсетеді. 2 - суретте
екі кеңістік және координаталармен сипатталатын үшөлшемді облыс келтірілген. Жазықтықта бастапқы шарттар
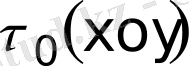 депб ал шекаралық шарттар -
депб ал шекаралық шарттар -
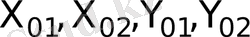 жазықтықтарда беріледі. Фиксирленген уақыт мезетінде (
жазықтықтарда беріледі. Фиксирленген уақыт мезетінде (
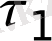 жазықтығы) температуралар өрісі температуралардың
жазықтығы) температуралар өрісі температуралардың
 шек
.
шек
.
 шекаралық мәндерін қоса алғанда
шекаралық мәндерін қоса алғанда
 изотермелар жиынымен беріледі. Кеңістік уақыттың облысқа тән t функциясының үзіліссіздік шарты, сонымен бірге оның туындыларының (біріншісі
изотермелар жиынымен беріледі. Кеңістік уақыттың облысқа тән t функциясының үзіліссіздік шарты, сонымен бірге оның туындыларының (біріншісі
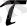 бойынша, екіншісі және біріншісі x, y, z бойынша) шекті жағдайлар үшін орындалмайды. Шектелгенкеңістік облыстарға берілген есептерден басқа, шекті немесе жартылай t шекті облыстар үшін есептер бар. Соңғысына іс-тәжірибеге көптеген маңызды есептер енеді (жылудың жұқа пластинкада таралуы, жылудың ұзын жұқа пластинкада таралуы) .
бойынша, екіншісі және біріншісі x, y, z бойынша) шекті жағдайлар үшін орындалмайды. Шектелгенкеңістік облыстарға берілген есептерден басқа, шекті немесе жартылай t шекті облыстар үшін есептер бар. Соңғысына іс-тәжірибеге көптеген маңызды есептер енеді (жылудың жұқа пластинкада таралуы, жылудың ұзын жұқа пластинкада таралуы) .
Бастапқы және шекаралық шарттардың негізгі типтерін қарастырамыз.
Бастапқы шарттар.
Дифференциалды жылуөткізгішті теңдеу -
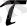 айнымалысы бар бірінші ретті теңдеу болатындықтан, бастапқы уақыт мезетінде келесідей функцияны беру жеткілікті:
айнымалысы бар бірінші ретті теңдеу болатындықтан, бастапқы уақыт мезетінде келесідей функцияны беру жеткілікті:
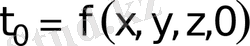 (20)
(20)
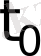 - үздіксіз немесе үзлісті берілуі мүмкін. Егер
- үздіксіз немесе үзлісті берілуі мүмкін. Егер
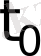 үзіліссіз болса, онда негізгі дифференциал теңдеудің төмендегі шартты қанағаттандыратын t төмендегідей шешім аламыз.
үзіліссіз болса, онда негізгі дифференциал теңдеудің төмендегі шартты қанағаттандыратын t төмендегідей шешім аламыз.
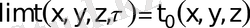 (21)
(21)
Егер
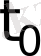 функциясының бастапқы таралуы үзілісті болса, онда аз уақыт аралығынан кейін үзіліс жерлерінде температураның теңдесуі жүреді және t шешім (25, 2) шартты қанағаттандыруы керек.
функциясының бастапқы таралуы үзілісті болса, онда аз уақыт аралығынан кейін үзіліс жерлерінде температураның теңдесуі жүреді және t шешім (25, 2) шартты қанағаттандыруы керек.
Практикада қарапайым бастапқы шартты есептер кездеседі:
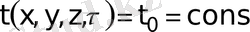 (22)
(22)
жеке алғанда осы жағдайға орныққан режимнен шығуының бастапқы шарттары (“суық” күйден қыздыру, стационар режимдегі жұмыстан кейінгі суыту және т. б) келеді. Бұл жағдайда теңдеуді шешу айтарлықтай жеңілдейді.
Бастапқы шарттарды елемейтін шекті жағдайлар да кездеседі. Мысал ретінде стерженнің ішінде жылудың таралуын қарастырамыз. Егер уақыттың есептік мезеті жеткілікті дәрежеде бастапқыдан алыс болса, онда температуралық өріс іс жүзінде тек шекаралық шарттармен - бастапқы шарттардың ықпалы уақытпен бірге бәсеңдейді. Осылайша, тәжірибе шексіз ұзаққа созылады және бастапқы шарттар керексіз. Осы жағдайда шекарадағы температураның периодты тербелісі келеді, ұзақ уақыт өткен кезде жүйенің нүктелер температурасы шекарадағы температураның тербеліс жиілігіне сәйкес келетін жиілікті заңмен өзгереді. Бастапқы таралуды дәл ескергенде периодты шешім болмайды, әйткенмен, практикаға қажетті дәлдікпен бұл қателіктің ықпалын ескермеуге болады.
Жалпылай айтқанда, кез-келген пішінді денелер үшін бастапқы шарттар тек стационар процесстің бастапқы кезеңі кезеңінде ғана ықпал етеді. Қандай да бір
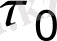 мезетінен бастап, регуляры деп аталған денедегі температураның таралуы бастапқы шарттарға тәуелсіз тек шекаралық шарттармен анықталатын режим орнайды.
мезетінен бастап, регуляры деп аталған денедегі температураның таралуы бастапқы шарттарға тәуелсіз тек шекаралық шарттармен анықталатын режим орнайды.
Шекаралық шарттар
Кейбір типтік шекаралық шарттарды қарастырамыз.
А) Бетте
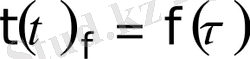 түріндегі функциямен анықталатын температура берілген. Функция қандайда бір
түріндегі функциямен анықталатын температура берілген. Функция қандайда бір
 уақыт аралығында берілген, мұндағы
уақыт аралығында берілген, мұндағы
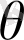 - процесс зерттелетін қандайда бір уақыт аралығы. Облыстың ішінде негізгі теңдеуді қанағаттандыратын және шекарада
- процесс зерттелетін қандайда бір уақыт аралығы. Облыстың ішінде негізгі теңдеуді қанағаттандыратын және шекарада
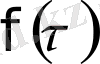 берілген мәнін қабылдайтын
берілген мәнін қабылдайтын
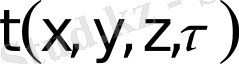 функциясын табу керек болсын. Математикалық физикада бұл есеп бірінші шекті есеп деп, ал Лаплас теңдеуі жағдайында
функциясын табу керек болсын. Математикалық физикада бұл есеп бірінші шекті есеп деп, ал Лаплас теңдеуі жағдайында
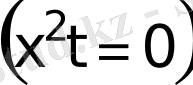 -Дрихле есебі деп аталады. Кейбір жағдайда “бірінші ретті шекаралық шарттар” деп аталады. Бірінші ретті шекаралық шарттарға шекарадағы температураның берілген өзгеруі кезіндегі жүйенің қыздырылуының және сууы жағдайындағы немесе беттегі жылу интенсивті алмасқан кезіндегі есептер жатқызылады.
-Дрихле есебі деп аталады. Кейбір жағдайда “бірінші ретті шекаралық шарттар” деп аталады. Бірінші ретті шекаралық шарттарға шекарадағы температураның берілген өзгеруі кезіндегі жүйенің қыздырылуының және сууы жағдайындағы немесе беттегі жылу интенсивті алмасқан кезіндегі есептер жатқызылады.
Бірінші ретті шекаралық шарттар практикада өте сирек кездеседі, себебі беттің температурасы ізделінді шама болады. Әйткенімен, шектелген асқан интенсивті (мысалы, қайнау, куонденсация, сұйық металдардың мәжбүр тербелісі), жұмыстық ортаның t
ор
температурасы t
бет
беттің температурасына жуықтап тең болатын процесстер кездеседі. Бұл температуралардың айырымы I
q
жылу ағыны және зетттеу мәселесі конвективті жылу алмасу мен фазалық түрленудегі жылу алмасу процесстеріне қарасты болатын
 жылу берілу коэффициентерімен анықталады.
жылу берілу коэффициентерімен анықталады.
 болғанда t
ор
t
бет
. Мысал ретінде, “жылу соққысы” деп аталатын құбылысты қарастырамыз.
болғанда t
ор
t
бет
. Мысал ретінде, “жылу соққысы” деп аталатын құбылысты қарастырамыз.
Мысал ретінде “жылулық соққы” деп аталатын құбылысты қарастырамыз. Суық қабырғаға температурасы
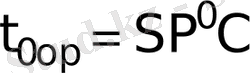 . Қабырғаға соқтығысып бу конденсацияланады
. Қабырғаға соқтығысып бу конденсацияланады
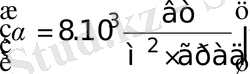 және беттің температурасы тез ортаның температурасына жуықтайды. Бұдан ары ортаның температурасын тұрақты ұстағанда қабырғаның қызуы іске асады.
және беттің температурасы тез ортаның температурасына жуықтайды. Бұдан ары ортаның температурасын тұрақты ұстағанда қабырғаның қызуы іске асады.
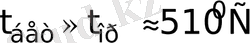
бұл жағдайда қалыңдығы r қабырғадағы температураны есептеу І ретті шекаралық шарттарды қолдану арқылы болуы мүмкін. Температураның шеттік
 таралуы стационар күйге сәйкес келеді. Қарастырылған шекаралық шарттар практикада өте сирек орындалады: ережеге сәйкес нақты денелердің бетінде температуралық өрісті бұрмалайтын контактілік жамылғылар болады.
таралуы стационар күйге сәйкес келеді. Қарастырылған шекаралық шарттар практикада өте сирек орындалады: ережеге сәйкес нақты денелердің бетінде температуралық өрісті бұрмалайтын контактілік жамылғылар болады.
б) Шекарада жылу ағыны берілген (екінші шекаралық есеп, ІІ реттті шекаралық шарттар) .
 (23)
(23)
теңдеуді бұл жағдайда шешу облыстың ішінде негізгі теңдеуді қанағаттандыратын қалыпты туындысы шекарада
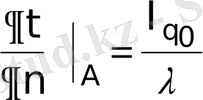 (24)
(24)
Лаплас теңдеуі үшін Нейман есебі деп аталады.
В) Шекарада туынды мен функцияның арасында сызықтық қатынас берілген (үшінші шектік есеп, үшінші текті шекаралық шарттар) ;
 (25)
(25)
бұл шекаралық шарт температурасы берілген ортамен жылу алмасуына сәйкес келеді
 коэффициенті ортаның қабырғамен жылулық әсерлесуінің интенсивтілігін сипаттайды.
коэффициенті ортаның қабырғамен жылулық әсерлесуінің интенсивтілігін сипаттайды.
Лаплас теңдеуі үшін есеп келесідей жазылады:
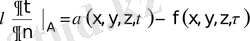
бұл аралас есеп деп аталады:
 Дрихле есебі,
Дрихле есебі,
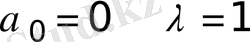 Нейман есебі.
Нейман есебі.
(2) шекаралық шартты өлшемсіз түрге келтіреміз

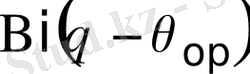
мұндағы
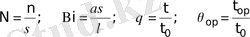

 - тек өлшем,
- тек өлшем,
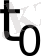 -қандайда бір фиксирленген температура.
-қандайда бір фиксирленген температура.
Ві (Био) критериі ұқсастық теориясында кеңінен қолданылады. Ві
 болғанда үшінші текті шарт бірінші текті шартқа ауысады (үлкен интенсивтегі жылу алмасады қабырғаның тепературасы тең) және бұл жағдай неғұрлым әмбебап болып табылады. Ві=0 жағдайы шекарасында жылулық изоляциясы бар есепке келеді.
болғанда үшінші текті шарт бірінші текті шартқа ауысады (үлкен интенсивтегі жылу алмасады қабырғаның тепературасы тең) және бұл жағдай неғұрлым әмбебап болып табылады. Ві=0 жағдайы шекарасында жылулық изоляциясы бар есепке келеді.
Үшінші текті шекаралық шарттар практикада кеңінен қолданылады (шекарадағы конвективті жылу алмасу)
2) Орта біртекті емес және
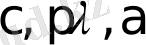 коэффициентері үздікті функциялар болып табылады (төртінші текті шартты шекаралық шартты көп қабатты жүйе. Әрбір қабатың ішінде
коэффициентері үздікті функциялар болып табылады (төртінші текті шартты шекаралық шартты көп қабатты жүйе. Әрбір қабатың ішінде
 () ізделінді функциясы жылуөткізгіштік теңдеуін өзінің коэффициенттерімен ал қабаттардың шекарасында түйіндесу шарттарын қанағаттандырады. )
() ізделінді функциясы жылуөткізгіштік теңдеуін өзінің коэффициенттерімен ал қабаттардың шекарасында түйіндесу шарттарын қанағаттандырады. )
Қарапайым жағдайда - қабаттар арасында идеал контакт болғанда, түйіндесу шарты температураның үздіксіздігімен жылу ағынының үздіксіздігіне негізделеді:
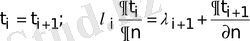
Қалың қабаттардан басқа нақты (реал) денелерде қабаттар арасындағы жылу берілу контактлік жылу алмасу арқылы іске асады (сәуле шығарудың, жылуөткізгіштіктің, конвекцияның күрделі процестері) . Контактлік жылу алмасуда шекаралық шартттарда дәл бере алмаймыз және есептеулер үшін жуық шешімдерді қолданады.
Жоғарғы энергиялы физиканың дамуымен бірге төртінші шекаралық шартты есептер жанама мәнге ие болды - олар ракета басының көпқабатты жамылғысы, энергия түрлендіргіштер және т. б.
д) Сызықты шекті есептерден басқа, шекаралық шарттары сызықты емес есептер де қарастырылады. Шекарада сәулелену заңы орындалатын, сәулелену арқылы жылу берілу есептері осыған жатады:
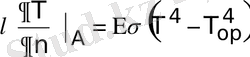
Мұндағы Е - беттің сәулелік қабілетін сипаттайтын қараю дәрежесі;
 - Стефан-Больцман тұрақтысы; Т
ор
-зерттейтін объектіні қоршаған орта мен дененің температурасы.
- Стефан-Больцман тұрақтысы; Т
ор
-зерттейтін объектіні қоршаған орта мен дененің температурасы.
4 текті шекаралық шартта есептерді сыртқы сызықтық емес есептері деп атаймыз. Сәулелену арқылы жылутасымалдану жоғары температураларда жұмыс істейтін барлық жүйелерге тән, сондықтан сыртқы сызықты емес есептер көкейісті болып табылады. Әйткенмен қазіргі уақытта бұл шекаралық шартты есептердің шешілгендерінің саны шектеулі, ал шешімнің ортақ әдістемесі жоқ.
ә) Айырым схемалары теориясының негізгі ұғымдарыӘртүрлі техникалық құрылғыларда өтіп жатқан жылуалмасу процестерінің неғұрлым толық моделдері қатты дененің және сұйықтық температуралары, жылу ағындары, сәулелену интенсивтілігі және т. б. сияқты ізделінді шамалардың біртекті емес кеңістік уақыттың өрістерін ескереді. Мұндай модельдер дербес туындылары бар дифференциалдық теңдеулер, интегралдық және теңдеулердің жүйесі болып келеді. Әйткенмен, нақты техникалық есептерді шешкенде, ережеге сай тек мұндай модельдерді қолданумен ғана шектеліп қалмайды, бұл бірнеше себептермен түсіндіріледі.
Біріншіден көптеген техникалық құрылғылар үшін толық математикалық модельдерді іске асыру құрылғылардың күрделі құрылымына және олардың құрамына енетін элементердің көп болуы себепті заманауи ЭЕМ -дарды қолданғанның өзінде қиындық туғызады. Пайда болған қиыншылықтар шешу тәсілін таңдауға және машиналық моделге енетін бастапқы ақпараттық көлеміне байланысты. Мұндай жүйелердің жылулық режимін талдау үшін барлық жүйені және оның әртүрлі бөліктерін ыждаһаттылықтың әртүрлі деңгейімен сипатталатын толық моделмен салыстырғанда неғұрлым қарапайымдарды тізбектеп қолдануға бағытталған кезең деп модельдеу [5] әдісі қолданылады.
Екіншіден, күрделі жүйелерді жобалаудың негізгі тәсілі жобалау процесінде жүйе деталдаудың біртіндеп өсетін дәрежесімен ирархияның әртүрлі деңгейлерінде тізбектеп қарастырылады. Бұл жағдайда қандай да бір жоғарғы деңгейдегі жылуалмасу процестерін талдауды, осы деңгейдің ішкі жүйелерінің ішкі құрылымы нақ егжей-тегжейлі анықталмаған жағдайда ғана жүргізе аламыз, сондықтан толық модельді ақпараттың жеткіліксіздігімен қолдана алмаймыз.
Соңында, көптеген техникалық есептерді шешу ізделінді шамалардың кеңістіктік таралуы жөнінде толық ақпаратты қажет етеді, бұл толық модельге ықшамдаулар енгізуді және қызықтыратын сұрақтарға тез арада және арзан жауап беруге мүмкіндік береді.
Бұл жылу алмасу процестерінің интегралдық сипаттамаларын есептеуге мүмкіндік беретін және алгебралық немесе әдеттегі дифференциалдық теңдеулермен сипатталатын ықшамдалған модельдерді қарастырудың көкейкесті екендігін көрсетеді. Бұдан ары мұндай модельдерді физикалық шамалардың кеңістік таралуын ескеретін, таралған параметрлі моделдерден бөлектеп, жинақталған (сосредоточенный) параметрлі модельдер деп атаймыз.
Практика жинақталған параметрлі моделдерді іске асырғанда осы түрдің жеткілікті ортақ моделін бөліп алып және олардың әрқайсысы үшін нақты есептердің кең ауқымын шешетін әмбебап программалық жасауға болатындығын көрсетеді. Бұл бөлімде өзара жылу алмасуға қатысатын жылутасымалдаушылар ағыны мен денелер жүйесіндегі орташа температураны есептеуге мүмкіндік беретін осындай модельдердің біреуі үшін программалау реализация мен сандық есептеу тәсілінің бірі шекті айырымдық схема (конечно-разностная схема) әдісін қарастырамыз. Баяндалатын тәсілдер мен әдістер жинақталған параметрлері басқа моделдер үшін де тура.
Орташа температураны есептейтін моделдері сипаттауға көшеміз. Бұл моделде үш түрлі объект қарастырылады: Қуатты Р
і
болатын жылу көздері бар бітекті Т
і
 температуралық өрістері бар қатты денелердің N
tk
көлемі; каналдың кірісінде
температуралық өрістері бар қатты денелердің N
tk
көлемі; каналдың кірісінде
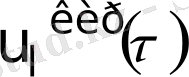 және каналдың шығысында
және каналдың шығысында
 орташа массалық температураға және
орташа массалық температураға және
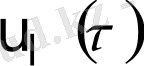 орташа массалық температураға ие жылу тасымалдағыштар енетін каналдардың N
k
көлем ;
орташа массалық температураға ие жылу тасымалдағыштар енетін каналдардың N
k
көлем ;
 тұрақты температураға ие орталардың N
ор
көлемінен тұрады.
тұрақты температураға ие орталардың N
ор
көлемінен тұрады.
1 сурет
Қатты денелер бір -бірімен, сонымен бірге жылу тасымалдағыштармен және ортамен жылу алмасады. Бұл моделде q алынған денеге i денеге P ik kg көрші денелер және P il жт жылу тасымалдағыштан және P il ор -ортадан келетін жылу ағындарын олардың орташа темеператураларының айырымы ретінде келесідей өрнектеуге болады:
 P
il
kg
P
il
kg

мұндағы
 i және j қатты дененің, і дене мен
i және j қатты дененің, і дене мен
 жылутасымалдағыш және і дене мен к орта арасындағы жылу өткізгіштік. Жылу өткізгіштіктерді жылу берілу және өлшем коэффициентеріне негіздеп есептейді. Олар жылу тасымалданудың әрқилы механизмдерін ескереді.
жылутасымалдағыш және і дене мен к орта арасындағы жылу өткізгіштік. Жылу өткізгіштіктерді жылу берілу және өлшем коэффициентеріне негіздеп есептейді. Олар жылу тасымалданудың әрқилы механизмдерін ескереді.
і денесінде бөлінетін Р і қуат оны жылытуға және қоршаған денелерге, жылутасымалдағыштарға және орталарға берілетіндіктен, жылу балансы теңдеуі келесідей жазылады.
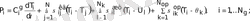 (26)
(26)
Мұндағы С
i
g
- дененің толық жылу сыйымдылығы
 көлемде жылутасымалдағышқа денелерден келетін жылу ағыны оның осы көлемдегі жылынуына шығындалады, сонымен бірге көлемнен ағып шығып жатқан жылутасымалдағышпен бірге кетеді. Сондықтан жылутасымалдағыш үшін жылу балансы теңдеуі
көлемде жылутасымалдағышқа денелерден келетін жылу ағыны оның осы көлемдегі жылынуына шығындалады, сонымен бірге көлемнен ағып шығып жатқан жылутасымалдағышпен бірге кетеді. Сондықтан жылутасымалдағыш үшін жылу балансы теңдеуі
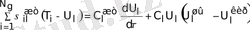
мұндағы
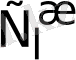 -
-
 көлемдегі жылутасымалдағыштың толық жылусыйымдылығы;
көлемдегі жылутасымалдағыштың толық жылусыйымдылығы;
 - меншікті жылусыйымдылық;
- меншікті жылусыйымдылық;
 -
-
 көлем арқылы өтетін жылутасымалдағыштың массалық шығыны.
көлем арқылы өтетін жылутасымалдағыштың массалық шығыны.
Моделде
 -ші каналдың кірісінде бірі басқа каналдан (m индексті),
-ші каналдың кірісінде бірі басқа каналдан (m индексті),
келесілері
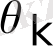 белгілі температураға ие көлемдерден (к индексті) келетін бірнеше ағындардың арасы жүреді деп есептелінеді. Сонда
белгілі температураға ие көлемдерден (к индексті) келетін бірнеше ағындардың арасы жүреді деп есептелінеді. Сонда
 -ші канал кірісіндегі жылу тасымалдағыштың орташа шығындық
-ші канал кірісіндегі жылу тасымалдағыштың орташа шығындық
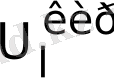 температурасы үшін келесі қатынас тура
температурасы үшін келесі қатынас тура
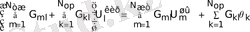 (27)
(27)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz