Бернулли теңдеуінің қолданылу аясын анықтау

Пән: Физика
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 32 бет
Таңдаулыға:

Мазмұны

Кіріспе . . .

: І.

Кіріспе. . .: Бөлім.

: 1. 1.

Кіріспе. . .: Идеал сұйықтың қозғалысы . . .

3: 4

: 1. 2.

Кіріспе. . .: Ағынның сызықтары мен түтіктері . . .

3: 6

: 1. 3.

Кіріспе. . .: Ағып жатқан сұйықтағы қысымды өлшеу . . .

3: 15

: 1. 4.

Кіріспе. . .: Сұйық қозғалысына импульстің сақталу заңын қолдану . . .

3: 17

: ІІ.

Кіріспе. . .: Бөлім.

: 2. 1.

Кіріспе. . .: Бернулли теңдеуі . . .

3: 20

: 2. 2.

Кіріспе. . .: Бернулли теңдеуін тәжірибеде қолдану . . .

3: 28

Кіріспе. . .:

Кіріспе. . .: Қорытынды . . .

3: 30

Кіріспе. . .: Пайдаланылған әдебиеттер . . .

3: 31

Кіріспе

Гидродинамика−механиканың сұйықтың қозғалысын зерттейтін бөлімі. Гидродинамикада - сұйық қозғалысының жалпы заңдары зерттеледі.

Сұйықтар сонау Архимед заманынан бері, яғни бұдан 2200 жыл бұрын зерттеле бастағанымен, гидродинамика әлі де қолданбалы ғылымның ең қиын саласының бірі болып табылады. Сұйықтардың қозғалыс теңдеулері белгілі бола тұрса да, бұл теңдеулерді есептеулер жүргізуге қолдану тым күрделі. Сұйықтардың қозғалысын қарастырудың өзі бірқатар әрі маңызды, әрі ғажайып қорытындылар жасауға мүмкіндік береді.

Курстық жұмыстың мақсаты $\mathbf{-}$ техника мен өндірістің негізі болған гидродинамика заңдарын пайдаланып, Бернулли теңдеуінің қолданылу аясын анықтау.

Гидродинамика сұйықтың қозғалысын, сол сияқты су асты қайығының, су көліктерінің қозғалысын зерттейді. Гидродинамика ілімін құруда швейцар физигі Д. Бернуллидің (1700-1782) еңбегі шексіз.

Сығылмайтын және қабаттарының арасындағы үйкелісті ескермеуге болатын сұйықты идел сұйық деп атайды. Сығылмайтын идеал сұйықтың механикалық энергиясының сақталу заңы Бернулли теңдеуімен беріледі. Бернулли теңдеуінің қолданыс табатын облысы соншалықты кең. Бернулли теңдеуін алу үшін ағысты стационар және ламинарлық, сұйықты сығылмайтын, ал тұтқырлықты ескерімсіз аз деп алады.

Гидродинамикада сұйықтардың құбырлар мен каналдар ішіндегі қозғалысын қарастырады және сұйықтардың әртүрлі денелерді (механикалық араластыру, қатты денелердің сұйықта тұнуы, т. б. ) толқындап ағуының заңдылықтарын қарастырады.

Идеал сұйықтың қозғалысы

Қатты денелердегі сияқты сұйықтар мен газдардың қозғалысын да кинематикалық және динамикалық тұрғыдан қарастыруға болады. Газдар мен сұйықтар өзара ұқсас болғандықтан оларды әдетте бірінен -бірін бөлмей, тек газдардың сығылғыштығын ескермеуге болмайтын жерде ғана олар бөлек қарастырылады. Сондықтан сұйық туралы айтылғандар газға да қатысты деп түсіну керек.

Кинематикалық тұрғыдан қарағанда сұйық қозғалысын оның әрбір бөлшегінің қозғалысымен сипаттауға болады. Сұйық қозғалысын жете түсіну үшін ағын сызықтары және ағын түтігі деген жаңа ұғымдарды пайдалану тиімді. Қалыптаспаған қозғалыс (стационар емес) үшін ағын сызықтары уақытқа байланысты өзгереді, ал қалыптасқан (стационар) жағдайда олар тұрақты болып қалады. Бұған қоса, қалыптасқан қозғалыс жағдайында ағын сызықтары бөлшектің траекториясына дәл келеді. [2, 38-бет]

Біз бұған дейін денелердің бір-бірімен салыстырғанда орын ауыстыруы немесе қатты денелердің бір белгілі осьтен айналуы болып табылатын қозғалыстарды қарастырдық. Алайда, бір дененің әр түрлі бөліктерінің бір-бірімен салыстырғанда орын ауыстыруы болып табылатын қозғалыстың да болуы мүмкін; бұл жағдайда, егер дене үздіксіз және шексіз үлкен деп қарастыруға жарайтын болса, оны тұтас орта деп атайды. Тұтас орта дегеніміз серпімді қатты дене болып келуі мүмкін, бұл жағдайда оның бір бөліктері екінші бөліктерімен салыстырғанда ығысуы және тербелуі (толқын пайда болуы) мүмкін; тұтас орта дегеніміз ағыс пайда бола алатын сығылмайтын сұйық болып келуі де мүмкін; ақырында тұтас орта дегеніміз ағыс та тербеліс те пайда бола алатын сығылатын сұйық немесе газ болып келуі мүмкін. Механиканың сұйықтың қозғалысын зерттейтін бөлімі гидродинамика деп аталады.

Сұйық қозғалысын қарастырғанда көп жағдайда, едәуір жуықтап, сұйықты мүлде сығылмайды деп санауға болады және оның бір қабаты екінші қабатымен салыстырғанда орын ауыстырғанда үйкеліс күштері (ішкі үйкеліс немесе тұтқырлық) пайда болмайды деп жоруға болады. Осындай мүлде сығылмайтын және мүлде тұтқыр емес сұйық идеал сұйық деп аталады. «Идеал сұйық» ұғымын пайдалану нақтылы сұйықтарға тек белгілі дәрежеде жақындау ғана болып табылады. [7, 149-бет]

Әр алуан сұйық қозғалысын екі түрге бөліп қарастыруға болады. Кейбір жағдайларда сұйықтың жеке қабаттары бір-біріне қатысты сырғанай отырып, араласпай ағады. Сұйықтың мұндай қозғалысы ламинарлық ағыс ( lamina -"қабат" деген латын сөзінен) деп аталады. Мысалы, жай ағатын өзендердегі судың ағысы ламинарлық ағысқа жатады. Ағынның жылдамдығы артқанда, ағыс сипаты өзгереді. Сұйықтың әр түрлі қабаттарының араласуы нәтижесінде құйындар түзіле ағатын қозғалысы турбуленттік ағыс ( turbulentus-" құйынды" дегенлатын сөзінен) деп аталады. Турбуленттік ағысқа, мысалы, өзендегі су құйындарының, мұхиттық ағыстардың, дауылдардың пайда болуын және т. б, жатқызуға болады.

Біз сұйық қабаттарының арасында үйкеліс болмайтын және тіпті сұйық сығылмайтын арнайы жағдайдағы сұйықтың ағысын қарастырамыз. Сұйық ағысы тұнық, турбулентті болмауы тиіс.

Сығылғыштығын және қабаттарының арасындағы үйкелісті ескермеуге болатын сұйықты идеал сұйық деп атайды. Реал сұйықтың қозғалыс динамикасы өте күрделі. Оны сипаттауды ықшамдау үшін кейбір жағдайларда ішкі үйкеліс күштерін ескермейміз. Мұндай сұйықты идеал сұйық дейміз. Идеал сұйықтың қозғалысы кезінде механикалық энергияның ішкі энергияға айналуы болмайды, яғни сұйықтың механикалық энергиясы сақталады. Сығылмайтын идеал сұйықтың механикалық энергиясының сақталу заңы Бернулли теңдеуімен беріледі. [6, 76-бет]

Ағынның сызықтары мен түтіктері

Сұйық бөлшектерінің қозғалысын бір белгілі санау системасына қатысты анықтайтын болайық. Сонда әрбір бөлшектің өзіне лайық жылдамдық векторы болады. Барлық сұйық, қалыптасқан сөзбен айтқанда, жылдамдық векторының өрісі болып табылады. Жылдамдық векторының өрісімен сызықтар жүргізейік, сонда олардың әрбір нүктесінен жүргізілген жанамалар сұйық бөлшегі жылдамдығының сол нүктедегі бағытына дәл келетін болсын (1. 1-сурет) . Сондай сызықтарды ағын сызықтары деп атайды.

$C:\Users\hp\Desktop\ЛЯЗКО\1.jpg$

1. 1-сурет. Сұйық ағынының сызықтары.

Әдетте ағын сызықтары былай жүргізіледі: сұйықтың ағысы күшті болғанда ағын сызықтарын тығыз етіп, сұйық ағысы бәсең жерде ағын сызықтарын сирек етіп жүргізеді. Сұйық ағысы қалыптасқан (стационар) жағдайда әрбір нүктедегі сұйық жылдамдығы тұрақты болады, уақытқа байланысты өзгермейді. Бұл жағдайда ағын сызықтары да өзгермейді және сұйықтың жеке бөлшектерінің траекториясына дәл келеді. Сұйықтың ағын сызықтарын көзге көрінетін етуге

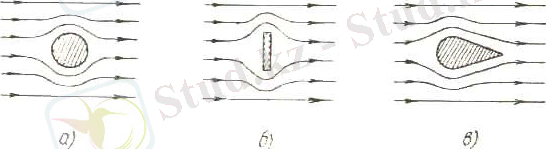
$C:\Users\hp\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\15.jpg$

1. 2-сурет. Сұйық ағынының сызықтары.

болады: ол үшін сұйыққа сорғалата ағызып бояу қосады немесе оған көрініп жүзіп жүретін бір зат бөлшектерін араластырады. 1. 2 а, б, в-суреттерде ағынға перпендикуляр қойылған дөңгелек цилиндрді, пластинканы және қимасы балық тәрізді сүйір денені сұйық орай аққан жағдайдағы ағын сызықтары көрсетілген.

Сұйықтың ағын сызықтарымен шектелген бөлігін ағын түтігі деп атайды. Ағын түтігінің белгілі қимасындағы барлық бөлшектер қозғалыс кезінде ағын түтігінің ішімен қозғалып отырады, одан шығып кетпейді. Сонымен қатар ағын түтігінің ішіне де сырттан ешқандай бөлшектер енбейді. Бір ағын түтігін алып, оның кез келген ∆S ₁ және ∆S ₂ нормаль қимасын сайлап алайық. (1. 3-сурет) .

$C:\Users\hp\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\17.jpg$

1. 3-сурет. Сұйық ағынының түтігі.

Уақыт бірлігі ішінде ∆S ₁ қимасынан ағып өтетін сұйық көлемі ∆S ₁ ϑ ₁ көбейтіндісіне тең болады, мұндағы ϑ ₁ мына ∆S ₁ қимасы алынған орындағы сұйық ағысының жылдамдығы. Уақыт бірлігі ішінде ∆S ₂ қимасынан ағып өтетін сұйық көлемі ∆S ₂ ϑ ₂ болады, мұндағы ϑ ₂ - осы ∆S ₂ қимасы алынған орындағы сұйық ағысының жылдамдығы. Сұйық сығылмайтын болғанда ∆S ₁ қимасынан ағып өтетін сұйық көлемі қандай болса, ∆S ₂ қимасынан ағып өтетін сұйық көлемді де дәл сондай болады, сондықтан:

∆S ₁ ϑ ₁ =∆S ₂ ϑ ₂

Бұл теңдік ағын түтігінің кез келген екі қимасы үшін дұрыс болады, сондықтан ағын түтігі үшін жалпы мынаны жазуға болады:

∆S∙ϑ=const,

яғни сығылмайтын, тұтқыр емес сұйық ағысының жылдамдығы мен ағын түтігінің көлденең қимасының көбейтіндісі берілген ағын түтігі үшін тұрақты шама болады. Бұл қатыс сорғыныңүзіліссіздігі жөніндегітеорема деп аталатын белгілі теорема.

Сығылмайтын, тұтқыр емес сұйықтың бір нағыз трубамен ағуы стационарлы ағын болса, сонда ол трубаның ішкі көлемі ағын түтігіне дәл келеді. Сондықтан сорғының үзіліссіздігі жөніндегі теорема бойынша трубаның жуан жерінде сұйық жайлап ағады, ал трубаның жіңішке жерінде сұйық тезірек ағады.

Бір ағын түтігін алайық, ол ағыс бағыты бойынша жіңішкере беретін болсын: ағын түтігінің таралу (жіңішке) жеріне келген сайын сұйық жылдамырақ аға бастайды, яғни үдеу пайда болады. Сондықтан, түтіктің тарлау жеріне ағып барған сұйыққа әлі сол түтіктің кең (жуан) жерінде тұрған сұйық тарапынан бір күш әсер етеді. Сұйық көлемінің ішінде пайда болатын ондай күш тек сұйықтың әр түрлі бөліктерінлегі қысымдар айырмасының есебінен ғана пайда бола алады. Күш түтіктің жіңішке жағына қарай бағытталғандықтан, түтіктің жуан жеріндегі қысым, оның жіңішке жеріндегі қысымнан артық болады. Ағын түтігі тарылған жерде қысым бәсең болады.

Ескерте кетейік, қысым (p) деп бір ауданға перпендикуляр бағытта әсер еткен F күшінің сол ∆S ауданына қатынасымен өлшенетін шаманы айтады.

Сұйық ағынынан оның белгілі бір ∆m массасын бөліп алайық, ол алдымен

ағын түтігінің ∆S ₁ қимасынан, кейін ∆S ₂ қимасынан ағып өтетін болсын(1. 4-сурет) . ∆S ₁ қимасы алынған жердегі сұйық жылдамдығын ϑ ₁ әрпімен, қысымды p ₁ әрпімен белгілеп, ал ∆S ₂ қимасы алынған жердегі жылдамдықты ϑ ₂ әрпімен, қысымды p ₂ әрпімен белгілейік. Ағын түтігі горизонталь орналаспай біраз көлбей орналасқан болсын; ∆S ₁ қимасы алынған орынның биіктігін h ₁ әрпімен, ∆S ₂ қимасы алынған орынның биіктігін h ₂ әрпімен белгілейік. Сұйықтың ∆m массасы ағып өткенде бірсыпыра жұмыс істелінеді, өйткені, сұйық ішінде p қысымы болған себепті, сұйықтың осы массасында белгілі күш әсер етеді.

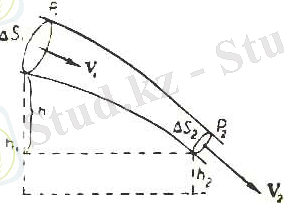
$C:\Users\hp\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\14.jpg$

1. 4-сурет. Сұйық ағынының түтігі

Мысалы, ∆S ₁ қимасынан ағып өтетін сұйықтың ∆m массасының толық энергиясы Е ₁ болсын, ал ∆S ₂ қимасынан ағып өтетін сұйықтың толық энергиясы Е ₂ болсын. Энергияның сақталу заңы бойынша энергияның Е ₂ -Е ₁ өзгерісі, ∆m массасын ∆S ₁ қимасынан ∆S ₂ қимасына дейіни қозғалтып баратын сыртқы күштердің жұмысына тең болады:

Е ₂ -Е ₁ =A (1. 1)

Ал Е ₁ және Е ₂ энергиялары сұйықтың ∆m массасының кинетикалық және потенциалдық энергияларынан құралады:

Е ₁ $= \frac{\mathrm{\Delta}m \bullet {\vartheta_{1}}^{2}}{2}$ +∆m∙gh ₁ ; E ₂ = $\frac{\mathrm{\Delta}m \bullet {\vartheta_{2}}^{2}}{2}$ +∆m∙gh ₂

Мынаған көз жеткізу де қиын емес: А жұмысы ∆S ₁ және ∆S ₂ қималары арасындағы барлық сұйық участогы қозғалғанда ∆t уақыты ішінде істелетін жұмысқа дәлме-дәл келеді, сонда осы ∆t уақыт ішінде әлгі қималардан сұйықтың ∆m массасы ағып өтеді. ∆m массасын бірінші қима тұрған орыннан өткізу үшін сұйық ϑ ₁ ∆t=∆ l ₁ кесіндісіне, ал оны екінші қима тұрған орыннан өткізу үшін ϑ ₂ ∆t=∆ l ₂ кесіндісіне жылжуы керек. Бөліп алынған сұйық участогының екі шетінің әрқайсысына түсетін күштер өз ретінше мынаған тең: F ₁ =p ₁ ∆S ₁ және F ₂ =−p ₂ ∆S ₂ . Бірінші күш-оң шама, өйткені ол сұйық ағысына қарай бағытталған; екінші күш-теріс шама, өйткені бұл күш қарастырылып отырған сұйық участогына қиманың оң жағында жатқан сұйық тарапынан әсер ететін

күш болып табылады, сондықтан ол сұйық ағысына қарама-қарсы жаққа қарай бағытталған болады. Ақырында мынадай теңдік шығады:

А=F ₁ ∆ l ₁ +F ₂ l ₂ =p ₁ ∆S ₁ ϑ ₁ ∆t-p ₂ ∆S ₂ ϑ ₂ ∆t

Енді Е ₁ , Е _2, А шамаларының осы табылған мәндерін (1. 1) теңдіктегі орындарына қойсақ, мынаны табамыз:

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\mathrm{\Delta}m \bullet {\vartheta_{2}}^{2}}{2}$ +∆m∙gh ₂ − $\frac{\mathrm{\Delta}m{\vartheta_{1}}^{2}}{2}$ −∆m∙gh ₁ =p ₁ ∆S ₁ ϑ ₁ ∆t−p ₂ ∆S ₂ ϑ ₂ ∆t

немесе

$\frac{\Delta m \bullet {\vartheta_{1}}^{2}}{2}$ +∆m∙gh ₁ + p ₁ ∆S ₁ ϑ ₁ ∆t= $\frac{\Delta m \bullet {\vartheta_{2}}^{2}}{2}$ +∆m∙gh ₂ +p ₂ ∆S ₂ ϑ ₂ ∆t (1. 2)

Сорғының үзіліссіздігі жөніндегі заң бойынша сұйықтың ∆m массасының көлемі тұрақты болып отырады:

∆V=∆S ₁ ϑ ₁ ∆t=∆S ₂ ϑ ₂ ∆t

Енді (1. 2) теңдіктің оң жағын да, сол жағын да осы ∆V көлеміне бөлеміз және $\frac{\Delta m}{\Delta V}$ қатынасы сұйықтың тығыздығы ρ екендігін еске аламыз, сонда мына теңдік шығады:

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\rho{\vartheta_{1}}^{2}}{2}$ ρgh ₁ +p ₁ = $\frac{\rho{\vartheta_{2}}^{2}}{2}$ +ρgh ₂ +p ₂ (1. 3)

Бұл теңдеуді ең алғаш аса көрнекті физик және математик, Петербург академигі Даниил Бернулли (1700-1782) . Россияда істеп жүрген жылдары қорытып шығарған. Мұны Бернулли теңдеуі деп атайды.

Ағын түтігі горизонталь (h ₁ =h ₂ ) болып орналасқан жағдайда Бернулли теңдеуі мына түрде жазылады:

$\frac{\rho{\vartheta_{1}}^{2}}{2}$ +p ₁ = $\frac{\rho{\vartheta_{2}}^{2}}{2}$ +p ₂ (1. 3a)

(1. 3а) формула мен сорғының үзіліссіздігі жөніндегі теоремаға қарағанда, сұйық қимасы әр түрлі горизонталь трубамен аққан кезде, труба жіңішкерген жерде сұйық жылдамдығы зор болады, ал ол кеңейген жерде қысым зор болады. Осы айтылғанды трубаның бойына a, b, c манометр түтіктерін орнатып, тәжірибе жасап көруге болады (1. 5-сурет) .

$C:\Users\hp\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\18.jpg$

1. 5-сурет. Қысымның түтіктің диаметріне тәуелділігі.

Сондай түтіктер ішіндегі сұйық деңгейінің биіктігі трубадағы p қысымын көрсетеді. Осылай тәжірибе жасағанда, Бернуллидің заңына лайық, трубаның жіңішке жеріне орнатылған b манометр түтігіндегі сұйықтың деңгейі, оның кеңейген жеріне орнатылған манометр түтіктеріндегі сұйық деңгейлерінен төмен екендігі байқалады.

Енді сұйық ағынының ішіне жылжымайтын манометр түтігін орнатайық, оның төменгі имек ұшы ағынға қарсы қойылсын (1. 6-сурет, «Пито түтігі»), сонда осы түтіктің маңайындағы ағын сызықтары өзгереді. Түтік тесігінің алдындағы

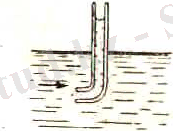
$C:\Users\hp\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\19.jpg$

1. 6-сурет. «Пито түтігі»

сұйықтың жылдамдығы нольге тең болады. Осы айтылған мысалға (1. 3а) формуланы қолдансақ және ϑ ₂ =0 деп ұйғарсақ, сонда

p ₂ =p ₁ + $\frac{\rho{\vartheta_{1}}^{2}}{2}$

Манометр түтігінің тесігін ағынға қарсы қойғанда өлшенетін p ₂ қысымы p ₁ қысымынан $\frac{\rho{\vartheta_{1}}^{2}}{2}$ шамасындай артық болады. (Ағынмен бірге қозғалған манометр p ₁ қысымын көрсеткен болар еді) . Егер p ₁ қысымы мәлім болса, p ₂ қысымын өлшеп тауып, ағынның ϑ ₁ жылдамдығын есептеп шығаруға болады. $\frac{\rho{\vartheta_{1}}^{2}}{2}$ шамасын кейде «динамикалық қысым» деп атайды.

Ағыс жылдамдығы үлкен болған кезде трубаның жіңішке жеріндегі p қысым теріс шама болуы мүмкін. Бұл жағдайда трубаның жіңішке жерлерінен ағып өтетін сұйық тұс-тұсынан сығылады. Егер трубаның жуан жерінде қысым атмосфералық қысымға тең болса, ал трубаның жіңішке жерінде ол атмосфералық қысымнан кем болады. Сонда сорғы ағын сорып алу әсерін тигізетін болады. Бірсыпыра приборлардың, мысалы, пульверизатордың және су сорғалама насосының, жұмыс істеуі тарылған сорғының сорып алу әсеріне негізделген. Су сорғалама насосының схемасы 1. 7-суретте көрсетілген. Түтіктің тарылған А ұшынан үлкен жылдамдықпен ағып шыққан су ауаның көпіршіктерін сорып алады да, оларды өзімен бірге қоса ағызып әкетеді

$C:\Users\hp\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\110.jpg$

1. 7-сурет. Су сорғалама насосы

Бернулли теңдеуін пайдаланып сұйықтың тесіктен ағып шығу жылдамдығын табуға болады. Егер ыдыстың өзі кең, тесігі кішкене болса (1. 8-сурет), онда ыдыстағы сұйықтың жылдамдығы аз болады да, барлық ағынды бір ағын түтігі

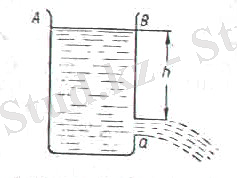
$C:\Users\hp\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\Л6.jpg$

1. 8-сурет. Бүйірдегі тесіктен сорғы ағынның ағып шығуы

ретінде қарастыруға болады. Қысым жоғарғы қимада да (сұйықтың АВ бетінде), төменгі қимада да (а тесігінде) атмосфералық $P_{0}$ қысымға тең. Сондықтан (1. 3) Бернулли теңдеуі мына түрде жазылады:

$\frac{{\vartheta_{1}}^{2}}{2}$ +g(h ₁ -h ₂ ) = $\frac{{\vartheta_{2}}^{2}}{2}$ (1. 3б)

Егер ыдыстағы сұйық жылдамдығы ϑ ₁ =0 болып келгендегі сұйықтың тесіктен сорғалап ағуын қарастырсақ және h ₁ -h ₂ =h деп алсақ (1. 8-сурет), онда

ϑ ₂ = $\sqrt{2gh}$ ,

яғни сұйықтың сорғы ағынының һ биіктіктен сорғалап аққанда алатын жылдамдығы, дене сол биіктіктен еркін түскенде алатын жылдамдыққа тең болады. [7, 149-154 бет]

Ағып жатқан сұйықтағы қысымды өлшеу

Сұйықтағы қысым оның ағыс жылдамдығының шамасына байланысты екені мәлім. Қысымды өлшеу үшін сұйыққа енгізілген прибор сұйықтың қозғалу сипатын бұзады, демек, өлшенетін қысымның шамасын да өзгертуге болады. Ұшындағы тесігі ағынға қарай бағытталған имек манометрлік түтікті сұйық ішіне орналастырайық (1. 9-сурет) . Мұндай түтікті Пито түтігі деп атайды. Ұшы түтік тесігінің центріне тірелетін ағын сызығын қарастырдық. Қарастырылып отырған ағын сызығының өн бойындағы жылдамдық түтіктен едәуір алыс қашықтықтағы ұйтқымаған ағын үшін ϑ шамасынан бастап тесіктің дәл алдындағы

$C:\Users\hp\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\Л.JPG$

1. 9-сурет 1. 10-сурет

нольге тең өзгереді. Бернулли теңдеуі бойынша тесік алдындағы (сондай-ақ, манометрлік түтіктегі) қысым ұйтқымаған ағындағы p қысымнан $\frac{\rho\vartheta}{2}^{2}$ шамасына артық болады. Демек, Пито түтігімен жалғасқан манометр

pʹ=p+ $\frac{{\rho\vartheta}^{2}}{2}$ (1. 4)

шамасына тең қысымды көрсетеді.

Қысыммен өлшемдес $\frac{{\rho\vartheta}^{2}}{2}$ қосылғышты динамикалық қысым деп аталады. p қысымын статикалық қысым деп атау келісілген. Статикалық және динамикалық қысымның қосындысына тең pʹ қысымы толық қысым деп аталады. Сонымен Пито түтігі арқылы (1. 4) теңдеуіндегі толық қысымды өлшеуге болады.

Егер имек жіңішке түтіктің бүйірінен тесіктер жасалса, онда мұндай тесіктер маңындағы жылдамдық (сондай-ақ, қысым) ұйтқымаған ағындағы жылдамдықпен (қысыммен де) шамалас болады (1. 10-сурет) . Сондықтан зонд деп аталатын мұндай түтікке қосылған манометр, сұйықтағы p статикалық қысымды көрсетеді.

Толық және статикалық қысымды біле отырып, $\frac{{\rho\vartheta}^{2}}{2}$ динамикалық қысымды, демек, ϑ ағын жылдамдығын (сұйықтың тығыздығы белгілі деп саналады) табуға болады. Егер Пито түтігі мен зондты 1. 11-суретте көрсетілгендей етіп біріктіріп, оны дифференциалдасақ манометрдің (яғни қысымның айырмасын өлшейтін манометрдің) әр түрлі тармағына қоссақ,

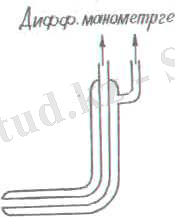
$C:\Users\hp\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\Л5.jpg$

1. 11-сурет

онда манометр тікелей динамикалық қысымды көрсетеді. Манометрді ϑ жылдамдықтың мәндері бойынша градуирлеп, сұйықтың ағыс жылдамдығын өлшейтін приборды алуға болады. [3, 206-208 бет]

Сұйық қозғалысына импульстың сақталу заңын қолдану

Басқа денелер тәрізді сұйық пен газға да импульстың сақталу заңы қолданылады. Бұл заңды кейбір есептерді шешуге пайдаланайық.

Ағып жатқан сұйықтың имек трубаның қабырғасына түсіретін реакциясы. Имек трубада сығылмайтын сұйықтың стационар ағыны орнығып болды деп жориық (1. 12-сурет) . Есепті жеңілдету үшін S қимасы тұрақты труба алайық. Онда сорғының үздіксіздігі нәтижесінде әрбір қимадағы жылдамдық шама жағынан бірдей және ϑ-ге тең болады.

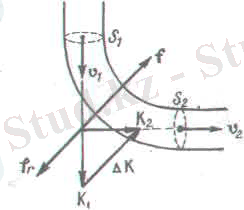
$C:\Users\hp\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\Л4.jpg$

1. 12-сурет

Трубаның S ₁ және S ₂ қималарымен шектелген имек учаскесінің көлемін қарастырайық. ∆t уақыт ішінде S ₁ қимасы арқылы бұл көлемге импульсы K=ρSϑV ₁ ∆t шамасына тең Sϑ∆t сұйық мөлшері ағып келеді. Бір мезгілде S ₂ қимасы арқылы осы көлемнен мөлшері дәл сондай, импульсы K=ρSϑV ₂ ∆t шамасындай сұйық ағып өтеді. Сонымен, трубаның имек учаскесінің ∆K=K ₂ −K ₁ =ρSϑ(V ₂ -V ₁ ) ∆t шамасындай импульс өсімшесін береді. Уақыт бірлігі ішіндегі импульс өсімшесі әсер етуші күшке тең екендігін білеміз. Демек, труба қабырғалары сұйыққа тең әсерлі F= $\frac{\mathrm{\Delta}K}{\mathrm{\Delta}t}$ =ρSϑ(V ₂ −V ₁ ) күшпен әсер етеді. Ньютонның үшінші заңы бойынша ағып жатқан сұйық труба қабырғасына

${\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ F}_{r}$ =ρSϑ(V ₁ −V ₂ ) (1. 5)