Қатты денелер кинематикасы: гироскоптық күштер және прецессия


Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 37 бет
Таңдаулыға:
ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
ТАРАЗ МЕМЛЕКТТІК ПЕДАГОГИКАЛЫҚ ИНСТИТУТЫ
КАФЕДРА
ТАҚЫРЫБЫ:
КУРС:
ТОП:
ОРЫНДАҒАН:
ҚАБЫЛДАҒАН:
ҚОРҒАУҒА ЖІБЕРІЛДІ:
ҚОРҒАҒАН БАҒАСЫ:
ТАРАЗ-2013ж.
Кіріспе
I. Қатты дене кинематикасы . . .
1. 1. Қатты дененің ілгерілмелі қозғалысы . . .
1. 2. Қатты дененің тұрақты осьті айнала қозғалысы . . .
1. 3. Есеп . . .
1. 4. Қатты дененің жазық параллель қозғалысы . . .
1. 5. Еркін қатты дене қозғалысы . . .
II. Гироскоптар . . .
2. 1. Гироскоптық күштер . . .
2. 2. Гироскоп прецессиясы . . .
Қорытынды . . .
Пайдаланылған әдебиеттер . . .
Кіріспе
Мен осы курстық жұмысымда теориялық механиканың кинематика бөліміне тоқталдым.
Теориялық механика - материялық денелердің механикалық қозғалысының жалпы заңдылықтары, мен тепе - теңдігін және осы материялық денелердің өзара механикалық әсерлесуін зерттейтін ғылым. Өзара механикалық әсерлесу нәтижесінде бір материялық денелер басқа материялық денеге қарағанда қозғалысқа келтіріледі, яғни материялық денелер өзінің бастапқы қалпын өзгертеді (деформацияланады) немесе жоғарыда аталған екі жағдай қатар байқалады.
Осы курстық жұмыстың негізгі мақсаты - қазіргі кезеңде отандық машина жасау өндірісін дамыту, жаңа өндірістік технологияларды халық шаруашылығына енгізу, космос кеңістігін игеру және тағы басқа техникалық шешімдерді анықтауды қажет ететін күрделі мәселелер механика ғылымының қарыштап дамуына өзінің ықпалын тигізетіні сөзсіз.
Теориялық механика пәні статика, кинематика және динамика деп аталатын үш бөлімнен тұрады.
Статика теориялық механиканың күштер (күштер жүйесі) түуралы ілім баяндалатын және осы күштер әсер еткендегі материялық денелердің салыстырмалы тепе - теңдік шарттары мен теңдеулері зерттелетін бөлім.
Егер дене басқа денелермен салыстырғанда тыныштық күйде болса, онда дене тепе - теңдікте болады деп айтуға болады. Дененің тепе - теңдік шарты дененің күйіне байланысты. Сұйық және газ тәрізді денелердің тепе - теңдігі гидростатика және аэростатика пәндерінде қарастырылады.
Кинематика деп материялық денелер озғалысының геометриялық сипаттамаларын (траекториясын, үдеуін, жылдамдығын), зерттйтін теориялық механика тарауын айтады. Осы зерттеулерде денелердің инерттілігі (массасы) және оларға әсер ететін күштер есепке алынбайды. Сондықтан да кинематиканы қозғалыс геометриясы деп те кейде оны «төрт өлшемді гещметрия» деп те, атайды. Өйткені Ньютон механикасында, яғни қазіргі кезеңдегі теориялық механиканың негізі болып саналатын классикалық механика да, материя (материялық дене) орын ауыстыратын кеңістіктің қасиеттері үш өлшемді эвклидтік кеңістіктің аксиомалары мен теоремаларына тәуелді болады да, ал төртінші өлшем ретінде дәл кеңістік сияқты материяға тәуелсіз, абсолютті шама - уақыт алынады.
Динамика бөлімінде материялық нүктенің, қатты дененің қозғалысы зерттелгенде, осы қозғалыстың себебі болатын әсер етуші күштер және материялық обьектілердің инерттілігі (масса) ескеріледі.
Осы курстық жұмыс арқылы теориялық механиканың әр түрлі өнеркәсіптердің негізі бола алатын ғылым ретінде таныдым.
1. Қатты денелер кинематикасы
Материялық нүктелердiң кез келген жинағын материялық система деп атайды.
Әрбiр нүктесiнiң кеңiстiктегi орны және қозғалысы оның басқа нүктелерiнiң орындары мен қозғалыстарына тәуелдi болатын материялық системаны механикалық система деп атайды.
Абсолют қатты дене механикалық системаның кез келген екi нүктесiнiң арақашықтығы өзгермейтiн жеке түрi болып табылады ол кейде өзгермейтiн механикалық система деп аталады.
Кеңiстiкте кез келген бағытта қандай болмасын жылдамдықпен орын ауыстыра алатын системаны еркiн система деп атайды.
Еркiндiгi белгiлi бiр шарттармен шектелген системаны еркiн емес система деп, ал оның еркiндiгiн шектеп тұрган шарттарды байланыстар деп атайды.
Механикалық системаларды құраушы нүктелердiң қозғалыстарының тәуелдiлiгi нүктелердiң өзара әсерiнен және байланыстардың әсерiнен туады.
Нүктелердiң система iшiнде өзара орналасуын шектейтiн шарттар (система нүктелерiнiң өзара әсерi) iшкі байланыстар деп, тұтас системаға түсiрiлген байланыстар сыртққы байланыстар деп аталады. Тек қана iшкi байланыстары бар система еркін система болады.
Байланыстар бiр теңдеулермен (кейде теңсiздiктермен) өрнектеледi. Бұл теңдеулердiң түрiне қарай байланыстар екi топқа бөлiнедi.
Егер байланыс системаның, демек, оны құрайтын барлық нүктелердiң, кез келген уақыт кезеңiндегi кеңiстiктегi орнын ғана шектейтiн болса, яғни оны өрнектейтiн теңдеуге тек система нүктелерiнiң координаталары ғана қанағаттандыратын болса, ондай байланыс геометриялык немесе шектi байланыс деп аталады.
Система n нүктеден тұрады десек, оған түсiрлген геометриялық байланыстың теңдеуi жалпы былай жазылады:
f (
 х, у, z; t ) = 0 (1. 1)
х, у, z; t ) = 0 (1. 1)
Системаның кеңiстiктегi орнымен қатар жылдамдығын да шектейтiн байланыстарды кинематикалық немесе дифференциалдық байланыстар дейдi. Оларды өрнектейтiн теңдеулердiң құрамына система нүктелерiнiң кез келген уақыт кезеңiндегi координаталары және олардың уақыт бойынша алынған бiрiншi туындылары да кiредi:
φ (
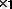 х
1
, …,
х
1
, …,
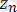
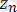 ;
;
 х
2
, …,
х
2
, …,
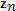
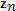 ; t ) =0. (1. 2)
; t ) =0. (1. 2)
Тек қана геометриялық байланыстар әсер ететін системалар голономдық системалар деп, геометриялық байланыстармен қатар кинематикалық байланыстары да бар системалар голономдық емес системалар деп аталады. Осыған орай кейде геометриялық байланыстарды голономдық, ал интегралданбайтын дифференциалдық байланыстарды голономдық емес байланыстар деп атайды. (1. 2)
Бiз бұдан былай тек голономдық системалар қозғалысын ғана оқып үйренемiз. Голономдық емес системалар кездесетiн жағдайлар ерекше ескертiледi.
Еркiн емес системаның кеңістiктегi орнын бiр мәндi анықтайтын тәуелсiз координаталардың саны оны құрайтын барлық нүктелердiң координаталарының санынан кем болады. Шынында да, n нүктеден тұратын голономдық системаға r геометриялық байланыстар (1. 1) түсірілсiн. Сонда системаның кеңістiктегi орнын, яғни конфигурациясын анықтайтын 3n координаталардың (Зn-k) -сы ғана тәуелсiз болады, өйткенi қалғандары бұлар арқылы берiлген k байланыстың теңдеулерiнен анықталады. Бұл тәуелсiз координаталар система координатал ары (немесе системаның жалпыланған координаталары) деп аталады және оның кеңiстiктегi орнын бiр мәндi анықтайды. Система координаталарының жиыны оның конфигурациясы делiнедi. Система конфигурациясын өлшемдерiнiң саны система координаталарының санына тең кеңiстiкте қаралып отырған бiр нүктелің координаталары деп қарауға болады. Бұл нүктенi системаның өрнектеушi нүктесi деймiз.
Еркiн нүктенiң кез келген уақыт кезеңiндегi таңдап алынған координаталар системасына қарагандағы кеңiстiктегi орны өзара тәуелсiз үш скалярлық координаталарымен анықталады. Таңдап алынған координаталар системасының түріне қарай олар сызықтық та, бұрыштық та шамалар болуы мүмкiн. Олар жалпыланған (қисық сызықты) координаталар деп аталып, әдетте
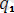
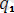 (t),
(t),
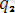
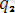 (t),
(t),
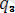
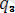 (t) арқылы белгiленедi.
(t) арқылы белгiленедi.
Іс жүзiнде байланыс белгiлi бiр бет немесе қисық ретiнде берiледi. Олардың теңдеулерi нүктенiң қозғалысын шектейтiн шарттар болып табылады. Мысалы, материялық нүкте радиусы R сфераның iшiнде және iшкi бетiнде ғана қозғала алатын болса, онда байланыс былай өрнектеледi:
х²+y²+z²≤R²
Егер нүкте барлық уақытта белгiлi бiр қисықтың, не беттiң үстiнде қозғалуға тиiс болса, онда нүктенiң координаталары сол қисықтың, не беттің теңдеулерiне қанағаттандыруға тиiс, яғни қозғалушы нүктенiң координаталары соңғылардың ағым координаталары болуға тиіс.
Өзiнiң түрiн өзгертпейтiн, яғни деформацияланбайтын, кеңістікте қозғалмайтын, уақытқа тәуелсiз байланыстар станционар (тұрақты) немесе склероном байланыстар деп, ал уақыт өткен сайын өзiнiң түрiн немесе кеңiстiктегi орнын өзгертiп тұратын байланыстар, мысалы (1. 2) стационар емес (айнымалы) немесе реоном байланыстар деп аталады. Стационар байланыстардың теңдеулерiне уақыт кiрмейдi.
Системаға (нүктеге) әсерi еш уақытта тоқтамайтын, яғни әсерiнен қозғаушы система құтыла алмайтын байланыстар құтқармайтын немесе екi жақты байланыстар деп аталады. Олар (1. 1), сияқты теңдiктермен өрнектеледi. Қозғалыстағы системаға (нүктенің әсері белгiлi бiр уақыт кезеңiнде тоқтайтын байланыстар құтқаратын (босататын) немесе бiр жақты байланыстар делiнедi. Мысалы, байланыс бетінен, не қисығынан нүкте бiр жағына қарай түсе алады. Бұл жағдайда байланыс тек кеңiстiктiң материялық нүкте шыға алмайтын бөлiгiн шектеп тұрады және теңсiздiктермен өрнектеледi.
Еркiн емес нүктелердiң жалпыланған координаталарының саны үштен кем болады. Мысалы, нүкте берiлген қисықтың бойымен қозғалуға мәжбүр болса, оның кез келген уақыт кезеңiндегi кеңiстiктегi орнын анықтауға нүктенiң бір ғана доғалық координатасы s=s(t) жеткiліктi. Шынында да, жалпыланған координаталардың бiрiнің, мысалы
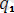
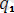 -нiң, орнына доғалық координатаны қабылдасақ қалган екеуi сол арқылы берiлген қисықтың (траекторияның) - байланыстың координаталық екi теңдеунен
-нiң, орнына доғалық координатаны қабылдасақ қалган екеуi сол арқылы берiлген қисықтың (траекторияның) - байланыстың координаталық екi теңдеунен
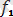
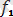 (s,
(s,
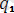 q
1
,
q
1
,
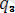
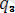 ) =О, (i=1, 2) анықталады. Әрине, нүктенi системаның және түрі деп қарауға болады. Берiлген қисықтың теңдеулерi геометриялық байланыстар екенi сөзсiз. Олай болса берiлген траекторияның бойымен қозғалушы нүкте бір нүктеден тұратын голономдық система екен.
) =О, (i=1, 2) анықталады. Әрине, нүктенi системаның және түрі деп қарауға болады. Берiлген қисықтың теңдеулерi геометриялық байланыстар екенi сөзсiз. Олай болса берiлген траекторияның бойымен қозғалушы нүкте бір нүктеден тұратын голономдық система екен.
Голономдык системаның (нүктенiң) кез келген уақыт кезеңiндегi кеңiстiктегi орнын бір мәндi анықтайтын өзара тәуелсiз скалярлық функциялардың (системаның жалпыланған немесе қисық сызықты координаталарының, ал қысқаша система координаталарының) санын системаның (нүктенiң) еркiндiк дәреже саны деп атайды.
Аргументтерi уақъгг болып келетiн сол скалярлық функциялардың өздерi системаның қозғалыс теңдеулерi немесе қозғалыс заңы деп аталады.
Система кинематикасының негiзгi мақсаты қозғалушы системаның еркiндiк көрсеткiшiнiң санын анықтау, оның жалпыланған координаталарының дұрыс тағайындап, таңдап алынған координаталар системасындағы қозғалыс теңдеулерiн мүмкiндiгiнше ең қарапайым түрде жазу болып табылады. Қозғалыстың басқа кинематикалық характеристикаларын, қасиеттерiн анықтау математикалық жолмен жүргiзiледi.
Еркiн абсолют қатты дененің еркiндiк дәреже санын және қозғалыс теңдеулерiн анықтайық.
Ол үшiн берiлген А денесiнiң (1. 1-сурет) таңдап алынған Оζηξ декарттық координаталар системасымен салыстырғандағы орнын бір мәндi анықтайтын өзара тәуелсiз координаталарды табу керек. Қатты дененiң кеңiстiктегi орны оның бiр түзудің бойында жатпайтын кез келген үш нүктесiнiң координаталарымен бiр мәндi анықталады, осындай үш нүктеде, мысалы Мi (
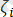
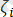 ,
,
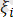
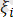 ,
,
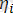
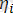 ), (i=1, 2, 3) нүктелерiнде, бекiтiлтен А денесi қозғалмайды.
), (i=1, 2, 3) нүктелерiнде, бекiтiлтен А денесi қозғалмайды.
Үш нүктенiң тоғыз координатасы бар, бiрақ дене абсолют қатты болғандықтан олар өзара төмендегiдей үш шартпен байланысқан:
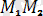
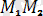 =соnst=
=соnst=
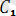
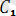 ,
,
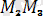
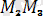 =соnst=
=соnst=
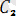
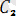 ,
,
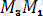
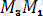 =соnst=
=соnst=
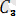
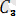 .
.
Демек, тоғыз координатаның тек алтауы ғана өзара тәуелсiз болады, яғни еркiн қатты дененiң еркiндiк дареже саны алтыға тең. Тағы да қосымша нүктелер қарасақ еркiндiк дәреже саны арта ма? Жок, артпайды. Себебi жаңадан қанша координата қосылса оларды байланыстыратын сонша теңдеулер де қосылады. Мысалы, қосымша
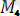
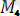 нүктесін қарасақ, оның үш координатасымен бiрге оны алдыңғы үш нүктемен қосатын кесiндiлердiң ұзындыктарының тұрақтылығын өрнектейтiн үш шарт та қосылады.
нүктесін қарасақ, оның үш координатасымен бiрге оны алдыңғы үш нүктемен қосатын кесiндiлердiң ұзындыктарының тұрақтылығын өрнектейтiн үш шарт та қосылады.
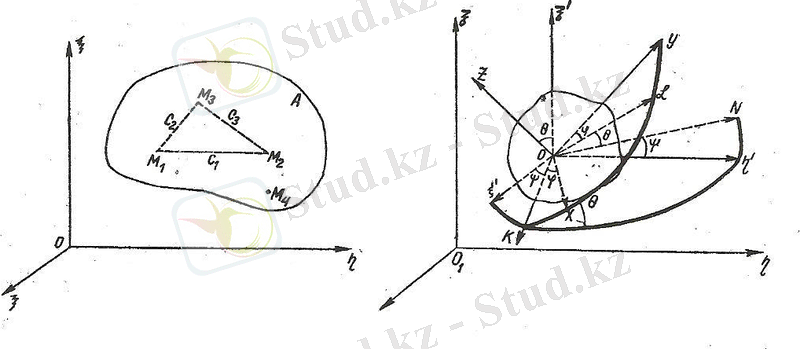
1. 1-сурет 1. 2-сурет
Сонымен, көрсетілген тоғыз координатаның кез келген алтауы белгілі болса, қалған үшеуі жоғарыдағы теңдеулерден анықтап, деннің кеңістіктегі орнын дәл көрсете аламыз.
Бұл қорытындыға басқаша да жолмен келуге болады. Қозғалмайтын
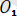
 , ζ η ξ координаталар системасынан басқа денемен бірге бекітілген қозғалмалы Охуz декарттық координаталар системасын (1. 2-сурет) таңдап алалық. Қозғалмайтын және қозғалмалы координаталар осьтерінің бірлік векторларын әруақытта да сәйкес l, m, n және i, j, k деп белгілеуге келіселік.
, ζ η ξ координаталар системасынан басқа денемен бірге бекітілген қозғалмалы Охуz декарттық координаталар системасын (1. 2-сурет) таңдап алалық. Қозғалмайтын және қозғалмалы координаталар осьтерінің бірлік векторларын әруақытта да сәйкес l, m, n және i, j, k деп белгілеуге келіселік.
Жылжымалы Охуz координаталар системасы денемен бiрге қозғалып жүретiндiктен оның
 ζηξ системасымен салыстығандағы жағдайын бiлу дененiң кеңiстiктегi орнын бiлумен бiрдей. Абсолют қатты дененiң қозғалысын кинематикалық зерттеу сол денемен өзгерместей болып бекiтiлген қозғалмалы кеңiстiктiң (Охуz координаталар системасының) қозғалмайтын кеңiстiктегi
ζηξ системасымен салыстығандағы жағдайын бiлу дененiң кеңiстiктегi орнын бiлумен бiрдей. Абсолют қатты дененiң қозғалысын кинематикалық зерттеу сол денемен өзгерместей болып бекiтiлген қозғалмалы кеңiстiктiң (Охуz координаталар системасының) қозғалмайтын кеңiстiктегi
 ζηξ координаталар системасындағы) қозғалысын зерттеуге келтiрiледi.
ζηξ координаталар системасындағы) қозғалысын зерттеуге келтiрiледi.
Қозғалмалы және қозғалмайтын кеңiстiктердiң атқаратын мiндеттерiн алмастыруға, яғни қатты дене (Охуz системасы) тыныштықта тұрады, ал кеңiстiк (
 ζηξ системасы) қозғалыста болады деп қарауға болады. Бұл жағдайда қозғалыстың кинематикалық характеристикалары өзгермейдi.
ζηξ системасы) қозғалыста болады деп қарауға болады. Бұл жағдайда қозғалыстың кинематикалық характеристикалары өзгермейдi.
Бұл ақиқат қозғалыстың қайтымдылық принципi деп аталады. Ал Охуz системасының
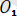 ζηξ системасымен салыстырандағы жағдайы оның О (ζ˳ (η˳ ξ˳) нүктесiнің ‚үш координатасымен және қозғалмалы осьтердiң (i, ј=1, 2, 3) тоғыз бағыттаушы косинусымен анықталады. Бiрақ,
ζηξ системасымен салыстырандағы жағдайы оның О (ζ˳ (η˳ ξ˳) нүктесiнің ‚үш координатасымен және қозғалмалы осьтердiң (i, ј=1, 2, 3) тоғыз бағыттаушы косинусымен анықталады. Бiрақ,
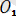 O
1
(ζηξ) және Охуz координаталар системалары тiк бұрышты болғандықтан
O
1
(ζηξ) және Охуz координаталар системалары тiк бұрышты болғандықтан
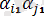
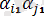 +
+
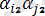
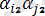 +
+
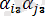
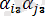 =
=
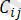
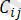 (1. 3) болады.
(1. 3) болады.
Мұнда i=ј болғанда,
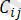
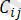 =1, ал і ≠ ј болғанда,
=1, ал і ≠ ј болғанда,
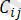
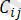 =0 болады.
=0 болады.
Демек, тоғыз бағыттаушы косинустың үшеуi ғана өзара тәуелсiз де, қалғандары жоғарыдағы теңдiктерден солар арқылы анықталады. Сонымен, дененiң кеңiстiктегi орнын бiр мәндi анықтау үшiн О нүктесiнiң
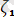
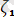 ,
,
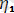
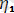 ,
,
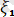
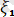 үш координатасын (сызықтық шамаларды) және қозғалмалы осьтердiң кез келген үш бағытттаушы косинусын (бұрьштық шамаларды) бiлсек жеткiлiктi, яғни еркiн қатты дененiң алты еркiндiк ережесi бар.
үш координатасын (сызықтық шамаларды) және қозғалмалы осьтердiң кез келген үш бағытттаушы косинусын (бұрьштық шамаларды) бiлсек жеткiлiктi, яғни еркiн қатты дененiң алты еркiндiк ережесi бар.
Бұл қаралған ең жалпы жағдай болғандықтан қандай да болмасын қозғалыстары қатты дененiң еркiндiк дәреже саны алтыдан аспайды. Денеге түсiрiлген байланыстар оның еркiндiк дәрежелерiнiң, демек, қозғалыс теңдеулерiнiң, санын тек қана кемiтедi.
Механикада тәуелсiз үш бұрыштық шаманың орнына әдетте Эйлер бұрыштары деп аталатын φ, ψ және θ шамалары (1. 2) қабылданады. Эйлер бұрыштары Охуz системасының осьтерi
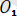
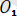 ζηξ системасының сәйкес осьтеріне параллель қосымша Оζ'η'ξ' системасымен салыстырғандағы жағдайын бiр мәндi анықтайды және жоғарыдагы тоғыз бағыттаушы косинусты Эйлер бұрыштары арқылы бiр мәндi өрнектеуге болады.
ζηξ системасының сәйкес осьтеріне параллель қосымша Оζ'η'ξ' системасымен салыстырғандағы жағдайын бiр мәндi анықтайды және жоғарыдагы тоғыз бағыттаушы косинусты Эйлер бұрыштары арқылы бiр мәндi өрнектеуге болады.
Эйлер бұрыштары көбіне астрономияда қабылданған терминдермен аталады.
Егер соңгы системада дененiң кез келген М нүктесiнің координаталарын
 x
1
,
x
1
,
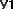 y
1
y
1
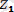 , z
1
десек, онда тiк бұрышты координаталар системасын белгiлi бiр бұрышқа бұру формулалары бойынша
, z
1
десек, онда тiк бұрышты координаталар системасын белгiлi бiр бұрышқа бұру формулалары бойынша
ζ'=
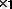 x
1
cos ψ -
x
1
cos ψ -
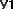 y
1
sin ψ, η' =
y
1
sin ψ, η' =
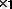 x
1
sin ψ +
x
1
sin ψ +
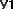 y
1
cos ψ, ξ'=
y
1
cos ψ, ξ'=
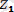
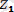
Егер М нүктесiнің
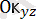
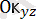 системасындағы координаталарын
системасындағы координаталарын
 x
2
,
x
2
,
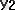 y
2
,
y
2
,
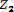 z
2
десек, онда екiншi бұрудың нәтижесiнде мынадай болады:
z
2
десек, онда екiншi бұрудың нәтижесiнде мынадай болады:
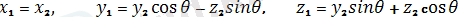
Үшiншi бұрудың нәтижесiнде алатынымыз:
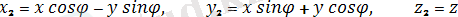
Аралық координаталарды тиiстi орындарына қойып, ықшамдағаннан кейiн былай жазуға болады:
ξ=
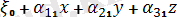
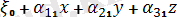 ,
,
η=
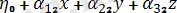
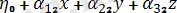 ,
,
ζ=
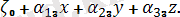
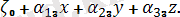
Мұнда
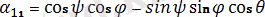
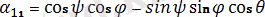
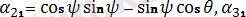
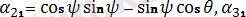 sin ψ sin θ,
sin ψ sin θ,
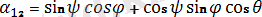
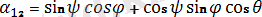
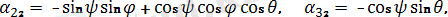
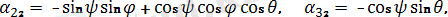
Бұл формулалар бағыттаушы косинустардың Эйлер бұрыштары арқылы өрнектелгендiгiн көрсетедi.
Сонымен, еркiн қатты дененiң мынадай алты қозғалыс теңдеуi болады:
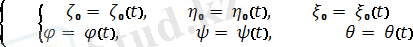
 (1. 4)
(1. 4)
Байланысқан қатты денелердiң еркiндiк дәрежелерiнің саны да, демек, қозғалыс теңдеулерiнiң саны да алтыдан кем болады. Мысалы, бiр ұшы (О нүктесi) ζОη жазықығында параллель жазықтықта жылжып жүретiн жiңiшке таяқшаның еркiндiк көрсеткiштерiнiң саны төртке тең. Шынында да ондай таяқшаның кеңiстiктегi орны (таяқшаның осiн жылжымалы осьтердiң бiреуiнiң, айталық Ох осiнiң, бойымен бағыталған деуге болады) О нүктесiнiң η
0
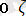 ζ жазықтығындағы координаталарымен (
ζ жазықтығындағы координаталарымен (
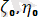
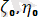 ) және Ох осінің кез келген екi бағыттаушы косинусымен, мысалы
) және Ох осінің кез келген екi бағыттаушы косинусымен, мысалы

 ( ал
( ал
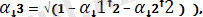
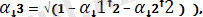 анықталады. Сонымен, бұл таяқшаның қозғалыс теңдеулерi мынадай болады:
анықталады. Сонымен, бұл таяқшаның қозғалыс теңдеулерi мынадай болады:


Қатты дене, қозғалысының негізгi екi түрi бар. Олар ілгерiлемелi және айналмалы қозғалыстар. Қатты дененiң қандай болмасын жеке алынған басқа қозғалысы осы екi қозғалыстың өз-өздерiмен немесе бір-бiрiмен қосындысы болып табылады.
Кейiн бұл қатты дене қозғалысының негiзгi түрлерiн, туғызушы себептердiң де табиағаты әр түрлi болатынын көремiз.
1. 1 Қатты дененiң iлгерiлемелi қозғалысы
Қатты дене қозғалысының денемен өзгерместей боп бекiтiлген кез келген түзу өзiне-өзi параллель бола отырып қозғалатын түрiн дененің iлгерiлемелi қозғалысы деп атайды.
Берiлген қатты дененiң (2. 3-сурет) iлгерiлемелi қозғалысын зерттеу үшін қозғалмайтын және денемен бiрге бекiтiлген Охуz қозғалмалы координаталар системаларын таңдап алалық. Әрине, қозғалмалы координаталар системаларын бас нүктесi О ретiнде қозғалушы екенiң кез келген нүктесiн, ал оның осьтерiн кез келген бағыттта алуға болатындыгы түсiнiктi. Бiрақ бiз зерттеудi жеңiлдету үшiн екi системаның сәйкес координаталар осьтерiн өзара параллель етiп алайық. Таңдап алынған бас нүктенiң қозғалмайтын системасымен салыстырғандағы кеңiстiктегi орны

 радиус-векторымен, ал дененiң кез келген М нүктесiнiң қозғалмалы Охуz системасымен салыстырғандағы орны r=OM радиус-векторымен анықталады. Дене абсолют қатт және тек қана iлгерiлемелi қозғалыста болғандықтан r радиус-векторы шамасы жағынан да бағыты жағынан да тұрақты болады. яғни оның координаталар осьтерiне проекциялары a, b, c тұрақты сандар болады. Суреттегi
радиус-векторымен, ал дененiң кез келген М нүктесiнiң қозғалмалы Охуz системасымен салыстырғандағы орны r=OM радиус-векторымен анықталады. Дене абсолют қатт және тек қана iлгерiлемелi қозғалыста болғандықтан r радиус-векторы шамасы жағынан да бағыты жағынан да тұрақты болады. яғни оның координаталар осьтерiне проекциялары a, b, c тұрақты сандар болады. Суреттегi
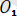
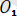 ОМ векторлық үшбұрышынан М нүктесiнің системасымен салыстырғандағы орны көрсетiлген радиус-векторлардың қосындысымен, яғни
ОМ векторлық үшбұрышынан М нүктесiнің системасымен салыстырғандағы орны көрсетiлген радиус-векторлардың қосындысымен, яғни
R =
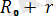
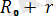 (1. 5) радиус-векторымен анықталатынын көреміз.
(1. 5) радиус-векторымен анықталатынын көреміз.
Мұнда r=соnst болағндықтан дененің кез келген М нүктесiнiң, демек, дененiң өзiнiң кеңiстiктегi орнын анықтауға О нүктесiнiң кез келген уақыт кезеңiндегi үш координатасын (ζ˳, η˳, ξ˳) бiлген жеткiлiктi. Сонымен, iлгерiлемелi қозғалыстағы қатты дененiң еркiндiк дәреже саны үшке тең. Ілгерiлемелі қозғалыстың (2. 5) векторлық теңдеуiн қозғалмайтын координаталар осьтерiне проекциялап, дененiң координаталық түрдегi қозғалыс теңдеулерiн былай жазуға болады:
ξ(t) =
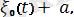
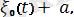
η(t) =
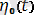
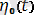 + b,
+ b,
ζ(t) =
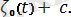
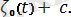
Бұл теңдеулер М нүктесi траекториясының параметрлiк теңдеулерi болады. Дененiң қозғалыс теңдеулерiнен М нүктесiнiң траекориясы О нүктесiнiң траекториясын r радиус-векторының оң бағытында өзiне-өзiн параллель көшiру арқылы алынатындығы анық байқалады. Сонымен, iлгерiлемелi қозғалыстағы қатты дененiң барлық нүктелерiнiң траекторияларын бiлу үшiн оның бір ғана мысалы, О нүктесiнiң траекториясын бiлген жеткiлiктi.
Әр түрлi уақыт кезеңдерiндегi сәйкес нүктелерiнiң арасын қосатын кесiндiлер, мысалы ОМ кесiндiсi өзара параллель және тең болатын мұндай қисықтар (траекториялар) эквидистанттық немесе конгруэнттi қисықтар (траекториялар) деп аталады. Iлгерiлемелi қозғалыстағы дене нүктелерiнiң траекториялары кез келген эквадистанттық қисық сызықтар болуы мумкiн.
Iлгерiлемелi қозғалыстары қатты дененiң барлық нүктелерiнiң өз траекториялары бойымен қозғалу заңдары бiрдей болады, өйткенi
dS =
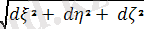
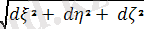 =
=
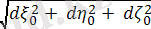
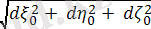 (1. 6)
(1. 6)
яғни олар тең уақыт аралықтарында тең жолдар өтедi.
Дененiң (1. 5) қозғалыс теңдеуiнің екi жағынан да уақыт бойынша туынды аламыз, сонда
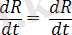
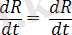
немесе

 (1. 7)
(1. 7)
яғни iлгерiлемелi қозғалыстағы қатты дененiң барлық нүктелерiнiң кез келген уақыт кезеңiндегi жылдамдықтары өзара тең болады. Тек iлгерiлемелi қозғалыс кезінде ғана тұтас дененiң жылдамдығы туралы сөз етуге болады және дененің жылдамдық векторы еркiн, яғни дененің қай нүктесiне де түсiруге болатын вектор болады.
Қатты дененiң iлгерiлемелi қозғалысын кейде кез келген уақыт кезеңiнде дененiң барлық нүктесiнiң жылдамдықтары өзара тең болатын қозғалыс деп те анықтайды. Мұндай қозғалысты перманенттiк (тұрақты) iлгерiлемелi қозғалыс деп атаймыз.
Егер (1. 7) теңдiк тек бір ғана уақыт кеаеңi үшiн орындалатын болса, қатты дене қозғалысының мұндай жағдайын лездiк iлгерiлемелi жылдамдықтар күйi деп атайды.
Денеде үдеу векторларының орналасуын анықтау үшiн (1. 7) теңдіктен уақыт бойынша туынды алайық:
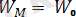
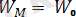 (1. 8)
(1. 8)
Яғни перманенттiк iлгерiлемелi қозғалыстағы қатты дененiң барлық нүктелерінің кез келген уақыт кезеңiндегi үдеулерi өзара тең. Лездiк ілгерiлемелi жылдамдықтар күйiндегi қатты дененiң барлық нүктелерiнің қаралып отырған уақыт кезеңіндегi үдеулерi де тең болады деуге болмайды. Өйткенi аргументтiң белгiлi бір мәнiнде өз мәндерi тең әр түрлi функциялардың сол нүктеде туындылары да тең деуге болмайды.
Сонымен, перманенттiк iлгерiлемелi қоғалыстағы қатты дененiң барлық нүктелерiнiң кез келген уақыт кезеңiндегi сәйкес кинематикалық характеристикалары бiрдей, яғни олардың бiреуiнiң ғана, мысалы О нүктесiнiң қозғалысын зерттеп бiлсек болғаны. Ал нүкте қозғалысын зерттеудi бiз бiлемiз. Ілгерiлемелi қозғалыстағы қатты дененiң жеке нүктелерiнiң қозғалысы ешқандай шектелмегендігiн айта кету қажет.
1. 2 Қатты дененiң тұрақты осьтi айнала қозғалысы
Денемен өзгермейтiндей боп бекiтiлген, айналу осi деп аталатын бір ғана түзудiң барлық нүктелерi тыныштық қалпын сақтайтын қозғалысты қатты дененiң сол тұрақты осьтi айнала қозғалысы дейдi.
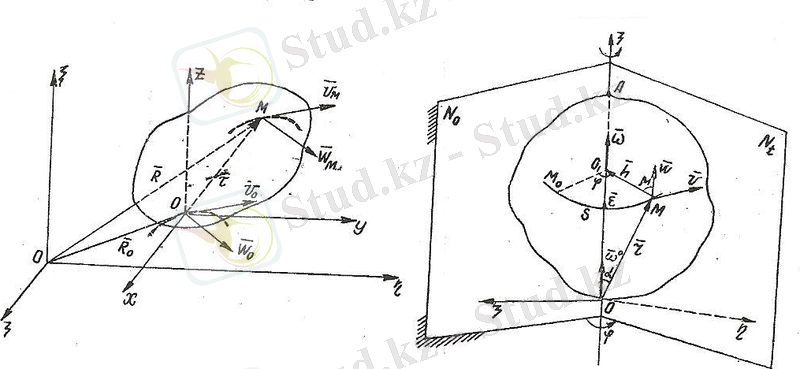
1. 3-сурет 1. 4-сурет
Берiлген дененiң (1. 4-сурет) қозғалмайтын 0А осiнен айнала қозғалысын зерттеу үшiн қозғалмайтын оң координаталар системасын таңдап алалық. Айналу осiн екi нүктеде, мысалы О және А нүктелерiнде, бекiтсек болғаны оның барлық нүктелерi де қозғалмайды. Тұрақты Оζ осiн осы тузудiң бойымен оның оң бағытынан қараған бақылаушы дене айналуын сағат тiлiнiң қозғалысына қарсы бағытта көретiндей етiп бағыттайық.
Сонда Оζ осi дененiң айналу осi болады. Жалпы жағдайда Оζ осiнiң айналу осiмен бiрiгiп келуi шарт емес. Тек бұл жағдайда зерттеу жеңiлденедi.
Айналу осi арқылы
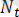
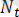 жазықтығын денемен бiрге бекiтейiк. Бастапқы кезеңде (t=0 болғанда) ол жазықтықты
жазықтығын денемен бiрге бекiтейiк. Бастапқы кезеңде (t=0 болғанда) ол жазықтықты
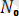
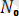 деп белгiлейiк және ол Оζ осi арқылы өтетiн болсын дейiк. Кез келген t уақыт өткен соң ол жазықтық денемен бiрге айнала отырып,
деп белгiлейiк және ол Оζ осi арқылы өтетiн болсын дейiк. Кез келген t уақыт өткен соң ол жазықтық денемен бiрге айнала отырып,
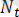
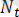 қалпына келедi.
қалпына келедi.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz