Функцияны интерполяциялау: теориясы және электрондық курс құру


Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 41 бет
Таңдаулыға:
ҚАЗАҚСТАН РЕСПУБЛИКАСЫ ҒЫЛЫМ ЖӘНЕ БІЛІМ МИНИСТРЛІГІ
МАТЕМАТИКА, ФИЗИКА ЖӘНЕ ТЕХНОЛОГИЯЛАР ФАКУЛЬТЕТІ
Математикалық үлгілеу және компьютерлік технологиялар құжырасы
КУРСТЫҚ ЖҰМЫС
тақырыбы «ФУНКЦИЯНЫ ИНТЕРПОЛЯЦИЯЛАУ» МАТЕРИАЛДАРЫ НЕГІЗІНДЕ ЭЛЕКТРОНДЫҚ КУРС ҚҰРУ
МАЗМҰНЫ
КІРІСПЕ
1 ФУНКЦИЯНЫ ИНТЕРПОЛЯЦИЯЛАУ
1. 1 Интерполяциялау есебінің қойылуы
1. 2 Әртүрлі ретті ақырғы айырмалар
1. 3 Айырмалар кестесі
1. 4 Жалпыланған дәреже
1. 5 Ньютонның интерполяциялық формулалары
1. 5. 1 Ньютонның бірінші интерполяциялық формуласы
1. 5. 2 Ньютонның екінші интерполяциялық формуласы
1. 5. 3 Функцияның кестесін тығыздау
1. 5. 4 Ньютонның интерполяциялық формуласының қалдық мүшелері
1. 6 Лагранж интерполяциялық формулалары
1. 6. 1 Лагранж интерполяциялық формуласы
1. 6. 2 Лагранж интерполяциялық формуласының ықшамдалған түрі
1. 6. 3 Лагранж формуласы бойынша есептеуді ұйымдастыру
1. 6. 4 Бірдей қашықтықта орналасқан түйіндер үшін Лагранж
интерполяциялық формуласы
1. 6. 5 Лагранж интерполяциялық формуласының қалдық мүшесін бағалау
1. 7 Гаусс интерполяциялық формулалары
1. 7. 1 Гаусстың бірінші және екінші интерполяциялық формулалары
1. 8 Стирлинг интерполяциялық формуласы
2 «ФУНКЦИЯНЫ ИНТЕРПОЛЯЦИЯЛАУ» ЭЛЕКТРОНДЫҚ КУРСЫН ҚҰРУ
2. 1 Электрондық курстың құрылымы
2. 2 HTML тілі және оның командаларын қолдану
2. 3 FrontPage бағдарламалық жабдығы
2. 4 «Функцияны интерполяциялау» курсының құрылымы
ҚОРЫТЫНДЫ
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ
КІРІСПЕ
Күнделікті өмірде кездесетін көптеген ғылыми-техникалық есептерді шешу барысында бір функцияны басқа бір функциямен жуықтатуға тура келеді. Мұндай есептер әсіресе эксперимент нәтижесінде алынған сандарды өңдеу мәселелерімен тығыз байланысты. Мысалы, функция алдын ала белгісіз болып, оның дискретті мәндері эксперимент арқылы алынған болса, онда осы мәндер арқылы функцияы жуықтатуға болады, не болмаса функцияның аналитикалық түрі өте күрделі болса, онда оны есептеу үшін қарапайым функциямен алмастырады.
Әдетте, жуықтаушы функцияны интерполяциялаушы функция деп атайды. Соңғы аталған функция көбінесе алгебралық полином болғандықтан, оны кейде итерполяциялаушы полином деп те атайды. Олар анықталған интегралдарды жуық шамамен есептеуде, дифференциалдық теңдеулердің шешімдерін табуда т. с. с. кеңінен қолданылады.
Курстық жұмыстың мақсаты: Ньютон, Лагранж, Гаустың бірінші және екінші интерполяциялық формулаларын, Стирлинг интерполяциялық формуласын қарастыру, «Функцияны интерполяциялау» электрондық курсын құру.
Жоғарыдағы интерполяциялау формулаларының қорытылу жолдарын қарастырып, аталған тақырыпқа электрондық курс құрып оларды методикалық нұсқаулар ретінде студенттерге ұсыну.
Курыстық жұмыстың өзектілігі: жұмыстың нәтижелерін «Сандық әдістер» пәнінен зертханалық сабақтарды жүргізу барысында, студенттердің өз бетімен жұмысын ұйымдастыруда, білім деңгейлерін толықтырып отыруда, емтиханға дайындалу үрдісінде көмек беретін, қашықтықтан оқыту кезінде қолдануға болады мемлекеттік тілде электрондық курс құру.
Курстық жұмыс теориялық, электрондық курс құру бөлімдерінен, кіріспеден, қорытындыдан, әдебиеттер тізімінен тұрады.
Теориялық бөлімінде «Функцияны интерполяциялау» формулаларына толықтай талдау жасалып, қортылу жолдарын қарастырамыз. Электрондық курс жасау бөлімінде HTML тілінің мүмкіншіліктеріне, Web - парақтардың элементтеріне, FrontPage бағдарламалық жабдығына шолу жасалып, «Функцияны интерполяциялау» электрондық курсының құрылымдық элементтеріне толығырақ тоқталамыз.
Курстық жұмыс нәтижелерін «Сандық әдістер» пәнінен информатика, қолданбалы математика, математика, ақпараттық жүйелер мамандықтары бойынша даярланатын студенттер үшін зертханалық сабақтарды жүргізу кезінде методикалық нұсқау ретінде қолдануға болады.
1 ФУНКЦИЯНЫ ИНТЕРПОЛЯЦИЯЛАУ
1. 1 Интерполяциялау есебінің қойылуы
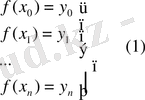 Бізге функция [a, b] аралығында кесте түрінде берілген. [a, b] аралығы тең
Бізге функция [a, b] аралығында кесте түрінде берілген. [a, b] аралығы тең
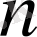 бөлікке бөлінген.
бөлікке бөлінген.
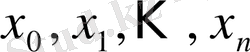 - интерполяциялау түйіндері деп аталады.
- интерполяциялау түйіндері деп аталады.
Белгілі бір класқа жататын, интерполяциялау түйіндерінде қабылдайтын мәндері,
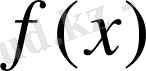 функциясының кестелік
функциясының кестелік
 мәндерімен бірдей болатын, яғни:
мәндерімен бірдей болатын, яғни:
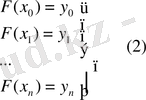
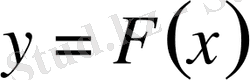 - функциясының түрін анықтау керек
.
- функциясының түрін анықтау керек
.
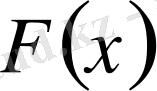 - интерполяциялаушы функция деп аталады. Геометриялық тұрғыдан қарастырсақ, графигі
- интерполяциялаушы функция деп аталады. Геометриялық тұрғыдан қарастырсақ, графигі
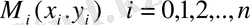 нүктелер жүйесі арқылы өтетін
нүктелер жүйесі арқылы өтетін
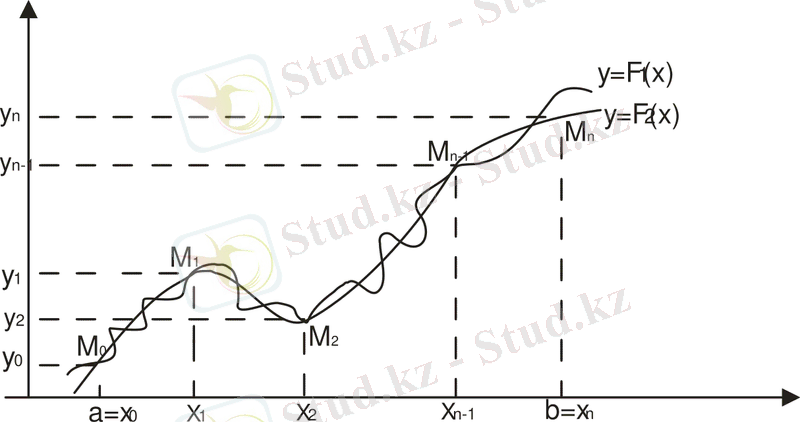
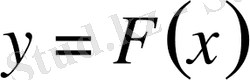 қисығын анықтау керек. Жалпы түрде қойылған мұндай есептің шешімі өте көп болады немесе жоқ болады (сурет 1. 1) .
қисығын анықтау керек. Жалпы түрде қойылған мұндай есептің шешімі өте көп болады немесе жоқ болады (сурет 1. 1) .
Егер
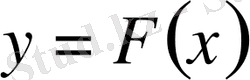 функциясын
функциясын
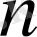 -ші дәрежелі полином түрінде іздесек, жоғарыда қойылған есеп бір мәнді шешіледі.
-ші дәрежелі полином түрінде іздесек, жоғарыда қойылған есеп бір мәнді шешіледі.
Сонымен функцияны интерполяциялау есебі төмендегідей түрде қойылады:
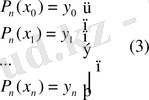 Дәрежесі
Дәрежесі
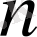 -нен артық емес, интерполяциялау түйіндерінде қабылдайтын мәндері
-нен артық емес, интерполяциялау түйіндерінде қабылдайтын мәндері
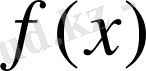 функциясының кестелік мәндерімен бірдей болатын, яғни:
функциясының кестелік мәндерімен бірдей болатын, яғни:
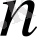 -ші дәрежелі
-ші дәрежелі
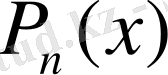 полиномының түрін анықтау қажет. Табылған полиномды
интерполяциялаушы функция
деп атайды.
полиномының түрін анықтау қажет. Табылған полиномды
интерполяциялаушы функция
деп атайды.
Сурет 1. 1
1. 2 Әртүрлі ретті ақырғы айырмалар
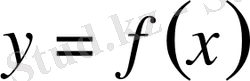 функциясы берілген.
функциясы берілген.
 арқылы функцияның аргументінің өсімшесін белгілейік (қадам) .
арқылы функцияның аргументінің өсімшесін белгілейік (қадам) .
Онда:
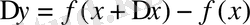
 функциясының бірінші ақырғы айырмасы деп аталады.
функциясының бірінші ақырғы айырмасы деп аталады.
Осы сияқты жоғарғы ретті ақырғы айрмаларын анықтауға болады:
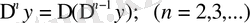
Мысалы:
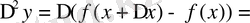
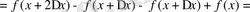
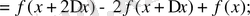
Мысал қарастырайық:
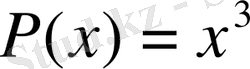 функциясы үшін ақырғы айырмаларын құрыңдар, қадам
функциясы үшін ақырғы айырмаларын құрыңдар, қадам
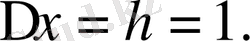
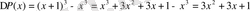

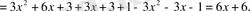
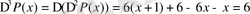
3-ші ретті ақырғы айырманың тұрақты екені көрініп тұр.
Егер
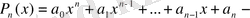
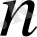 -ші ретті көпмүшелік болса, онда оның
-ші ретті көпмүшелік болса, онда оның
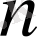 -ші ретті ақырғы айырмасы тұрақты, және
-ші ретті ақырғы айырмасы тұрақты, және
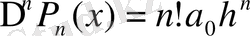 формуласымен анықталады. Мұндағы
формуласымен анықталады. Мұндағы

Шындығында да:
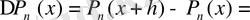
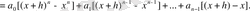
Ньютон биномының формуласын қолданып,
 -тің
-тің
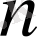 -1
-ші ретті полином екендігіне көз жеткіземіз:
-1
-ші ретті полином екендігіне көз жеткіземіз:
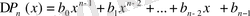 , мұндағы
, мұндағы
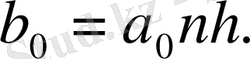
Дәл осындай жолмен
 -тің
-тің
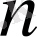 -2
-ші ретті полином болатындығын анықтаймыз:
-2
-ші ретті полином болатындығын анықтаймыз:
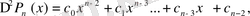 мұндағы
мұндағы
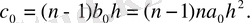
Осылайшы қарастыра отырып:
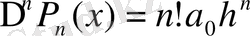 екендігіне көз жеткіземіз.
екендігіне көз жеткіземіз.
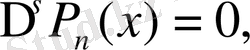 егер
егер

Мұндағы
 символын
символын
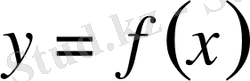 функциясына сәйкес
функциясына сәйкес
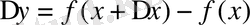 қоятындай оператор ретінде қарастыруға болады.
қоятындай оператор ретінде қарастыруға болады.
Мұндағы
 - тұрақты және
- тұрақты және
 үшін төмендегідей қасиеттер орынды болады:
үшін төмендегідей қасиеттер орынды болады:
1)
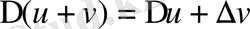
2)
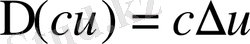 с
- тұрақты
с
- тұрақты
3)
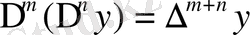 (оператор теоремасынан белгілі) .
(оператор теоремасынан белгілі) .
1. 3 Айырмалар кестесі
Практикада
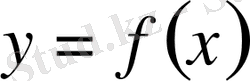 функциясы көбінесе кесте түрінде беріледі, яғни
функциясы көбінесе кесте түрінде беріледі, яғни
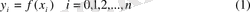
Мұндағы
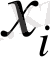 нүктелері бір-бірінен бірдей қашықтықта орналасқан, яғни қадам тұрақты:
нүктелері бір-бірінен бірдей қашықтықта орналасқан, яғни қадам тұрақты:
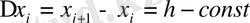 .
.
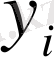 -ақырғы айырмаларды төмендегі қатынастардың көмегімен анықтауға болады:
-ақырғы айырмаларды төмендегі қатынастардың көмегімен анықтауға болады:
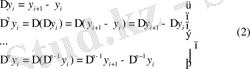
Сонымен
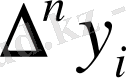 ақырғы айырмасын анықтау үшін
ақырғы айырмасын анықтау үшін
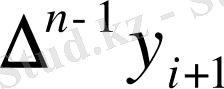 және
және
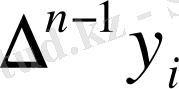 анықтау керек.
анықтау керек.
Алдымызға төмендегідей есеп қояйық:
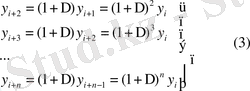
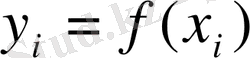 кестелік мәндерін ғана пайдаланып,
кестелік мәндерін ғана пайдаланып,
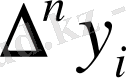 есептейтіндей формуланы қорытып шығаруға бола ма?
есептейтіндей формуланы қорытып шығаруға бола ма?
(2) -нің бірінші теңдеуінен:
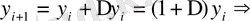
Ньютон биномының формуласын қолданып,
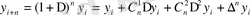 . Енді
. Енді
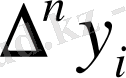 Ньтон биномының көмегімен жазайық:
Ньтон биномының көмегімен жазайық:
 .
.
Немесе
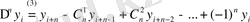 (4)
(4)
Мысалы:
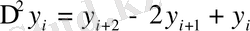
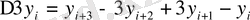 т. с. с.
т. с. с.
Сонымен
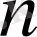 -ші ретті ақырғы айырманы есептеу үшін
-ші ретті ақырғы айырманы есептеу үшін
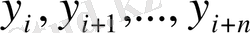 тізбегінің
тізбегінің
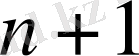 мүшесінің белгілі болуы жеткідікті.
мүшесінің белгілі болуы жеткідікті.
Ақырғы айрмаларды есептеу үшін горизонталь және диагоналдық кестелерді қолдануға болады.
Практикада көбінесе диагоналдық кестелер қолданылады:
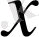
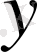

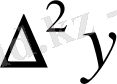

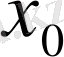
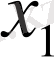
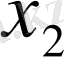
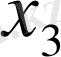


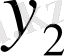
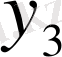
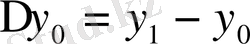
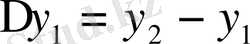
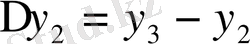


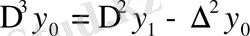
1. 4 Жалпыланған дәреже
Анықтама.
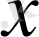 санының
санының
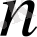 -ші дәрежесі деп бірінші мүшесі
-ші дәрежесі деп бірінші мүшесі
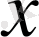 , ал әрбір келесі мүшесі алдыңғы мүшесінен
, ал әрбір келесі мүшесі алдыңғы мүшесінен
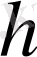 -қа кем болатын
-қа кем болатын
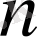 көбейткіштердің көбейтіндісін айтады, яғни:
көбейткіштердің көбейтіндісін айтады, яғни:
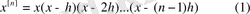
Мұндағы
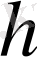 -кезкелген белгіленген тұрақты сан.
-кезкелген белгіленген тұрақты сан.
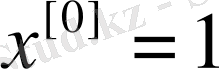 .
.
Ал
 болғанда, кәдімгі дәрежемен сәйкес келеді:
болғанда, кәдімгі дәрежемен сәйкес келеді:
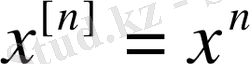 ,
,
 .
.
Жалпыланған дәреженің бірінші ақырғы айырмасын қарастырайық:


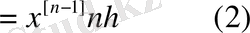
Сол сияқты:

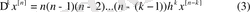
Мұндағы
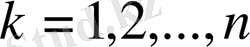 .
.
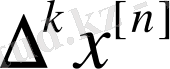 =0, егер
k>n
.
=0, егер
k>n
.
1. 5 Ньютонның интерполяциялық формулалары
1. 5. 1 Ньютонның бірінші интерполяциялық формуласы
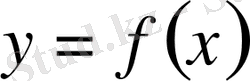 функциясы
функциясы
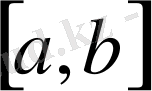 аралығында кесте түрінде берілген.
аралығында кесте түрінде берілген.
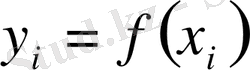
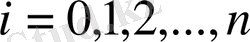 берілген болсын. Интерполяциялау түйіндері бір-бірінен бірдей қашықтықта орналасқан, яғни:
берілген болсын. Интерполяциялау түйіндері бір-бірінен бірдей қашықтықта орналасқан, яғни:

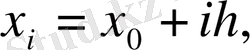
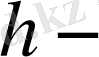 const.
const.
Интерполяциялаушы полиномды төмендегідей түрде іздейміз:
(1) полиномы төмендегідей екі шартты қанағаттандыруы қажет:
1) (1) -дің дәрежесі n -нен артық емес болу қажет.
2) (1) полиномының интерполяциялау түйіндерінде қабылдайтын мәндері кесте түрінде берілген
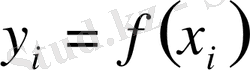 мәндерімен бірдей:
мәндерімен бірдей:
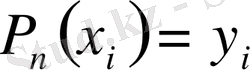 және
және
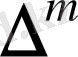
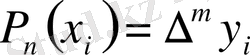 ,
,
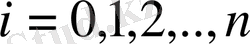
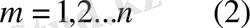
Жалпыланған дәреженің анықтамасын пайдаланып, (1) -ді төмендегідей түрде жазайық:
 .
.
Сонымен,
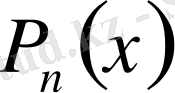 полиномының түрін анықтау үшін
полиномының түрін анықтау үшін
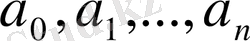 коэффициенттерін анықтау қажет. Коэффициенттерін анықтауды қарастырайық:
коэффициенттерін анықтау қажет. Коэффициенттерін анықтауды қарастырайық:
а)
 -ді анықтау үшін (3) -те
-ді анықтау үшін (3) -те
 десек:
десек:
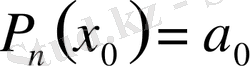 , екінші жағынан, (2) бойынша
, екінші жағынан, (2) бойынша
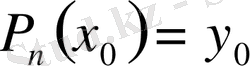 , сонымен
, сонымен
 .
.
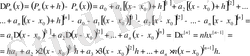 в)
в)
 анықтау үшін
анықтау үшін
 полиномының бірінші ретті ақырғы айырмасын қарастырайық:
полиномының бірінші ретті ақырғы айырмасын қарастырайық:
Мұнда
 десек, онда
десек, онда
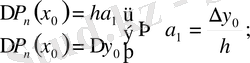 .
.
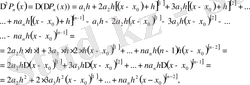 с)
с)
 коэффициентін анықтау үшін,
коэффициентін анықтау үшін,
 екінші ақырғы айырмасын қарастырамыз:
екінші ақырғы айырмасын қарастырамыз:
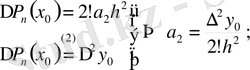 мұнда
мұнда
 десек, онда:
десек, онда:
Осы үрдісті әрі қарай жалғастыра отырып, (3) полиномының кезкелген
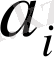 -ші коэффициентін анықтауға болады:
-ші коэффициентін анықтауға болады:
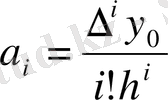 , (
, (
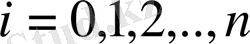 ) (4)
) (4)
Табылған коэффициенттердің мәндерін (3) -ке қойсақ:
 Немесе жалпыланған дәрежені ашып жазсақ:
Немесе жалпыланған дәрежені ашып жазсақ:
(5), (6) Ньютонның 1-ші интерполяциялық формуласы деп аталады.
(5) немесе (6) полиномға қойылған (2) шартты қанағаттандырады:
1) Жақшаларды ашып жазсақ, полиномның дәрежесі n -нен артық болмайтынына көз жеткіземіз.
2)
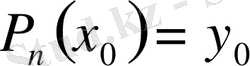 . Енді
. Енді
 десек, онда:
десек, онда:
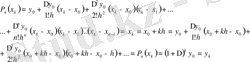
Сонымен,
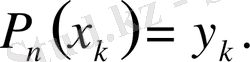
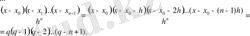
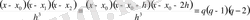 Практикада есептеуді жеңілдету үшін, Ньютонның (5), (6) түріндегі формуласында
Практикада есептеуді жеңілдету үшін, Ньютонның (5), (6) түріндегі формуласында
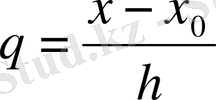 белгілеуін қолданамыз.
белгілеуін қолданамыз.
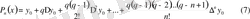
(7) формуласында
 болғанда сызықтық интерполяция
болғанда сызықтық интерполяция
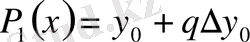 ,
,
 болғанда квадраттық интерполяция
болғанда квадраттық интерполяция
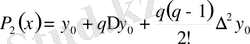 аламыз.
аламыз.
Сонымен, Ньютонның бірінші интерполяциялық формуласы кез-келген
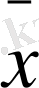 нүктесі
нүктесі
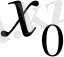 -дің аймағында орналасқан жағдайда, кез-келген
-дің аймағында орналасқан жағдайда, кез-келген
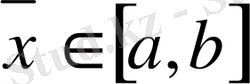 үшін
үшін
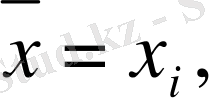
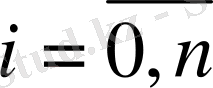 нүктесінде функцияның мәнін жуықтап есептеу үшін қолданылады.
нүктесінде функцияның мәнін жуықтап есептеу үшін қолданылады.
1. 5. 2 Ньютонның екінші интерполяциялық формуласы
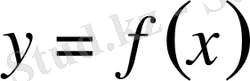 функциясы
функциясы
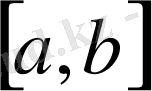 аралығында кесте түрінде берілген.
аралығында кесте түрінде берілген.
Функцияның интерполяциялау нүктелерінен өзге нүктелердегі мәнін жуықтап есептеу қажет. Интерполяциялау тораптары бір-бірінен бірдей қашықтықта орналасқан болсын:
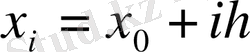 ,
,
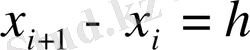 - const,
- const,
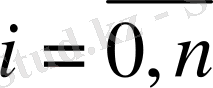 .
.
Интерполяциялаушы полиномды төмендегідей түрде іздейміз:

Жалпыланған дәреженің анықтамасын пайдаланып:
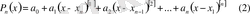
(1) немесе (2) полиномдары төмендегідей екі шартты қанағаттандыруы қажет:
1) Полиномның дәрежесі n -нен артық емес.
2) Интерполяциялау түйіндерінде полиномның қабылдайтын мәндері функцияның кестелік мәндерімен бірдей болуы керек.
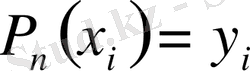 және
және
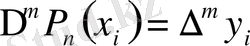 ,
,
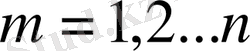 .
.
Полиномының түрін анықтау үшін a 0 , a 1 , …, a n коэффициенттерін анықтау керек:
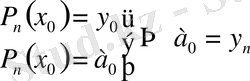 а)
a
0
коэффициентін анықтау үшін (2) -де
а)
a
0
коэффициентін анықтау үшін (2) -де
 ,
,
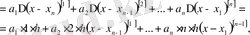
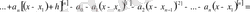
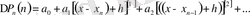 в)
a
1
коэффициентін анықтау үшін
в)
a
1
коэффициентін анықтау үшін
 қарастырамыз:
қарастырамыз:
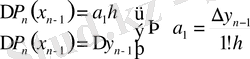 мұнда
мұнда
 болсын, онда:
болсын, онда:
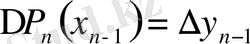 .
.
с) а
2
коэффициентін анықтау үшін полиномның
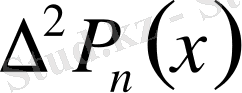 қарастырамыз:
қарастырамыз:
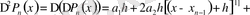
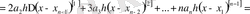
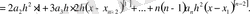
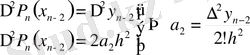 Мұнда
Мұнда
 болсын, онда:
болсын, онда:
Осы үрдісті әрі қарай жалғастыра отырып,
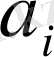 коэффициентін анықтау үшін
коэффициентін анықтау үшін
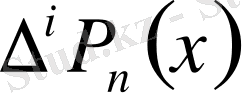 -ті қарастырып, онда
-ті қарастырып, онда
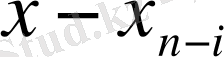 десек, онда:
десек, онда:
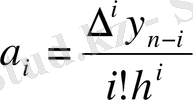 , (3)
, (3)
(3) формула бойынша анықталған
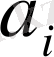 коэффициенттерінің мәндерін (2) -ге қойсақ:
коэффициенттерінің мәндерін (2) -ге қойсақ:
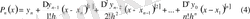 ,
,
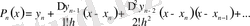 немесе
немесе
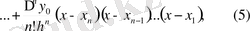
(4), (5) формулаларын Ньютонның екінші интерполяциялау формуласы деп атайды.
Сонымен,
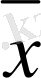 нүктесі
нүктесі
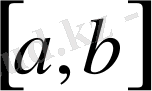 аралығының
аралығының
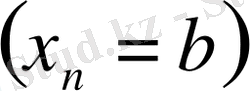 нүктесіне жақын орналасса, функцияның мәнін
нүктесіне жақын орналасса, функцияның мәнін
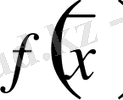 жуықтауын есептеу үшін Ньютонның екінші интерполяциялау формуласын қолдану жақсы нәтиже береді (есептеу кезінде жіберген қатенің шамасы мейлінше аз болады) .
жуықтауын есептеу үшін Ньютонның екінші интерполяциялау формуласын қолдану жақсы нәтиже береді (есептеу кезінде жіберген қатенің шамасы мейлінше аз болады) .
(4), (5) формулаларын практикада қолдану үшін
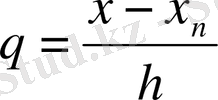 белгілеуін
белгілеуін
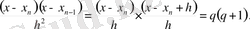 енгізіп, ықшам түрге келтіруге болады:
енгізіп, ықшам түрге келтіруге болады:
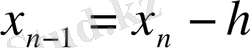

1. 5. 3 Функцияның кестесін тығыздау
Практикада, кесте түрінде берілген функцияның қасиеті туралы толығырақ мағлұмат алу үшін, оның өзгеру бөлігіндегі интерполяциялау түйіндерін көбейтуге тура келеді. Ол үшін интерполяциялау әдісін қолдануға болады.
Бұл операцияны функцияның кестесін тығыздау немесе субтабуляциялау деп атайды.
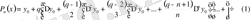 Есептеу жұмыстарын жүргізуді жеңілдету үшін Горнер сызбасы қолданылады. Ньютонның бірінші интерполяциялық формуласын Горнер сызбасының көмегімен төмендегі түрде қолдану ыңғайлы:
Есептеу жұмыстарын жүргізуді жеңілдету үшін Горнер сызбасы қолданылады. Ньютонның бірінші интерполяциялық формуласын Горнер сызбасының көмегімен төмендегі түрде қолдану ыңғайлы:
.
Мұнда ақырғы айырмалар кестесі құрылады. Ақырғы айырмалардың мәндері нольге жуық болуы мүмкін, онда да оларды ескермеуге болады.
Практикада функцияның кестесін тығыздау үшін көп жағдайда интерполяциялық формуласының стандартты түрлері қолданылады (сызықтық, квадраттық, интерполяциялық формулалар) .
Мысал:
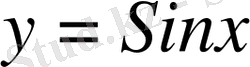 функциясы
функциясы
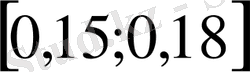 аралығында
аралығында
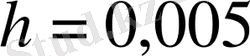 қадаммен берілген. Осы кестені
қадаммен берілген. Осы кестені
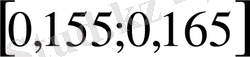 аралығында
аралығында
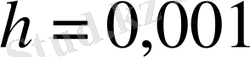 қадаммен тығыздау керек.
қадаммен тығыздау керек.
Бұл кестеде
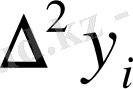 тұрақты деп қарастыруға болады. Олай болса, функция кестесін тығыздау үшін стандартты формуланы қолдануға болады (квадраттық интерполяция) .
тұрақты деп қарастыруға болады. Олай болса, функция кестесін тығыздау үшін стандартты формуланы қолдануға болады (квадраттық интерполяция) .
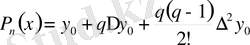
Есептеуді Ньютонның бірінші интерполяциялық формуласы бойынша жүргізейік:
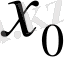 ретінде
ретінде
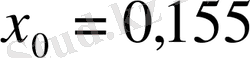 деп алайық .
деп алайық .
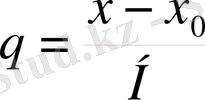 ;
;
Есептеуді төмендегі блок-сызба бойынша ұйымдастыруға болады, мұндағы:
 жаңа аралық,
Н1
- жаңа қадам,
хО
- жаңа аралықтың алғашқы нүктесі,
у1
- кесте түрінде берілген функцияның 1-ші ретті ақырғы айырмасы,
у2
- сәйкес 2-ші ретті ақырғы айырмасы.
жаңа аралық,
Н1
- жаңа қадам,
хО
- жаңа аралықтың алғашқы нүктесі,
у1
- кесте түрінде берілген функцияның 1-ші ретті ақырғы айырмасы,
у2
- сәйкес 2-ші ретті ақырғы айырмасы.
Сурет 1. 2 Субтабуляциялау блок - сызбасы
Нәтижесіндетиже кесте:
1. 5. 4 Ньютонның интерполяциялық формуласының қалдық мүшелері
Ньютонның формуласын қарастырған кезде интерполяциялау түйіндері бір-бірінен бірдей қашықтықта орналасқан деп ұйғарамыз,
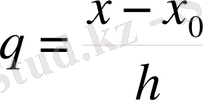
Лагранждың қалдық мүшесінің формуласында:
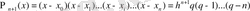 екенін ескерсек, онда:
екенін ескерсек, онда:
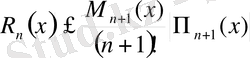

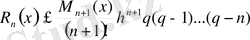 (1) формуласын аламыз. Мұндағы
(1) формуласын аламыз. Мұндағы
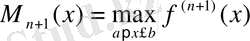
Сонымен Ньютонның І-ші интерполяциялық формуласының қалдық мүшесі (1) формуламен анықталады.
Дәл осылай Ньютонның ІІ-ші интерполяциялық формуласының қалдық мүшесін анықтаймыз:
(2)
Жіберілген қатенің шамасына
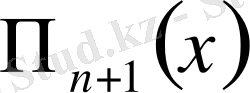 тигізетін ықпалы үлкен, әсіресе қарастырылып отырған
тигізетін ықпалы үлкен, әсіресе қарастырылып отырған
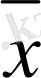 нүктесі интерполяциялау түйіндерінің ортасында орналасса,
нүктесі интерполяциялау түйіндерінің ортасында орналасса,
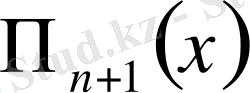 шамасы кішірейеді.
шамасы кішірейеді.
Сондықтан,
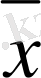 нүктесі екі тораптық нүктенің ортасында орналасса, онда тораптық түйіндердің саны жұп етіп алған тиімді
нүктесі екі тораптық нүктенің ортасында орналасса, онда тораптық түйіндердің саны жұп етіп алған тиімді
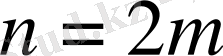 . Ал егер
. Ал егер
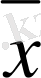 мәні тораптық түйіндердің біреуіне жақын орналасса, онда тораптық түйіндер санының тақ болғаны, яғни
мәні тораптық түйіндердің біреуіне жақын орналасса, онда тораптық түйіндер санының тақ болғаны, яғни
 болғаны жақсы нәтиже береді.
болғаны жақсы нәтиже береді.
Ньютонның интерполяциялық формуласын құру кезінде нольге жуық ақырғы айырмаларды ескермеуге болады. Сондықтан, есептеуде Ньютон полиномының мүшелерін қиюға рұқсат етіледі, әсіресе берілген дәлдікпен есептеуді жүргізген кезде тұрақты деп санауға болатын ақырғы айырмалармен тұрған мүшелерді алып тастауға болады.
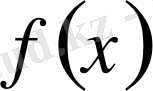 және
және
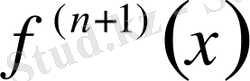 функциясы үзіліссіз екендігін ескеріп,
h
-тың өте кішкене мәндері үшін
функциясы үзіліссіз екендігін ескеріп,
h
-тың өте кішкене мәндері үшін
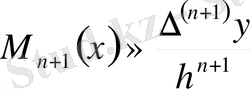 (3)
(3)
алуға болады, мұндағы
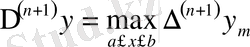 , яғни
, яғни
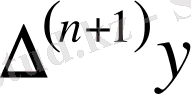 (
n+1
) -ші ретті ақырғы айырмалардың ішіндегі ең үлкені (модулі бойынша) .
(
n+1
) -ші ретті ақырғы айырмалардың ішіндегі ең үлкені (модулі бойынша) .
Сонымен, Ньютонның бірінші формуласының қалдық мүшесі:
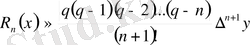 , (4)
, (4)
Ньютонның екінші формуласының қалдық мүшесі:
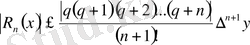 , (5)
, (5)
1. 6 Лагранж интерполяциялық формулалары
1. 6. 1 Лагранж интерполяциялық формуласы
Біз бұған дейін интерполяциялау түйіндерінің ара қашықтықтары
 деп қарастырдық, енді интерполяциялау түйіндерінің бір-бірінен ара-қашықтықтары әртүрлі болсын.
деп қарастырдық, енді интерполяциялау түйіндерінің бір-бірінен ара-қашықтықтары әртүрлі болсын.
Бізге
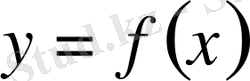 функциясы кесте түрінде берілген болсын.
функциясы кесте түрінде берілген болсын.
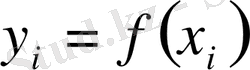 ,
,
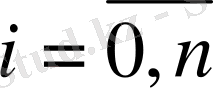
 Дәрежесі
n
-нен артық емес және интерполяциялау түйіндерінде қабылдайтын мәндері, функцияның осы нүктелердегі мәндерімен бірдей болатын қайсы бір
Дәрежесі
n
-нен артық емес және интерполяциялау түйіндерінде қабылдайтын мәндері, функцияның осы нүктелердегі мәндерімен бірдей болатын қайсы бір
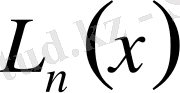 полиномының түрін анықтау керек, яғни
полиномының түрін анықтау керек, яғни
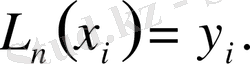
Сурет 1. 3
Алдымен төмендегідей есепті қарастырайық:
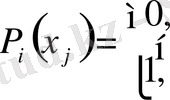
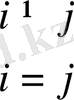 (1) болатындай
(1) болатындай
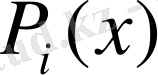 полиномының түрін анықтайық.
полиномының түрін анықтайық.
Ізделініп отырған
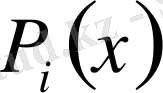 полиномы
n
нүктесінде нольге айналады, олай болса ол полиномды төмендегідей түрде анықтауға болады:
полиномы
n
нүктесінде нольге айналады, олай болса ол полиномды төмендегідей түрде анықтауға болады:
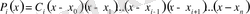 (2)
(2)
С і тұрақты коэффициент.
(2) -де
 ,
,
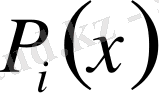 =1.
=1.
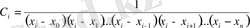
С і -дің мәнін (2) -ге қойып:
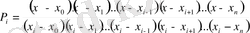 , (3)
, (3)
Интерполяциялау қадамы тұрақты болмаған жағдайда функцияның мәнін жуықтап есептеу үшін интерполяциялаушы формуланы төмендегідей іздейміз:
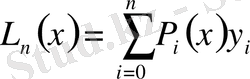 , (4)
, (4)
Бұл полином төмендегідей шарттарды қанағаттандырады:
- полиномның дәрежесіn-нен артық емес.
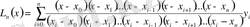 , (5)
, (5)
(5) Лагранждың интерполяциялау формуласы деп аталады.
Мысалы: Функция кесте түрінде берілген. Функция мәнін жуықтап есептейтін полиномның түрін анықтаңдар.
n= 2
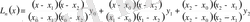
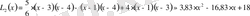
1. 6. 2 Лагранж интерполяциялық формуласының ықшамдалған түрі
Практикада Лагранж интерполяциялық формуласын қолдану үшін төмендегідей белгілеу енгізіледі:
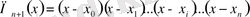 , (1)
, (1)
(1) -ді х бойынша дифференциалдасақ,
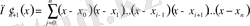 , (2)
, (2)
(2) -де
 , онда:
, онда:
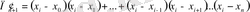 , (3)
, (3)
(1) мен (3) -ті (5) формулаға қойсақ:
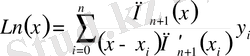 , (4)
, (4)
(4) түріндегі Лагранж интерполяциялық формуласы практикада функцияның мәнін жуықтап есептеу қолданған тиімді, мұнда
 .
.
Сурет 1. 4 Лагранж интерполяциялық формуласының блок - сызбасы
1. 6. 3 Лагранж интерполяциялық формуласы бойынша есептеуді ұйымдастыру
Лагранж интерполяциялау формуласымен функцияның мәнін жуықтап есептеуді жеңілдету үшін y i -дің коэффициенттерін төмендегідей түрде белгілейік:
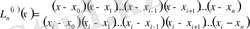 , (1)
, (1)
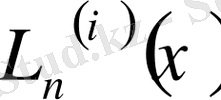 - Лагранж коэффициенттері деп аталады.
- Лагранж коэффициенттері деп аталады.
Сонымен Лагранж интерполяциялық формуласы:
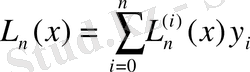 (2)
(2)
Мұндағы
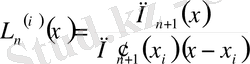 , (3)
, (3)
Лагранж коэффициенттерінің формасы (3) бүтін сызықтық ауыстыру
 -ға қатысты инвариантты.
-ға қатысты инвариантты.
Шындығында да
 ,
,
 және
және
 және
және
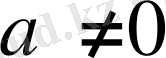
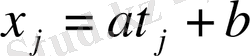 мәндерін (1) -ге қойсақ:
мәндерін (1) -ге қойсақ:
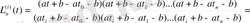
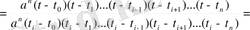
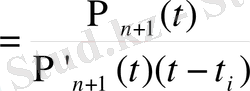 (3`)
(3`)
Мұндағы
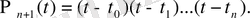
Енді Лагранж коэффициенттерін есептеу сызбасын қарастырайық. Коэффициенттерді есептеу үшін төмендегідей сызба қолданылады:
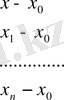
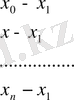
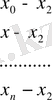

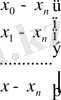 (4)
(4)
Бірінші жатық жолының элементтерінің көбейтіндісін
P
0
, екінші жатық жолының көбейтіндісін
P
2
, т. с. с. белгілейік. Негізгі диогнальдың элементтерінің көбейтіндісі
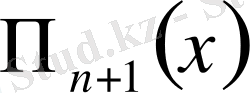 болады.
болады.
Сонымен,
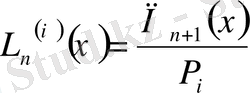 ,
,
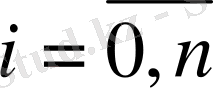 (5)
(5)
Ал,
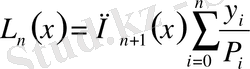 , (6)
, (6)
Егер интерполяциялау тораптары бір-бірінен бірдей қашықтықта орналасса, онда (6) формуласы қарапайым түрге келтіріледі немесе практикада төмендегі түрде қолданылады:
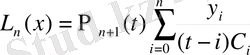 , (7)
, (7)
мұндағы
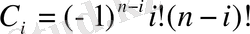
Есептеуді жеңілдету үшін төмендегі сызбаны қолданамыз:
1. 6. 4 Бірдей қашықтықта орналасқан түйіндер үшін Лагранж интерполяциялық формуласы
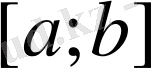 кесіндісі
кесіндісі
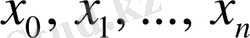 нүктелері арқылы тең
нүктелері арқылы тең
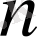 бөлікке бөлінсін:
бөлікке бөлінсін:
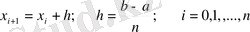
Бірдей қашықтықта орналасқан түйіндер үшін Логранж интерполяциялық формуласын қарастырайық:
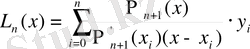 (1)
(1)
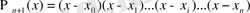 ;
;
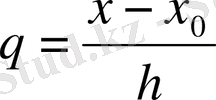 ;
;
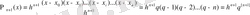 ;
;
Немесе
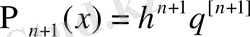 (2)
(2)
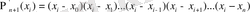
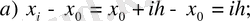
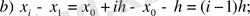
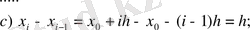
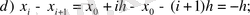
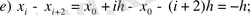
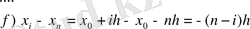
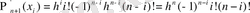 (3)
(3)
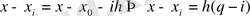 (4)
(4)
(3), (3), (4) -ті (1) -ге қойсақ:
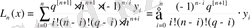 (5)
(5)
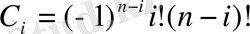
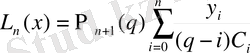
1. 6. 5 Лагранж интерполяциялық формуласының қалдық мүшесін бағалау
Интерполяциялау тораптарында функцияның қабылдайтын мәндері
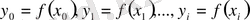 , болатын полином
, болатын полином
 -ді Лагранж полиномын қарастырғанбыз. Енді онық қалдық мүшесін анықтайық
-ді Лагранж полиномын қарастырғанбыз. Енді онық қалдық мүшесін анықтайық
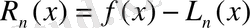 (1)
(1)
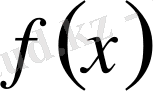 функциясы
функциясы
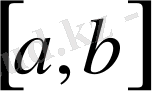 аралығында
аралығында
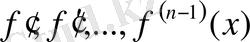 туындылары бар. Көмекші
туындылары бар. Көмекші
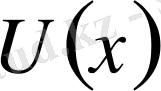 функциясын төмендегідей түрде енгіземіз:
функциясын төмендегідей түрде енгіземіз:
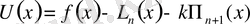 (2)
(2)
Мұндағы
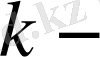 тұрақты коэффициент.
тұрақты коэффициент.
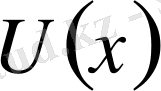 функциясы
функциясы
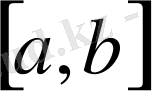 аралығында «
аралығында «
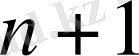 » нүктесінде нольге айналады.
» нүктесінде нольге айналады.
(2) -дегі
k
-коэффициентін
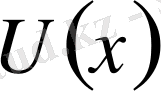 функциясы
функциясы
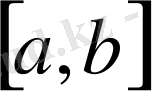 аралығының «
аралығының «
 »-ші нүктесінде де нольге айналатындай етіп таңдап аламыз.
»-ші нүктесінде де нольге айналатындай етіп таңдап аламыз.
Анықтық үшін
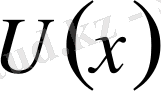 функциясы
функциясы
 нүктесінде нольге айналады деп ұйғарсақ, яғни:
нүктесінде нольге айналады деп ұйғарсақ, яғни:
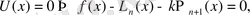 мұндағы
мұндағы

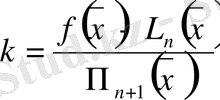 (3)
(3)
Сонымен,
k
-ның мұндай мәнінде
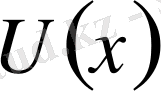 функциясы
функциясы
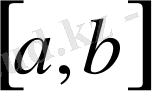 аралығының
аралығының
 нүктесінде нольге айналады, яғни
нүктесінде нольге айналады, яғни
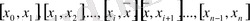 кесіндінің ұштарында
кесіндінің ұштарында
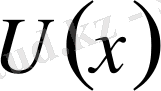 функциясы нольге айналады. Кесінділер саны
функциясы нольге айналады. Кесінділер саны
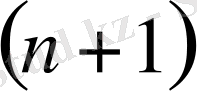 .
.
Осы кесінділердің әрқайсысына математикалық анализден белгілі Ролль теоремасын қолданайық, онда
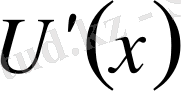 -ның (
-ның (
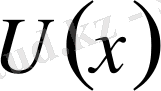 функциясының бірінші ретті туындысы)
функциясының бірінші ретті туындысы)
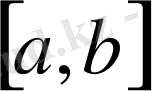 аралығының
аралығының
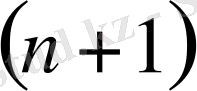 нүктесінде нольге айналады.
нүктесінде нольге айналады.
Ұштарында
 болатындай жаңа кесінділер
болатындай жаңа кесінділер
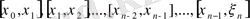
табылады.
Табылған жаңа кесінділерге Роль теоремасын қолдансақ, онда
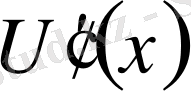 функциясы нольге айналатын
функциясы нольге айналатын
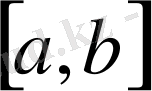 аралығында
n
нүкте табылады, яғни
аралығында
n
нүкте табылады, яғни
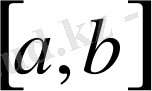 -да
-да
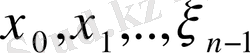 нүктелері анықталады.
нүктелері анықталады.
Сонымен ұштарында
 функциясы нольге айналатын төмендегідей кесінділер табылады:
функциясы нольге айналатын төмендегідей кесінділер табылады:
 -барлық саны «
n-1
»
-барлық саны «
n-1
»
Осы үрдісті әрі қарай жалғастыра отырып, ең ақырында
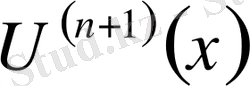 функциясының
функциясының
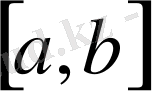 кесіндісінің тым болмаса бір нүктесінде нольге айналатындығын анықтаймыз, мысалы бір
кесіндісінің тым болмаса бір нүктесінде нольге айналатындығын анықтаймыз, мысалы бір
 нүктесінде
нүктесінде
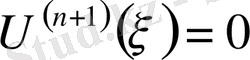 (4)
(4)
Енді
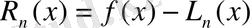 формуласына қайтадан оралайық.
формуласына қайтадан оралайық.
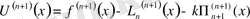
Мұндағы
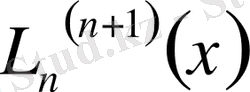 =0, себебі
=0, себебі
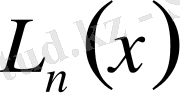 n
-ші ретті полином, ал оның
n+1
-ші ретті туындысы нольге тең.
n
-ші ретті полином, ал оның
n+1
-ші ретті туындысы нольге тең.
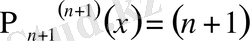
Сонымен,
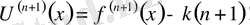

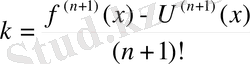 .
.
Енді
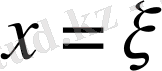 -деп алайық, онда
-деп алайық, онда
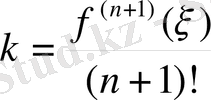 (5)
(5)
(5) пен (3) теңдіктерінің оң жақтарын салыстыра отырып:
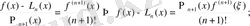
 кесіндісінің кез-келген нүктесі болғандықтан, соғңы тұжырымды төмендегідей түрде жазуға болады:
кесіндісінің кез-келген нүктесі болғандықтан, соғңы тұжырымды төмендегідей түрде жазуға болады:
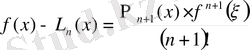 , (6)
, (6)
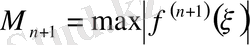 ,
,
 белгілеуін енгізсек, онда:
белгілеуін енгізсек, онда:
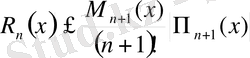 (7)
(7)
(7) - Лагранж интерполяциялық формуласының қалдық мүшесін анықтайды.
1. 7 Гаусс интерполяциялық формулалары
1. 7. 1 Гаусстың бірінші және екінші интерполяциялық формулалары
Бізге
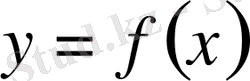 функциясы кесте түрінде берілген:
функциясы кесте түрінде берілген:
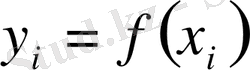 ;
;
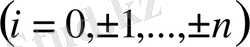 , (1)
, (1)
Алдымен Гаусстың интерполяциялық формуласын қорытып шығарайық. Аралықтың
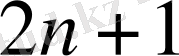 бірдей қашықтағы интерполяциялық түйіндері бар болсын.
бірдей қашықтағы интерполяциялық түйіндері бар болсын.
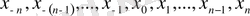 , мұнда
, мұнда
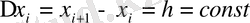
Бізге
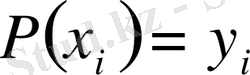 ,
,
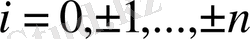 болатындай, дәрежесі 2n -нен артпайтын
болатындай, дәрежесі 2n -нен артпайтын
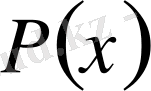 полиномын құрастыру керек.
полиномын құрастыру керек.
Соңғы шарттан барлық
i
және
k
мәндері үшін
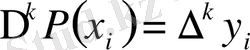 , (1)
, (1)
екені шығады. Полиномды мына түрде іздейміз:
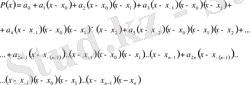
(2)
Жалпыланған дәрежені енгізе отырып,
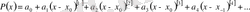
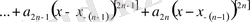 (3)
(3)
аламыз.
Ньютонның интерполяциялық формуласын қорыту үшін пайдаланатын әдісті коэффициенттерді анықтау үшін қолданып
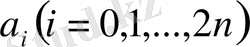 және (1) формуласын ескере отырып, төмендегі формулаларды аламыз:
және (1) формуласын ескере отырып, төмендегі формулаларды аламыз:
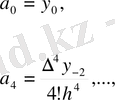
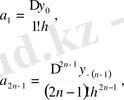
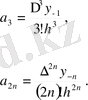
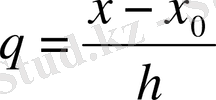 айнымалысын енгізе отырып және (3) формуласына сәйкес ауыстырулар жасап, Гаусстың бірінші интерполяциялық формуласын аламыз:
айнымалысын енгізе отырып және (3) формуласына сәйкес ауыстырулар жасап, Гаусстың бірінші интерполяциялық формуласын аламыз:
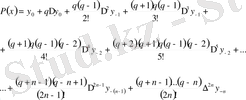 (4)
(4)
немесе қысқаша түрде
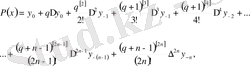 (4′ )
(4′ )
Мұнда
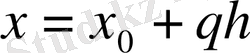 және
және
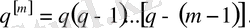
Гаусстың бірінші интерполяциялық формуласы жоғарғы центрлік айырымдар
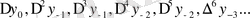 қолданылады.
қолданылады.
Сол сияқты төменгі центлік айырымдардан тұратын
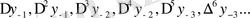 Гаусстың екінші интерполяциялық формуласын алуға болады.
Гаусстың екінші интерполяциялық формуласын алуға болады.
 Гаусстың екінші интерполяциялық формуласы мына түрде болады:
Гаусстың екінші интерполяциялық формуласы мына түрде болады:
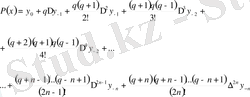 (5)
(5)
немесе қысқаша түрде
 (5′ )
(5′ )
мұнда
 .
.
Гаусстың екінші интерполяциялық формуласында төменгі центрлік айырымдар қолданылады.
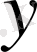

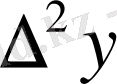

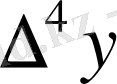
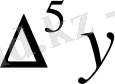
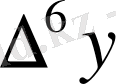
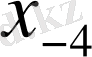
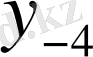
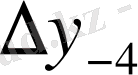
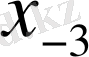
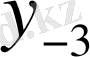
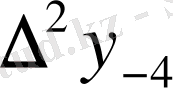

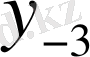
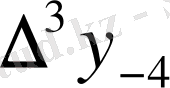
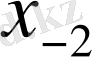
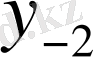

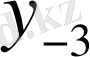
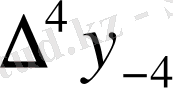

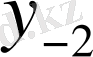

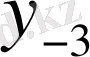
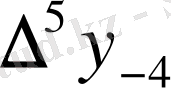
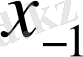
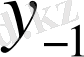

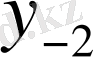

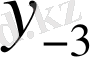
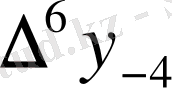



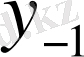



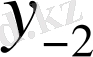



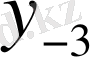
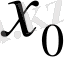


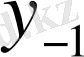

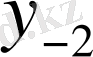
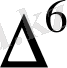
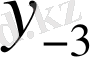



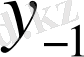

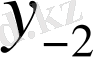




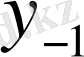
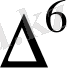
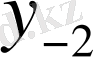





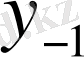
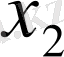
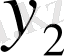





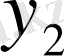


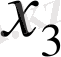
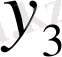

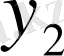

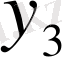
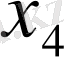

Центрік айырымдар кестесі
1. 8 Стирлинг интерполяциялық формуласы
Гаусстың бірінші және екінші интерполяциялық формулаларының орта арифметикалық шамасын алғаннан соң, Стирлинг формуласын аламыз:
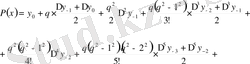
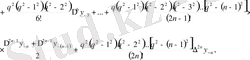
мұндағы
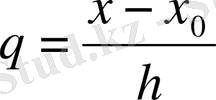 .
.
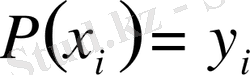 ,
,
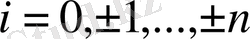 екенін оңай көруге болады.
екенін оңай көруге болады.
Ақырғы айырымдарды есептеу үшін центрлік айырымдар кестесі қолданылады.
2 «ФУНКЦИЯНЫ ИНТЕРПОЛЯЦИЯЛАУ» КУРС ҚҰРУ
2. 1 Электрондық курстың құрылымы
... жалғасыЭлектрондық курс - бұл компьютер арқылы оқу курсынын немесе оның кез-келген бөлімін өз бетінше меңгеруге көмектесетін бағдарламалық-методикалық кешен. Электрондық курс - студентке қажет материалды жеке меңгеруге арналған күрделі, көпсатылы жүйе, оқулықтың қажетті бөлімдерін қайталап, игеру тәсілі мен логикасын да өзіне тән етіп таңдап алып, осы сәтте ең керек деген материалдарды қарап шығуға мүмкіндік береді. Оның гипермәтіні накты құрылымдардан тұрады да, бір-бірімен тығыз байланысқан ықшам логикалық жүйе болып табылады.
Электрондық курс көбінесе екі бөлімнен қүралады:
1) презентациялық бөлімі;
2) оқу құралының негізгі ақпаратынан құралған тапсырма бөлімі.
Электрондық курс төмендегідей қасиеттермен сипатталуы қажет:
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz