Суреттерді бір координаттық жүйеден басқа жүйеге ауыстыру әдістері

Пән: Геология, Геофизика, Геодезия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 12 бет
Таңдаулыға:

Әл - Фараби атындағы Қазақ Ұлттық университеті

География және табиғатты пайдалану факультеті Картография және геоинформатика кафедрасы

СӨЖ

Тақырыбы: Суреттерді бір координаттық жүйеден басқа жүйеге ауыстыру әдістері

Тексерген: Құдайбергенов М

Орындаған: Ходжаева Р

Алматы, 2016

ЖОСПАР

ЖОСПАР:

КІРІСПЕ

ЖОСПАР:

НЕГІЗГІ БӨЛІМ

ЖОСПАР: 1

Кеңістік координаттары

ЖОСПАР: 2

Картографиядағы координата жүйелері

ЖОСПАР: 3

Координаталарды өзгерту

ЖОСПАР: 4

Проекцияны өзгерту

ЖОСПАР: 5

AutoCAD Map 3D бағдарламасында координаттар жүйесін өзгерту

ЖОСПАР:

ҚОРЫТЫНДЫ

ЖОСПАР:

ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР

КІРІСПЕ

Координаттар (лат. co - бірге және ordіnatus - тәртіптелген, анықталған) - жазықтықтағы, кез келген беттегі не кеңістіктегі нүктенің орнын анықтайтын сандар. Ғылымға, ең әуелі, аспан сферасындағы не Жер шары бетіндегі нүктенің орнын (ендік пенбойлық) анықтайтын астрономиялық және географиялық кординаттар енді. 17 ғасырда Р. Декарт кординаттар әдісі арқылы геометрия мен математикалық анализдің арасындағы өзекті байланысты ашты.

Механикада, математикада физикада, т. б. салаларда сфералық Координаттар (θ, ϕr, ), цилиндрлік Координаттар (, zϕ, ρ), эллипсоидтық координаттар жиі қолданылады. Кеңістіктегі біртекті координаттар жазықтықтағы координаттар сияқты енгізіледі.

Декарттық координаттар жүйесі - евклидтік кеңістіктегі түзу сызықты координаттар жүйесі;

Түзу сызықты координаттар- координаттар бас нүктесі және осы нүктеде қиылысатын түзу сызықты координаттар осьтері бойынша анықталатын координаттар;

Тікбұрышты координаттар - барлық осьтері өзара перпендикуляр болатын түзу сызықты координаттар;

Сфералық координаттар - барлық осьтері өзара перпендикуляр болатын түзу сызықты координаттар; [2]

НЕГІЗГІ БӨЛІМ

Кеңістік координаттары

Координаттар деп - кеңістікте, жазықтыққа берілген нүктенің тұрған орнын анықтайтын сандарды айтады.

Тік бұрышты немесе декарт координаттары (1-сурет) . Бұл бір-біріне перпендикуляр X (абсцисса) және Ү (ордината) тік бұрышты сызықгар құрайтын, “0” нүктесінде түйісетін немесе +/- белгімен белгіленетін жазықтық координаттар түрлерін айтады. Бір беткейде жатқан үш өлшемді X, Ү, Z координаттарының басы “0- ге” түйіседі.

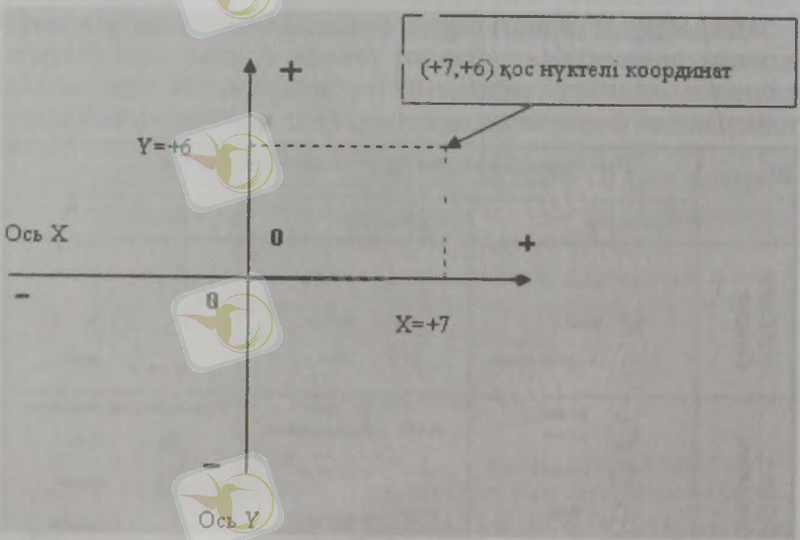
1-сурет. Тік бұрышты координаттар жүйесі

Геодезиялық жұмыстарда бастапқы нүкте ретінде қабылданған бір нүкте арқылы анықтау үшін қолданатын координаталар жүйесін полюстік координаттар дейді. Нүктелердің жазықтықтағы орны қарастырылатын бұл жүйеде нүктелердің орны екі координатамен; а- полюстік осімен анықталатын нүктеге қарай бағытталған кесіндінің арасындағы горизонталь бұрышпен; д - полюстен анықталатын нүктеге дейінгі горизонталь арақашыктықпен анықталады. Полюстік бүрыштар 0°-ден 360°-қа дейін өлшенеді. Бұл координаталар жүйесі теодолиттік түсіру және жобадағы барлау ұңғымасының горизонталь жазьқтықтағы орнын табу кезінде қолданылды.

Бұдан басқа сфералық, элпипсойдтық координаталар т. б. бар. Бұлар ГАЖ-дың алдына қойылған мәселелерді шешуге байланысты қолданылады.

Гаусс-Крюгер координатасы - тең бүрышты картографиялық проекция арқылы енгізілетін жазықгықтағы тікбұрышты координаттар жүйесі. Мұнда, жер эллипсойды жазықтық зоналармен және меридиандармен шектеледі.

Зоналар Гринвич меридианынан бастап батыстан шығысқа қарай нөмірленеді. Абсцисса (X) меридиан осінің корінісі, ал ордината (У) - экватор көрінісі. Бірінші 6°-тық зонадағы остік меридиандағы шығыс бойлық 30°-ға тең, ал екіншісінде 90°- ға тең. Остік меридиан экватордың қиылысқан жері, бұл координаттар басы, ол X = 0 м, У = 5 м болады. Зона номері “У” алдында орналасқан. Остік мериаңдағы X шамасы элипсоидтағы меридианның доға үзындығының экватормен берілген парралель арақашықгығына тең. Масштабы 1:5000 топографиялық түсірімде 3°-тық зона пайдаланылады. ^[1]

Картографиядағы координата жүйелері

Координаталар жүйесі жердегі бағыт пен арақашықтықты анықтау үшін қажет. Ендік пен бойлықты пайдаланып, координаттардың географиялық жүйесі Жердің сфералық бетінде немесе аралық глобуста орналасқан нысандардың орнын анықгау үшін қолайлы. Осы глобустан біз көбінесе екі өлшемді карталармен жұмыс істейтіндіктен, әртүрлі проекцияларға сәйкес келетін координаттардың бір немесе бірнеше жүйелері қажет етіледі. Мысалы, геодезиялық, астрономиялық, тік бұрышты координаттар жүйесі. Координатгардың мұндай жүйелері жазықтықта координаттардың картографиялық ( геодезиялық ) тік бұрышты жүйелері (cartografical (geodetic) rectongulor sustems of coordinates) деп аталады, олар жазық карталардағы нысандар орнын нақгы көрсетеді (2-сурет) .

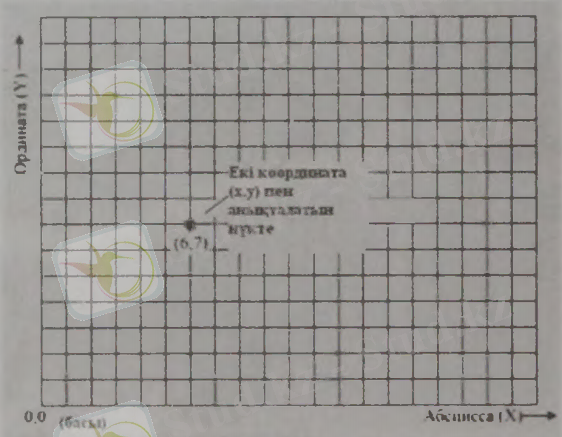
2-сурет. Декарттық координаттар жүйесі

Тік бұрышты координаттардың негізгі жүйесі графиктік жане сандық бұрыштармен жұмыс істеу кезінде ыңғайлы. Ол екі сызықтан: абциссалар мен ординатгардан тұрады. Абцисса 0-ден бастап, яғни координат басынан, екі бағытта шексіз жалғасатын сандардың бірдей таралуын құрайтын көлденең сызық. Шамаларды X координаталары деп аталады, олар оң және теріс болады. Екінші сызық, ордината, сол бастапқы нүктеде оң және теріс бағыттарда тік бұрышты қозғалысты қамтамасыз етеді. Бұл екі координата кез келген нүкте мен нысанның орналасқан жерін (Х, У) шамаларын анықтауға мүмкіндік береді. Геоақпараттық жүйелерде - координаттарды анықтау үшін пайдаланатын қондырғылар мен дигитайзерлер қарапайым декартты координаттар жүйесіне негізделген.

Көптеген ГАЖ-да проекция жүйесі мен координаттар Меркатордың көп таралған универсалды көлденеңі (UTM) қолданылады (3-сурет) . Ол дистанциялық (аралық) зондтаумен, топографиялық карталарды дайындауда, табиғи ресурстардың деректерінің базасын құруда пайдаланылады. Өйткені, ол көптеген елдерде және ғылыми байланыспен қабылданған метрикалық жүйеде нақты өлшеулерді камтамасыз етеді. Онда өлшеудің негізгі бірлігі метр болып табылады.

UTM жер бетін ұзындығы 6° бойынша ендіктің 60°-тық белдеуінде бөледі. Олардың әрқайсысы оңтүстік ендіктің 80°-нан солтүстік ендіктің 84°-қа дейін өтеді. Барлық координатгар оң болу үшін, UTM-де координаттардың 2 басы болады: біреуі - экваторда ( солтүстік ) және екінші - оңтүстік ендіктің 80°-ші параллелінде ( оңтүстік ) . Бұл белдеулер шығыс бағытта 180° меридианнан басталып номерленген. Жер беті градусты ендік бойынша бөлінеді.

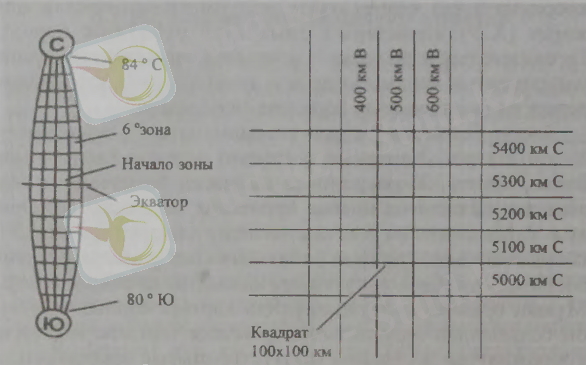
3-сурет. Меркатордың универсалды көлденең

координатты жүйесі

Әрбір секция белдеулер мен қатардың қиылысуынан пайда болады және сандар мен әріптердің комбинацияларымен (басындағыдай - оңнан солға қарай оқылады) белгіленеді, сондықтан жер шарының ұсақ учаскелерін бөлуге болады. ^[1]

Координаталарды өзгерту

Карталар жазық бетке проекцияланған сфералық беттің көрінісі ретінде қабылданады. Ондағы трансформацияланған географиялық мәліметтердің барлығының пішіндері (аудан, арақашықтық, бұрыштар) деформацияланған. Цифрлау кезінде бұл күрделі проекция декарт координаталары жиынтығына құрайды. Осыны істердің алдында, бағдарламаға пайдаланған проекция типін және координатторлары мен зоналары жайлы нақты мәліметтерді хабарлау қажет. Осы іс-шаралар картаны өзінің енгізуіне дейінгі проекция түрінің өзгеруіне мүмкіндік береді.

Шын мәнінде ГАЖ осындай бірқатар өзгерулерді жүзеге асырады, дигитайзердің декарт координаталарынан картографиялық проекцияның екіөлшемді координаталарына проекциялау үрдісі жүреді, және одан кері картографиялық проекция арқылы сфералық ендік жөне бойлық, координаталарына ауысады. Әрі қарай осы үрдіс шығу құрылғысы үшін декарт координаталарын алу мақсатында пайдаланылады.

Проекциялау кезінде негізгі үш графиктік процестер бір мезгілде жүреді. Олар: а) координата кеңістігіндегі нысанның орнын ауыстыру үшін тасымалдау; б) нысанның өлшемін өзгерту үшін масштабтау; в) координата кеңістігінде нысан бағдарын өзгерту үшін бұру.

Әртүрлі проекциялармен өзгерулерді жүзеге асыру үшін, ГАЖ-дың негізгі жүйесіндегі шеңберінде бірқатар графикгік операцияларды орындау қажет. Ол үш негізгі үрдістен тасымалдау, бұру және масштабтаудан тұрады.

Тасымалдау (саггу) - бұл координата жазықтығындағы бөліктердің немесе бүкіл графикалық объектінің басқа жерге орын ауыстыруы.

Масштабтау (scaling) - өте тиімді әр түрлі масштабтағы карталарды салыстыру және жасау үшін қажет. Ол нысанның барлық координатасын масштаб коэффициентіне көбейту(не бөлу) арқылы орындалады.

Бұру (turn) - проекциялау жөне кері проекциялау үрдісінде кеңінен қолданылады, тригонометрия көмегімен жүзеге асады. Барлық қажетті өзгертулер негізінен үш графиктік операциялар арқылы орындалады. ^[1]

Проекцияны өзгерту

Сақтау және түзету жүйесі тармақтарының негізгі функциясы графиктік және атрибуттық қателерді түзету болып табылса, бір жағынан олар дигитайзер координаттарын нақты әлем координаттарына ауыстыру үшін де пайдаланылады. Көбінесе бағдарламалар енгізілетін карта проекциясын көрсетуді талап етеді (көбінесе растрлық) . Кез келген жағдайда нақты өмірдің координаттар жүйесін талап ететін кез келген сараптау үшін векторлы жүиелерде карта координаттарын өзгерту қажет. Одан басқа, барлық енгізілетін карталар проекциялары бірдей болғандықтан, әртүрлі карталардан алынған жабындарды салыстыру мүмкіндіктерін камтамасыз ету үшін олардың проекциясын қайтадан өзгертуге тура келеді.

Географиялық байланыс үшін картадағы белгілі географиялық координаттары бар тірек нүктелерін пайдаланылады. Дигитайзерден енгізу кезінде қолд аныл атьш нүктелер тіркеу нүктелері деп аталады.

Растрлық бейнелер және карталар үшін екі географиялық байланыстар мүмкіндігі бар: оларды трансформациялауға немесе калибрлеуге болады. Трансформациялау процесі нәтижесінде жаңа жабын пайда болады, олардың пиксел координаттары трансформация жүргізілген проекцияға сәйкес келеді. Калибрлеу нәтижесінде жаңа жабын түзілмейді, ал байланыстыру параметрлері жабын файлдарымен бірге немесе соның ішінде сақталады. Екінші тәсілдің артықшылығы проекцияны қашанда деректерге тиіспей, деректер сапасьш өзгертпей өзгертуге болатынын көрсетеді. ^[1]