Физика – техниканың іргетасын қалаушы білімнің бірі

Пән: Физика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 103 бет
Таңдаулыға:

МАЗМҰНЫ

Кіріспе 4

1 Механика 5

1. 1 Механикалық қозғалыс 5

1. 2 Түзу сызықты қозғалыс 8

1. 3 Қисық сызықты қозғалыс. Нормаль үдеу 13

1. 4 Материалдық нүктенің шеңбер бойымен қозғалысы 15

1. 5 Еркіндік дәрежесі 18

2 Динамика 19

2. 1 Ньютонның бірінші заңы 19

2. 2 Ньютонның екінші заңы 21

2. 3 Күштер 25

2. 4 Механикалық күштер 26

2. 5 Ньютонның үшінші заңы (Ішкі күштер) 31

2. 6 Cалыстырмалық принцип. Галилей түрлендірулері 32

2. 7 Инерциалдық емес жүйелер (Инерциалдық күштер) 34

2. 8 Айналушы санақ жүйесі (Кориолис күші) 37

3 Импульстің сақталу заңы 39

3. 1 Механикалық жүйелер. Инерция центрі 39

3. 2 Импульстің сақталу заңы. Массасы айнымалы дененің қозғалысы 41

4 Энергия. Энергияның сақталу заңы 44

4. 1 Кинетикалық энергия. Жұмыс 44

4. 2 Потенциалдық энергия (консервативті күштер) 47

4. 3 Механикалық эенргияның сақталу заңы 50

4. 4 Энергияның сақталу заңына мысалдар 52

5 Айналушы дененің механикасы 56

5. 1 Күш моменті. Импульс моменті

5. 2 Айналушы дененің динамикасы

5. 3 Денелердің инерция моменттері 59

5. 4 Айналушы дененің энергиясы

5. 5 Импульс моментінің сақталу заңы

6 Тұтасқан ортаның механикасы

6. 1 Сұйық

6. 2 Бернулли теңдеуі 66

6. 3 Бернулли теңдеуінің салдары 68

6. 4 Сұйықтағы үйкеліс. Пуазейль формуласы 69

6. 5 Рейнольдс саны. Ұқсас ағыстар 72

6. 6 Денелердің сұйық (газ) ішіндегі қозғалысы. Стокс формуласы 74

7 Салыстырмалық теория элементтері 75

7 . 1 Эйнштейн постулаттары. Лоренц түрлендірулері 75

7. 2 Релятивистік қысқару 79

7. 3 Релятивистік жылдамдықтарды қосу 80

7. 4 Релятивистік динамика элементтері. Масса және энергия 82

Кіріспе

Физика - техниканың дамыуына, өркендеуіне күшті әсер ететін ілім. Сондықтан жастар физика негіздерін терең ұғынып, заңдарын үйреніп, тәжірибелік тәсілдерін меңгерулері тиіс. Сонда ғана техника мамандары бойынша жүретін пәндерді оңай меңгеретін болады.

Физиканы жете білмей келешекте техниканы дамыту, өндіріске жаңа тәсілдерді еңгізу мүмкін емес. Себебі физика техниканың негізін қалаушы ілімдердің бастысы.

Жалпы алғанда ғылыми анықтама бойынша физика - материяның жалпы қасиеттерін, қозғалыстарын зерттейтін іргелі ілім. Физика механикалық, жылулық қозғалыстардан бастап, электромагниттік, атомдық және ядролық құбылыстарды зерттейтін қанатын кең жайған ілім. Сондықтан да физиканың дамуы басқа ілімдердің өркендеуіне күшті әсер етеді.

Физика - техниканың іргетасын қалаушы білімнің бірі. Физика ілімінде ашылған әрбір заңдылық техниканың дәрежесін жаңа сатыға көтереді, өркендеп өсуіне әсерін тигізеді.

1 МЕХАНИКА

1. 1 Механикалық қозғалыс

Табиғатта кездесетін қозғалыстардың ең қарапайым түрі: механикалық қозғалыс . Денелер кеңістікттің белгілі бір бөлігінде орналасады. Денелер орын ауыстыра бастағанда олардың ара қашықтығы өзгереді. Дене басқа денелерге қарағанда орын ауыстырса біз оны қозғалады дейміз. Кейде дене тұтас алғанда бір орында тұрғанымен, оның жеке бөліктері қозғалады, мысалы; дене айналғанда оның әрбір бөлігі өзінше қозғалады. Ал денені қысқанда оның бөліктері бір - біріне жақындайды, демек, орын ауыстырады, яғни қозғалады. Қозғалыстың қай түрі болмасын ол салыстырымалы . Дененің не материалдың нүктенің қозғалғанын тек басқа денелермен салыстыру арқыл анықтаймыз. Жол бойын бақылағанда, оңды - солды өткен машиналарды қозғалмай тұрған бағанға қарап, ал вагон, автобус ішінде отырып орындықтарға, қабырғаға қарап адамдардық әрлі - берлі қозғалғанын, яғни орын ауыстырғанын бақылаймыз.

Жалпы алғанда табиғатта қозмалмайтын дене болмайды. Жер бетінде қозғалмай тұр дейтін денелердің өзі Жермен бірге Күн айналады. Күннің өзі әлем кеңістігінде, галактикалық жүйеде қозғалады.

Мысалы, машинаның қарапайым қозғалысын анықтау үшін бақылаушы өзі тұрған маңайдағы бір бағанды санақ денесі ретінде алып, ОХ өсін оңға қарай жол бойымен созады. (1сурет) Уақытты қол сағатымен өлшейді. Сонда машина (дене) тек ОХ өсінің бойымен түзу қозғалса, уақытқа байланысты тек Х өзгереді, демек x=x(t) . Бұл жағдайда z координатасы мен y координаталары өзгермейді.

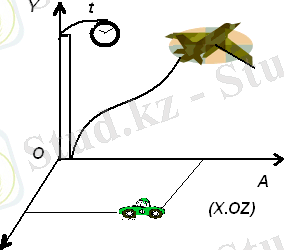
1-сурет

Түзу сызықты декарттық координаталардың өзі екі түрлі болуы мүмкін: оң жүйе деп аталатын түрінде О өсін бұранданың қозғалысымен бағыттас, шынында да оның сабын х - тен у - ке қарай бұрсақ өзегі жоғары жүретін болады. Ал теріс деп аталатын координаталық жүйеде ол төмен қарай қозғалады, ол О пунктирмен белгіленген. Бұл екеуін қалай айналдырсақта бірі - біріне келтірмейді. Оң жүйені сол жүйеге ауыстыру үшін өстердің бірін кері түрге айналдыру керекн. Координаталар жүйесінің таңбасына қарай қорытылатын формулалардың таңбалары да әр түрлі болады. Бірақ көпшлік жағдайда тек оң таңбалы координаталар жүйесі қолданылады, соны ұмытпауымыз керек. сондай дененің қозғалысын сипаттау үшін уақытқа тәуелді оның орын ауыстыруын, демек, координаталарын анықтай білу керек. Ең қарапайым қозғалыс ретінде механикада материалдық нүтенің кеңістіктегі орын ауыстыруы қарастырылады. Берілген жағдай денені материалдық нүкте деп қарастыруға болмайтын болса, онда оны ұсақ бөліктерге жіктеп, әр бөліктің жеке қозғалысы, сосын барлық бөлшектердің жиынтық қозғалысы қарастырылады. Мұнда белгілі бір көлемдегі бөлшектер не денелер жиынтығы жүйе деп аталады.

Механикалық қозғалысты зерттеу дегеніміз - берілген санақ жүйесін оның орын ауыстыру заңдылығын ашу. Қозғалыстың түрін толықғырақ сипаттау үшін ху координаталармен бірге радиус - векторын еңгізу қажет. Радиус - вектор материалдық нүктенің кеістіктегі орнын белгілеумен қатар, оның қозғалысын бағытын да көрсете алады. Радиус - векторының ұзындығын, яғни модулі және бағыттары (ОУ өстерімен жасайтын бұрыштары - 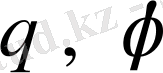) белгілі болса, онда х, у және z координаталарының мәндерін табу оңай. 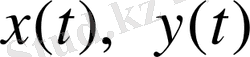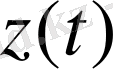Сондықтан да және қозғалыс теңдеулерінің орнына бір ғана 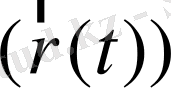векторлық теңдеуін жазуға болады.

Материалдық нүкте М ₁ - ге орын ауыстыру үшін кеңістікте көптеген нүктелерді (2-сурет) басып өтеді. Осы нүктелер арқылы жүргізілген сызықты траектория деп атайды. Траекторияның түріне қарай қозғалыс түзу сызықтық не қисық сызықты болуы мүмкңн.

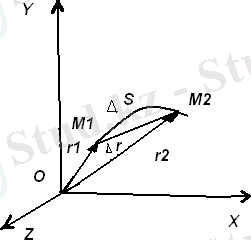
2-сурет

Екі нүктенің аралығындағы траекторияның ұзындығын 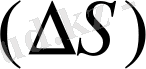көрсетілетін шаманы жүрілген жол деп атайды. Ал бастапқы М ₁ нүктесінен М ₂ қарай жүрілген векторлық шаманы орын ауыстыру векторы деп атайды.

2 - суреттен орын ауыстыру векторы радиус векторының өзгеруіне тең: 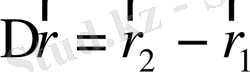. Орын ауыстыру векторының шекті мәні траекторияға жанама болады және бағыты қозғалыстың бағытын көрсетеді, ал модулі 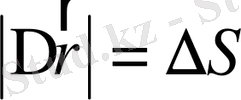. Сонымен, қорыта айтқанда, механиканың негізгі шешетін мәселесі: әрбір уақыт үшін дененің кеңістіктегі орнын, былайша айтқанда, координаталарын, яғни координаталардың ұзындығын, ара ғашықтығын табу.

Координаталарды өлшеу үшін ұзындық бірлігі метр (1м) қолданылады.

Дәл өлшеуді қажет ететін екінші бірлік уақыт, дәлірек айтқанда, уақыт аралығы. Себебі уақыт аралығы арқылы құбылыстың дамуын сипаттаймыз.

1. 2 Түзу сызықты қозғалыс

Табиғатта қозмалмайтын дене болмайды және қозғалыстың түрлері көп. Бір - бірімен әсерлесудің салдарынан денелердің орны, қозғалыстың түрлері үздіксіз өзгеріп отырады. Қозғалыстың себептерін іздестірмейміз, әуелі қозғалыстың кеңістіктегі түрлерін, оны сипаттайтын шамалар арасындағы байланысты анықтайық. Осы тұрғыдан қозғалыс заңдылықтарын қарастыратын механика бөлігін кинематика деп атайды.

Сонымен кинематиканың негізгі мақсаты, қозғалыстың түрлеріне қарай, қозғалыс теңдеулерін, яғни материалдық нүктенің координаталарын, өзгеру заңдылықтарын 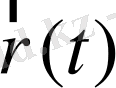анықтау. Жалпы алғанда дененің қозғалысын сипаттау деген сөз, оны құрайтын бөліктердің қозғалысын анықтау. Дененің бөліктері сыртқы әсерлердің салдарынан бір - біріне жақындамаса, не алыстамаса, дененің АВ аралығы өзгермесе, онда мұндай денені абсалют қатты дене дейді. Кеңістікте әрбір дененің орында тұрып дене айналса, оның әр бөлігі өзінше қозғалады.

Ал енді оның барлық бөліктері бірдей қозғалатын болса (АВ сызығы өзіне - өзі пареллель болса), (3-сурет) онда оны ілгерілемелі қозғалыс деп атайды. Мұндай жағдайда дененің қозғалысын сипаттау үшін бір ғана нүктенің, әдетте, ауырлық центрін белгілейтін нүктенің қозғалысын қарастырған жөн.

Әуелі материалдық нүктенің кинематикасын қарастырайық. Материалдық нүктенің қозғалысын анықтау үшін, біріншіден, оның кеңістіктегі орнын, координаталарын және және осы шамалардың уақытқа байланысты өзгеруін табу керек.

3- сурет 4-сурет

Математика тілімен айтқанда 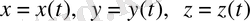сияқты кинематикалық теңдеулердің түрлерін анықтау. Координаталардың өзгеру заңдылықтары белгілі болса, онда траекторияның түрін, жүрілген жолды, орын ауыстыру векторын табу қиын емес.

Материалдық нүкте қысқа мерзім ішінде әр түрлі жол өтуі мүмкін. Демек, бірде тез, бірде ақырын жүруі ықтимал.

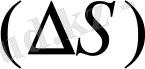Қозғалыстың тездігін сипттау үшін уақыт бірлігінде өтетеін жол арқылы өрнектелетін шама - жылдамдық еңг ізілген. Материалдық нүкте аралығында ж ол өтсе, оның жылдамдығы 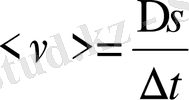болады, шынында бұл орташа жылдамдық.

Әрбір нүктедегі дененің жылдамдығын табу үшін жолдың кішкене бөлігін алу керек, сонда жылдамдықтың осы тұстағы шекті - дәл мәні шығады, демек,

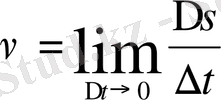не 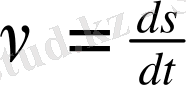(1. 1)

Бұл жерде біз туындының (дифференциалдың) физикалық мағынасы ашып отырмыз. 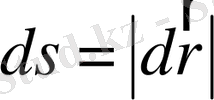, сондықтан 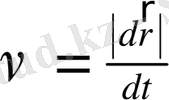. Осы шаманы векторлық түрде жазсақ

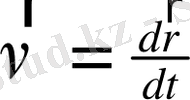(1. 2)

Орын ауыстыру векторы траекториясының бойынша жатыр, сондықтан да жылдамдықта векторлық шама болады. XYZ координата жүйесінде векторының орнына оның 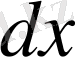, , 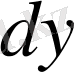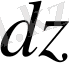проекцияларын алуға болады, ендеше 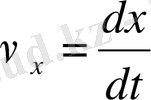, , 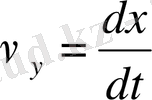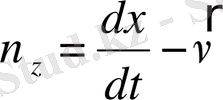векторының проекциялары шығады.

Егерде материалдық нүктенің жүген жолын есептеу қажет болса, онда (1. 1) формуласын пайдаланамыз. Мұнда , 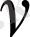- жылдамдық векторының модулі 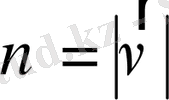. Ал 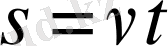деп жаза салуға болмайды, себебі жылдамдықтың өзі жол бойында өзгеруі мүмкін. Мысалы, оның уақыт аралығында жылдамдық өзгермейді десек, онда 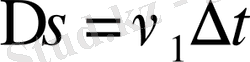деп жаза аламыз. Сол сияқты - ні табамыз. Барлық жүрілген жол

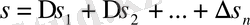Математикалық тұрғыдан осы жолдың дәл мәні интеграл арқылы табылады.

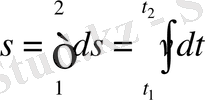
Бұл 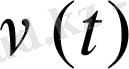функциясының мен 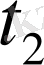аралығындағы аудан.

Материалдық нүкенің түзу сызық ьойымен бірқалыпты (ОХ - пен) қозғалысы кезіндегі оның кеңістіктегі орнын, демек, жүрген жолын табу оңай: . Мұнда Z=0, y=0, ал

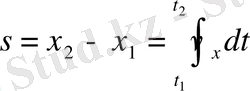
ендеше

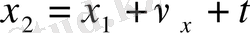Кейбір жағдайларда денелердің жылдамдығы тұрақты болмай, өзгеруі мүмкін. Мысалы, бір орыннан қозғала бастаған пойыздың жылдамдығы бірте - бірте артады, ал керісінше, тоқтағанда кемиді. Бастапқа 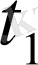уақытында оның жылдамдығы 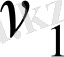болса, ал 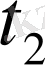уақытында 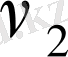болады. Жылдамдықтың өзгерісін сипаттайтын шама үдеу . Үдеу жылдамдықтың уақыт бірлігінде өзгеруін көрсететін шама. Оны “a” әрпімен белгілесек, түзу сызықты қозғалыста

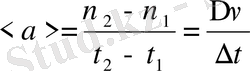не .

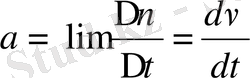Жылдамдықта үдеу векторлық шамалар:

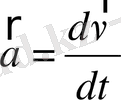не 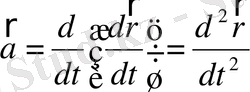. (1. 3)

Егерде қозғалыс түзу сызықты болса, онда үдеу векторы да жылдамдық векторы сияқты, орын ауыстыру векторының бойында жатады. Бірақ бағыты жағынан оған қарама - қарсы да болуы мүмкін, мысалы, дененің тежейтін болсақ, онда жылдамдық кемиді де үдеу таңбасы теріс болады. Жылдамдық векторы не оның өстерге проекциялары 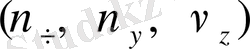белгілі болса, үдеудің де проекцияларын табу қиын емес.

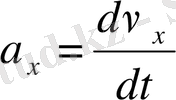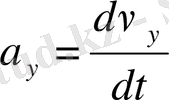, және .

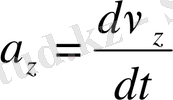Бұл шамаларды координаталар арқылы өрнектесек (x, y, z не ) 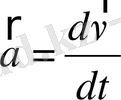, ал 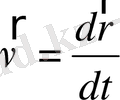десек,

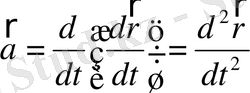(1. 4)

осы сияқты

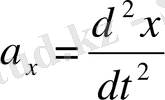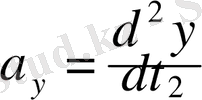, және .

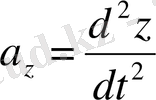Түзу сызық бойымен қозғалатын материалдық нүктенің үдеуі тұрақты болса, оны бірқалыпты үдемелі қозғалыс дейді.

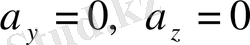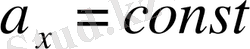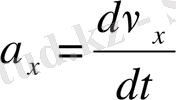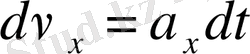Мұнда координата өстерінің біреуін (ОХ өсін) орын ауыстыру векторының бағыты өзгемейді, демек, , ал . Осы жағдайларды ескере отырып, қозғалыстың кинематикалық заңдарын жазайық: не әрі 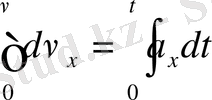интегралдау нәтижесінде: 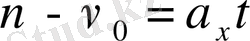, бұдан .

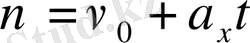Механиканың негізгі мақсаты t уақыт үшін координаталарын анықтау. Демек, үдеу арқылы х ₂ -ні табу. Жалпы алғанда

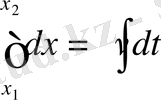Бірқалыпты үдемелі қозғалыс үшін

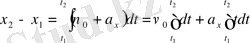сонымен

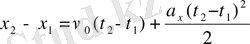бұдан .

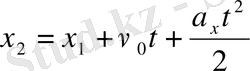1. 3 Қисық сызықты қозғалыс. Нормаль үдеу

Денелер көбінесе қисық сызықты траекториямен қозғалады. Материалдық нүкте қисық траекториямен қозғалғанда, жылдамдық векторының бағыты өзгеріп отырады, әрине, жылдамдықтың шамасы да өзгеруі мүмкін.

Қарастыруға ыңғаилы болу үшін материалдық нүкте санақ жүйесінің ХОУ жазықтығында қозғалады деп есептейік. 5 - суретте көрсетілген қозғалысты қарастырайық. уақыт ішінде дене кеңістіктің М ₁ нүктесінен М ₂ нүктесіне жетсін, ал жылдамдық - ден - ге өзгерсін, шама жағынан десек, бұл үдемелі қозғалыс, бірақ, мәселе тек мұнда ғана емес, өйткені векторы бағыты бойынша да өзгеріп отыр. Осы өзгерістің мағынасын түсіру үшін векторын векторының тұсына келтірейік, сонда оның шамасына өзгеретінін көреміз, енді оның өзі екі бөлікке жіктеуге болады:

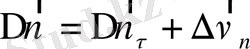
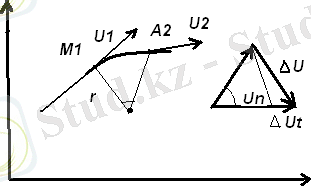
5-сурет.

Мұндағ 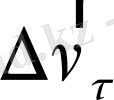- жылдамдықтың уақыт ішінде қаншалықты өзгеретінін көрсететін шама, оның уақытқа қатынасы, әдетте, үдеуді береді, шекті жағдайда ол траекторияға жанама болады, сондықтан да оны тангенциал үдеу деп атайды.

.

Жылдамдық векторының өзгеруін көрсететін екінші бөлігі жылдамдық векторының қаншалықты бұрылғанын, еңкейгені көрсетеді. Бұл шама да жылдамдықтың өзгеруін көрсетеді, бірақ нормаль бағыттағы үдеуді береді;

.

Сонымен бұл үдеу доғаның ішіне қарай радиус бойымен бағытталған нормаль үдеу аталады. Үдеудің модулін табу үшін 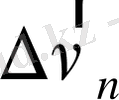векторының ұзындығын, модулін анықтайық: 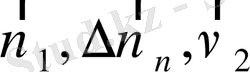векторлары мен 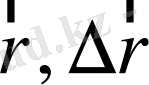сызықтары тұратын үшбұрыштар өзара ұқсас, сонда 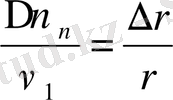не 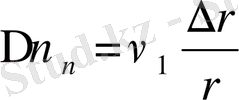, демек, 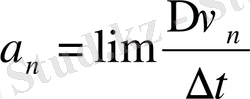. Бұдан 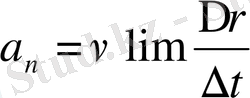, ал орын ауыстыру векторының модулі, шекті жағдайда 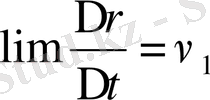, соның М ₁ нүктесі үшін 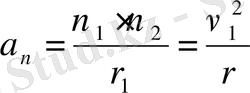, ал кез келеген нүкте үшін

(1. 5)

Радиусқа кері шамасын траекторияның қисықтығы (С) деп атайды. Шынында да доға көбірек иілсе, оның радиусы кішірейеді, яғни қисықтығы артады. Сонда нормаль үдеуді былай жазуға болады.

.

Былайша айтқанда, нормаль үдеуі траекторияның қисықтығын артқан сайын өседі. Нормаль үдеу де векторлық шама, ол әрқашанда радиустың бойымен центрге қарай бағытталған.

Қорыта келгенде материалдық нүкте қисық траекториямен қозғалса, оның екі түрлі үдеуі болуы мүмкін: біріншіден, нормаль, екіншіден, тангенциал үдеу. Толық үдеу осы екі вектордың қосындысына тең

,

модулі

.

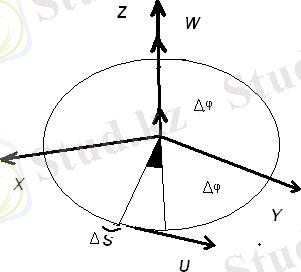
1. 4 Материалдық нүктенің шеңбер бойымен қозғалысы

Қисық сызықты қозғалыстың қарапайым түрі материалдық нүктенің шеңбер

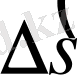бойымен қозғалуы. Мұнда кеңістіктегі траекторияның түрі өзгермейді. Материалдық нүкте ХОУ жазықтығында жатқан шеңбердің бойымен қозғалса, нүкте уақыт ішінде доғасын сызады, ал радиус - вектор 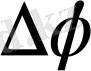- ға бұрылады.

Траектория (шеңбер) бойындағы жылдамдық 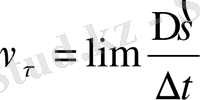. Бұрыштың радиандық өлшемі 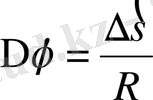не 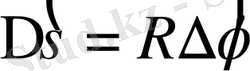, демек, 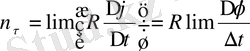. Соңғы шаманы бұрыштық жылдамдық деп атайды. Мұндағы 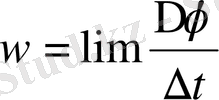. Сонымен

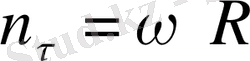. (1. 6)

Мұндағы бір ескере кететін жайт, бұрыштың өзгеруі 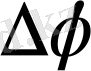- векторлық шама, себебі ол сағат тілінің бағыты бойымен де не оған қарсы даөзгеруі мүмкін. Сондықтан да 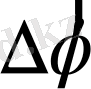векторының бағытын анықтау үшін бұранда ережесі қолданылады. Бұрандағы 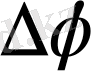- дің өсуі бағытында айналдырсақ, 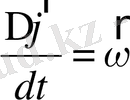векторының бағытын береді, ол шеңбер жазықтығына перпендикуляр болады (6-сурет) . Осыдан (1. 6) формуладағы шамалардың

( - дің) векторлар екенін еске алсақ, мынадай векторлар көбейтіндісі шығады

6-сурет.

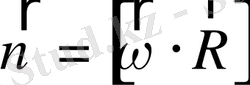. (1. 7)

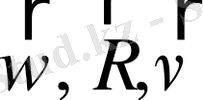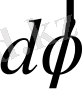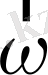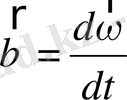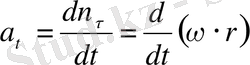Векторлық көбейтудің ережесі бойынша бұл үш вектор бір - біріне перпендикуляр болады, шынында да шеңберге жанама, оған перпендикуляр, бұл екеуіне , векторлары перпендикуляр. Бұрыштық жылдамдық уақыты байланысты өзгерсе, бұрыштық үдеу пайда болады. Айналу жазықтығы өзгермейтін нүкте үшін , ал не ,

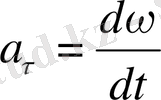сонымен

. (1. 8)

Материалдық нүкте шеңбер бойымен тұрақты бұрышты үдеумен қозғалады: 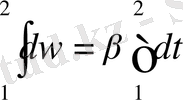, бұдан

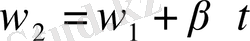
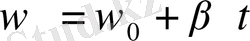, (1. 9)

сол сияқты айналу бұрышы үшін де, түзу сызықты қозғалыстағы сияқты, былай жаза аламыз

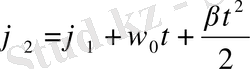. (1. 10)

1. 5 Еркіндік дәрежесі

Кеңістікте материалдық нктенің орнын анықтау үшін декарттық координаталар жүйесінде үш шаманың (x, y және z) мәндерін білу керек. Сол сияқты полярлық координаталар енгізсекте үш шаманың 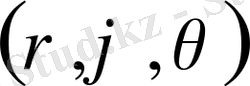мәндерін алу керек.

Материалдық нүктенің кеңістіктегі еркін қозғалысын сипаттайтын координаталарының санын еркіндік дәрежесі (i) деп атайды. Сонда материалдық нүкте i=3 тең.

Егерде материалдық нүкте біржақты байланысса, онда еркіндік дәрежесінің саны кемиді. Мысалы, жер бетінде қозғалатын денелер үшін тек х, у координаталары өзгереді де, z координатасы өзгермейді, себебі жердің тартуы (байланыс) оны еркін көтерілуге мүмкіндік бермейді. Сондықтан да біржақты байланысқан дененің дәрежесі кемиді: i=3-1=2.

Ал енді жер бетінде бір өске бекітілген денені алсақ, ол тек осы өсті айналады, еркіндік дәрежесінің саны i=1 тең болады. Шынында денені материалдық нүкте деп қарастырайық, онда оның орнын анықтау үшін тек бұрышын (бір ғана координатны) енгізсек жеткілікті. Себебі 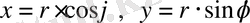. Мұнда тек бұрышы ғана өзгереді. Сонымен байланыстың саны артқан сайын дененің еркіндік дәрежесі кемиді.

Егерде кеңістікте бір немесе көптеген материалдық нүктелер болса, координаталардың жалпы саны артады (x ₁ , y ₁ , z ₁ ; x ₂ , y ₂ , z ₂ ; x ₃ , y ₃ , z ₃ ; …) . әдетте, мұны өрнектеу үшін жалпылама (q ₁ , q ₂ , q ₃ , …, q _i , …, q _n ) деп аталатын координаталар жүйесін енгізеді. Егерде нүтелердің арасында (k) байланысы туса, еркіндік дәрежесінің жалпы саны артады (i=N-k) .

Кез келген қатты денені алсақ, оның еркіндік жәрежесінің 6 - ға тең. Себебі оның кеңістіктегі орналасуын сипттау үшін x, y, z және 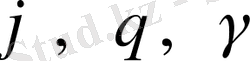координаталары керек. x _с , y _с , z _с координаталары дене центрінің ілгерілемелі қозғалысын сипаттаса, 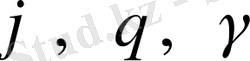дененің айналу құбылысын өрнектеу үшін 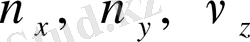, 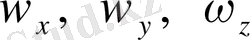сияқты жылдамдықтар енгізіледі.

2 ДИНАМИКА

2. 1 Ньютонның бірінші заңы

Табиғаттағы денелердің бәрі де бір - бірімен әсерлеседі, сөйтіп оның кеңістіктегі орны не түрі, жалпы алғанда күйі өзгереді. Күй деген сөздің физикалық мағынасы өте терең. Берілген жүйеде дене қозғалмауы мүмкін, біз оны тыныштық күйде түр дейміз.

Бірақ қозғалмай тұрған дене сығылуы, созылуы, не қызуы, тіпті жарық шығару мүмкін. Жалпы алғанда, дененің күйін сипаттайтын физикалық шамаларды параметрлер деп атайды. Қарапайым механикалық қозғалыстағы дененің күйін сипаттау үшін координаталар, жылдамдық, үдеу және күш сияқты параметрлерді білу қажет.

Дененің қозғалу есептерін себептерін, қозғалыс күйінің өзгеруін қарастыратын механика бөлімін динамика деп атайды.

Қозғалыстың қарапайым түрі - ілгерілемелі қозғалыс. Мұндай дененің барлық бөліктері бірдей қозғалады, бірдей үдеу алады, бірдей орын ауыстырады. Сондықтан да қатты дененің қозғалысын зерттеу үшін оның бойындағы бір нүктенің ғана қозғалысын алады.

Сонда дененің массасы осы нүктеде жинақталған материалдық нүкте деп қарастырылады. Бұдан ары осылайша алатын боламыз.

Көпшілік жағдайда біз Жерді қозғалмайтын жүйе деп есептеп, сол тұрғыдан басқа денелердің қозғалысын қарастырамыз. Бақылауымыз бойынша “бір жерде” тұрған дене өзінен - өзі қозғалмайды, демек, тыныштық күйін сақтайды. Бұл дене орнынан қозғалу үшін оған сырттан әсер ету керек. Ал енді орнынан қозғалып кеткен дене өзінің осы күйін сақтай ала ма? Былайша айтқанда, тұрақты жылдамдығы өзінен - өзі өзгере ме? Тәжірибеге жүгінсек қозғалып келе жатқан машина моторы өшкен бойда, баяулап тоқтайды.

Мұз айдында сырғанап бара жатқан дене де біраз жүріп барып, тоқтайды, себебі оған мұз, ауа бөгет жасайды. Демек, дененің тоқтауына себепші, әсер ететін екінші денелер. Ал енді қозғалушы денеге әсер ететін басқа денелер болмаса ше? Онда дене тұрақты жылдамдықпен қозғала береді де, қозғалыс күйін сақтар еді. Мұндай қорытындыны алғаш рет Г. Галилей айтқан болатын. Дегенмен де, динамика негіздерін үш түрлі заң ретінде 1687 ж. И. Ньютон тұжырымдаған болатын.

Ньютонның бірінші заңы бойынша: басқа денелер әсер етпесе, дене өзінің тыныштық күйін немесе түзу сызықты бірқалыпты қозғалыс күйін сақтайды. Сонымен дене тұрақты жылдамдықпен қозғалу үшін сырттан әсер етудің қажеті жоқ.

Қайта олардың болмағаны жөн. Ең дұрысы дененің еркін қозғалғаны. Жылдамдықтың сақталуы (қозғалыс күйінің сақталуы) материяның бәріне тән қасиет, оны инерттік деп айтады. Дененің еркін қозғалуын инерциалды қозғалыс деп атайды.

Ньютонның бірінші заңы дененің инерциалдық қасиетін сипаттайтын заң. Сондықтанда оны инерция заңы деп атайды. Денелер бір - біріне қатысты жылдамдықпен қозғалса, онда бұлардың бәрі де инерциялы қозғалушы денелер болады.

Сол сияқты бір - біріне қатысты тұрақты жылдамдықпен қозғалатын санақ жүйелері инерциялдық болады. Бұл жүйелердің бәріне де Ньютон заңдары орындалады. Сондықтан да Ньютон заңдары орындалатын санақ жүйелерін инерциялдық деп атайды.

Кеңістікте дененің қозғалуын зерттеу үшін инерциялдық жүйелердің бірін алу керек. Осы жүйемен салыстыра отырып дененің жылдамдығын, үдеуін, траекториясын, яғни жалпы күйін анықтай аламыз.

2. 2 Ньютонның екінші заңы

Ньютонның екінші заңы бойынша қозғалыс күйінің өзгеру себептерін қарастырады. Кез келген дененің күйін өзгеру үшін оған басқа денелер әсер етуі керек. Мысалы, үстел үстінде тыныш жатқан шарды итерсек ол қозғалып, үдеу алады. Сол сияқты қозғалып келе жатқан денені тоқтату үшін сырттан әсер ету керек, сонда ол кері бағытталған үдеу алады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.