Матрицалар және сызықты теңдеулер жүйелері: теория және есептеу әдістері


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 50 бет
Таңдаулыға:
Мазмұны
Кіріспе
Бірінші тарау
Матрицалар туралы негізгі ұғымдар және түсініктер
1. 1 Негізгі анықтамалар және мысалдар . . .
1. 2 Матрицаларға амалдар қолдану . . .
1. 2. 1. Матрицалар теңдігі . . .
1. 2. 2 Матрицаларды қосу . . .
1. 2. 3 Матрицаларды санға көбейту . . .
1. 2. 4 Матрицаларды көбейту . . .
1. 2. 5 Матрицаны транспонирлеу . . .
1. 3 Матрицалар алгебрасының маңызы
және рөлі туралы . . .
1. 4 Матрица рангі туралы . . .
1. 5 Матрицаның жатық жолдарына
жүргізілетін элементар түрлендірулер . . .
1. 6 Матрицаны сатылы түрге келтіру
және оның матрица рангімен байланысы . . .
Екінші тарау
Сызықты теңдеулер жүйесі және матрица
2. 1 Негізгі ұғымдар және анықтамалар . . .
2. 2 Біртектес теңдеулер жүйесі . . .
2. 2. 1 Негізгі қасиеттері . . .
2. 2. 2 Жүйенің жалпы шешімі . . .
2. 2. 3 Гаусс әдісі туралы . . .
2. 2. 3. 1 Есте болатын бір жағдай . . .
2. 3 Біртектес емес теңдеулер жүйесі . . .
2. 3. 1 Жүйе шешімдерінің негізгі қасиеттері . . .
2. 3. 2 Біртектес емес теңдеулер жүйесінің
үйлесімділік критерийі . . .
Үшінші тарау
Матрицаның анықтауыштары туралы
3. 1 Екінші және үшінші ретті анықтауыштар . . .
3. 2 Анықтауышты жатық жол бойынша жіктеу . . .
3. 3 Анықтауыштардың негізгі қасиеттері . . .
3. 4 Негізгі ескертулер . . .
Төртінші тарау
Кері матрица және оны есептеу туралы
4. 1 Кері матрица ұғымы . . .
4. 2 Кері матрицаны есептеу ережесі . . .
4. 3 Кері матрицаны есептеуде Гаусс әдісін
пайдалану туралы . . .
4. 4 Біртектес емес теңдеулер жүйесін шешуде
кері матрицаны пайдалану идеясы . . .
Бесінші тарау
Есептер шығаруға мысалдар
5. 1 Матрицаларға амалдар қолдану . . .
5. 2 Матрицаны сатылы түрге келтіру және
оның рангісін анықтау . . .
5. 3 Сызықты теңдеулер жүйесін шешу . . .
5. 3. 1 Біртектес теңдеулер жүйесін шешу ерекшелігі . . .
5. 3. 2 Біртектес емес теңдеулер жүйесін шешудегі ерекшелік . . .
5. 4 Жатық жол (немесе тік жол/баған) бойынша
жіктеу арқылы анықтауыштарды есептеу . . .
5. 5 Анықтауыштарды есептеуде Гаусс
әдісін пайдалану . . .
5. 6 Кері матрицаны табу . . .
Алтыншы тарау
Біліктілікті бекіту алгоритмдері
6. 1 Негізгі тақырыптар бойынша
біліктілік алгоритмдері . . .
6. 2 Негізгі тақырыптар бойынша
біліктілік тренингтеріне мысалдар . . .
6. 3 Өзіндік жұмысқа тапсырмалар . . .
6. 4 Глоссарий . . .
Қорытынды . . .
Пайдаланылған әдебиеттер . . .
Кіріспе
Математика ғылымының барлық салаларында, оның ішінде, әсіресе, экономикалық есептерді шешуде және келешек математикалық ғылыми зерттеулерде ең жиі қолданылатын математикалық аппаратқа сызықты алгебра элементтері жатады. Ұсынылып отырған оқу құралы оқырманның (студенттің, жас маманның) сызықты алгебра элементтерін өз беттерінше тиімді оқып-үйренуіне және оның негізгі жиі кездесетін қолданбалы әдістерін және тәсілдерін сапалы меңгеруіне арналады.
Матрицалар алгебрасының математиканың өзінің ішкі дамуындағы рөлі де бүгінгі күні жоғарыламаса әлі де төмендей қойған жоқ. Матрицалар теориясы әлі де даму үстінде. Өйткені, жылдан жылға оларды пайдаланудың әртүрлі бағыттары және түрлері көбейе және кеңи түсуде. Сондықтан американдық математик Ричард Беллман матрицалар теориясын «жоғары математиканың арифметикасы» деп бекер атамаған.
Жалпы математиканың даму тарихына көз жүгіртсек мына жағдайларды байқауға болады. Матрица туралы мәселе алғашқы рет ХІХ ғасырдың екінші жартысынан бастап ирландық астраном және математик У. Гамильтонның ( . . . ) және ағылшын математиктері Дж. Силвестрдің ( . . . ), А. Кэлидің еңбектерінде кездесе бастайды. Ал матрицалар теориясының негізін ХІХ ғасырдың екінші жартысында неміс математиктері К. Вейерштрасс (1815-1897) және Фробениус қалаған. Тарих тілінде айтсақ, матрицалар теориясы математиканың «жас» бағыттарының қатарына жатады. Сол себептен математиканың бұл бағыты әлі де даму кезеңінде. Өйткені, жылдан жылға матрица аппаратын пайдаланатын есептер аумағы көбейе түсуде.
Бұл оқ-әдістемелік құралының мақсаты - матрицаларға амалдар қолдануды, анықтауыштар мәселелерін қарастыру, нәтижесінде сызықты теңдеулер жүйесін зерттеу, яғни олардың шешімдерінің бар және жалғыз ғана болатындығын және оларды табудың әдістері (тәсілдері) туралы мәселелер ауқымын анықтау.
Қазіргі кезеңде математикалық әдістердің барлық дерлік ғылым, техника, экономика салаларында және барлық дерлік мамандардың практикалық қызметтерінде кеңінен қолданыс табуына байланысты математикалық білімді және дайындықты сапалы жақсарту мәселесі күн тәртібінен түспек емес, оның өзектілігі күннен-күнге күшейе түсуде. Оның ішінде, әсіресе, қарапайым және солғұрлым маңызды болып келетін сызықты алгебраның әдістерін және тәсілдерін меңгеру бірінші кезекте қажет болып тұр. Оқу құралы осы жағдайды ескеріп дайындалынып отыр.
Оқу құралында мына бастапқы мәселелерге баса назар аударылған: матрицалар туралы негізгі ұғымдар және түсініктер, матрица рангі туралы, матрицаның жатық жолдарына жүргізілетін элементар түрлендірулер, матрицаны сатылы түрге келтіру және оның матрица рангімен байланысы, с ызықты теңдеулер жүйесі және матрица, матрицаның анықтауыштары туралы, кері матрица және оны есептеу туралы, матрица аппаратын пайдаланып есептер шығару мәселелері.
Оқу құралы бірінші кезекте көптеген мамандықтар студенттеріне, магистранттарға және жас оқытушыларға ұсынылады. Оқу құралын әдістемелік құрал ретінде де пайдалануға болады деп ойлаймыз.
Бірінші тарау
Матрицалар туралы негізгі ұғымдар және түсініктер
1. 1 Негізгі анықтамалар және мысалдар
М атематикада матрица (немісше matrіse , латынша matrіx - аналық деген мағынада) деп кез келген нақты элементтер жиынынан құрылған және m жол (немесе жатық жол) мен n бағаннан (немесе тік жолдан) тұратын тік төртбұрышты А кестесін айтады.
Жалпы түрде матрицаны былайша жазады:
А=
 Equation. 3 .
Equation. 3 .
Немесе матрицаны қысқаша былай да белгілейді: А=(а іj ) mn, мұндағы i =1, 2, …, m; j =1, 2, …, n.
Матрицаны түзетін (құрайтын) нысандар оның элементтері деп аталады. Матрицаның элементтері оның жатық жолдары немесе бағаналарының (тік жолдардың) бойымен орналасады. Матрицаның элементтері а іj түрінде қос индекспен өрнектеледі, мұндағы бірінші индекс і - матрицаның а іj элементі орналасқан жатық жолының нөмірін , екінші индекс j - оның а іj элементі орналасқан бағананың нөмірін көрсетеді. Матрица символдық түрде не дөңгелек жақша , не қос тік сызық арқылы өрнектеледі. Мұндай матрицаны ( m, n ) өлшемді тікбұрышты матрица деп, ал егер m=n болса, квадрат матрица (n санын оның реті) деп атайды.
Мысалы, В=
Жатық жолдарының саны мен бағаналары санының бірі немесе екеуі де шексіз болатын матрицаны шексіз матрица деп түсінеміз. Бір ғана жатық жолдан немесе бір ғана бағанадан тұратын матрицалар да болады, яғни тікбұрышты матрицаның дербес жағдайлары вектор-жол немесе вектор-баған түрінде болуы мүмкін. Мысалы, С 14 =(0, 1, 1, -3) түріндегі матрицаны төртөлшемді вектор (0, 1, 1, -3) деп, ал D 51 =
а іі диагоналды элементтері ғана нөльден өзгеше болатын квадрат матрицаны диагоналдық матрица деп атайды, dіag(а 11 … а nn ) таңбасымен белгілейді.
Диагоналдық матрицаның барлық элементтері (а іi =1) болса, онда ол бірлік матрица деп аталады. Бірлік матрицаны былайша жазады:
Е=
Матрицалық есептеулерде бірлік матрицаның рөлі ерекше болып келеді. Ол туралы келесі беттерде айтатын және мысалдар келтіретін боламыз.
Сонымен, егер квадраттық матрицаның диагоналдық элементтерінің барлығы бірге тең, ал қалған элементтері нөльге тең болса, онда мұндай матрицаны бірлік матрица деп атаймыз.
Егер барлық (а іi =а) болса, онда скаляр матрица шығады.
Барлық элементтері нөльге тең матрица нөльдік матрица деп аталады. Бірлік және нөльдік матрицалар матрицалық есептеулерде сандардағы 1 және 0 сандары сыяқты рөльдерді орындайды.
Жатық жолдары мен бағаналарын ауыстыру арқылы алынған матрицаны
транспонирленген матрица
деп атайды, оны
А
немесе
А
Т
арқылы белгілейді. Егер матрицаның элементтерін комплекс түйіндеске ауыстырсақ, онда
комплексті түйіндес матрицасы
шығады. Ал егер А транспонирленген матрица элементтерін комплексті түйіндеске ауыстырсақ, онда
А
матрицасымен түйіндес болатын А* матрицасы шығады.
Квадрат матрицаның
анықтауышы A
немесе
det A
деп белгіленеді. Квадратты матрица
үшбұрышты
деп аталады, егерде бас диагоналдан төмен (немесе жоғары) орналасқан барлық элементтер нөльге тең болатын болса. Мысалы,
В=
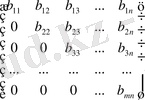
матрицасы жоғарғы үшбұрышты, ал
С=
түріндегі матрицаны төменгі үшбұрышты матрица деп атайды.
1. 2 Матрицаларға амалдар қолдану
Матрицаларға қосу, азайту, көбейту және санды матрицаға көбейту амалдары орындалады. Бірақ осы аталған амалдар кез келген матрицалар үшін орындалмайды. Сондықтан матрицалармен жұмыс істеген кездері осы жағдайды үнемі назарда ұстауымыз керек болады.
1. 2. 1 Матрицалардың теңдігі
Бірдей ретті екі матрица A mn = B mn тең деп аталады, егер екі матрицадағы индекстері бірдей барлық элементтер өзара тең болса ғана. Мысалы, егер
В=
онда b 11 = а 11 =-1, b 12 =а 12 =0, b 13 =а 13 =1, b 21 =а 21 =b 22 =а 22 =b 23 =а 23 =5.
1. 2. 2 Матрицаларды қосу
Матрицаға қосу, көбейту сыяқты алгебралық амалдар қолданылады.
Бірдей ретті екі матрицаны қосу деп, сол типтес, элементтері сәйкес екі матрицаның (қосылғыштардың) элементтерінің қосындысы болып келетін
A mn + B mn = C mn матрицасын айтады, яғни с ij =a ij +b ij , i=1, 2, …, m; j=1, 2, …, n.
Мысалы, егер
А
23
=
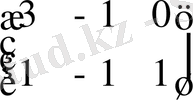 , В
23
=
, В
23
=
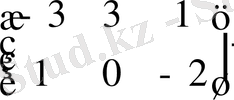
болса, онда олардың қосындысы тең болады
С 23 =А+В=
Есте болуы керек, егер О нөльдік матрица болса, онда А+О=О+А=А (мұнда нөльдік матрицаның реті А матрицасы ретімен бірдей болуы тиіс) .
Матрицаларды қосу амалының қасиеттерін атап кетейік:
А+В =В+А (қосудың коммутативтілігі) ;
(А+В) +С=А+(В+С) (қосу амалының ассоциативтілігі) .
1. 2. 3 Матрицаны санға көбейту
А mn тікбұрышты матрицасының
Мысалы,
-6Е=
 , яғни мұндағы
, яғни мұндағы
ал В=
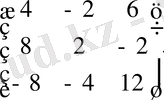 матрицасында 2 санын матрица таңбасының алдына шығаруға болады:
матрицасында 2 санын матрица таңбасының алдына шығаруға болады:
В =2
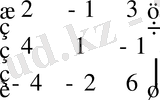 ,
,
бұл мысалда
Матрицаны санға көбейту амалының қасиеттерін атап кетейік:
Егер
(
Мына жағдайды атап кетуіміз керек: жоғарыдағы енгізілген амалдар бірдей ретті матрицаларға ғана қолданылады. Мысалы, С=А-В матрицасын алу үшін А матрицасының сәйкес элементтерінен В матрицасының сәйкес элементтерін алу керек болады.
А=
А -
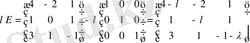 .
.
1. 2. 4 Матрицаларды көбейту
Матрицаларды бір-біріне көбейту амалын іске асыру, жоғарыдағы амалдармен салыстырғанда күрделі ережелерді орындау арқылы іске асырылады.
Бір матрицаны екінші матрицаға көбейту амалы 1-көбейткіш (бірінші матрица) бағаналарының саны 2-көбейткіш (екінші матрицаның) жатық жолдарының санына тең тік бұрышты матрицалар үшін ғана орындалады.
(m, p) өлшемді А матрицасының (p, n) өлшемді В матрицасына көбейтіндісінің элементтері с іj =а і1 b 1j +а і2 b 2j + +…+а іp b pj , і=1, …, m, j=1, …, n болатын (m, n) өлшемді C матрицасы болып табылады. Мысалы,
А 23 =
В
33
=
 матрицасына
матрицасына
көбейтуге болады. Көбейтіндінің (С - ның) размері (реті, өлшемі) 2х3 болады.
Енді, матрицаларды көбейтудің С=А
(a i1 a i2 … a in ) ;
Бөліп алған жатық жолмен және бөліп алған бағанның ұзындықтары (элементтер саны) бірдей болуы тиіс. Бөліп алған векторлардың бірдей орында тұрған элементтерін қос-қостан көбейтеміз және оларды қосамыз (яғни, осы векторлардың скалярлық көбейтіндісін есептейміз) . Алынған қосындыны с ij деп белгілейміз және оны C матрицасының і-жолы мен j- бағанының қиылысуындағы элементі деп қабылдаймыз:
с іj =а і1 b 1j +а і2 b 2j + +…+а іn b nj
Осы амалды А матрицасының әрбір жолымен және В матрицасының әрбір бағанымен орындай отырып, С матрицасы-көбейтіндінің элементтерін толтырамыз.
Мысалы:
С=
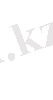
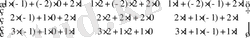
Егер элементі
Мысал келтірейік.
Жоғарыдағы А 23 матрицасын В 33 матрицасына көбейтейік:
Келтірген ереже бойынша А матрицасының бірінші жатық жолы - (1 -1 2), В матрицасының 1-ші бағаны -
с 13 элементі с 13 =1
Тура осылайша А матрицасының 2-ші жатық жолы - (0 1 1) мен В матрицасының 1-ші бағаны -
С=
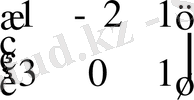 .
.
Матрицаларды көбейту ассоциативтілік қасиетіне (АВ) С=А(ВС) бағынады.
Бұл жерде мына жағдайға баса назар аударамыз: жалпы, сандарды көбейтумен салыстырғанда матрицаларды көбейту нәтижесі көбейткіштердің орналасу ретіне байланысты болады. Сонымен, матрицаларды көбейтуде көбейткіштердің орнын ауыстыру қасиеті орын алмайды (матрицаларды көбейту амалы коммутативті емес) .
Бұл деген сөз АВ=ВА орындалмай қалуы да мүмкін. АВ және ВА матрицаларының көбейтіндісі бірінші ретті квадрат матрица үшін ғана анықталады және көбейткіштердің ретіне де байланысты, яғни егер АВ=ВА болса, онда А және В матрицалары ауыспалы деп аталады. Мысалы, жоғарыдағы мысалда АВ анықталған, ал ВА анықталмаған, өйткені, В матрицасының бағандар саны А матрицасының жатық жолдарына тең емес.
Ал егерде А және В - бірдей өлшемді квадрат матрицалар болса, онда АВ және ВА көбейтінділерінің екеуі де бар болады, бірақта АВ= ВА болуы міндетті емес.
Мысалы, А =
АВ=
Матрицаларды көбейтуде Е бірлік матрицасы ерекше орын алады, ол сандарды көбейту кезіндегі 1 санының рөлін орындайды. Егер х бір сан болса, онда х
Біз білеміз, сандардың көбейтіндісі 0-ге тең болады тек сонда ғана, егерде көбейткіштердің бірі 0-ге тең болатын болса. Ал матрица жағдайында -
әрбір көбейткіші нөльден өзгеше болса да, екі матрицаның көбейтіндісі нөльдік матрицаға тең болуы әбден мүмкін.
Мысалы, А=
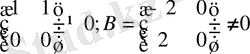 . Ал бірақта АВ=
. Ал бірақта АВ=
Екі квадрат матрицаның көбейтіндісінің анықтауышы көбейтілетін матрицалар анықтауышының көбейтіндісіне тең. Егер анықтауышы нөльге тең болмаса , онда А=(а іj ) квадрат матрицасы өзгеше емес деп, ал кері жағдайда ерекше матрица деп аталады. Кез келген өзгеше емес матрицаның АА -1 =Е теңдеуімен анықталатын бір ғана кері А -1 матрицасы болады. Бірдей n-ретті А және В квадраттық матрицалары ұқсас матрицалар деп аталады.
1. 2. 5 Матрицаны транспонирлеу
mxn ретті A mn матрицасы берілсін. Осы матрицада жатық жолдар мен бағандар орындарын ауыстырайық, яғни 1-жатық жолдың орнына 1-бағанды, 2-жатық жолдың орнына 2-бағанды және т. с. с. Алынған жаңа матрицаны А Т деп белгілейміз.
Сонымен,
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz