Шектеусіз үздіксіз бөлшектердің қолданылуы
ҚАЗАҚСТАН РЕСПУБЛИКАСЫ ҒЫЛЫМ ЖӘНЕ БІЛІМ МИНИСТРЛІГІ
МАТЕМАТИКА, ФИЗИКА ЖӘНЕ ТЕХНОЛОГИЯЛАР ФАКУЛЬТЕТІ
Математика кафедрасы
ДИПЛОМ ЖҰМЫСЫ
Тақырыбы: ШЕКТЕУСІЗ ҮЗДІКСІЗ БӨЛШЕКТЕРДІҢ ҚОЛДАНЫЛУЫ
МАЗМҰНЫ
КІРІСПЕ 3
1 ШЕКТЕУСІЗ ҮЗДІКСІЗ БӨЛШЕКТЕР 5
1. 1 Шектеусіз үздіксіз бөлшекке жіктеу 5
1. 2 Шектеусіз үздіксіз бөлшектің лайықты бөлшектері 14
1. 3 Лайықты бөлшектердің қасиеттері 16
1. 4 Квадрат иррационалдық және периодты үздіксіз бөлшектер 36
2 ШЕКТЕУСІЗ ҮЗДІКСІЗ БӨЛШЕКТЕРДІ ҚОЛДАНЫП
ЕСЕПТЕРДІ (ТЕҢДЕУЛЕРДІ) ШЕШУ 54
2. 1 Анықталмаған (бірінші дәрежелі) теңдеулер, оларды шешу 54
2. 2 Квадрат теңдеулер және оларды шешу 60
2. 3 Пелль теңдеулері. Пелль теңдеулерін шешу 64
ҚОРЫТЫНДЫ 77
ӘДЕБИЕТТЕР ТІЗІМІ 78
КІРІСПЕ
Сандар теориясы курсында үздіксіз бөлшектер теориясының маңызы зор. Басқа әдістер арқылы мұндай шешімдердің бар екені дәлелденіп жатқан кезде үздіксіз бөлшектерді қолдана отырып есептердің дәл шешімдерін беруге болады.
Үздіксіз бөлшектердің таза практикалық қолданылуымен қатар теориялық маңызы да зор. Олардың әдістері негізінен алғанда сандар теориясында, алгебрада, ықтималдықтар теориясында, тіпті, анализ бен механикада да қолданылады.
Үздіксіз бөлшектер жайлы біраз деректерге тоқталатын болсам, үздіксіз бөлшектер туралы деректер ХVІ ғасырдағы итальян математигі Р. Бомбеллидің еңбектерінде кездеседі. Оны ХVІІ ғасырда ағылшын математигі Дж. Валлис зерттеген. Үздіксіз бөлшектердің кейбір маңызды қасиеттерін Х. Гюйгенс ашқан. Сонымен қатар ХVІІІ ғасырда үздіксіз бөлшектер теориясының дамуына Л. Эйлер өзінің үлкен үлесін қосты. Ал П. Л. Марков пен А. А. Чебышев ХІХ ғасырда үздіксіз бөлшектерді ортогональ көпмүшеліктерді зерттеу үшін қолданды.
Сонымен қатар сандар теориясы пәнінің дамуында ұлы француз математигі Жозе Луи Лагранж, Эварист Галуа еңбектерінің мәні зор. Сандар теориясында Лагранж шектеусіз үздіксіз бөлшектер теориясының негізгі теорияларын берді және олардың анықталмаған теңдеулерді шешуге қолданылуын көрсетті. Сонымен қатар Лагранждың сандар теориясынан зерттеулері, нақты сандардың арифметикалық қасиеттерін оқып-білуде үздіксіз бөлшектердің негізгі рөл атқаратындығын көрсетті.
Э. Галуа теоремасының дәлелдеуі 1828 жылы жарыққа шықты. Сонымен қатар Галуа таза периодты жіктелуде түйіндес квадрат иррационалдықтың дәл сондай элементтері болады, бірақ ол элементтер кері тәртіппен орналасатынын дәлелдеді.
Жұмысымның мақсаты: үздіксіз бөлшектер, соның ішінде шектеусіз үздіксіз бөлшектердің теориялық маңызымен қатар практикалық қолданылуын
көрсету.
Диплом жұмысым мазмұн, кіріспе, екі тарау, қорытынды және әдебиеттер тізімінен тұрады. Бірінші тарауда рационал және иррационал санның үздіксіз бөлшекке жіктелуі, үздіксіз бөлшектердің лайықты бөлшектері, лайықты бөлшектердің қасиеттерін қарастырдым.
Екінші тарауда шектеусіз үздіксіз бөлшектердің практикалық маңызын, яғни қолданылу жақтарын ашып көрсеттім. Мұнда шектеусіз үздіксіз бөлшектерді қолданып анықталмаған теңдеулерді, квадрат теңдеулерді және Пелль теңдеулерін түрлі әдістермен шешуге болатынын, яғни шектеусіз үздіксіз бөлшектердің қолданылу аймағы өте кең екенін көрсеттім.
Диплом жұмысымның көлемі 78 бет.
1 ШЕКТЕУСІЗ ҮЗДІКСІЗ БӨЛШЕКТЕР
1. 1 Шектеусіз үздіксіз бөлшекке жіктеу
Үздіксіз бөлшектер кез келген заттық санды кез келген алдын ала берілген дәлдікпен рационал бөлшектер арқылы өрнектеуге мүмкіндік тудырады, бұл жағынан алғанда үздіксіз бөлшектердің маңызы ондық бөлшектердікінен кем түспейді.
\[a_{0}+{\cfrac{1}{a_{1}+{\cfrac{1}{a_{2}+{\cfrac{1}{a_{3}+K}}}}}}\]
(1)
түріндегі өрнекті үздіксіз бөлшек дейді. Мұндағы
\[a_{0},a_{1},a_{2},a_{3},\mathrm{K}\]
сандары,
\[~{\mathcal{Q}}_{0}\]
-ден басқасы, бүтін оң сандар. Олар үздіксіз бөлшектің толымсыз бөлінділері деп аталады. Шектеулі толымсыз
\[a_{0},a_{1},\ K\;,a_{n}\]
бөлінділері бар үздіксіз бөлшекті шектеулі, ал шектеусіз толымсыз
\[a_{0},a_{1},K\]
бөлінділері бар үздіксіз бөлшекті - шектеусіз үздіксіз бөлшек деп атайды. Егерде толымсыз бөлінділердің мәндері мен орналасу реті берілсе, онда үздіксіз бөлшек толық анықталған деп саналады. Сондықтан
\[a_{0},a_{1},a_{2},a_{3},\mathrm{K}\]
толымсыз бөлінділі үздіксіз бөлшекті
деп те белгілейді. Олай болса,
\[\left[a_{0},a_{1},a_{2},a_{3},\mathrm{K}\right]=a_{0}+{\cfrac{1}{a_{1}+{\cfrac{1}{a_{2}+{\cfrac{1}{a_{3}+\mathrm{K}}}}}}}\]
Теорема. Кез келген рационал санды шектеулі, ал иррационал санды шектеусіз үздіксіз бөлшек түрінде көрсетуге болады.
Дәлелдеуі. Шынында да, айталық
\[{\mathcal{Q}}\]
рационал сан болсын,
\[\alpha={\frac{\alpha}{b}}\]
.
\[{\mathcal Q}\,\]
-ны
\[\mathit{\mathcal{I}}\]
-ге бөліп,
\[a\,=b a_{0}+r_{0},\]
0<
\[{\mathcal{J}}_{0}^{*}\]
<
\[\mathit{\mathcal{I}}\]
, (2)
екенін табамыз. Мұндағы
\[~{\mathcal{Q}}_{0}\]
саны
\[\frac{Q}{J}\]
-ден аспайтын ең үлкен бүтін сан, яғни
\[a_{0}={\frac{\hat{\mathrm{e}}a\,\hat{\mathrm{e}}}{\hat{\mathrm{g}}}}\,\bigg|_{1}\]
екені түсінікті.
(2) теңдікті
түрінде қайта жазып,
\[\mathit{\mathcal{I}}\]
-ні
\[{\mathcal{J}}_{0}^{*}\]
-ге бөлеміз:
\[b=r_{0}a_{1}+r_{1},\]
\[0\leq r_{i}\]
<
\[{\mathcal{I}}_{0}^{*}\]
, (4)
мұндағы
\[Q_{1}\]
саны
\[\frac{\partial}{r_{0}}\]
-ден аспайтын ең үлкен бүтін сан болады, яғни
\[a_{1}={\frac{\hat{\mathrm{e}}b^{\frac{n}{6}}b^{\frac{1}{n}}}{\hat{\mathrm{e}}}}\]
.
(4) -ден
\[\frac{b}{r_{0}}=a_{1}+\frac{1}{\frac{\Im}{\Lambda r_{0}}\frac{\vartheta}{\Lambda}}{\Lambda}\bigg.\]
мәнін тауып, (3) -ге қоямыз. Сонда
\[\frac{a}{b}=a_{0}+\frac{1}{a_{1}+\frac{1}{3r_{0}}\frac{\vartheta}{\vartheta}}{\vartheta}_{\star}\]
(5)
Енді
\[{\mathcal{J}}_{0}^{*}\]
-ді
\[{\mathcal{Y}}_{1}^{*}\]
-ге бөлеміз:
\[r_{0}=r_{1}a_{2}+r_{2}\,,\quad0\ \leq r_{2}\]
<
\[{\mathcal{Y}}_{1}^{*}\]
,
мұндағы
\[a_{2}={\frac{6r_{0}}{\mathrm{e}^{2}+\mathrm{i}}}.\]
Бұдан
\[\frac{r_{0}}{r_{1}}\]
-нің мәнін
\[\frac{r_{0}}{r_{1}}=a_{2}+\frac{1}{\frac{\mathrm{d}r_{1}\;{\dot{\mathbb{Q}}}}{\mathrm{d}r_{0}}}.\]
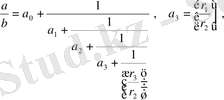
тауып, (5) -ге қойсақ, мынау шығады:
\[{\frac{a}{b}}=a_{0}+{\frac{1}{a_{1}+{\frac{1}{a_{2}+{\frac{1}{\frac{1}{\Delta r_{1}}}}}}}{\frac{\Lambda}{\Lambda r_{0}}}};\]
(6)
Тағыда
\[{\mathcal{Y}}_{1}^{*}\]
-ді
\[\textstyle{J}_{2}^{*}\]
-ге бөлеміз:
\[r_{1}=r_{2}a_{3}+r_{3}\,,\quad0\ \leq r_{3}\]
<
\[\,T_{2}.\]
аламыз.
Бұдан әрі
\[\frac{r_{2}}{r_{3}}\]
қатынасын тауып,
\[r_{2}=r_{3}a_{4}+r_{4}\,,\quad0\ \leq r_{4}\]
<
\[{\boldsymbol{r}}_{\boldsymbol{3}}\,,\]
\[\frac{r_{2}}{r_{3}}=a_{4}+\frac{1}{\frac{\mathrm{d}r_{3}\,\mathrm{d}}{\mathrm{d}r_{4}}}{\bigg)}.\]
жоғарыдағы сияқты, (7) -ге қоямыз және осы процесті соза береміз. Мына
теңдіктері мен
\[\mathit{\mathcal{I}}\]
>
\[{\mathcal{J}}_{0}^{*}\]
>
\[{\mathcal{Y}}_{1}^{*}\]
>
\[\textstyle{J}_{2}^{*}\]
>
\[{\mathcal{Y}}_{3}^{*}\]
>
\[\mathbb{F}\mathbf{\hat{e}}\]
теңсіздіктері саны шектеулі бөлулерден кейін, міндетті түрде алдыңғысы соңғысына қалдықсыз бөлінетін
\[\,T_{n-2}\,,\,P_{n-1}\]
қалдықтары шығатынын көрсетеді:
\[r_{n\cdot2}=r_{n-1}a_{n}\ .\]
Олай болса,
\[\frac{Q}{J}\]
рационал санын көрсететін үздіксіз бөлшек саны шектеулі
\[a_{0},a_{1},a_{2},a_{3},\mathrm{K}\;,a_{n}\]
толымсыз бөлінділерін ғана қамтиды, яғни
\[{\frac{a}{b}}=a_{0}+{\frac{1}{a_{1}+{\frac{1}{a_{2}+{\frac{1}{a_{3}+\mathrm{K}}}{a_{3}+\mathrm{K}+{\frac{1}{a_{n}}}}}}}}\]
Айталық енді,
\[{\mathcal{Q}}\]
- иррационал сан болсын.
\[{\mathcal{Q}}_{0}\]
арқылы
\[{\mathcal{Q}}\]
-дан аспайтын ең үлкен бүтін санды белгілейік, яғни
\[a_{0}=\left[a\right]\]
. Сонда
\[a\;=\;a_{0}+a_{1}\;,\;\;\;0\]
<
\[{\boldsymbol{a}}_{1}\]
<
\[\begin{array}{c}{{\diamondsuit}}\\ {{\langle\S\rangle}}\\ {{\underline{{{\Omega}}}}}\end{array}\]
. (8)
Мұнда
\[{\boldsymbol{a}}_{1}\]
иррационал сан болады, әйтпесе
\[{\mathcal{Q}}\]
рационал сан болған болар еді.
Айталық
\[\frac{1}{\overline{{a_{1}}}}\]
-нің бүтін бөлігі
\[Q_{1}\]
болсын, сонда
\[{\frac{1}{a_{1}}}=\,a+a_{\,2}\,,\]
мұнда
<
\[{\boldsymbol{a}}_{\textbf{2}}\]
<
\[\begin{array}{c}{{\diamondsuit}}\\ {{\langle\S\rangle}}\\ {{\ /\tt\prime}}\end{array}\]
. (9)
Дәл осы сияқты, егерде
\[\frac{1}{a_{_{2}}}\]
-нің бүтін бөлігі
\[{\mathcal{A}}_{2}\]
болса, онда
\[\frac{1}{a_{\:2}}=\;a_{2}+\alpha_{\:3}\;,\]
<
\[{\boldsymbol{a}}_{3}\]
<
\[\begin{array}{c}{{\diamondsuit}}\\ {{\langle\underline{{\bullet}}}}\\ {{\underline{{\cong}}}}\end{array}\]
. (10)
Жоғарыдағыдай, төмендегі теңдіктерді табамыз:
\[\frac{1}{a_{\,3}}=\ a_{\,3}+a_{\,4}\ ,\]
\[\Theta_{}^{}\Theta_{}^{}\]
<
<
\[\begin{array}{c}{{\diamondsuit}}\\ {{\langle\S\rangle}}\\ {{\ /\tt\langle}}\\ {{\langle\Lambda\rangle}}\end{array}\]
,
\[\frac{1}{a_{_4}}=\ a_{4}+\alpha_{5}\ ,\]
<
\[Q_{\varsigma}\]
<
\[\begin{array}{c}{{\diamondsuit}}\\ {{\langle\beta|}}\\ {{\langle\beta|}}\end{array}\]
, (11)
. . .
Мұндағы
\[a_{4}\,,a_{5}\,,\mathrm{K}\]
иррационал сандар
\[a_{3}=\bigl[a_{3}\bigr],\quad a_{4}=\bigl[a_{\ 4}\bigr],\xi\]
\[{\mathcal{Q}}\]
иррационал сан болғандықтан, сандардың бүтін бөлігін табу процесі шектеулі бола алмайды.
(8), (9), (10) және (11) теңдіктерінен біртіндеп,
\[\begin{array}{c}{{a=a_{0}+\displaystyle\cfrac{1}{\left(a_{1}\right)}=a_{0}+\cfrac{1}{a_{1}+\cfrac{1}{\left(a_{2}\right)}}}}\\ {{a_{2}+\cfrac{1}{a_{3}+\cfrac{1}{\left(a_{4}\right)}}}}\end{array}\]
табамыз.
Сөйтіп,
\[{\mathcal{Q}}\]
үшін шектеусіз үздіксіз бөлшек аламыз [8, 272-274б] .
\[{\mathcal{Q}}\]
иррационал санын үздіксіз бөлшекке жіктеуге мысалдар қарастырайық.
Мысал 1.
\[\sqrt{11}\]
-дің жіктелуін табайық.
Шешуі.
\[a={\sqrt{11}}\]
болсын.
\[\sqrt{11}\]
-дің бүтін бөлігін айырып алайық
\[\overline{{\bigcup^{11}}}\underline{{\bigcup_{i=1}}}\]
, ал оның бөлшек бөлігін
\[\frac{1}{a_{_{2}}}\]
түрінде алайық, мұндағы
\[{\sqrt{11}}\ \ -3\]
<
\[\begin{array}{c}{{\diamondsuit}}\\ {{\langle\underline{{{\bullet}}}|}}\end{array}\]
. Сонда
\[\alpha_{\,\,2}=\frac{1}{\sqrt{11-3}}\,\]
>
\[\begin{array}{c}{{\diamondsuit}}\\ {{\langle\phi|}}\\ {{\underline{{{\Omega}}}}}\end{array}\]
. Осы процесті жалғастыра отырып мынаны аламыз.
\[a\,=\!a_{_1}=\sqrt{11}=3+{\frac{1}{a_{_2}}},\quad a_{_2}\]
>
\[\begin{array}{c}{{\diamondsuit}}\\ {{\langle\phi|}}\\ {{\underline{{{\Omega}}}}}\end{array}\]
,
\[a_{2}={\frac{1}{\sqrt{11}-\,3}}={\frac{\sqrt{11}+3}{2}}=3+{\frac{1}{a_{3}}},\quad a_{3}\]
>
\[\begin{array}{c}{{\diamondsuit}}\\ {{\langle\underline{{{\bullet}}}|}}\end{array}\]
,
\[a_{3}=\frac{2}{\sqrt{11}-3}=\frac{2(\sqrt{11}+3)}{2}=6+\frac{1}{a_{4}},\;\;\;a_{4}\]
>
\[\begin{array}{c}{{\diamondsuit}}\\ {{\langle\xi\rangle}}\\ {{\underline{{{\Omega}}}}}\end{array}\]
.
Егер осы қадамда тоқтайтын болсақ,
\[{\mathcal{Q}}\]
санын былай жазуға болады:
\[a\,=3+{\frac{1}{3+{\frac{1}{6+{\frac{1}{a_{4}}}}}}}\]
Екінші жағынан
\[{\boldsymbol{a}}_{3}\]
үшін жазылған формуладан
\[{\sqrt{11}}=3+{\frac{1}{a_{4}}}\]
екенін көруге болады. Сондықтан
\[\sqrt{{\bf\Psi}_{A}}\ \longrightarrow\ \longrightarrow\ U_{a b}\ .\]
болғандықтан, осы кезден бастап толымсыз бөлінділер қайталанып отырады.
Ендеше
\[\sqrt{11}\]
санының үздіксіз бөлшекке жіктелуі
\[\sqrt{1\,1\,}\ =\left[3,\ 3,\ \ 6,\ \ 3,\ \ 6,\ K\right]\]
түрінде болады.
Мысал 2.
\[\frac{24-{\sqrt{15}}}{17}\]
- ті үздіксіз бөлшек түрінде көрсетейік.
Шешуі.
\[\frac{24-{\sqrt{15}}}{17}\]
-тің бүтін бөлігі
\[\begin{array}{c}{{\diamondsuit}}\\ {{\langle\beta|}}\\ {{\langle\beta|}}\end{array}\]
-ге тең, демек
\[{\frac{24-\sqrt{15}}{17}}=1+{\frac{7-\sqrt{15}}{17}}=1+{\frac{1}{7+\sqrt{15}}}=1+{\frac{1}{7+\sqrt{15}}}=1+{\frac{1}{5+\sqrt{15}}}=1+{\frac{1}{5+\frac{\sqrt{15}\cdot3}{2}}}=0{\frac{1}{2}}\]
\[\begin{array}{c}{{\mathrm{}=1+{\cfrac{1}{5+{\cfrac{1}{2-{\cfrac{1}{\sqrt{15+3}}}}}}}}}\\ {{\cfrac{1}{2+{\cfrac{1}{\sqrt{15+3}}}}}}\end{array}\]
Ары қарай үздіксіз бөлшекке жіктеудегі
\[2,\ 3\]
толымсыз бөлінділері шектеусіз қайталанып отырады.
\[\frac{24-{\sqrt{15}}}{17}\]
-тің үздіксіз бөлшекке жіктелуі
\[{\frac{24-\sqrt{15}}{17}}=\left[1;~5,~2,~3,~2,~3,~\mathrm{K}\right]\]
түрінде болады.
Мысал 3.
\[\sqrt{a^{4}+2a}\]
жіктелуін табайық.
Шешуі.
\[\sqrt{a^{4}+2a}=a^{2}+\sqrt{a^{4}+2a}\cdot\ a^{2}=a^{2}+\frac{1}{\sqrt{a^{4}+2a}\cdot a^{2}}=a^{2}+\frac{1}{\sqrt{a^{4}+2a}+a^{2}}=\]
\[\begin{array}{c}{{\displaystyle=a^{2}+\frac{1}{2a^{2}+\sqrt{a^{4}+2a\cdot\;a^{2}}}=a^{2}+\frac{1}{a+\frac{\sqrt{a^{4}+2a}\cdot a^{2}}{2a}}}}\\ {{\displaystyle2a}}\end{array}\]
Көріп отырғанымыздай
\[a,\ \ 2a^{2}\]
толымсыз бөлінділері қайталанып отыр. Бұл теңдіктер ақырында
\[\sqrt{Q^{4}\;+\;2Q}\;=\;\left[\!\!\right]\!\!Q^{2}\;\!\cdot\;\;Q,\;\;\mathcal{D},\;\;\mathcal{D},\;\;\mathcal{D},\;\;\mathcal{D},\;\;\mathcal{D}\mathcal{U}^{2}\,,\left|\!\!\right]\nonumber\]
береді.
\[\frac{\partial^{\mathcal{L}}\mathcal{D}}{\partial r^{\prime}}\]
санының үздіксіз бөлшекке жіктелуін қарастырайық.
Теорема.
\[\frac{e+1}{e-1}=2+\frac{1}{6+\frac{1}{10+K+\frac{1}{4n+2}+K}}\]
Дәлелдеуі.
\[f_{n}(x)\]
-ті
\[(n=0,1,2,\mathrm{K})\]
\[f_{n}(x)={\frac{n!}{(2n)}}+{\frac{(n+1)}{1!(2n+2)}}x^{2}+{\frac{(n+2)}{2!(2n+4)}}x^{4}+\mathrm{K}=\sum_{s=0}^{\infty}{\frac{(n+s)}{s!(2n+2s)}}x^{2s}\]
қатардың қосындысы ретінде анықтайық.
Бұл қатар
\[\textstyle{\mathcal{X}}\]
-тің кез келген мәнінде беттеседі; біз тек
\[\scriptstyle(0,\;1)\]
интервалында жатқан
\[\textstyle{\mathcal{X}}\]
-тің өзін қарастырамыз.
\[f_{n}(x)-\left(4n+2\right)f_{n+1}(x)=4x^{2}f_{n+2}(x)\]
(12)
теңдігінің орындалатынын тексеру оңай.
Шынында да (12) теңдігінің сол жағындағы
\[{\surd\mathcal{N}\rangle}^{\underline{{{2}}}\bar{k}}\]
-ның коэффициенті
тең, ал (12) теңдігінің сол жағындағысы
\[{\frac{4{\big(}n+k+1{\big)}}{(k-1)!(2n+2k+2{\big)}}}={\frac{2(n+k)}{(k-1)(2n+2k+1)}}\]
тең, ендеше (12) дұрыс.
\[\frac{f_{n}\vec{\mathrm{e}}\vec{\mathrm{t}}}{\mathrm{e}}\frac{\vec{\mathrm{o}}}{\mathrm{e}}\]
-ді
\[{\boldsymbol{a}}_{n}\]
арқылы белгілейік. Дербес жағдайда
\[f_{0}(x)=1+{\frac{x^{2}}{2!}}+{\frac{x^{4}}{4!}}+\mathrm{K}={\frac{1}{2}}\Big(e^{x}+e^{-x}\Big)\]
,
\[f_{1}(x)=\frac{1}{2x}\frac{\vartheta}{\bar{\vartheta}}x+\frac{x^{3}}{3!}+\frac{x^{5}}{5!}+\bar{\vartheta}\frac{\bar{\vartheta}}{\stackrel{\circ}{\leq}}=\frac{1}{4x}\Big(e^{x}-e^{-x}\Big)\]
,
болса, онда
\[a_{0}=\frac{f_{0}^{~\dot{\alpha}\dot{1}}\bar{\tilde{\phi}}}{f_{1}^{~\dot{\alpha}}\bar{\tilde{\phi}}}=\frac{e^{\frac{1}{2}}+e^{-\frac{1}{2}}}{1}=\frac{e+1}{e-1}\]
.
\[x={\frac{1}{2}}\]
болғанда (12) теңдігінен
\[a_{n}=(4n+2)+\frac{1}{a_{n+1}}\]
(13)
аламыз.
\[a_{n+1}\]
оң болғандықтан (13) теңдігінен барлық
\[{\cal J}_{\bar{\cal L}}\]
үшін
\[{\boldsymbol{a}}_{n}\]
>
\[4n+2\]
>
\[1,{\frac{1}{a_{n+1}}}\]
<
\[\left|\mathbf{\varepsilon}\right|_{\Sigma}\]
яғни
көрсетеді және
\[n=0,1,2,K\]
болғанда (13) қатынасының тізбегі
\[a_{0}=2+{\frac{1}{a_{1}}}\]
\[a_{1}=6+{\frac{1}{a_{2}}}\]
\[a_{2}=10+{\frac{1}{a_{3}}}\]
. . .
\[{\boldsymbol{a}}_{0}\]
-дің үздіксіз бөлшекке жіктелуін береді:
\[\frac{e+1}{e-1}=a_{0}=2+\frac{1}{6+\frac{1}{10+\mathrm{K}+\frac{1}{4n+2}+\mathrm{K}}}\]
(14)
Теорема.
\[e=2+{\cfrac{1}{1+{\cfrac{1}{1+{\cfrac{1}{1+{\cfrac{1}{4+{\cfrac{1}{1+{\cfrac{1}{6+\mathrm{C}}}}}}}}}}}}}\]
(15)
яғни
\[\frac{\partial^{\mathcal{L}}\partial}{\partial r^{\prime}}\]
санының үздіксіз бөлшекке жіктелуіндегі
\[Q_{n}\]
элементтері
\[a_{0}=2,\ \ a_{3n}=a_{3n+1}=1\]
және
түрінде жазылады.
Дәлелдеуі. (15) жіктелуінің оң жағының лайықты бөлшектерін
\[{\frac{P_{n}}{Q_{n}}}\]
арқылы, ал (14) жіктелуінің лайықты бөлшектерін
\[\frac{R_{n}}{S_{n}}\;\left(n=0,1,2,\mathrm{K}\right)\]
арқылы белгілейік.
\[\frac{R_{n}}{S_{n}}=\frac{P_{3n+1}+Q_{3n+1}}{P_{3n+1}-Q_{3n+1}}\]
орындалатынын дәлелдейік.
(15) үздіксіз бөлшегінің элементтерінің мәніне көңіл аудара отырып
\[\begin{array}{l}{{P_{3n+1}=P_{3n}+P_{3n-1},\ P_{3n}=P_{3n-2},}}\\ {{P_{3n-1}=2n P_{3n-2}+P_{3n-3},}}\\ {{P_{3n-2}=P_{3n-3}+P_{3n-4},\ P_{3n-3}=P_{3n-4}+P_{3n-5},}}\end{array}\]
жаза аламыз, одан
\[\begin{array}{l c r}{{P_{3n+1}=2P_{3n-1}+P_{3n-2}=\left(4n+1\right)P_{3n-2}+2P_{3n-3}=}}\\ {{=(4n+2)P_{3n-2}+P_{3n-4}=(4n+2)P_{3n-2}+P_{3n-5}}}\end{array}\]
табамыз.
Осыған ұқсас қатынасты
\[\textstyle\mathbb{Q}_{3n+1}\]
үшін де аламыз, сондықтан
\[\begin{array}{l}{{P_{3n+1}=(4n+2)P_{3n-2}+P_{3n.5},\quad\ddot{\mathrm{u}}}}\\ {{O_{3n+1}=(4n+2)O_{3n.2}+Q_{3n-5}.\quad\nonumber}}\end{array}\]
(16)
\[R_{n}=\frac{1}{2}\left(P_{3n+1}+Q_{3n+1}\right)\]
(17)
\[{\cal J}_{\bar{\cal L}}\]
бойынша индукциямен дәлелдейік.
(14) және (15) -ден
\[R_{0}=2,\ R_{1}=13,\ P_{1}=3,\ P_{4}=19,\ Q_{1}=1,\ Q_{4}=7\]
есептейміз, ендеше (17) қатынасы
\[n=0\]
және
\[\textstyle n=1\]
үшін дұрыс.
(17) қатынасы
\[{\cal J}_{\bar{\cal L}}\]
-нен кіші болатын барлық
\[\textstyle{\mathcal{D}}\]
номерлері үшін дұрыс деп ұйғарайық, мұндағы
\[n\geq2\]
, яғни көбінесе
\[R_{n-1}={\frac{1}{2}}\left(P_{3n-2}+Q_{3n-2}\right),\]
\[R_{n-2}={\frac{1}{2}}\left(P_{3n-5}+Q_{3n-5}\right);\]
онда (16) теңдігін қолдана отырып
\[R_{n}=(4n+2)R_{n-1}+R_{n-2}={\frac{1}{2}}\left\{(4n+2)(P_{3n-2}+Q_{3n-2})+P_{3n-5}+Q_{3n-5}\right\}={\frac{1}{2}}\left(P_{3n+1}+Q_{3n+1}\right\}\]
аламыз.
Толық математикалық индукция принципіне байланысты (17) теңдігі барлық
\[{\mathcal{N}}\]
үшін дұрыс.
\[S_{n}=\frac{1}{2}\left(P_{3n+1}-Q_{3n+1}\right)\]
теңдігі де дәл солай дәлелденеді.
\[\textstyle R_{n}\]
және
\[\textstyle S_{n}\]
шамаларының қатынасының шегін қарастыра отырып мынаны табамыз:
яғни
\[\operatorname*{lim}_{n\to\infty}{\frac{P_{3n+1}}{Q_{3n+1}}}=e\]
.
(15) үздіксіз бөлшегінің оң бөлігі беттесетіндіктен, және біз
\[\operatorname*{lim}_{n\to0}{\frac{P_{n}}{Q_{n}}}=e\]
аламыз, осының бәрі теореманың дәлелдері бола алады [1, 221-223б] .
1. 2 Шектеусіз үздіксіз бөлшектердің лайықты бөлшектері
Шектеулі немесе шектеусіз үздіксіз бөлшек берілсін:
\[a\,=a_{0}+{\frac{1}{\,a_{1}+{\frac{1}{\,a_{2}+\mathrm{{K}}}}}}=\left[a_{0};{a_{1}},{a_{2}},\mathrm{K}\right]\]
. (1)
Бұл үздіксіз бөлшектің алғашқы
\[k+1\]
толымсыз бөліндісінен құралған шектеулі үздіксіз
\[\left[a_{0};\,a_{1},\,a_{2},\mathrm{K}\,,a_{k}\right]\]
бөлшегін
\[{\mathcal{N}}\]
нөмірлі лайықты бөлшек деп атап,
\[{\frac{P_{k}}{Q_{k}}}\]
деп белгілейді:
Дербес жағдайда,
Шектеулі үздіксіз бөлшектің саны шектеулі лайықты бөлшегі, ал шектеусіз
үздіксіз бөлшектің саны шектеусіз лайықты бөлшегі болатыны түсінікті. (1) үздіксіз бөлшек шектеусіз үздіксіз бөлшек болса, оның мәнін төмендегі лайықты бөлшектер шегі ретінде қарастыруға болады:
\[{\frac{P_{0}}{Q_{0}}},\;{\frac{P_{1}}{Q_{1}}},\;{\frac{P_{2}}{Q_{2}}},\;{\frac{P_{3}}{Q_{3}}},\;\mathrm{K}\;,{\frac{P_{k}}{Q_{k}}},\mathrm{K}\]
\[a=\operatorname*{lim}_{k\oplus\lnot}{\frac{P_{k}}{Q_{k}}}.\]
(1) үздіксіз бөлшектің
\[k+1\]
-ден бастап барлық келесі толымсыз бөлінділерінен құралған
\[a_{{\mathit{k+1}}}=\left[a_{{\mathit{k+1}}};\,a_{{\mathit{k+2}}},\,a_{{\mathit{k+3}}},\mathbf{K}\right]\]
үздіксіз бөлшегін толық бөлінді деп атайды.
(1) үздіксіз бөлшекті
\[a_{\ k+1}\]
толық бөлінді арқылы шектеулі үздіксіз бөлшек түрінде көрсетуге болады:
\[a=\left[a_{0};a_{1},a_{2},{\bf X}\;a_{k},a_{k+1}\right]=a_{0}+\frac{1}{a_{1}+\frac{}{}a_{2}+{\bf X}+\frac{1}{a_{k}+\frac{1}{}a_{k+1}}}{a_{k+1}}\]
мұндағы
\[{a_{\ k+1}}=\left[a_{k+1};\,a_{k+2},\,a_{k+3},\kappa\right]\]
.
Егерде
\[{\mathcal{Q}}\]
шектеулі үздіксіз бөлшек болса, онда оның барлық толық бөлінділері де шектеулі үздіксіз бөлшектер болады, ал
\[{\mathcal{Q}}\]
шектеусіз үздіксіз бөлшек болса, онда толық бөлінділері шектеусіз үздіксіз бөлшектер болады.
\[\textstyle{\mathcal{D}}_{k}\]
мен
\[{\mathcal{Q}}_{k}\]
-ның мәндерін кесте бойынша да есептеуге болады.
Кесте 1. 1 Лайықты бөлшектерді есептеу
\[\mathbb{F}\mathbf{\hat{e}}\]
:
\[\textstyle{\mathcal{D}}_{k}\]
:
\[Q_{2}{\cal P}_{1}\,+\,{\cal P}_{0}\]
:
\[\mathbb{I}\mathbf{\hat{X}}\]
:
\[\begin{array}{c}{{\diamondsuit}}\\ {{\langle\beta|}}\\ {{\langle\beta|}}\end{array}\]
:
\[A_{3}{\underline{{\phi}}}_{2}+\underline{{\theta}}_{0}\]
:
\[\mathbb{I}\mathbf{\hat{X}}\]
1. 3 Лайықты бөлшектердің қасиеттері
Лайықты бөлшектердің қасиеттеріне тоқталайық.
\[{\mathfrak{I}}^{0}.\]
Тетелес
\[{\frac{P_{k-2}}{Q_{k-2}}}{\frac{P_{k-1}}{Q_{k-1}}},{\frac{P_{k}}{Q_{k}}}\]
үш лайықты бөлшектің алымдары
мен бөлімдері
\[Q_{k-2},Q_{k-1},Q_{k}\]
өзара
\[\begin{array}{c}{{\mathrm{i}\,P_{k}=P_{k-1}a_{k}+P_{k-2}}}\\ {{\mathrm{i}\,(Q_{k}=Q_{k-1}a_{k}+Q_{k-2}}}\end{array}\]
(1)
... жалғасы
Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.
Ұқсас жұмыстар
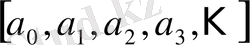деп те белгілейді. Олай болса,
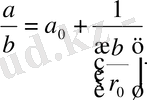(3)
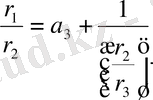-нің мәнін (6) -ға қойып,
(7)
<
<
<
<
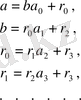
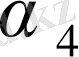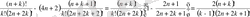
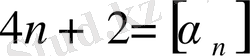көрсетеді және
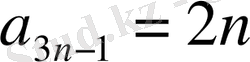түрінде жазылады.
,
.
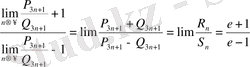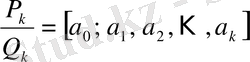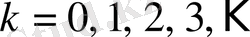болса,
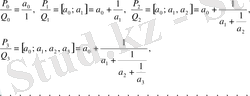
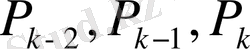мен бөлімдері
