Логарифмдік және көрсеткіштік теңдеулер мен теңсіздіктерді шешу әдістері


Қазақстан Республикасы білім және ғылым министрлігі
М. Өтемісов атындағы Батыс Қазақстан мемлекеттік университеті
Курстық жұмыс
Тақырыбы: Логарифмдік және көрсеткіштік теңдеулер мен теңсіздіктерді шешу әдістері
Орындаған:
Жетекшісі:
Орал - 2016
Мазмұны
Кіріспе . . . 3
1 Логарифдік және көрсеткіштік функцияның қалыптасуы
1. 1Логарифмдік функция және олардың қасиеттері . . . 5
1. 2 Натурал және ондық логарифмдер . . . 12
1. 3 Көрсеткіштік функция және көрсеткіштік функцияның графигі . . . 15
2 Логарифмдік және көрсеткіштік теңдеулер мен теңсіздіктерді шешу әдістері
2. 1 Логарифмдік және көрсеткіштік теңдеулер мен теңсіздіктерді шешу . . 24
2. 2 Көрсеткіштік теңсіздіктер . . . 26
2. 3 Логарифмдік теңдеулерді шешу және құрастыру . . . 29
Қорытынды . . . 32
Пайдаланылған әдебиеттер тізімі . . . 33
Кіріспе.
Еліміздің егемендікке ие болып, Қазақстан өз алдына мемлекет мәртебесіне жетіп бүкіл әлемге, жер жүзіне өзінің елдігін, саясатын танытатын шаққа жетіп отыр. Еліміздің елдігін танытып, оны жетілдіріп, дамытатын жас ұрпақ сондықтан да еліміздің болашағы жас жеткіншектің білім дәрежесінің тереңдігімен өлшенеді. Ал осы балғын жеткіншектерге жол көрсетуші, бағыт беруші мектеп мұғалімдері.
Сондықтан адал ниет жас жеткіншектерге білім мен тәрбие есігін ашу мектеп мұғалімдеріне абыройлы да жауапты жұмыс жүктейді. Өйткені білім тәрбиенің негізі, демек баланың жеке басының қалыптасу кезеңі мектеп қабырғасында қаланады.
Біз біліктілікті қалыптастыратын бірғана математика саласын қарастырып отырмыз. Оның білімділікке қосатын үлесі қандай деген сауал тілімізге оралады. Бағдарлама бүреудің ойпікірі. Оның материалын жүйелеп бергенде болған. Мұндай жағдайда оқырманның өзіне тән обьективтік пікір қалыптаспайды. Адам есепті өзі құрастырса, онда ол есеп құрамындағы өрнектерді өзінің бұрын оқыған математикалық сөйлемдеріндегі, формулалардың, теоремалардың құрамындағы өрнектермен салыстырып олардың теңдеулер құрамына қосатын үлесін анықтап біреудің айтуы бойынша емес өз басымен ойлап тапқан шешімді шешім қабылдайды.
Тақырыптың өзектілігі: логирифм және көрсеткіш ұғымы мектеп курсында 10 - 11-шы сыныптарда оқытылады, логарифмның және көрсеткіштіктің өзектілігі күрделі алгебралық теңдеулер мен теңсіздіктерді шешкенде маңызды рөл атқарады. Теңдеулерді шешуде негізінен екі түрлі тәсіл жиі қолданылады. Бұл екі тәсілде де берілген күрделі теңдеулерді қарапайымдау бірнеше теңдеулер жиынтығына келтіріп шешеді. Сондықтан логарифмдік және көрсеткіштік теңдеулерді түрлендіру барысында олардың тең шамалылығын қадағалай отырып, функцияларға тән қасиеттерді де қолдану керек. Әрине, білімімізді кеңейту арқылы ойлау заңдылығының өрбуінің және оның дамуын үйренеміз. Зерттеу нәтижесінде логарифмдік және көрсеткіштік теңдеулерді әртүрлі жолдарымен алынған тәсілінің мәнін ашпақты.
Курстық жұмыстың мақсаты: мектеп курсындағы логарифмдік және көрсеткіштік теңдеулер мен теңсіздіктерді әдіс-тәсілдерін үйрету. Оқушылардың теорияда алған білімдерін, дағдыларын қалыптастыру және ойлау қабілеттерін дамыту.
Курстық жұмыстың маңыздылығы: оқушыларды математика пәні бойынша алған теориялық білімін, дағдыларын қалыптастыру және өз бетімен алған білімін практикада тиімді пайдалану.
Зерттелу деңгейі: Логарифмдік және көрсеткіштік теңдеулер мен теңсіздіктерді шешудің әдіс-тәсілдерін көрсету. Мектепте оқушылардың логикалық ойлау қабілетін дамытатындай логарифмдік және көрсеткіштік теңдеулер мен теңсіздіктерді құру. Математика ғылымының белгілі бір даму дәрежесіне лайық қоғамның алға қойған мақсаттарына сай математиканы оқытудың заңдылықтарын зерттеу.
Курстық жұмыстың құрылымы: кіріспеден, 2 тараудан және қорытындыдан, пайдаланылған әдебиеттер тізімінен тұрады.
Күтілетін нәтиже: оқушылардың білімін обьективті түрде айқындау, бағалау және логаримдік және көрсеткіштік теңдеулер мен теңсіздіктерді түрлі әдіс тәсілдермен шығара білу.
1. Логарифдік және көрсеткіштік функцияның қалыптасуы
1. 1 Логарифмдік функция және олардың қасиеттері
Логарифм (logos -
қатынас
және arіthmos -
сан
), N санының
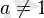 негізі бойынша логарифмі - N санын алу үшін а саны m дәреже (Логарифм негізі), бұл log
a
N түрінде белгіленеді. Сонымен, егер a
m
=N болса, m=log
a
N. а<0 болғанда шексіз көп оң сандардың нақты логарифмі болмас еді, сондықтан да a>0 деп алынады. Логарифмдік функциялардың қасиеті бойынша, кез келген оң санның берілген негізі бойынша бір ғана нақты Логарифмі болады (теріс санның Логарифмі Логарифмді ойлап тапқан және логарифмдік кесте құрастырған ғалым туралы қысқаша айта кетейік. Джон Непер - шотландияда туған. 16 жасында континентке кетіп, 5 жыл Европаның әртүрлі университеттерінде оқып, математиканы игерген. Кейін астрономия және математикамен терең айналысқан. Логарифмдік есептеулер идеясына Непер 16-ғасырдың 80-жылдарында келген, дегенмен өзінің кестесін 25 жыл есептеулерден кейін 1614 жылы ғана жариялаған. Ол «Логарифмдік керемет кестелер сипаты» деген атпен шыққан. «Логарифм» деген терминнің өзін де Непер ұсынған, ол оны «қолдан жасалған сан» деп аударған. Непердің кестелері мен идеялары тез таралып, қолданықа түскен. «Непер ережесін» және «Непер аналогияларын» сфералық тригонометрияда кездестіруге болады. логарифмдік терминнің («сандардың қатынасы»деген мағынаны білдіреді) тұңғыш ұсынған ғалым. Гректің екі сөзінің бірігуінен құралған: -сан және - қатынас. Бюрги және Непер еңбектері есептеу жұмыстары анағұрлым жеңілденді. Уақыт өте келе, ол кең етек жая бастады. Логарифм көбінесе физикалық есептерді шығарғанда және химиялық, биологиялық басқа да процестерге математикалық сипаттама берген кезде қолданылады. Логарифмдік функциялардың қасиеттеріне түрлендірулер жүргізген кезде, сондай-ақ теңдеулер, теңсіздіктер және олардың жүйелерін шешуде қолданылуда.
негізі бойынша логарифмі - N санын алу үшін а саны m дәреже (Логарифм негізі), бұл log
a
N түрінде белгіленеді. Сонымен, егер a
m
=N болса, m=log
a
N. а<0 болғанда шексіз көп оң сандардың нақты логарифмі болмас еді, сондықтан да a>0 деп алынады. Логарифмдік функциялардың қасиеті бойынша, кез келген оң санның берілген негізі бойынша бір ғана нақты Логарифмі болады (теріс санның Логарифмі Логарифмді ойлап тапқан және логарифмдік кесте құрастырған ғалым туралы қысқаша айта кетейік. Джон Непер - шотландияда туған. 16 жасында континентке кетіп, 5 жыл Европаның әртүрлі университеттерінде оқып, математиканы игерген. Кейін астрономия және математикамен терең айналысқан. Логарифмдік есептеулер идеясына Непер 16-ғасырдың 80-жылдарында келген, дегенмен өзінің кестесін 25 жыл есептеулерден кейін 1614 жылы ғана жариялаған. Ол «Логарифмдік керемет кестелер сипаты» деген атпен шыққан. «Логарифм» деген терминнің өзін де Непер ұсынған, ол оны «қолдан жасалған сан» деп аударған. Непердің кестелері мен идеялары тез таралып, қолданықа түскен. «Непер ережесін» және «Непер аналогияларын» сфералық тригонометрияда кездестіруге болады. логарифмдік терминнің («сандардың қатынасы»деген мағынаны білдіреді) тұңғыш ұсынған ғалым. Гректің екі сөзінің бірігуінен құралған: -сан және - қатынас. Бюрги және Непер еңбектері есептеу жұмыстары анағұрлым жеңілденді. Уақыт өте келе, ол кең етек жая бастады. Логарифм көбінесе физикалық есептерді шығарғанда және химиялық, биологиялық басқа да процестерге математикалық сипаттама берген кезде қолданылады. Логарифмдік функциялардың қасиеттеріне түрлендірулер жүргізген кезде, сондай-ақ теңдеулер, теңсіздіктер және олардың жүйелерін шешуде қолданылуда.
1. b санының негізі а болғандағы логарифмі дегеніміз - b саны шығу үшін негіз шығарылатын дәреже көрсеткіш. a негіздегі b санының логарифмі log a b деп белгіленеді.
2. Егер a > 0, a ≠ 1, b > 0, онда
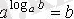 теңдігі логарифмнің негізгі теңбе-теңдігі деп атайды.
теңдігі логарифмнің негізгі теңбе-теңдігі деп атайды.
Мысалы,
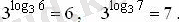
3. Ондық логарифмді log 10 b, мұндағы b - кез-келген оң сан, lg b деп жазады.
Логарифмдік функция, қасиеттері
1. log a N - негізі a > 1 әрі N > 1 болса, онда логарифмнен оң сандар, ал 0<N < 1 болса, онда теріс сандар шығады. Мысалы, . 2. log a N - негізі 0 < a < 1 әрі N > 1 болса, онда логарифмнен теріс сандар, ал a < N < 1 болса, онда оң сандар шығады.
Мысалы,
3. Егер a > 1, онда log a N 1 < log a N 2 теңсіздігінен N 1 > N 2 екені шығады.
Мысалы: log 3 7 > log 3 5 осыдан 7>5.
4. Егер 0 < a < 1, онда log a N 1 < log a N 2 теңсіздігінен екені шығады.
Мысалы: осыдан 9>7.
5. log a 1 = 0 (a>0, a ≠ 1) .
6. log a a = 1 (a>0, a ≠ 1) .
y = log a x функциясының қасиеттері, егер a>1:
А) D(f) = R + ;
Б) E(f) = R;
В) функция өспелі;
Г) егер x = 1болса, онда log a x = 0;
Д) егер 0 < x < 1 болса, онда log a x < 0;
Е) егер x > 1 болса, онда log a x > 0.
y = log a x функциясының қасиеттері, егер 0 < a < 1:
А) D(f) = R + ;
Б) E(f) = R;
В) функция кемімелі;
Г) егер x = 1 болса, онда log a x = 0;
Д) егер 0 < x < 1 болса, онда log a x > 0;
Е) егер x > 1 болса, онда log a x < 0.
Логарифм формулалары:
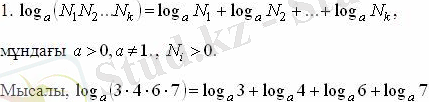


Логарифмнің негізгі қасиеттері:
(яғни сандарды көбейту және бөлу Л-ін олардың Л-дерін қосу мен алуға, ал дәрежеге шығару мен түбір табу Логарифмін сол дәреже немесе түбір көрсеткішіне көбейту мен бөлуге, яғни барынша қарапайым амалдарға келтіруге мүмкіндік береді) . Егер a негізі белгілі болса, анықталған Логарифм жүйесі туралы айтуға болады. Әдетте lgN түрінде белгіленетін ондық Логарифм (a=10) көбірек қолданылады. (k - бүтін сан) санынан басқа рационал санның ондық Логарифмі ондық бөлшек түрінде жуықтап өрнектелетін трансцендент сан. Ондық Логарифмнің бүтін бөлігін сипаттамасы, ал бөлшек бөлігін мантиссасы деп атайды.
lg( N) =k+lgN
болғандықтан, көбейткішімен ерекшеленетін сандардың ондық логарифмінің мантиссасы бірдей, тек сипаттамалары әр түрлі болады. Логарифм кестелері осы қасиетке негізделіп жасалған, онда бүтін сандардың тек мантиссалары ғана берілген.
Негізі e=2, 71828 . . . трансцендент сан болатын натурал логарифмнің де маңызы зор; ол lnN түрінде белгіленеді. Логарифмнің бір негізінен екінші негізіне ауысу үшін
формуласы қолданылады. көбейткіші a негізден b негізге ауысу (өту) модулі деп аталады. Натурал логарифмнен ондық логарифмге немесе керісінше өту , lgN= ; =2, 30258; =0, 43429 . . . формулалары арқылы жүзеге асырылады.
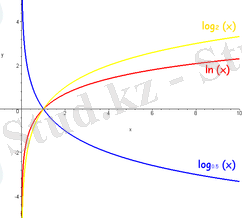
Логарифм атауын Дж. Непер ұсынған. Логарифм ең алдымен 16 ғасырда астрономияның тез дамуымен, астрономия бақылауларды анықтай түсуге және астрономия есептеулердің күрделілене түсуіне байланысты ашылды. Алғашқы Логарифм кестелерінің авторлары геометриялық прогрессия қасиеттері мен оның мүшелерінің дәреже көрсеткіштерінен құрастырылған арифметикалық прогрессия қасиеттерінің арасындағы тәуелділікті пайдаланған. Бұл тәуелділіктерді б. з. б. 3 ғасырда Архимед ішінара байқаған болатын, 1484 ж. Н. Шюке, 1544 ж. М. Штифель оларды жақсы білген. Алғашқы Логарифм кестелерін 1614 - 1619 ж. Дж. Непер мен 1620 ж. Й. Бюрги бір-біріне тәуелсіз және бір мезгілде құрастырған. Логарифмді теория тұрғыдан зерттеуде Бельгия математигі Григорий мен Л. Эйлер (1707 -1783) еңбектерінің маңызы зор.
Логарифмдік функция - x = көрсеткіштік функциясына кері y=lnx функциясы. х аргументінің белгілі бір мәніне сәйкес келетін у логарифмдік функцияның мәні х санының натурал логарифмі деп аталады. Логарифмдік функцияның негізгі қасиеттері көрсеткіштік функция мен логарифмдердің қасиеттерінен шығады. Математика анализ курсында
(мұндағы x>0, а>0) Логарифмдік функциясы қарастырылады. Бұл функция y=lnx Логарифмдік функциямен қатынасы арқылы байланысады. Логарифмдік функциясы x>0 болғанда анықталған, бірсарынды (монотонды) (а>1 болғанда өседі, 0<а<1 болғанда кемиді), үзіліссіз және шексіз дифференциалданады. Логарифмдік функция өзінің анықталу облысындағы әрбір нүктенің маңайында дәрежелік қатарға жіктелуі мүмкін.
Қарапайым логарифмдік теңдеу және теңсіздіктің мәндес өзгерісінің орындалу схемасы
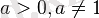
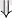
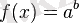
(
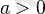 болғандықтан, онда
болғандықтан, онда
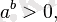 және сондықтан ақырғы теңдеудің (ММЖ) (ОДЗ) автоматты түрде ескеріледі. )
және сондықтан ақырғы теңдеудің (ММЖ) (ОДЗ) автоматты түрде ескеріледі. )
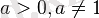
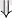
 немесе
немесе
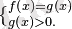
- , мұнда
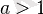 онда
онда
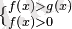 Теңсіздің таңбасы өзгермейді және (ММЖ) (ОДЗ) есептеледі
Теңсіздің таңбасы өзгермейді және (ММЖ) (ОДЗ) есептеледі
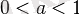 онда
онда
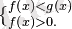 Теңсіздің таңбасы өзгереді және (ММЖ) (ОДЗ) есептеледі
Теңсіздің таңбасы өзгереді және (ММЖ) (ОДЗ) есептеледі
Осы бөлімде оң санның логарифмінің анықтамасы мен логарифмнің қасиеттерін қарастырамыз. Аталған анықтама мен қасиеттерді білу логарифмдік өрнектерді түрлендірулерге, логарифдік функцияларды зерттеуге, логарифмдік теңдеулер мен теңсіздіктерді және олардың жүйелерін шешуге қатысты есептерді қарастырғанда қажет болады. «Логарифм» тақырыбы 11-сыныптың материалы екендігін білеміз және бұл тақырыпты түсіну үшін 7-сыныпта өткен дәреже мен оның қасиеттерін жақсы білудің маңызды екендігін атап кетеміз.
Анықтама. Оң санының негізі бойынша логарифмі деп санын алу үшін а санын дәрежелеу керек болатын с дәреже көрсеткіші аталады:

а - логарифм негізі, логарифмденетін сан.
Мұндағы а санының оң болу себебі: егер а теріс болса, онда, мысалы, а 1/2 өрнегінің мағынасы жоқ, себебі теріс санның квадраттық түбірі анықталмаған; ал егер а =0 болса, онда, мысалы а -1 өрнегінің мағынасы жоқ, себебі нөлге бөлуге болмайды ғой! саны да оң сан болады, себебі ол оң а санының дәрежесі, ал оң санның кез келген дәрежесі оң сан болатындығын біз білеміз.
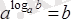 -
негізгі логарифмдік теңбе-теңдік
.
-
негізгі логарифмдік теңбе-теңдік
.
10 негізі бойынша алынған логарифм ондық логарифм деп аталып, былай белгіленеді:
е негізі бойынша алынған логарифм натурал логарифм деп аталып, былай белгіленеді:
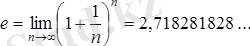
е санының рөлі (яғни ғылым мен техникада алатын орны) π санының рөлінен артық болмаса, кем емес екендігін атап кетеміз.
Жаңа негізге көшу формуласы:
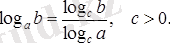
Жаңа негізге көшу формуласының дербес жағдайы: Егер b=c болса, онда
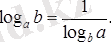
Соңғы теңдіктен log a b ∙log b a =1 теңдігін аламыз, бұл log a b және log b a сандары өзара кері сандар дегенді білдіреді (екі санның көбейтіндісі 1-ге тең болса, олар өзара кері сандар деп аталатындығын еске сала кетеміз), бұдан өз кезегінде log a b және 1/log b a сандары өзара кері сандар екендігі шығады.
1. 2 Натурал және ондық логарифмдер
Натурал логарифм - негізі e=2, 71826… саны болатын логарифм. N санының Натурал логарифмі lnN деп белгіленеді. 1-ден 1000-ға дейінгі сандардың Натурал логарифмінің алғашқы таблицасын Дж. Спейдель жасаған (1619) . Натурал логарифм атауын 1659 жылы П. Менголи (1625 - 1686) және 1668 жылы Н. Меркатор (1620 - 1687), ал ln белгіленуін 1893 ж. А. Прингсхейм (1850 - 1941) енгізген.
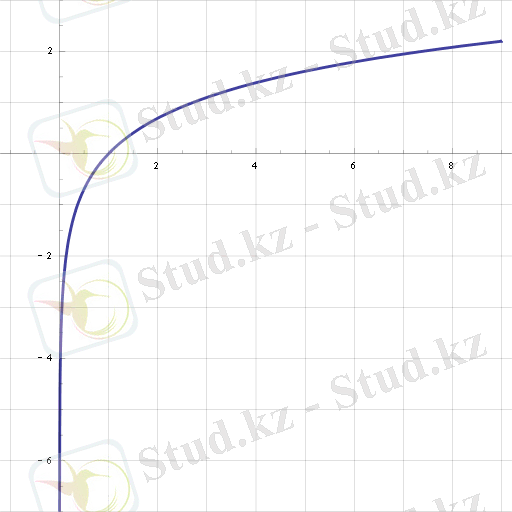
Натурал логарифм функциясының графигі
Ондық логарифм - негізі онға тең логарифм, яғни берілген сан шығуы үшін онның дәрежеленетін дәреже көрсеткіші. Мысалы, lg100=2. N санының Ондық логарифмі lgN таңбасы арқылы жазылады. Басқаша айтқанда b санының ондық логарифмы деп ~ =b теңдеуі шешімін айтады.
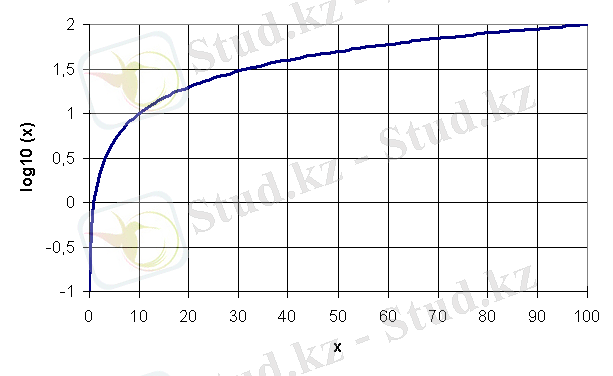
lg e = 0. 4343… саны ондық логарифмдердің модулі деп аталып, М әрпімен белгіленеді:
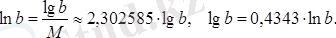
Логарифмдердің қасиеттері :
Бұл қасиеттердің дәлелдеулерін келтірмейміз. Бірақ осы қасиеттердің дәлелдеулерін білудің осы тақырыпқа, яғни логарифмге қатысты есептерді шешу барысында көп көмегі тиетіндігін айта кетеміз.
Логарифмдік функцияның туындысы. Логарифмдерді кейбір тамаша шекте қолдану
Көрсеткіштік функция туындысы:
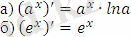
Логарифмдік фукнция туындысы:
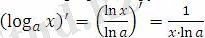
мұндағы, бөліміндегі lna - сан болғандықтан,
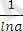 коэффициент ретінде алуға болады да, тек қана алымы lnx- тен ғана туынды алуға болады.
коэффициент ретінде алуға болады да, тек қана алымы lnx- тен ғана туынды алуға болады.
1. 3 Көрсеткіштік функция және көрсеткіштік функцияның графигі.
Ғылым мен техниканың көптеген салдарынан әртүрлі құбылыстар мен процестреді қарастырғанда, процестерді сипаттайтын екі айнымалы шаманың арасындағы функционалдық тәуелділік байқалады. Осыған байланысты мысалдар келтірейік:
- теңіз деңгейімен артуына қарай p атмосфералық қысымp=p0ahp_{0}a^{h}заңы бойынша өзгереді, мұндағыp0p_{0\ }- теңіз деңгейіндегі қысым, a- тұрақты шама;
- ағашты өнеркәсіпте қолдану шамасы A =A0aktA_{0}a^{kt}заңдылығына сәйкес өседі, мұндағыt- уақыт, A0A_{0}- ағаштың бастапқы саны, А -уақыт өтуіне қарайм3м^{3}-пен өзнектелетін ағаш санының өзгерісі;
- радийдың ыдырауыx =x0aktx_{0}a^{kt}заңдылығына сәйкес өтеді, мұндағыx0x_{0}саныt =0 болғандағы радий атомдарының бастапқы саны, aжәнеk- тұрақты сандар.
Келтірілген мысалдардағы процестер органикалық өсу прщцесіне жатады. Органикалық өсу процесін сипаттайтын айнымалылардың физикалық мағынасынан ауытқып, оларды x және y әріптерімен белгілесек, онда кез келген органикалық өсу мына функцияны береді:
y = C
Осындай функцияның C =k = 1болғандағы қарапайым түрін, яғни y = функциясын қарастырайық
Анықтама. y = ( a ) түрінде берілген функцияны көрсет-кіштік функция деп аталады.
Көрсеткіштік функция, экспоненциялық функция, экспонента - y = функциясы [мұндағы е (натурал логарифмдердің негізі) - Непер саны] . z-тің кез келген (нақты немесе комплекс) мәні үшін ол y = формуласы бойынша анықталады. z=1 болса, көрсеткіштік функцияның мәні e=2, 7182 . . . болады. . Көрсеткіштік функцияға кері функция логарифмдік функция деп аталады.
y ═ log a x логарифмдік функция y ═ log 2 x
y
2 x y
1 0
1 y ═ log 2 x , a ˃1 2 1
x 4 2
-2 -1 О 1 2 1
-1 2 -1
1
-2 4 -2
y ═ a x көрсеткіштік функция y ═ 2 x
y
2
1
О x
-2 -1 1 2
-1
-2
Енді екі функцияның графигін координаталық жазықтыққа салсақ, y═x түзуіне қарағанда симметриялы графиктер шығады.
y
y═
2 y ═x
y═log 2 x
1
O x
-2 -1 1 2
-1
-2
0 ˂ a ˂1
y = + y
2
y ═ x
1
O
x
-2 -1 1 2
-1 y═log 1 x
2
-2
Логарифмдік функцияның қасиеттері :
1) Д ( log a x ) - барлық оң сандар жиынтығы R + 0; + ∞
2) Е ( log a x ) - барлық нақты сандар жиынтығы R -∞; + ∞
3) а ˃1 болса, функция өспелі болады, 0 ˂ а ˂ 1 функция кемиді.
4) Функция өзінің анықталу облысында үзіліссіз
y y ═ x 0, 5
1
O x
-1 1
-1
y ═ 2 x
y
y═2 x
1
x
-1 O 1
-1
y
y ═ log 2 x
1
O
-1 1 x
-1
y
1
-1 O 1 x
-1
y
y ═ log 2 x 0 ˂ a ˂ 1
1
x
-1 O 1
-1
y
y ═ x
1
-1 O 1 x
-1
y
y ═ log 2 x
1
O x
-1 1
-1
y
y═x 3
1
O x
-1 1
-1
y
1 y ═ x 2
O x
-1 1
-1
Мысалдар:* y ═ f(x) функциясының анықталу облысын табыңдар
1) f(x) ═log 2 (x+1)
D(f) ═?
Шешуі: х + 1˃0
х˃-1
жауабы: (-1; + ∞)
2) f(x) ═log 0, 7 (x-8)
D(f) ═?
Шешуі: х -8 ˃0
х˃8
жауабы: (8; + ∞)
3) f(x) ═
D(f) ═?
Шешуі: 3х + 4˃0
3х˃-4
x> -
жауабы: (- ; + ∞)
4) f(x) ═log 5 (2x-1)
D(f) ═?
Шешуі: 2х -1 ˃0
2х˃1
х˃0, 5
жауабы: (0, 5; + ∞)
Есеп
1) f(x) ═
D(f) ═?
Шешуі: 2 - х ˃0
-х˃-2
х ˂2
жауабы: (- ∞; 2)
2 ) f (x) ═log 2, 5 (5 - 2x)
D(f) ═?
Шешуі: 5 - 2х ˃0
-2х˃-5
х ˂2, 5
жауабы: (- ∞; 2, 5)
Есеп
1) f(x) ═lg (3x - 1) + lg (x 2 + x + 1)
D(f) ═?
Шешуі: D(f) ═ 3x - 1˃0 => 3x > 1 =˃ x ˃ 1
x 2 + x +1˃0 x > 0 3
x > 0
жауабы: 1 + ∞
3;
2 Логарифмдік және көрсеткіштік теңдеулер мен теңсіздіктерді шешу әдістері
2. 1 Логарифмдік және көрсеткіштік теңдеулер мен теңсіздіктерді шешу
Ең қарапайым логарифмдік теңдеуді қарастырайық. Логарифмдік функция (0; ∞) аралығында өседі (не кемиді) және осы аралықта барлық нақты сандарды қабылдайды. Түбір туралы теорема бойынша, бұдан кез келген b үшін берілген теңдеудің түбірі бар және ол тек біреу ғана болатындығы шығады. Санның логарифмінің анықтамасынан аb саны сол шешім екендігі бірден табылады.
1-м ы с а л.
Теңдеуді шешейік
Берілген теңдеуді х-тің
+ 4х + 3 =
теңдігі орындалатындай мәндері ғана қанағаттандырады. Сонымен,
+ 4х + 5 = 0
квадрат теңдеу шықты. Оның түбірлері: 1 мен - 5 сандары. Олай болса, берілген теңдеудің шешімі екі сан, олар: 1 мен - 5.
2-м ы с а л.
Теңдеуді шешейік
Бұл теңдеу х-тің тек
2х + 3 > 0 және х + 1 > 0
теңсіздіктер орындалатындай мәндерінде ғана анықталады. х-тің мәндері үшін берілген теңдеу
2х + 3 = х+1
теңдеуімен мәндес. Бұдан х = - 2 екенін табамыз. Ал х = -2 саны х+1 > 0 теңсіздігін қанағаттандырмайды. Олай болса, берілген теңдеудің түбірлері болмайды.
Ал осы теңдеуді басқаша шешуге болар еді. Берілген теңдеудің салдарына
2х + 3 = х + 1
ауысып, х = - 2 екенін табамыз. Теңдеулерді мәндестік бұзылмайтындай етіп түрлендірген жағдайда, табылған мәнді бастапқы теңдеуге қойып, тексеру қажет.
Тап осы жағдайда
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz