Алгебралық теңдеулерді шешудің жолдарын тәжірибе мен теория жүзінде тиімділігін тексеру

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 22 бет
Таңдаулыға:

Мазмұны

Кіріспе . . . 2

1. Алгебралық теңсіздіктерді дәлелдеу . . . 3

2. Теңсіздіктерді дәлелдеу

2. 1 Қарапайым теңсіздіктерді дәлелдеу . . . 5

2. 2 Штурм әдісін қолданып теңсіздікті дәлелдеу . . . 6

3. Алгебралық теңсіздіктерді дәлелдеу әдістері.

3. 1 Теңсіздік ұғымының анықтамасын пайдаланып дәлелдеу . . . 7

3. 2 Теңсіздікті оның мүшелерін жуықтап бағалау тәсілімен дәлелдеу . . . 9

3. 3 Теңсіздіктерді аналитикалық тәсілмен дәлелдеу . . . 10

3. 4 Теңсіздіктерді синтетикалық тәсілмен дәлелдеу . . . 12

3. 5 Теңсіздіктердің дұрыстығын математикалық индукция әдісімен
дәлелдеу . . . 13

3. 6 Теңсіздіктердің дұрыстығын қарсы жору әдісімен дәлелдеу . . . 14

3. 7 Қиындығы жоғары теңсіздіктерді дәлелдеуге туындыны қолдану . . . 15

4. Арифметикалық, геометриялық, квадраттық, гармониялық орталардың ара қатынасын қолдану әдісі . . . 16

Қорытынды . . . 19

Пайдаланылған әдебиеттер тізімі . . . 20

Кіріспе

Тақырыптың өзектілігі: Теңдуелерді зерттеу, жуық есептеу, иррационал сандар теориясы, сан қатарлары т. б. теңсіздіктер қасиетіне сүйенеді. Жоғарғы мектептегі математикалық анализ курсында функциялардың максимум және минимум яғни экстримал есептерді шешуде теңсіздіктер кең түрде қолданылады.
Тек математикада ғана емес әр түрлі жаратылыстану ғылымдарында зерттелетін табиғаттың үздіксіз процестері әсіресе экологиялық, экономикалық т. б. халық шаруашылығындағы балайланыстар теңсіздіктің көмегімен шешіледі. Теңсіздіктер оқушыларды айқын және дұрыс ойлауға, шамаларды салыстыра білуге дағдыландырады.
Әр түрлі теңсіздіктер ерте заманда-ақ белгілі болған. Эвклит пен Архимед шығармаларында көптеген теңсіздіктер келтірілген. Осы күнгі теңсіздіктер таңбасы ХVІІІ ғасырда ағылшын ғалымы Томас Гариаттың латын тілінде жазылған «Аналитикалық өнердің практикасы атты еңбегінде» тұнғыш рет келтіріледі. Теңдіктер теңсіздіктен жасалады, оларды теңсіздіктердің дербес бір түрі деуге болады. Теңсіздікті теңдікке айналдыру үшін екі шаманың айырмасын дәл бағалау керек. Теңсіздіктер жай санды теңсіздіктер, алгебралық теңсіздіктер, классикалық теңсіздіктер болып бөлінеді. Теңсіздікті дәлелдегенде және шешкенде тек әріптер мен белгісіз шамалардың мүмкін мәндерін үнемі есепке алу керек. Мысалы: таңбасы белгісіздің мүмкін мәндерінің кейбіреуінде ғана сақталатын теңсіздікті шартты немесе белгісізі бар теңсіздік деп атайды. барлық теңсіздіктердің қасиеттерін тек санды теңсіздіктер арқылы көрсетуге болады.

Курстық жұмыстың құрлымы: Зерттеу жұмысы кіріспеден, төрт бөлімнен, қорытындыдан, пайдаланылған әдебиеттер тізімінен тұрады.

Зерттеудің мақсаты: білім беру сатылары арасындағы орта буынды оқушыларға алгебралық теңдеулерді шешудің жолдарын тәжірибе мен теория жүзінде тиімділігін тексеру. Оқушылардың білім іскерлік дағды, сапасын арттыру. Осындай білім алу нәтижесінде оқушылардың ақыл-ойын дамыту. Оқушылардың ғылыми дүниетанымын қалыптастыру, яғни эститикалық тәрбие беру. Қарапайым теңеулерді шешуде өмірлік-практикада пәнді оқып үйренуге пайдалана білу, шәкірттерді озбетінше білім алуын қамтамасыз ету және ғылыми әдістемелік негізін жасау.

Зеріттеу әдістері: нақтылы мәліметтер мен әдебиеттерге жүйелі талдау, баяндау, сипаттау, тұжырымдарды жинақтау, қорыту.

Жаңашылдығы: Оқушылардың ойлау еркіндігінің дамуы мен белсенділігінің артуына негізделеді. Оның басты мақсаты-сынып Оқушыларын «қабілетті», «қабілетсіз» деген жіктерге бөлуді болдырмау. Болашақта оқыту мен тәрбиелеу, әлеуметтік талап-тілектерді ескере отырып дамыту, ғылыми жетістіктер мен педагогикалық тәжірибелерді жаңартуға, мұғалімдерді ақпаратпен қамту, біліктілігін үздіксіз көтеруді қажет етеді.

1. Алгебралық теңсіздіктерді дәлелдеу

Өзара құрамында мына белгілердің ħ (үлкен), ≥ (үлкен не тең; кіші емес) (кіші), ≤ (кіші не тең, артық емес), ≠ 0 (тең емес) біреуі бар екі өрнекті (санды) теңсіздіктер деп атайды.

Екі жағы да бірдей алгебралық өрнектер болып келетін теңсіздіктерді алгебралық ьеңсіздіктер деп атайды.

Теңдуелерді зерттеу, жуық есептеу, иррационал сандар теориясы, сан қатарлары т. б. теңсіздіктер қасиетіне сүйенеді. Жоғарғы мектептегі математикалық анализ курсында функциялардың максимум және минимум яғни экстримал есептерді шешуде теңсіздіктер кең түрде қолданылады.

Тек математикада ғана емес әр түрлі жаратылыстану ғылымдарында зерттелетін табиғаттың үздіксіз процестері әсіресе экологиялық, экономикалық т. б. халық шаруашылығындағы балайланыстар теңсіздіктің көмегімен шешіледі. Теңсіздіктер оқушыларды айқын және дұрыс ойлауға, шамаларды салыстыра білуге дағдыландырады.

Әр түрлі теңсіздіктер ерте заманда-ақ белгілі болған. Эвклит пен Архимед шығармаларында көптеген теңсіздіктер келтірілген. Осы күнгі теңсіздіктер таңбасы ХVІІІ ғасырда ағылшын ғалымы Томас Гариаттың латын тілінде жазылған «Аналитикалық өнердің практикасы атты еңбегінде» тұнғыш рет келтіріледі. Теңдіктер теңсіздіктен жасалады, оларды теңсіздіктердің дербес бір түрі деуге болады. Теңсіздікті теңдікке айналдыру үшін екі шаманың айырмасын дәл бағалау керек. Теңсіздіктер жай санды теңсіздіктер, алгебралық теңсіздіктер, классикалық теңсіздіктер болып бөлінеді. Теңсіздікті дәлелдегенде және шешкенде тек әріптер мен белгісіз шамалардың мүмкін мәндерін үнемі есепке алу керек. Мысалы: таңбасы белгісіздің мүмкін мәндерінің кейбіреуінде ғана сақталатын теңсіздікті шартты немесе белгісізі бар теңсіздік деп атайды. барлық теңсіздіктердің қасиеттерін тек санды теңсіздіктер арқылы көрсетуге болады

1. а<b теңсіздігінен b>a теңсіздігі туады

2. а<b және b<c теңсіздіктерінен а<c теңсіздігі шығады

Бұл қасиет теңсіздікті шешкенде, теоремалар дәлелдегенде теңсіздікті «күшейту» үшін қолданылады.

3. а<b болса а+с<b+c болады

Теңсіздікті шешкенде, кейде ықшамдау мақсатымен оның екі бөлігінеде немесе екі бөлігінен де бірдей санды қосады немесе шегереді.

4. а-с<b болса а< b+c

Бұл қасиет бойынша теңсіздік мүшелерінең таңбасын өзгерте отырып, бір бөлігінен екінші бөлігіне көшіруге болады.

5. а<b және с<d болса а+с<b+d болады.

Шарт бойынша а-b<0 және c-d<0. Екі теріс санның қосындысы да теріс.

Теңсіздіктің дәлелдеу жолының белгілі бір алгоритмін анықтау қиын. Бірақ оған қарамастан теңсіздікті қандайда бір айқын теңсіздікке түрлендіру жолы бар екенін айта кеткен жөн. Содан кейін айқын теңсіздікті логикалық талдау арқылы берілген теңсіздікті келтіруге болады.

Негізгі теңсіздіктер: 1. а+в ≥√ав, а≥0, в≥0

2. а + в ≥2, (а мен в-ның таңбасы бірдей) ;

в а

3. 1: 1 ( 1 + 1 ) ≤√ав, а>0, в>0,

2 а в

Гармониялық орта;

4. 2ав ≤√ав≤ а+в ;

а+в 2

׀а+в׀≤׀а׀+׀в׀тек а·в≥0 болғанда орындалады

Теңсіздіктің түрлері:

Кейбір теңсіздіктер белгілі бір сандардың шамаларының әр түрлі орташаларына тәуелді болады. Бұл шамалар Hn≤Gn≤An≤Qn

A _n - арифметикалық орташа

G _n - геометриялық орташа

Q _n - квадраттық орташа

H _n - гармониялық орташа

a1+a2+…. +an≥√a1a2……. . an

n

a ₁ a ₂ …a _n сандарының арифметикалық орташасы, олардың геометриялық орташасынан аз емес. Бұл теңсіздікті француз математигі О. Каши 1821 жылы жариялағаг болатын.

Гюйгенс теңсіздігі
Чебышев теңсіздігі
Коши - Буняковский теңсіздігі
Бернулли теңсіздігі
Гельдер теңсіздігі

2. Теңсіздіктерді дәлелдеу

2. 1. Қарапайым теңсіздіктерді дәлелдеу

Теңсіздіктерді дәлелдеу кезінде матема-тикалық индукция әдісін қолдануға болады. Математикалық индукция әдісін пайдаланып натурал сан немесе натурал санға байланысты ұғымдары бар математикалық негіздеуді қажет ететін сөйлемдер дәлелденеді. Теңбе-теңдік-терді дәлелдеуге, шектеулі қосындыларды есептеуге және теңсіздіктерді шешуге көптеген дәлелдеу жолымен көз жеткізуге болады. Мектеп көлемінде қарапайым теңсіздіктер дәлелденеді, сол теңсіздіктер арқылы күрделі теңсіздіктерде дәлелденеді.

№1 а ² + b ² ≥ 2ab.

Дәлелдеуі:

a ² + b ² - 2аb = (а - b) ² ≥ 0.

№2

$\sqrt{\frac{a^{2} + b^{2}}{2}} \geq \frac{a + b}{2}$

кез келген a және b үшін.

Дәлелдеуі:

Берілген теңсіздіктен 2ab $\leq a^{2} + b^{2}$ , біз мына теңсіздікті аламыз

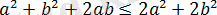
бұдан

$\frac{\ {(a + b) }^{2}}{4} \leq \frac{a^{2} + b^{2}}{2}$

Немесе

$\left( \frac{a + b}{2} \right) ^{2} \leq \frac{a^{2} + b^{2}}{2}$

соны мына түрде жазамыз

$\left \frac{a + b}{2} \right \leq \sqrt{\frac{a^{2} + b^{2}}{2}}$

бұдан

$\frac{a + b}{2} \leq \sqrt{\frac{a^{2} + b^{2}}{2}}$

2. 2. Штурм әдісін қолданып теңсіздікті дәлелдеу

Бұл әдісті неміс математигі Р. Штурм ұсынған. Бұл әдістің көмегімен бірнеше теңсіздікті дәлелдейік:

№3 Егер қосындысы 1-ге тең болса, онда 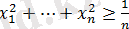дәлелдеу керек

Дәлелдеуі:

Егер

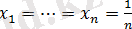
Онда

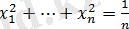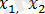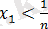
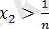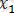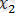Қаралатын сандардың ішінде ең болмағанда екі сан бір-біріне тең болмаса, онда сандардың ішінен екі сан табылады, сонын біреуі - нан үлкен болады, ал екіншісі кіші болады. Осы сандар болсын, және де болсын, онда - ді -ні 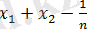- мен алмастырып, мынандай теңсіздік аламыз

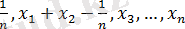
және олардың қосындысы 1-ге тең.

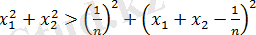
болғандықтан, осыдан

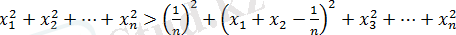Осы амалды бірнеше рет қайталап, шыққан тізбектің кез келген мүшесі -ге тең, ал олардың квадраттарының қосындысы берілген сандардың квадраттарының қосындысынан кіші болады.

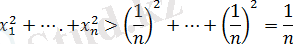
3. Алгебралық теңсіздіктерді дәлелдеу әдістері

3. 1. Теңсіздік ұғымының анықтамасын пайдаланып дәлелдеу.

Теңсіздіктің анықтамасы бойынша $\alpha$ ˃b болу үшін $\alpha$ -b˃0 болуы жеткілікті. Сондықтан $Α$ (х, у, . . . z) және $В$ (х, у, . . . z) алгебралық өрнектері үшін $Α$ (х, у, . . . z) ˃ $В$ (х, у, . . . z) екенін көрсету үшін х, у, . . . z айнымалылардың қарастырылып отырған жиыннан алынатын кез-келген сан мәндері үшін

$Α$ (х, у, . . . z) - $В$ (х, у, . . . z) ˃ 0 екенің дәлелдеу керек.

1-мысал.

Таңбалас кез келген екі нақты санның бір-біріне қатынастарының қосындысы 2-ден кем болмайтындығын, яғни $\alpha$ ·b ˃ 0 болса, онда

$\frac{\alpha}{b}$ + $\frac{b}{\alpha}$ ≥2 (1)

Дәлелденуі:Мына айырымды қарастырамыз

$\frac{\alpha}{b}$ + $\frac{b}{\alpha}$ -2= $\frac{\alpha 2 + b2 - 2\alpha b}{\alpha b}$ = $\frac{(\alpha - b) 2}{\alpha b}$

Бұл өрнек $\alpha \neq b$ болса оң, ал $\alpha = b$ болса нөлге тең. Сондықтан (1) дұрыс теңсіздік.

2 -мысал.

Екі он нақты санның арифметикалық ортасы, сол сандардың геометриялық ортасынан кем болмайды, яғни $\alpha ˃0, b˃0\$ болса, онда $\ \frac{\alpha + b}{2}$ ≥ $\ \sqrt{\alpha b}$ (2) болады (Коши теңсіздігі)

Дәлелдеуі:

Айырымын қарастырамыз.

$\frac{\alpha + b}{2}$ - $\sqrt{\alpha b}$ = $\frac{\ \alpha + b - 2\sqrt{\ \alpha b}}{2}$ = $\frac{(\sqrt{\ \alpha - \sqrt{\ b) }}}{2}$

Соңғы өрнек кез-келген $\alpha ˃0, b˃0\ сандары\ үшін\ оң, ал\ \alpha = b$ болса нөл. Сондықтан (2) теңсіздік дұрыс.

Берілген сандар жиынында қарастырылатын теңсіздіктің екі жағының да сандық сандық мағынасы болатын теңсіздіктің құрамына енетін әріптердің мүмкін мәндерін теңсіздіктің мүмкін мәндері деп аталады.

Мысал: Теңсіздіктің мүмкін мәндерін табыңдар.

$\frac{\ 2}{\ \alpha - 2}$ + $\frac{\ b}{\ \alpha + b}$ ˃ $\ \frac{1}{\ \alpha}$ +2 $\alpha\$ - $b$

Шешуі: Егер

$\left\{ \begin{array}{r} \ \alpha - 2 \neq 0 \\ \ \alpha + \ b \neq 0 \end{array} \right. \$

Яғни

$\left\{ \begin{array}{r} \ \alpha \neq 0 \\ \ \alpha \neq - b \end{array} \right. \$

болса, онда теңсіздіктің оң жағының мағынасы болады.

Жауабы: Теңсіздіктегі әріптердің мүмкін мәндері:

$\left\{ \ \begin{array}{r} \ \alpha \neq 0, \\ \ \alpha \neq 2 \\ \alpha \neq - b \end{array} \right. \$

Теңсіздіктің құрамына енетін әріптердің барлық мүмкін мәндерінде дұрыс болатын теңсіздіктерді теңбе-тең теңсіздіктер деп атайды.

2-мысал.

Оң сан үшін

$\alpha$ + $\frac{1}{\alpha}$ ≥2

болатындығын дәлелдендер.

Дәлелдеуі:

Айырымы

$\alpha\$ + $\frac{1}{\alpha}\$ - 2꞊ $\frac{\alpha 2 + 1 - 2\alpha}{\alpha}$ ꞊ $\frac{(\alpha - 1\ ) \ }{\alpha}$

Бұл кез келген $\alpha$ > 0 үшін оң сан. ондықтан теңсіздік дұрыс. Тепе-теңдік тек $\alpha ꞊1$

3. 2. Теңсіздікті оның мүшелерін жуықтап бағалау тәсілімен дәлелдеу

Бұл әдістікейде теңсіздікті «күшейту» немесе «бәсеңдету» әдісімен дәлелдеу деп те атайды. Бұл әдісте берілген теңсіздіктің мүшелерін жоғарыдан немесе төменнен бағалау арқылы дәлелдейді. Айталық бізге А˂В А˂В теңсіздігін дәлелдеу керек болсын. Сонда егер де біз А˂С А˂С және С˂В С˂В теңсіздіктерін дәлелдей алсақ онда теңсіздіктің транзитивті қасиеті бойынша А˂В А˂В теңсіздігі дәлелденген болып шығады. Бұл әдісті теңсіздікті «күшейту» әдісімен дәлелдеу деп атайды.

Мысал . Кез-келген натурал ⁿ саны үшін

1+ $\ \frac{1}{4}$ + $\frac{1}{9\ }$ + . . . + $\frac{1}{n2}$ ˂ $\frac{5}{3}$

теңсіздігі орындалатынын дәлелдендер.

Дәлелдеуі :

$\frac{1}{n2}$ ˂ $\frac{4}{4n2 - 1}$ =2 $\left( \binom{1}{2n - 1} - \binom{1}{2n + 1} \right)$

екені айқын. Сондықтан

S _n ˂1+2 $\left( \binom{1}{3} - \frac{1}{5} + \frac{1}{5} + \frac{1}{7} + \frac{1}{7} - \ \frac{1}{9} + \ldots + \frac{1}{2n - 1} - \frac{1}{2n + 1} \right)$ =

1+2 $\left( \binom{1}{3} - \frac{1}{2n + 1} \right)$ ˂1+ $\ \frac{2}{3}$ = $\frac{5}{3}$ ,

Олай болса

1+ $\frac{1}{4}$ + $\frac{1}{9}$ + $\frac{1}{n2}$ ˂ $\frac{5}{3}$

теңсіздігі ақиқат. Сонымен бірге теңсіздіктің дұрыстығы дәлелденді.

3. 3. Теңсіздіктерді аналитикалық тәсілмен дәлелдеу.

Теңсіздіктерді бұл тәсілмен дәлелдегенде берілген теңсіздікті дұрыс деп ұйғарып, теңсіздіктердің негізгі қасиеттеріне сүйене отырып, оны дұрыстығына күмән келтірмейтін түрге келтіреді. Одан кейін соңғы теңсіздіктен бастапқы берілген теңсіздікті шығарып алады. Енді осы тәсілге бірнеше мысалдар қарастырайық.

Мысал. Кез-келген оң α, b, c ˃0 сандары үшін

(α+b) ² ≤ (1+c) ·α ² +(1+ $\frac{1}{c}$ ) · b ²

теңсіздігінің орындалатындығын дәлелдендер.

Дәлелдеуі: Теңсіздікті дұрыс деп жорып, жақшаларды ашайық.

α ² +2αb+b ² ≤α ² +b ² +cα ² + $\frac{b2}{c}$ , 2αb≤ cα ²⁺ $\frac{b2}{c}$ $\Longrightarrow$ (α $\sqrt{c}$ - $\frac{b}{\sqrt{c}}$ ) ² ≥ 0

Бұл дұрыс теңсіздік. Олай болса, берілген теңсіздік те дұрыс. Сонымен берілген теңсіздіктің дұрыстығы дәлелденді.

2-мысал.

х ₁ ≥0, х ₂ ≥0, және х ₁₊ х ₂ ≤ $\ \frac{1}{2}$

болсын.

Мынаны дәлелдендер

(1-х ₁ ) ·(1-х ₂ ) ≥ $\frac{1}{2}$

Дәлелдеуі: Есептің шарты бойынша алатынымыз.

(1-х ₁ ) ·(1-х ₂ ) =1-(х ₁ +х ₂ ) ≥1 - $\frac{\ 1}{\ 2}$ = $\ \frac{1}{2}$

Сонымен берілген теңсіздіктің дұрыстығы дәлелденді. ·

3-мысал.

Теңсіздікті дәлелдендер:

$\alpha$ ² +b ² +1≥ $\ \alpha$ b+ $\ \alpha$ +b

Дәлелдеуі:

Дәлелденілуге тиісті теңсіздік оның екі жағын да бірдей 2-ге көбейкен соң мынадай түрде келеді.

2 $\alpha$ ² +2b ² +2 ≥ 2 $\ \alpha$ b+2 $\ \alpha$ + $\$ b,

немесе

$\alpha$ ² -2 $\ \alpha$ b + b ² + $\alpha$ ² -2 $\ \alpha$ ⁺¹⁺ $\$ b ² -2 $\$ b + 1 ≥0

немесе

( $\alpha$ -b) ² +( $\alpha$ -1) ² +(b-1) ² ≥ 0

Бұл теңдіктің орындалуы ақиқат

Теңдік белгісі тек $\alpha$ $꞊$ b ꞊ 1 болғанда ғана орындалады.

Сонымен берілген теңсіздіктің дұрыстығы дәлелденді. ·

4-мысал.

Айталық $\alpha$ , b, с-әртүрлі оң сандар болсын.

$\frac{\alpha\mathbf{\ } + b}{с}$ + $\frac{\alpha\mathbf{\ } + с}{b}$ + $\frac{b + с}{\alpha\mathbf{\ }\ }$ > 6

теңсіздігін тура болатындығын дәлелдендер.

Дәлелдеуі . Расында да берілген теңсіздікті былай жазуға болады.

$\left( \frac{\alpha\mathbf{\ }\ }{с} + \ \frac{с}{\alpha\mathbf{\ }\ } \right)$ + $\left( \frac{\alpha\mathbf{\ }\ }{b} + \frac{b}{\alpha\mathbf{\ }\ } \right)$ + $\left( \frac{b}{с} + \ \frac{с}{b} \right) \$ > 6

Соңында өзара кері екі оң санның қосындысы екіден артық болатындықтан, соңғы теңсіздіктің орындалатыны ақиқат.

Сонымен берілген теңсіздіктің дұрыстығы дәлелденді.

3. 4. Теңсіздіктерді синтетикалық тәсілмен дәлелдеу

Бұл тәсілді кейде тірек теңсіздіктер тәсілі деп те атайды. Бұл берілген теңсіздікті қандай да бар ақиқат теңсіздіктің немесе алдын ала дәлелденген теңсіздіктердің көмегі арқылы дәлелдеу тәсілі. Осындай көмекші теңсіздіктерді тірек теңсіздіктер деп атайды.

Мысалы:

α2≥0, α+b≥2 $\sqrt{\alpha b}$ , ( α≥0, b ≥0) $\frac{\alpha}{b}$ + $\frac{b}{\alpha}\$ ≥2, ( $\alpha b˃0)$

өрнектерін тірек теңсіздіктер ретінде қарастыруға болады.

Мысал: әрбір теріс емес α, b, c сандары үшін

(α+b) ·( α+c) ·( b+c) ≥8 αbc

теңсіздігі орындалатынын дәлелдендер.

Дәлелдеуі: Тірек теңсіздіктер ретінде

α+b≥2 $\sqrt{\alpha b\ }$ ; α+c≥2 $\sqrt{\alpha c\ }$ ; b+c≥2 $\sqrt{bc\ }$

теңсіздігін аламыз. Бұларды мүшелеп көбейту арқылы дәлелдеуге тиісті жоғарыдағы теңсіздікті шығарып аламыз:

(α+b) ·( α+c) ·( b+c) ≥2 $\sqrt{\alpha b\ }$ ·2 $\sqrt{\alpha c\ } \cdot$ 2 $\sqrt{bc\ }$ =8· $\sqrt{\alpha 2b2c2}$ =8 αbc

Сонымен берілген теңсіздіктің дұрыстығы дәлелденді.

2-мысал .

Теңсіздікті дәлелдеңдер:

$\frac{1}{\sqrt{1}}$ + $\frac{1}{\sqrt{2}}$ + $\frac{1}{\sqrt{3}}$ + . . . + $\frac{1}{\sqrt{1968}}$ > $\sqrt{1968}$

Дәлелдеуі:

1≤k≤1968

болсын, сонда

$\sqrt{\frac{1968}{k}}$ ≥1

Бұдан

$\sqrt{\frac{1968}{k1}}$ $+ \sqrt{\frac{1968}{2}}$ $+ \ldots + \sqrt{\frac{1968}{1968}}$ >1968

екені айқын. Осы теңсіздіктің екі жағы да бірдей $\sqrt{1968}$ -ге бөліп, дәлелденілуге тиіс теңсіздікті шығарып аламыз.

Сонымен берілген теңсіздіктің дұрыстығы дәлелденді .

3-мысал. Теңсіздікті дәлелдеңдер :

$\left( 1 + \frac{у}{х} \right)$ · $\left( 1 + \frac{z}{у} \right)$ · $\left( 1 + \frac{х}{z} \right) \geq$ 8,

мұндағы х > 0, у > 0, 𝑧 > 0.

Дәлелдеуі:

Кез келген α саны үшін α + $\frac{1}{\alpha}$ ≥ 0 екені белгілі.

Сондықтан

$\left( 1 + \frac{у}{х} \right)$ · $\left( 1 + \frac{z}{у} \right)$ · $\left( 1 + \frac{х}{z} \right) ꞊$ 1+ $\frac{z}{у}$ + $\frac{у}{х}$ + $\frac{z}{х}$ + $\frac{х}{z}$ + $\frac{х}{у}$ + $\frac{у}{z}$ +1꞊2+ $\left( \frac{у}{х} + \frac{х}{у} \right)$ + $\left( \frac{х}{z} + \frac{z}{х} \right)$ + $\left( \frac{у}{z} + \frac{z}{у}\ \right)$ ≥ 8

Сонымен берілген теңсіздіктің дұрыстығы дәлелденді .

3. 5. Теңсіздіктердің дұрыстығын математикалық индукция әдісімен
дәлелдеу

Математикалық индукция әдісінің негізінде мынадай қағида алынады: Қандай да бір пікір.

Натурал сан n=1 болғанда дұрыс болсын және

Бұл пікірдің кез-келген n=k(k≥1) мәні үшін дұрыстығынан, оның n=k+1 үшін де дұрыс болатындығы тағайындалса, онда ол пікір кез келген натурал сан n үшін дұрыс болады. Теңсіздіктің бір немесе екі жағы да бірдей натурал аргумент n-ге тәуелді болып келгенде теңсіздіктің дұрыстығын математикалық индукцияәдісін қолдану арқылы дәлелдеген тиімді. Теңсіздікті бұл әдіспен дәлелдегенде мына екі тұжырымды дәлелдейді.

А) n=1 үшін теңсіздіктің дұрыстығын оның n=k+1 үшін дұрыс болатындығы. Енді осы тәсілге мысал келтірейік:

Мысал:α≥ -1 болғанда кез келген натурал n саны үшін мына теңсіздіктің (1+α) ⁿ ≥1+nα орындалатындығын дәлелдендер.

Дәлелдеу: n=1 үшін теңсіздік дұрыс, өйткені 1+α≥1+α. Енді біз теңсіздіктің n=k натурал саны үшін дұрыс деп жорығанда (1+α) ^k ≥1+kα оның n=k+1 саны үшін дұрыс болатындығын, яғни (1+α) ^k+1 ≥1(k+1) α

Теңсіздігін орындалатынын көрсетейік. Ол үшін 2 теңсіздіктің екі жағы да бірдей 1+α˃0-ға көбейтеміз сонда kα ² ˃0 болатындықтан

(1+α) ^k+1 ≥(1+ kα) · (1+α) =1+(k+1) α+ kα ² $\Rightarrow$ (1+α) ^k+1 ≥1+(k+1) α болады. Сондықтан математикалық индукция әдісі бойынша 1 теңсіздік кез келген натурал ⁿ саны үшін дұрыс болады. Бұл теңсіздікті Бернулли теңсіздігі деп атайды. Сонымен теңсіздіктің дұрыстығы дәлелденді.

Мысал: Кез келген натурал ⁿ саны үшін $\sin{2ⁿ}$ α+ $\cos{2ⁿ}$ α≤1 теңсіздігінің орындалатынын дәлелдендер.