Тригонометриялық өрнектерді түрлендіру: теориясы, әдістері және теңдеулер жүйелерін шешу


Қазақстан Республикасының білім және ғылым министрлігі
М. Өтемісов атындағы Батыс Қазақстан мемлекеттік университеті
КУРСТЫҚ ЖҰМЫС
Тақырыбы:
«Тригонометриялық өрнектерді түрлендіру»
Орындаған: 04302 топ студенті Жардемов Н. А.
Тексерген: жаратылыстану ғылымдарының магистрі Маутеева С. М.
Орал, 2016ж.
Мазмұны
Кіріспе . . . 3
1. Тригонометриялық функциялар теориясы
1. 1 Кейбір тригонометриялық функциялар . . . 5
1. 2 Тригонометрия курсының әліппесі . . . 9
2. Тригонометриялық өрнектерді түрлендіру
2. 1 Тригонометриялық өрнектерді түрлендіру . . . 15
2. 2 Тригонометриялық теңдеулер жүйесін шешу . . . 19
Қорытынды . . . 21
Пайдаланылған әдебиеттер тізімі . . . 22
Кіріспе
Тақырып өзектілігі: Математиканың әр қадамы өмірдің қажетінен туады, сабақта қарастыратын көп есептер адамның практикалық дүниесіне байланысты. Сондықтан математикалық ұғымдардың нақты және тиімді болуы оқушылардың жеке тәрбиесіне байланысты, оқу жүйесіне қойыфлаын бірінші шарт - ол оқушылардың оқу процесі өмірімен байланысты болуы. Математикадан алған білім, біліктерін оқушылар тек еңбек және оқу әрекеттерінде қолданып қоймай, сонымен қатар мәдениеттің басқа салаларын да меңгертуге де пайдалануға болады. Математиканың тәрбиелік әсер етуі - оқушылардың бойында ой - өрісті, саналы ойлай білу ерекшеліктерін, өмірге деген көзқарастарын, танымдық ерекшеліктерін, патриоттылық сезімдерін оята отырып дамыту, қалыптастыруда үлкен роль атқарады. Ал, ондай жетістіктерге алгебралық материалдарды жетік меңгеру арқылы жеткізу мүмкін .
Тригонометрия (грек. trіgōnon - үшбұрыш және metreo - өлшеу) - геометрияның үшбұрыш элементтерінің арасындағы метрикалық қатыс тригонометриялық функциялар арқылы өрнектелетін саласы.
Тақырып мақсаты: Тригонометрияның негізгі мәселесі үшбұрыштың белгісіз шамаларын берілген шамалар арқылы есептеу болып табылады. Тригонометрия жазық, түзу сызықты және сфералық Тригонометрия болып бөлінеді. Евклидтік кеңістіктің сфералары қарастырылатын Тригонометрия сфералық тригонометрия деп аталады. Жазық Тригонометрия сфералық Тригонометриядан кейінірек дами бастады. Мысалы, Евклидтің «Негіздерінің» 2-кітабында косинустар теоремасы жайында айтылған. Тригонометрияны әл-Баттани (9-10 ғасырлар), Әбу-л-Вефа (10 ғасыр), Бхаскара (10 ғасыр) және ат-Туси (13 ғасыр), т. б. одан әрі дамытты. Оларға синустар теоремасы белгілі болған. Тангенстер теоремасын Региомонтан (15 ғасыр) тапқан. Одан кейін Тригонометрияны дамытуға Н. Коперник (16 ғасырдың 1-жартысы), Т. Браге (16 ғасырдың 2-жартысы), Ф. Виет (16 ғасыр), И. Кеплер (16-17 ғасырлар), т. б. үлес қосты. Қазіргі түріндегі Т. Л. Эйлердің еңбектерінде баяндалды.
Тригонометрия ғылыми термин ретінде адамның практикалық әрекеттерінің нәтижесінде пайда болды. Ерте кезде астрономия ғылымы, суда жүзу, жер өлшеу, архитектура талаптары қандай да бір элементтер арқылы есептеу әдістерін ойлап табуға әкелді. Мысалы, олардың көмегімен қол жетпейтін заттарға дейінгі қашықтықты анықтау және географиялық карталарды құрастыруға арналған жергілікті жердің геодезиялық көшірмесін жасау жұмыстары бірқатар оңайлатылды.
1. Тригонометриялық функциялар теориясы
1. 1 Кейбір тригонометриялық функциялар
Мектепте тригонометриялық материалмен алғаш рет планиметрия курсын оқығанда танысады. Тригонометрияның көмегімен жазық үшбұрыштарды шығарды. Тригонометриялық қатынастар «синус», «тангенс» деген атқа ие болды, олардың мәндері есептеліп шығарылды. Тригонометриялық танымдардың негізі ежелгі заманда пайда болды. Аталмасы біршама кейінірек шыққанымен тригонометрияға қатысты қазіргі көптеген ұғымдар мен фактілер бұдан екі мың жыл бұрын белгілі болған. Кейбір тригонометриялық мәліметтер ежелгі вавилондықтар мен египеттіктерге белгілі болған, бірақ ғылым ретінде Ежелгі Грецияда негізделген. Тригонометрия сөзі алғаш рет 1505 жылы неміс геологы және математигі Питискустың кітабының мазмұнында кездеседі. «Тригонометрия» атауының өзі грек сөзінен аударғанда «үшбұрыштарды өлшеу» деген ұғымды білдіреді. Ежелгі грек ғалымы белгілі астроном Клавдий Птолемей (ІІ ғ) «хорда тригонометриясын» ойлап тапты. Дайын кестелермен жұмыс істегенде немесе калькуляторды пайдаланғанда, біз көбінесе кестелер әлі ойлап табылмаған кездердің де болғанын естен шығарып аламыз. Оларды құру үшін аса көлемді есептеулерді орындап қана қоймай, кестелерді құрудың тәсілдерін де ойлап табу қажет болды. Птолемей кестесі бес ондық үлес таңбаларын қоса алғандағы дәлдікпен жасалған. Хордаларды синустармен ауыстырып, тригонометрияның әрі қарай дамуына Үндістандық ғалымдар үлкен үлес қосты. Бұл жаңа енгізі0у VIII ғасырда тригонометрияны бірте-бірте астрономия тарауынан бөліп алып, жеке ғылымға айналдырды. Ол араб тіліндегі жақын және алыс Батыс мемлекеттерінің математикасына ауысты. Оған үлес қосқандар Аль-хорезми, Аль-Коши, Насриддин Тусси, Жан фурье, Иоганн Бернули, Леонард Эйлер. Л. Эйлер тригонометрияның қазіргі кездегі түріне келтірілген XVIII ғасырдың ірі математигі еді, ол негізі швейцарлық, ұзақ жылдар бойы Россияда жұмыс істеген және Санкт-Петербург ғылым академиясының мүшесі болған. Тригонометриялық функциялардың белгілі анықтамасын да енгізген Л. Эйлер, кез келген бұрыштың функциясын қарастырып, келтіру формулаларын шығарып алды. Осылайша тригонометрия туралы жалпы ұғымдар, тригонометриялық функциялардың белгілеулері және анықтамалары ұзақ тарихи даму процесінде қалыптасып отыр.
Бірлік шеңбердегі Ө бұрышына қатысты тригонометриялық функциялар.
Бастапқы кезден тригонометриялық функциялартік бұрышты үшбұрыштағы қабырғаларының қатынастарымен байланыста болғаны белгілі. Олардың жалғыз аргументі сол үшбұрыштың бір сүйір бұрышы болып табылады.
Синус - қарама-қарсы жатқан катеттіңгипотенузаға қатынасы.
Косинус - жанама катеттің гипотенузағақатынасы.
Тангенс - қарама-қарсы жатқан катеттіңжанама катетке қатынасы.
Котангенс - жанама катеттің қарама-қарсы жатқан катетке қатынасы.
Секанс - гипотенузаның жанама катетке қатынасы.
Косеканс - гипотенузаның қарама-қарсы жатқан катетке қатынасы.
Берілген анықтамалар функциялардың сүйір бұрыштарға (0-ден
 радиан) қатысты мендерін есептеуге арналған.
радиан) қатысты мендерін есептеуге арналған.
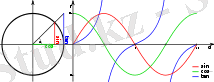
Тригонометриялық функциялардың графиктері.
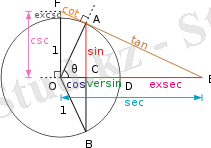
Бірлік шеңбердегі Ө бұрышына қатысты тригонометриялық функцияларды қарастырсақ (суретті қара) :
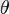 бұрышының Синусы "A" нүктесініңординатасы ретінде анықталады.
бұрышының Синусы "A" нүктесініңординатасы ретінде анықталады.
Косинус - "A" нүктесінің абсциссасы.
Тангенс - синустың косинусқа қатынасы.
Котангенс - косинустың синусқа қатынасы.
Секанс - косинуска кері өлшем.
Косеканс - синуска кері өлшем.
Тригонометриялық теңдеулер мен теңсіздіктерді шешу теңдеулер мен теңсіздіктердің басқа түрлерін шешуден бірінші кезекте оларды шешу нәтижесінде шешімдердің ақырсыз сериясын алуымызбен ерекшеленеді. Сондықтан осы теңдеулер мен теңсіздіктерді шешу нәтижелерін келтірумен шектелеміз. Негізгі тригонометриялық теңдеулер мыналар:
1)
Егер
болса, онда теңдеудің шешімдері жоқ.
Егер функциялардың графиктерін пайдалансақ, онда берілген теңдеудің шешуін көрнекі түрде аламыз.
теңдеуін графиктік шешуді
пен
функциялары графиктерінің қиылысу нүктелерінің абсциссаларын табу ретінде қарастыруға болады. Дәл осы теңдеуді графиктік әдіспен басқаша, тригонометриялық деп аталатын шеңберде, шешуге болады. Ол үшін радиусы бірге тең шеңбер сызамызда, оның центрі арқылы өзара перпендикуляр екі координаталар осьтерін жүргіземіз. Сондықтан біз жоғарыда келтірілген шешімдердің екі сериясын аламыз.
2)
Егер ׀а׀›1 болса, теңдеудің шешімдері жоқ.
формуласымен анықталатын айнымалының мәндерінің екі ақырсыз жиыны болады.
3)
Кез келген а үшін оның шешімдері
формуласымен беріледі.
4)
Кез келген а үшін оның шешімдері
формуласымен беріледі.
Негізгі емес тригонометриялық теңдеулерді немесе теңсіздіктерді шешу бір немесе бірнеш негізгі тригонометриялық теңдеулерді немесе теңсіздіктерді шешуге келтіріледі. Негізгі емес теңдеулер мен теңсіздіктерді негізгілерге келтіру процесі тригонометриялық функцияларды тепе-тең түрлендірулердің формулалары арқылы әр түрлі түрлендірулердің көмегімен, сондай-ақ айнымалыларды ауыстырудың және көбейткіштерге жіктеудің көмегімен жүргізіледі.
1. 2 Тригонометрия курсының әліппесі
Өркениет жолындағы адамзат тіршілігі, яғни құрылыс салу істері тригонометрияның пайда болуына әкелді.
Жаратылысты зерттеу, аспан шырақтарының біздің тіршілігімізге тигізетін әсерлерін анықтау бағытындағы ғылыми жұмыстар тригонометрия курсының тереңдеп қалыптасуына жол ашты. Әлемдегі барлық тіршілік, қозғалыс құбылыстары айналым, цикл, дөңгелек арқылы сипатталады. Сондықтан да декарттық координаталар жазықтығындағы тригонометриялық шеңбер немесе бірлік шеңбер табиғи заңдылықтарды бейнелеудің математикадағы мысалы болып табылады.
Сүйір бұрыштың (0 0 -тан 90 0 -қа дейінгі) тригонометриялық функциялары синус, косинус, тангенс, котангенстерді анықтау үшін тік бұрышты АВС үшбұрышын қарастырайық:

Осыған сәйкес:
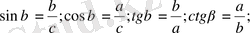
Синус пен косинус, тангенс пен котангенс өзара кофункциялар деп аталады.
Қарапайым осы анықтаулардың өзінен алдағы тригонометриядағы едәуір күрделі есептерді ұтымды шығаруға мүмкіндік беретін мына теңдіктерді еске ұстау маңызды: егер,
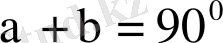 болса,
болса,
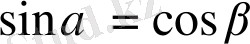
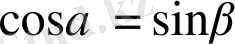
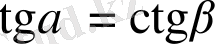
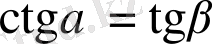 болады. Қысқашалап жазсақ, функция(α) =кофункция(β), егер,
болады. Қысқашалап жазсақ, функция(α) =кофункция(β), егер,
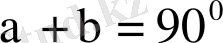 .
.
Мысалдар:
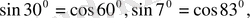
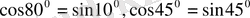
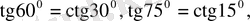
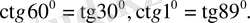
Әрі қарай өзіміздің бес саусағымыздай білуімізге тиісті мәселе: 0 0 , 30 0 , 45 0 , 60 0 , 90 0 -тық бұрыштардың (бір қызығы, бұлардың саны да бесеу) синусының мәндері.
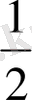
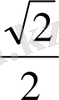
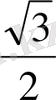
Кей оқушыларға бұл кестені жаттау оңай, кейбірі үстірт қараудың салдарынан «синус 300-та неше болады?», «синус 450 -та неше болады?» тәрізді сұрақтарға ойланып қалса, көпшілігі қате жауапты айта салады. Тригонометриялық есептерді дұрыс шығаруды үйренуге ниеттенген болсаңыз, бірнеше жол жоғарыда орналасқан кестедегі синустың мәндеріне тағы да назар аударыңыз!
Енді бұл мәндерді еске ұстаудың бір тәсілін үйренелік: бөлімінде тұрақты 2-саны, ал, алымында
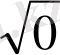 ,
,
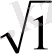 ,
,
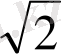 ,
,
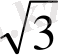 ,
,
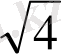 сандары орналасқан бес бөлшекті жадымызға түю анағұрлым жеңіл болатыны сөзсіз.
сандары орналасқан бес бөлшекті жадымызға түю анағұрлым жеңіл болатыны сөзсіз.
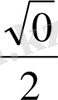
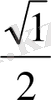
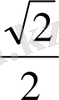
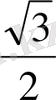
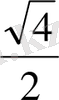
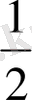
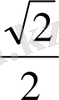
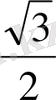
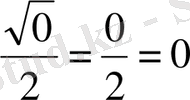 ,
,
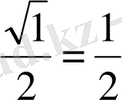 ,
,
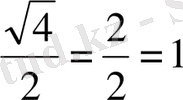 болатынын оқушымыз өзі де біледі деп сенемін. Ал,
болатынын оқушымыз өзі де біледі деп сенемін. Ал,
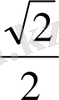 ,
,
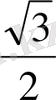 мәндерін әрі қарай ықшамдаудың қажеті жоқ.
мәндерін әрі қарай ықшамдаудың қажеті жоқ.
0 0 , 30 0 , 45 0 , 60 0 , 90 0 -тық бұрыштардың қалған тригонометриялық функцияларының (косинус, тангенс, котангенс) мәндерін синустың мәндеріне байланыстыра жаттауға болады.
Синустың жоғарыдағы бес мәнін кері ретпен жазу арқылы косинустың мәндері алынады.
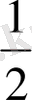
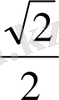
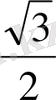
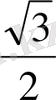
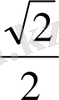
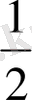
, , ,
теңдіктерін сіз білесіз. Себебі, бұл теңдіктердің екі жағында өзара кофункциялар орналасқан және олардың бұрыштарының қосындысы 900-қа тең.
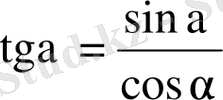 теңдігін пайдалансақ,
тангенстің мәндері алынады.
теңдігін пайдалансақ,
тангенстің мәндері алынады.
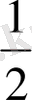
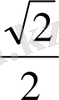
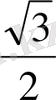
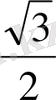
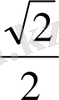
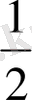
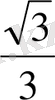
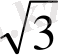
Әрине, ол үшін мынадай қарапайым есептеулерді орындау қажет:
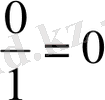 ,
,
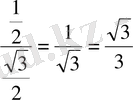 ,
,
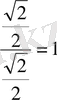 ,
,
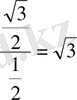 ,
,
 -бөлшегінің мәні жоқ (санды 0-ге бөлуге болмайды) !
-бөлшегінің мәні жоқ (санды 0-ге бөлуге болмайды) !
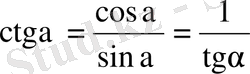 немесе
немесе
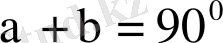 жағдайы үшін
жағдайы үшін
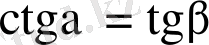 теңдіктерінің кез-келгенін пайдаланып, немесе жай ғана тангенстің кестедеге мәндерін кері ретпен жазып шығу арқылы
котангенстің мәндері алынады.
теңдіктерінің кез-келгенін пайдаланып, немесе жай ғана тангенстің кестедеге мәндерін кері ретпен жазып шығу арқылы
котангенстің мәндері алынады.
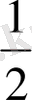
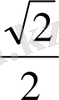
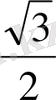
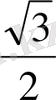
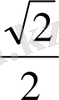
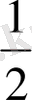
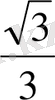
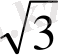
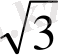
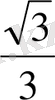
Тригонометриялық фигуралардың қасиеттері.
2. Тригонометриялық өрнектерді түрлендіру
2. 1 Тригонометриялық өрнектерді түрлендіру
Тригонометриялық үйлесімдіктер - ортақ анықталу облысындағы барлық аргументтері үшін орындалатын тригонометриялық функциялардың математикалық өрнектері.
Тригонометриялық теңдеулерді шығарғанда әртүрлі тәсілдерді пайдаланып, түрлендіріп, қарапайым теңдеулерге келтіреді.
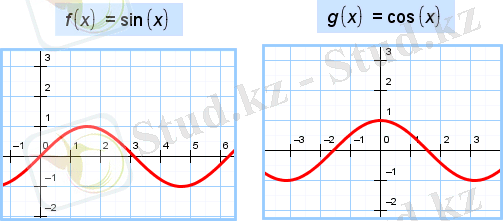
Функцияның:
- Анықталу облысы:
2. Мәндер жиыны
sinx - тақ, cosx- жұп. Ең кіші оң периоды
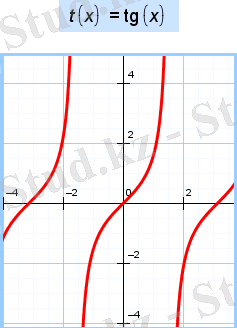
Функцияның:
1. Анықталу облысы: ,
,
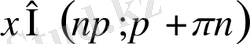
2. Мәндер жиыны
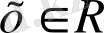
3.
- тақ., ең кіші оң периоды
 .
.
Квадрат теңдеуге келтіріп шығарылатын теңдеулер.
1-мысал:

Шешуі:
cosx = t алмастырамыз, сонда
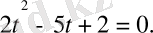

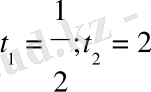

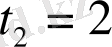 алынбайды,
алынбайды,
себебі
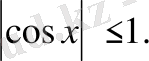 ендеше
ендеше
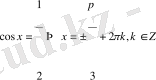
2-мысал
.
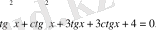
Шешуі
:
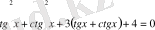
tgx+ctgx =y деп белгілейміз. Сонда
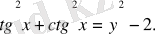

Біртекті тригонометриялық теңдеулер.
Анықтама
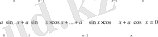
Түріндегі теңдеулерді sinx және cosx -ке қатысты n-ші дәрежелі біртекті тригонометриялық теңдеу дейді, мұндағы
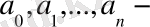 нақты сандар,
нақты сандар,
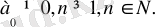
Барлық қосылғыштарда sinx және cosx-тің дәреже көрсеткіштерінің қосындысы n-ге тең.
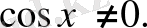 деп екі жағында бөліп,
деп екі жағында бөліп,
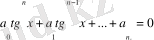
түрінде теңдеу аламыз.
1-мысал
.
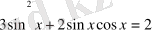 Шешуі:
Шешуі:

2-мысал
.
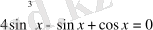
Шешуі
:
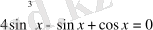 түрлендірейік:
түрлендірейік:
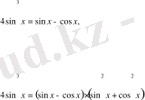

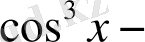 ке екі жағын бөлеміз.
ке екі жағын бөлеміз.
Сонда:
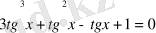
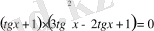

Дәрежені төмендету арқылы шығаратын теңдеулер.
3-Мысал.
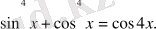
Шешуі
:
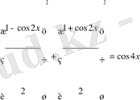
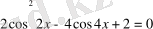
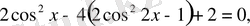
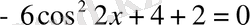 ,
,
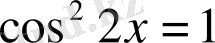
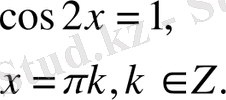
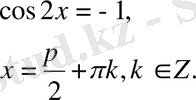
Қосымша бұрыш енгізу тәсілі.
4-Мысал
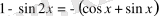
Шешуі:
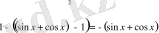
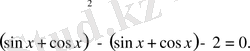
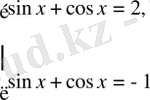
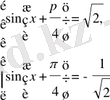
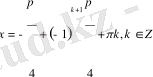
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz